分式复习(精品公开课)名师制作优质教学资料
- 格式:ppt
- 大小:640.50 KB
- 文档页数:23




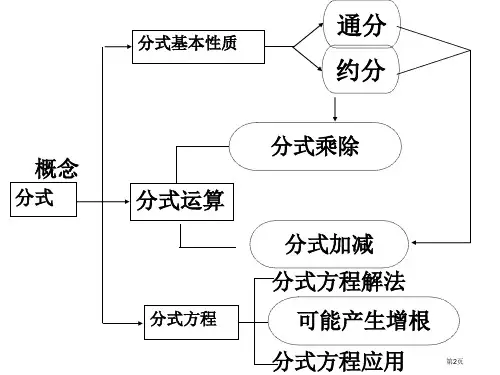

胶州市公开课 教学案 授课时间 2016-5-27胶州市第二十五中学八年级数学下册主备人_ _ 复备人_ 审核_张其 授课班级 八年级_ 课型 复习课_ 课题:第五章 分式复习一 一、【教学目标】知识与技能: (1)使学生进一步熟悉分式的意义及分式的运算;(2)提高学生分式的基本运算技能.数学能力:(1)提高学生的运算能力,发展学生的合情推理能力;二、【教学重点和难点 】学习重点:1.分式的基本性质 2.分式的运算学习难点 分式的四则运算----它是整式运算、因式分解和分式运算的综合三、基础知识复习:★知识点一: 分式的概念:整式A 除以整式B ,可以表示成 的形式,如果除式B 中含有 ,那么称 为分式.其中A 称为分式的分子,B 称为分式的分母。
★知识点二:分式有关的条件:①若 ,则分式有意义;②若 ,则分式无意义;③若 ,则分式的值 =0.◆小练习一:1.在代数式中,分式共有_____个 213124, , , (), , 32232m x x a b x y x π---+-2、当x 时,分式x-13有意义。
3、分式)3)(1(12---x x x 有意义的条件是____ _____。
值为零的条件是4.当x 时,分式 242--x x 无意义。
5、若分式1-x x 无意义,则x= 。
★知识点三:分式的基本性质:分式的分子与分母都乘以(或除以)分式的 .用式子表示为 .★知识点四:1.约分:把一个分式的分子和分母的 约去,这种变形称为分式的约分.约分的依据是2.约分的结果是:_________ ___3.约分时要注意:(1)要找出分子分母的公因式;(2)分子、分母是多项式的要先分解因式再约分; (3)约分要彻底。
★知识点五:最简分式 :分子与分母中不含___ ___的分式◆小练习二:1、下列分式中是最简分式的是( )12.2+x x A x B 24. 11.2--x x C 11.--x x D2.化简下列分式:abd bca 81412)( 164)2(22--x x x 22164)3(m m m --想一想:如何进行约分?约分的技巧:1.如果分式的分子、分母都是单项式,先找出分子和分母的__ ______,然后直接约去。


《分式复习》教案教案编写者:教案编辑专员教学目标:1. 理解分式的概念,掌握分式的基本性质。
2. 掌握分式的运算规则,包括加减乘除。
3. 能够解决实际问题,运用分式进行合理计算。
教学重点:1. 分式的概念和基本性质。
2. 分式的运算规则。
3. 分式在实际问题中的应用。
教学难点:1. 分式的运算规则的理解和运用。
2. 解决实际问题时分式的合理运用。
教学准备:1. 教学PPT或者黑板。
2. 教学素材和实例。
教学过程:第一章:分式的概念与基本性质1.1 分式的概念教学内容:介绍分式的定义,解释分子和分母的概念。
教学方法:通过PPT展示分式的定义,引导学生理解分子和分母的关系。
教学活动:1. 向学生介绍分式的定义,解释分子和分母的概念。
2. 通过PPT展示分式的图形表示,帮助学生直观理解分式的含义。
3. 引导学生进行小组讨论,分享对分式的理解。
教学评估:通过小组讨论和学生的提问,了解学生对分式的理解程度。
1.2 分式的基本性质教学内容:介绍分式的基本性质,包括分式的符号规则、分式的乘法和除法。
教学方法:通过PPT展示分式的基本性质,引导学生进行实例分析和练习。
教学活动:1. 向学生介绍分式的基本性质,包括分式的符号规则、分式的乘法和除法。
2. 通过PPT展示分式的基本性质的实例,引导学生进行分析和练习。
3. 组织学生进行小组讨论,分享对分式基本性质的理解和运用。
教学评估:通过小组讨论和学生的提问,了解学生对分式的基本性质的理解程度。
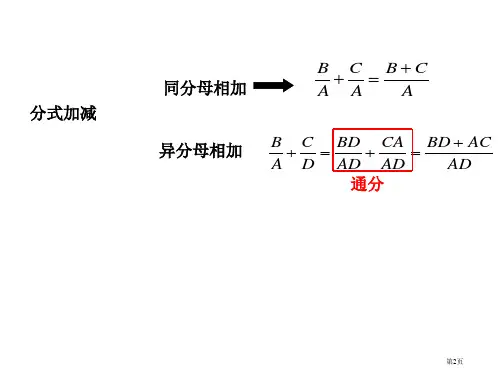
第二章:分式的运算规则2.1 分式的加减法教学内容:介绍分式的加减法规则,解释同分母和异分母的分式加减法。
教学方法:通过PPT展示分式的加减法规则,引导学生进行实例分析和练习。
教学活动:1. 向学生介绍分式的加减法规则,解释同分母和异分母的分式加减法。
2. 通过PPT展示分式的加减法实例,引导学生进行分析和练习。
3. 组织学生进行小组讨论,分享对分式加减法的理解和运用。
教学评估:通过小组讨论和学生的提问,了解学生对分式的加减法的理解程度。

《分式方程》复习课教学设计教材分析分式方程是初中数学的重点内容,本节课是北师大版八年级下册第五章《分式与分式方程》第四节—分式方程的复习课,分式方程的核心是转化与应用,发展学生的化归意识,体会模型思想,本节主要复习分式方程的解法与增根问题,解分式方程的关键把分式方程转化为整式方程,同时对增根问题进行适当拓展延伸.教学目标进一步掌握分式方程的定义、解法、增根;通过展示、交流、质疑等方式促进学生对知识的掌握,体会数学的转化思想,发展运算能力和化归意识.重点和难点重点:进一步理解分式方程的定义、掌握分式方程的解法,渗透解题的基本方法与思想. 难点:进一步理解和解决增根的有关的问题.教学策略⑴学法:通过展示,交流,质疑、总结等方式促进学生对分式方程相关知识的理解与掌握,渗透数学解题的思想与方法.⑵教法:采用了引导式、探究式教学法,结合导学案以练习为平台,学生为主体,教师为主导的思路贯穿整个课堂.过程与方法一、定义跟踪下列关于x 的方程中,是分式方程的是 (只填序号). ①3423+=-x x ②xx 321=- ③0322=--x x ④22121--=--x x x ⑤1222=---x x x m ⑥1317-=+-x ax x 【设计意图】这一环节的设计,考察学生对基础知识的掌握,不是简单的让学生重复定义,而是通过展示一组方程让学生进行辨别,在此过程中学生必将调动自己对分式方程定义的理解,同时还要注意区分分式方程与整式方程, ⑤、⑥中辅助字母的设计又帮助学生理解分式方程定义的关键点——分母中含有未知数,所以本设计可以说是站在较高的层次上对分式方程定义的理解.二、巩固练习①x x 321=- ②22121--=--xx x 【设计意图】因为解分式方程是要求学生掌握的基本技能,所以先让学生通过独立解题,回顾解分式方程的一般步骤,然后结合解题过程中出现的问题,明白解题过程中的注意点,反思解题中常出现的错误,从正、反两个方面加深学生对知识的理解和掌握.三、拓展延伸⑴若关于x 的分式方程1222=---xx x m 出现增根,则m = . ⑵若关于x 的分式方程1222=---x x x m 的解为正数,则m 的取值范围是 . 【设计意图】解分式方程是基本的计算题题型之一,用途很广很重要,引入不同的题型,变式类似的题型,使学生更进一步掌握分式方程的解法及增根,发展学生计算能力和化归意识.四、当堂检测1.解下列分式方程: ①x x 413=- ②14143=-+--xx x 2. 若关于x 的分式方程211=+-x k 的解为负数,则k 的取值范围是 . 【设计意图】让学生独立完成,通过这两道题的解答,一方面,检测学生掌握情况,以便老师在后续的教学中做到心中有数、因材施教;另一方面,让学生更好好的理解增根,从而突破本节课的难点,达到复习的预期效果.五、课后思考若关于x 的分式方程1317-=+-x ax x 无解,则a = . 【设计意图】由于分式方程的无解问题是学生理解上的难点,学生通过本节课的学习可能还会存在疑惑,因此安排了课后思考这一环节让学生自主探究,所选题是在理解增根基础上的灵活应用,能够帮助学生较好的理解分式方程无解问题,并能根据已有的知识将其解决.1.本节课借助导学案,课堂以问题的形式设计本节的相关知识,通过基础练习促进了学生对知识的掌握,提高学生的运算能力和化归意识;通过逐渐递进的练习,突出重点,分散难点,较好的达到复习巩固的目的,这样的程序符合学生的认知规律,使不同的学生得到了不同的发展和提高2.学生学习过程中,进一步渗透了转化的数学思想,因为分式方程的核心是转化与应用,发展学生的化归意识,体会模型思想,本节主要复习分式方程的解法与增根问题,解分式方程的关键把分式方程转化为整式方程,同时对增根问题进行适当拓展延伸.。