简谐振动的运动学描述

简谐运动的描述引言简谐运动是物理学中一种重要的运动形式，它在自然界和工程领域中都有广泛的应用。

本文将对简谐运动进行详细描述，并深入探讨其特征、数学表达以及应用。

定义简谐运动是一种周期性运动，其特点是运动体沿着某个轴线上往复振动，并且振动的加速度与位移成正比，且恒定。

在简谐运动中，运动体会围绕平衡位置作周期性的振动，如弹簧振子、摆锤等。

特征简谐运动有以下几个主要特征：1.振幅（Amplitude）：振幅是指运动体离开平衡位置的最大位移。

它决定了简谐运动的最大振幅。

2.周期（Period）：周期是指运动体完成一次完整振动所需的时间。

它与频率的倒数成正比，可以用公式T = 1/f来表示，其中T代表周期，f代表频率。

3.频率（Frequency）：频率是指运动体单位时间内振动的次数。

它与周期的倒数成正比，可以用公式f = 1/T来表示，其中f代表频率，T代表周期。

4.相位（Phase）：相位是指简谐运动的偏移值，用角度来度量。

在简谐运动中，相位角随时间而变化，可以用公式θ = ωt来表示，其中θ代表相位角，ω代表角频率，t代表时间。

5.动能和势能：在简谐运动中，运动体会交替转化为动能和势能。

当运动体离开平衡位置时，具有最大位移和最大动能；当运动体接近平衡位置时，具有最小位移和最小动能，但具有最大势能。

数学表达简谐运动的数学表达可以通过以下公式得到：1.位移（Displacement）：\[x(t) = A \cos(\omega t + \phi)\] 其中，x代表位移，A代表振幅，ω代表角频率（ω = 2πf），t代表时间，φ代表相位角。

2.速度（Velocity）：\[v(t) = -A \omega \sin(\omega t + \phi)\] 其中，v代表速度，A代表振幅，ω代表角频率（ω = 2πf），t代表时间，φ代表相位角。

3.加速度（Acceleration）：\[a(t) = -A \omega^2 \cos(\omega t + \phi)\] 其中，a代表加速度，A代表振幅，ω代表角频率（ω = 2πf），t代表时间，φ代表相位角。

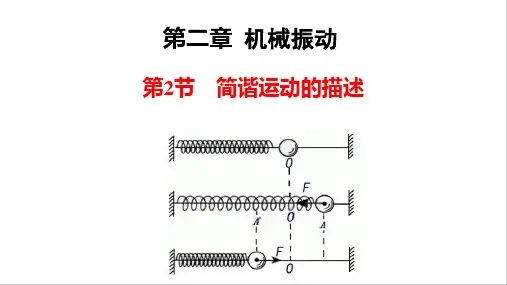
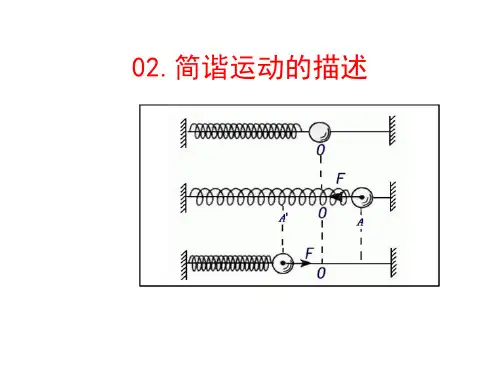
简谐运动的描述一、简谐运动的概念和特征简谐运动是一种重要的周期性运动，它可以在自然界和人-made系统中观察到。

简谐运动的特征包括：1.周期性：简谐运动是一个重复的过程，物体会在规律的时间间隔内重复相同的运动。

2.能量守恒：简谐运动中物体的总能量保持不变，由动能和势能相互转化，但总能量始终保持恒定。

3.线性回复：简谐运动中，物体的回复力与它的偏离程度成正比，且方向相反，符合胡克定律。

4.最大回复力和最大速度的时刻不一致：简谐运动中，最大回复力与最大速度不会同时发生，它们的时刻相差1/4个周期。

二、简谐运动的数学描述简谐运动可以使用如下的数学描述：一维简谐运动的位移-时间关系：x=Acos(ωt+ϕ)其中， - A为振幅，表示物体偏离平衡位置的最大距离。

- ω为角频率，表示单位时间内的相位变化量。

- t为时间。

- φ为初相位，表示在t=0时刻的位相。

一维简谐运动的速度-时间关系：v=−ωAsin(ωt+ϕ)一维简谐运动的加速度-时间关系：a=−ω2Acos(ωt+ϕ)三、简谐运动的力学模型简谐运动可以通过一维弹簧振子来进行力学建模。

弹簧振子由一个弹簧和一个质量块组成。

当质量块受到外力扰动后，它会围绕平衡位置做简谐振动。

1.弹簧的自由长度为L，当质量块偏离平衡位置时，弹簧受到回复力，使得质量块回到平衡位置。

2.弹簧回复力与质量块的偏离程度成正比，符合胡克定律：F=−kx其中， - F为回复力的大小。

- k为弹簧的劲度系数，描述了弹簧的刚度和回复力的大小。

- x为质量块偏离平衡位置的距离。

四、简谐运动的频率和周期简谐运动的频率和周期和与力学模型中的角频率相关。

频率：简谐运动的频率表示单位时间内完成一个完整周期的次数，用hertz（Hz）作为单位，频率等于角频率除以2π。

周期：简谐运动的周期表示完成一个完整周期所需要的时间，用秒（s）作为单位，周期等于角频率的倒数。

五、简谐运动的实际应用简谐运动是自然界和人-made系统中普遍存在的一种运动形式，其应用十分广泛。

简谐振动的规律和特点简谐振动是一种重要的物理现象，它在自然界和人类生活中都有广泛的应用。

本文将详细介绍简谐振动的规律和特点，并从多个角度进行描述。

一、简谐振动的规律和特点1. 定义：简谐振动是指物体在一个平衡位置附近做往复振动的运动。

它的运动方式具有周期性和对称性，是一种非常规律的振动。

2. 弹簧振子的例子：弹簧振子是最常见的简谐振动的例子之一。

当弹簧振子受到外力拉伸或压缩后，当外力移除时，它会以平衡位置为中心作往复振动。

3. 动力学规律：简谐振动的运动规律可以由胡克定律和牛顿第二定律得出。

根据胡克定律，当弹性体受力时，其恢复力与位移成正比。

牛顿第二定律则表明物体的加速度与作用力成正比，与质量成反比。

结合这两个定律，可以推导出简谐振动的运动方程。

4. 运动方程：简谐振动的运动方程可以表示为x = A * sin(ωt + φ)，其中x是物体的位移，A是振幅，ω是角频率，t是时间，φ是相位差。

这个运动方程描述了物体在平衡位置两侧往复振动的过程。

5. 特点一：周期性。

简谐振动的最基本特点是其运动是周期性的，即物体在一个周期内重复完成相同的运动。

周期T是指物体完成一个完整振动所需的时间，与角频率ω的倒数成正比。

6. 特点二：振幅和频率。

简谐振动的振幅A表示物体在振动过程中最大的位移，频率f表示单位时间内完成的振动次数。

振幅和频率都是简谐振动的重要参数，它们与物体的质量、劲度系数、外力等因素有关。

7. 特点三：相位差和初相位。

相位差是指两个简谐振动之间的时间差，初相位是指物体在某一时刻的位移相对于平衡位置的位置。

相位差和初相位对于描述简谐振动的运动状态和相互作用非常重要。

8. 特点四：能量转化。

简谐振动是一种能量在不同形式之间转化的过程。

在振动过程中，物体的动能和势能会不断相互转化，当物体通过平衡位置时，动能最大，而位移最大时，势能最大。

9. 特点五：应用广泛。

简谐振动的规律和特点在物理学、工程学、生物学等领域都有广泛的应用。

运动学中的圆周运动与简谐振动运动学是物理学中研究物体运动状态、运动规律的分支学科。

在运动学中，圆周运动和简谐振动是两个常见的运动形式。

本文将探讨圆周运动和简谐振动在运动学中的特性和应用。

一、圆周运动在物理学中，圆周运动指物体在一个平面上沿着一条圆弧运动的情形。

而当物体在进行圆周运动时，它受到向心力的作用。

向心力的大小与物体的质量和速度的平方成正比，与运动的半径成反比。

圆周运动的速度可以用线速度或角速度来描述。

1.1 线速度和角速度线速度是指物体在圆周上运动的速度，可以表示为物体在圆周上运动的路程除以所花费的时间。

在圆周运动中，线速度的大小与物体沿圆周弧长所运动的距离和所花费的时间成正比。

如果用v表示线速度，l表示弧长，t表示所花费的时间，那么线速度v可以表示为v=l/t。

角速度是指物体在圆周运动中所占据的角度的变化速率。

通常用小写希腊字母ω来表示角速度，单位为弧度/秒。

角速度可以用角度或弧度来表示，其中1弧度=180°/π。

1.2 向心力和向心加速度在圆周运动中，物体受到向心力的作用。

向心力的大小与物体的质量和线速度的平方成正比，与圆周运动的半径成反比。

向心力的方向与物体运动方向垂直，指向圆心。

根据牛顿第二定律，向心力可以表示为F=mv²/r，其中F表示向心力，m表示物体的质量，v表示物体的线速度，r表示圆周运动的半径。

通过对向心力的分析，可以获得物体的向心加速度。

1.3 圆周运动的应用圆周运动在日常生活和工程领域中有广泛的应用。

例如，摩天轮、行星绕太阳的运动、地球的自转等都属于圆周运动。

工程上的一些设备，如离心机、离心泵等也利用了圆周运动的原理。

二、简谐振动简谐振动是指一个物体在受力驱动下沿着固定轨道来回振动的运动。

简谐振动具有周期性和重复性，其运动规律可以用正弦或余弦函数来描述。

简谐振动是一个重要的物理现象，广泛应用于科学领域和工程实践中。

2.1 简谐振动的特性简谐振动具有以下特性：- 振动物体在平衡位置附近往复振动；- 振幅是振动物体距离平衡位置最大偏离的距离；- 周期是振动物体完成一次往复振动所需要的时间；- 频率是振动物体完成一个周期所需要的次数。

简谐运动的描述简谐运动的描述简谐运动是指一个物体在一个恒定的力场中做周期性的振动。

它是一种特殊的振动，具有周期性、稳定性和可预测性等特点。

简谐运动在自然界和工业生产中都有广泛应用，如弹簧振子、钟摆、电磁波等。

一、简谐运动的基本概念1.1 振幅振幅是指简谐运动中物体从平衡位置最大偏离距离。

通常用字母A表示，单位为米（m）。

1.2 周期周期是指简谐运动中物体完成一次完整振动所需要的时间。

通常用字母T表示，单位为秒（s）。

1.3 频率频率是指单位时间内完成的振动次数。

通常用字母f表示，单位为赫兹（Hz）。

1.4 相位相位是指在同一时刻内处于不同状态的两个物体之间的时间差。

相位差可以用角度来表示，通常用字母Φ表示。

二、简谐运动的数学描述2.1 速度与加速度公式对于简谐运动而言，速度和加速度分别可以用以下公式来计算：v = Aωcos(ωt + Φ)a = -Aω^2sin(ωt + Φ)其中，ω为角速度，可以用以下公式计算：ω = 2πf2.2 位移公式对于简谐运动而言，物体的位移可以用以下公式来计算：x = Acos(ωt + Φ)其中，A为振幅，Φ为相位差。

三、简谐运动的特点3.1 周期性简谐运动具有周期性，即物体在恒定的力场中做周期性的振动。

物体完成一次完整振动所需要的时间是固定的。

3.2 稳定性简谐运动具有稳定性，即物体在恒定的力场中做周期性的振动时，其运动状态是稳定并可预测的。

3.3 可预测性由于简谐运动具有稳定性和周期性，因此可以精确地预测物体在未来某一时刻所处的位置、速度和加速度等状态。

四、简谐运动的应用4.1 弹簧振子弹簧振子是一种常见的简谐振动系统。

它由一个质量和一个弹簧组成，在重力作用下进行周期性振动。

弹簧振子广泛应用于工业生产中的测量和控制系统中。

4.2 钟摆钟摆是一种通过重力驱动的简谐振动系统。

它由一个重物和一个支架组成，在重力作用下进行周期性振动。

钟摆广泛应用于时间测量、科学研究和导航等领域。

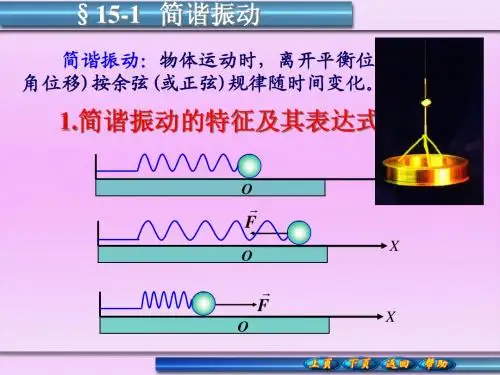
第十五章振动学基础§15-1简谐振动【基本内容】一、简谐振动的动力学描述1、谐振动的受力特征谐振动的动力学定义：振动系统在与位移大小成正比，而方向相反的回复力作用下的运动称为简谐振动。

kxf-=, k为比例系数。

2、简谐振动的微分方程222=+xdtxdωmk=ω3、简谐振动的判据判据一kxf-=动力学判据判据二运动学判据判据三)cos(φω+=tAx运动方程4、简谐振动实例单摆小角度摆动、复摆、扭摆二、简谐振动的运动学描述1、谐振动的数学表达式——运动方程谐振动的运动学定义：位移按余弦规律移随时间变化的运动是谐振动。

)cos(φω+=tAx)cos()sin(2φωωφωω+-=+-=tAatAv2、简谐振动的三个特征量角频率、频率、周期——由振动系统的性质决定。

角频率：mk=ω周期：ωπ2=T频率：T1=ν振幅A ——表示振动物体离开平衡位置的最大距离。

振幅A 和初相ϕ由初始条件决定：⎪⎪⎩⎪⎪⎨⎧-=+=-)(0012202x v tg v x A ωϕω 度ω（1（2（3（4123、谐振动的机械能：2222121ωmA kA E E E p K ==+=弹簧振子的动能和势能按正弦或余弦的平方随时间作周期性变化，其周期为谐振周期的一半；当动能最大时，势能最小；当动能最小时，势能最大；但机械能保持恒定不变。

【典型例题】【例15-1】半径为R 的木球静止浮于水面上时，其体积的一半浸于水中，求： （1）木球振动的微分方程；22222)31(dtxd m g R x x R =--ρπ平衡位置时：ρπ33421R m ⋅=，故 0)31(232222=-+Rx x R g dt x d 此即木球的运动微分方程。

当R x <<时，0322→R x02322=+x R gdtx d 木球作简谐振动g R T R g 3222,23πωπω===【例15-2】 弹簧下挂g m 1000=的法码时，弹簧伸长cm 8。

简谐振动的运动学方程简谐振动的运动学方程简谐振动是物理学中非常重要的一种振动形式，它广泛应用于机械、电子、光学等领域。

简谐振动的运动学方程是描述其运动规律的数学公式，本文将从以下几个方面详细介绍简谐振动及其运动学方程。

一、简谐振动的定义和特点1.1 简谐振动的定义简谐振动是指一个物体在弹性力作用下沿某一轴向做周期性往复运动的现象。

其中，弹性力是指当物体发生形变时所产生的恢复力，该力与形变量成正比例关系。

1.2 简谐振动的特点（1）周期性：简谐振动具有周期性，即一个完整的往复运动所需时间相等。

（2）等加速度：在整个周期内，物体所受加速度大小相等。

（3）最大速度和最大位移：在整个周期内，物体达到最大速度和最大位移时刻相同。

二、简谐振动的数学表达式2.1 位移函数对于一个做简谐运动的物体，在任意时刻t时其位置可以用位移函数x(t)表示。

假设物体在t=0时刻位于平衡位置，则位移函数可以表示为：x(t) = A cos(ωt + φ)其中，A表示振幅，即最大位移；ω表示角频率，即单位时间内振动的圆周角度；φ表示初相位。

2.2 速度函数对于一个做简谐运动的物体，在任意时刻t时其速度可以用速度函数v(t)表示。

速度函数可以通过对位移函数求导得到，即：v(t) = -Aω sin(ωt + φ)其中，负号表示速度方向与位移方向相反。

2.3 加速度函数对于一个做简谐运动的物体，在任意时刻t时其加速度可以用加速度函数a(t)表示。

加速度函数可以通过对速度函数求导得到，即：a(t) = -Aω^2 cos(ωt + φ)三、简谐振动的运动学方程3.1 运动学方程的定义运动学方程是描述物体在某一轴向上做运动规律的数学公式。

对于简谐振动而言，其运动学方程包括了物体的位置、速度和加速度三个方面。

3.2 简谐振动的运动学方程根据以上所述，我们可以得到简谐振动的运动学方程：x(t) = A cos(ωt + φ)v(t) = -Aω sin(ωt + φ)a(t) = -Aω^2 cos(ωt + φ)其中，x(t)表示物体在任意时刻t时的位移；v(t)表示物体在任意时刻t 时的速度；a(t)表示物体在任意时刻t时的加速度。

简谐振动的特点和动力学描述简谐振动是物体在恢复力作用下沿着某个轴线上做往复振动的一种特殊运动形式。

它具有以下几个特点：1. 平衡位置稳定：简谐振动的平衡位置是物体的稳定位置，当物体偏离平衡位置时，会受到一个恢复力的作用，使得物体趋向于返回平衡位置。

2. 振幅固定：简谐振动的振幅是一个固定值，表示物体在振动过程中离开平衡位置的最大距离。

3. 频率恒定：简谐振动的频率与振动系统本身的性质有关，而与振幅无关。

频率是指单位时间内振动的完整周期数，单位为赫兹（Hz）。

4. 正弦函数描述：简谐振动的运动可用正弦函数来描述。

物体在简谐振动过程中，其位置、速度和加速度随时间的变化都可以用正弦函数表示。

根据简谐振动的特点，在动力学上可以进行如下的描述：1. 动力学方程：对于简谐振动，其动力学方程可以由胡克定律得到。

胡克定律指出，弹性力与物体偏离平衡位置的距离成正比，即恢复力F 与位移x的关系为F = -kx，其中k为弹性系数。

2. 牛顿第二定律：根据牛顿第二定律，物体的加速度与作用力成正比，与物体的质量成反比。

对于简谐振动，可以将牛顿第二定律应用于沿轴线的振动，并根据动力学方程得到加速度与位移之间的关系。

3. 振动的能量：在简谐振动中，物体的能量在势能和动能之间不断转换。

当物体通过平衡位置时，其动能最大，而势能最小；当物体运动到最大位移时，其势能最大，而动能最小。

总能量保持不变。

4. 平衡位置的稳定性：简谐振动的平衡位置是稳定的，当物体偏离平衡位置时，会受到恢复力使其回到平衡位置。

这种稳定性是由弹簧的弹性恢复力所决定的。

综上所述，简谐振动具有稳定平衡位置、固定振幅、恒定频率等特点，并可以通过动力学方程和能量转换进行描述和分析。

研究简谐振动有助于理解振动现象的基本规律，对于很多领域如机械、电子、光学等都有重要的应用价值。