第三章 三角恒等变换章末复习
- 格式:docx
- 大小:225.00 KB
- 文档页数:8
![三角恒等变换 章末复习课 Word版含答案 ]](https://img.taocdn.com/s1/m/48e08f4bb4daa58da1114a2d.png)
题型一 灵活变角的思想在三角恒等变换中的应用给值求值的重要思想是沟通已知式与待求式之间的联系,常常在进行角的变换时,要注意各角之间的和、差、倍、半的关系,如α=2·α2,α=(α+β)-β,α=β-(β-α),α=12[(α+β)+(α-β)],β=12[(α+β)-(α-β)]等. 例1 已知α、β为锐角,cos α=45,tan(α-β)=-13,求cos β的值. 解 ∵α是锐角,cos α=45,∴sin α=35,tan α=34. ∴tan β=tan [α-(α-β)]=tan α-tan (α-β)1+tan αtan (α-β)=139. ∵β是锐角,故cos β=91050. 跟踪训练1 已知tan(α-β)=12,tan β=-17,且α,β∈(0,π),求2α-β的值. 解 tan α=tan [(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β=13>0. 而α∈(0,π),故α∈(0,π2). ∵tan β=-17,0<β<π,∴π2<β<π. ∴-π<α-β<0.而tan(α-β)=12>0, ∴-π<α-β<-π2. ∴2α-β=α+(α-β)∈(-π,0).∵tan(2α-β)=tan [α+(α-β)]=tan α+tan (α-β)1-tan αtan (α-β)=1,∴2α-β=-3π4. 题型二 整体换元的思想在三角恒等变换中的应用在三角恒等变换中,有时可以把一个代数式整体视为一个“元”来参与计算和推理,这个“元”可以明确地设出来(如例2令sin x -cos x =t ).例2 求函数y =sin x +sin 2x -cos x (x ∈R )的值域.解 令sin x -cos x =t ,则由t =2sin ⎝⎛⎭⎫x -π4知t ∈[-2,2], 又sin 2x =1-(sin x -cos x )2=1-t 2.∴y =(sin x -cos x )+sin 2x =t +1-t 2=-⎝⎛⎭⎫t -122+54. 当t =12时,y max =54; 当t =-2时,y min =-2-1.∴函数的值域为⎣⎡⎦⎤-2-1,54. 跟踪训练2 求函数f (x )=sin x +cos x +sin x ·cos x ,x ∈R 的最值及取到最值时x 的值. 解 设sin x +cos x =t ,则t =sin x +cos x =2⎝⎛⎭⎫22sin x +22cos x =2sin ⎝⎛⎭⎫x +π4, ∴t ∈[-2,2],∴sin x ·cos x =(sin x +cos x )2-12=t 2-12. ∴f (x )=sin x +cos x +sin x ·cos x即g (t )=t +t 2-12=12(t +1)2-1,t ∈[-2,2]. 当t =-1,即sin x +cos x =-1时,f (x )min =-1.此时,由sin ⎝⎛⎭⎫x +π4=-22, 解得x =2k π-π或x =2k π-π2,k ∈Z . 当t =2,即sin x +cos x =2时,f (x )max =2+12. 此时,由2sin ⎝⎛⎭⎫x +π4=2,sin ⎝⎛⎭⎫x +π4=1. 解得x =2k π+π4,k ∈Z . 综上,当x =2k π-π或x =2k π-π2,k ∈Z 时,f (x )取得最小值,f (x )min =-1;当x =2k π+π4,k ∈Z 时,f (x )取得最大值,f (x )max =2+12. 题型三 转化与化归的思想在三角恒等变换中的应用三角函数式的化简就是通过恒等变换化繁为简.其中切化弦、异名化同名、异角化同角等方法均为转化与化归思想的运用;三角恒等式的证明就是消除等式两边的差异,有目的的化繁为简,左右归一或变更论证,也属转化与化归思想的应用.例3 求证:tan 32x -tan x 2=2sin x cos x +cos 2x .证明 ∵左边=tan 32x -tan x 2=sin 32x cos 32x -sin x 2cos x 2=sin 32x cos x 2-sin x 2cos 32x cos x 2cos 32x =sin x12(cos 2x +cos x )=2sin x cos x +cos 2x =右边.∴tan 32x -tan x 2=2sin x cos x +cos 2x. 跟踪训练3 已知cos ⎝⎛⎭⎫π4+x =35,17π12<x <7π4,求sin 2x +2sin 2x 1-tan x的值. 解 sin 2x +2sin 2x 1-tan x =sin 2x +2sin 2x cos x cos x 1+tan x=sin 2x (1+tan x )1-tan x=sin 2x ·tan ⎝⎛⎭⎫π4+x .∵17π12<x <7π4,∴5π3<x +π4<2π, 又∵cos ⎝⎛⎭⎫π4+x =35,∴sin ⎝⎛⎭⎫π4+x =-45. ∴tan ⎝⎛⎭⎫π4+x =-43. ∴cos x =cos ⎣⎡⎦⎤⎝⎛⎭⎫π4+x -π4 =cos ⎝⎛⎭⎫π4+x cos π4+sin ⎝⎛⎭⎫π4+x sin π4 =22×⎝⎛⎭⎫35-45=-210. ∴sin x =sin ⎣⎡⎦⎤⎝⎛⎭⎫π4+x -π4 =sin ⎝⎛⎭⎫π4+x cos π4-sin π4cos ⎝⎛⎭⎫π4+x =-7210, sin 2x =725.∴sin 2x +2sin 2x 1-tan x=-2875. 题型四 构建方程(组)的思想在三角恒等变换中的应用方程(组)思想是中学重要的思想方法之一.借助三角函数公式构建关于某些量的方程(组)来求解,也是三角求值中常用的方法之一.例4 已知锐角三角形ABC 中,sin(A +B )=35,sin(A -B )=15. (1)求证:tan A =2tan B .(2)设AB =3,求AB 边上的高.(1)证明 ∵sin(A +B )=35,sin(A -B )=15, ∴⎩⎨⎧ sin A cos B +cos A sin B =35,sin A cos B -cos A sin B =15⇒⎩⎨⎧ sin A cos B =25,cos A sin B =15⇒tan A tan B=2. ∴tan A =2tan B . (2)解 ∵π2<A +B <π,sin(A +B )=35, ∴tan(A +B )=-34,即tan A +tan B 1-tan A tan B=-34. 将tan A =2tan B 代入上式并整理得2tan 2B -4tan B -1=0,解得tan B =2±62,舍去负值,得tan B =2+62. ∴tan A =2tan B =2+ 6.设AB 边上的高为CD ,则AB =AD +DB =CD tan A +CD tan B =3CD 2+6, 由AB =3,得CD =2+ 6.∴AB 边上的高等于2+ 6.跟踪训练4 已知向量m =(cos θ,sin θ)和n =(2-sin θ,cos θ),θ∈(π,2π),且|m +n |=825,求cos ⎝⎛⎭⎫θ2+π8 的值.解 m +n =(cos θ-sin θ+2,cos θ+sin θ),|m +n |=(cos θ-sin θ+2)2+(cos θ+sin θ)2=4+22(cos θ-sin θ)= 4+4cos ⎝⎛⎭⎫θ+π4 =2 1+cos ⎝⎛⎭⎫θ+π4. 由已知|m +n |=825,得cos ⎝⎛⎭⎫θ+π4=725. 又cos ⎝⎛⎭⎫θ+π4=2cos 2⎝⎛⎭⎫θ2+π8-1, 所以cos 2⎝⎛⎭⎫θ2+π8=1625.∵π<θ<2π,∴5π8<θ2+π8<9π8. ∴cos ⎝⎛⎭⎫θ2+π8<0.∴cos ⎝⎛⎭⎫θ2+π8=-45. [呈重点、现规律]本章所学的内容是重要的三角恒等变换,在三角式求值、化简、证明,进而研究三角函数的性质等方面都是必要的基础,是解答整个三角函数类试题的必要基本功,要求准确,快速化到最简,再进一步研究函数的性质.。




第三章 三角恒等变换一、知识点总结1、两角和与差的正弦、余弦和正切公式:⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-; ⑶()sin sin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+; ⑸()tan tan tan 1tan tan αβαβαβ--=+ ⇒ (()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan 1tan tan αβαβαβ++=- ⇒ (()()tan tan tan 1tan tan αβαβαβ+=+-).2、二倍角的正弦、余弦和正切公式:⑴sin22sin cos ααα=.222)cos (sin cos sin 2cos sin 2sin 1ααααααα±=±+=±⇒ ⑵2222cos2cossin 2cos 112sin ααααα=-=-=-⇒升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+⇒降幂公式2cos 21cos 2αα+=,21cos 2sin 2αα-=. ⑶22tan tan 21tan ααα=-. 3、⇒(后两个不用判断符号,更加好用)4、合一变形⇒把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的 B x A y ++=)sin(ϕϖ形式。
()sin cos αααϕA +B =+,其中tan ϕB=A. 5.(1)积化和差公式sin α·cos β=21[sin(α+β)+sin(α-β)] cos α·sin β=21[sin(α+β)-sin(α-β)] cos α·cos β=21[cos(α+β)+cos(α-β)] sin α·sin β= -21[cos(α+β)-cos(α-β)](2)和差化积公式 sin α+sin β=2cos2sin2βαβα-+sin α-sin β=2sin2cos2βαβα-+ααααααα半角公式cos 1cos 12tan 2cos 12sin ;2cos 12cos :+-±=-±=+±=2tan 12tan 1 cos ;2tan 12tan2sin :222αααααα万能公式+-=+=cos α+cos β=2cos2cos2βαβα-+ cos α-cos β= -2sin2sin2βαβα-+tan α+ cot α=ααα2sin 2cos sin 1=⋅ tan α- cot α= -2cot2α 1+cos α=2cos 22α 1-cos α=2sin22α1±sin α=(2cos2sinαα±)26。
第三章 三角恒等变换3.1两角和与差的正弦、余弦和正切公式⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-; ⑶()sin sin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+; ⑸()tan tan tan 1tan tan αβαβαβ--=+ ⇒ (()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan 1tan tan αβαβαβ++=- ⇒ (()()tan tan tan 1tan tan αβαβαβ+=+-).25、二倍角的正弦、余弦和正切公式:⑴sin 22sin cos ααα=.222)cos (sin cos sin 2cos sin 2sin 1ααααααα±=±+=±⇒ ⑵2222cos2cossin 2cos 112sin ααααα=-=-=-⇒升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+⇒降幂公式2cos 21cos 2αα+=,21cos 2sin 2αα-=. 26、22tan tan 21tan ααα=-. 27、⇒(后两个不用判断符号,更加好用) 28、合一变形⇒把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的 B x A y ++=)sin(ϕϖ形式。
)sin αϕA +B ,其中tan ϕB =A. 29、三角变换是运算化简的过程中运用较多的变换,提高三角变换能力,要学会创设条件,灵活运用三角公式,掌握运算,化简的方法和技能.常用的数学思想方法技巧如下:(1)角的变换:在三角化简,求值,证明中,表达式中往往出现较多的相异角,可根据角与角之间的和差,倍半,互补,互余的关系,运用角的变换,沟通条件与结论中角的差异,使问题获解,对角的变形如:①α2是α的二倍;α4是α2的二倍;α是2α的二倍;2α是4α的二倍; ②2304560304515o ooooo=-=-=;问:=12sin π ;=12cos π;③ββαα-+=)(;④)4(24αππαπ--=+;⑤)4()4()()(2απαπβαβαα--+=-++=;等等(2)函数名称变换:三角变形中,常常需要变函数名称为同名函数。
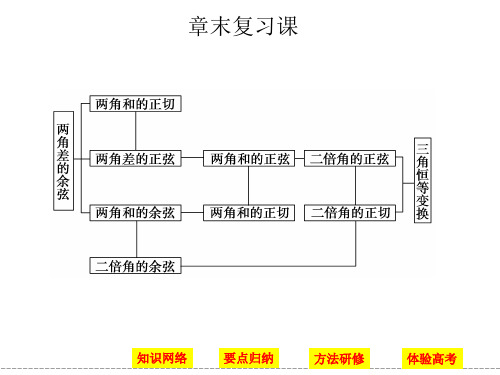
三角恒等变换章末复习一、网络构建二、要点归纳1.两角和与差的正弦、余弦、正切公式cos(α-β)=cos αcos β+sin αsin β.cos(α+β)=cos αcos β-sin αsin β.sin(α+β)=sin αcos β+cos αsin β.sin(α-β)=sin αcos β-cos αsin β.tan(α+β)=tan α+tan β1-tan αtan β.tan(α-β)=tan α-tan β1+tan αtan β. 2.二倍角公式sin 2α=2sin αcos α.cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α.tan 2α=2tan α1-tan 2α. 3.升幂缩角公式1+cos 2α=2cos 2α.1-cos 2α=2sin 2α.4.降幂扩角公式sin x cos x =sin 2x 2,cos 2x =1+cos 2x 2, sin 2x =1-cos 2x 2. 5.和、差角正切公式变形tan α+tan β=tan(α+β)(1-tan αtan β),tan α-tan β=tan(α-β)(1+tan αtan β).6.辅助角公式y =a sin ωx +b cos ωx =a 2+b 2sin(ωx +θ).⎝⎛⎭⎫其中tan θ=b a .题型一 三角函数求值例1 (1)sin 110°sin 20°cos 2155°-sin 2155°的值为( ) A .-12 B.12 C.32 D .-32考点 利用二倍角公式化简求值题点 利用正弦的二倍角公式化简求值答案 B解析 原式=sin 70°sin 20°cos 310°=cos 20°sin 20°cos 50°=12sin 40°sin 40°=12. (2)已知α,β为锐角,cos α=45,tan(α-β)=-13,求cos β的值. 考点 角的拆分与组合在三角恒等变换中的应用题点 角的拆分与组合在三角恒等变换中的应用解 ∵α是锐角,cos α=45, ∴sin α=35,tan α=34. ∴tan β=tan [α-(α-β)]=tan α-tan (α-β)1+tan αtan (α-β)=139. ∵β是锐角,故cos β=91050. 反思感悟 三角函数的求值问题通常包括三种类型,即给角求值,给值求值,给值求角.给角求值的关键是将要求角转化为特殊角的三角函数值;给值求值关键是找准要求角与已知角之间的联系,合理进行拆角、凑角;给值求角实质是给值求值,先求角的某一三角函数值,再确定角的范围,从而求出角.跟踪训练1 已知tan(α+β)=25,tan ⎝⎛⎭⎫β-π4=14,那么tan ⎝⎛⎭⎫α+π4等于( ) A.1318 B.1322 C.322 D.16考点 两角和与差的正切公式题点 利用两角和与差的正切公式求值答案 C解析 tan ⎝⎛⎭⎫α+π4=tan ⎣⎡⎦⎤(α+β)-⎝⎛⎭⎫β-π4=25-141+25×14=322. 题型二 三角函数式的化简与证明例2 化简:2cos 4x -2cos 2x +122tan ⎝⎛⎭⎫π4-x sin 2⎝⎛⎭⎫π4+x .考点 整体与换元思想在三角恒等变换中的应用题点 整体与换元思想在三角恒等变换中的应用解 原式=-2sin 2x cos 2x +122sin ⎝⎛⎭⎫π4-x cos 2⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x =12(1-sin 22x )2sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x =12cos 22x sin ⎝⎛⎭⎫π2-2x =12cos 2x . 反思感悟 三角函数化简常用策略有:切化弦、异名化同名、降幂公式、1的代换等,化简的结果应做到项数尽可能少,次数尽可能低,函数名尽量统一.三角函数证明常用方法有:从左向右(或从右向左),一般由繁向简;从两边向中间,左右归一法;作差证明,证明“左边-右边=0”;左右分子、分母交叉相乘,证明差值为0等.跟踪训练2 证明:sin α+11+sin α+cos α=12tan α2+12. 考点 三角恒等式的证明题点 三角恒等式的证明证明 ∵左边=2sin α2cos α2sin 2α2+cos 2α2+11+2sin α2cos α2sin 2α2+cos 2α2+cos 2α2-sin 2α2sin 2α2+cos 2α2=2tan α21+tan 2α2+11+2tan α21+tan 2 α2+1-tan 2α21+tan 2α2=tan 2α2+2tan α2+11+tan 2α2+2tan α2+1-tan 2α2=⎝⎛⎭⎫tan α2+122tan α2+2=12⎝⎛⎭⎫tan α2+1 =12tan α2+12=右边, ∴原等式成立.题型三 三角恒等变换与函数、向量的综合运用例3 已知向量a =(cos α,sin α),b =(cos β,sin β),|a -b |=255. (1)求cos(α-β)的值;(2)若-π2<β<0<α<π2,且sin β=-513,求sin α的值. 考点 和、差角公式的综合应用题点 和、差角公式与其他知识的综合应用解 (1)因为向量a =(cos α,sin α),b =(cos β,sin β),|a -b |=(cos α-cos β)2+(sin α-sin β)2=2-2cos (α-β)=255, 所以2-2cos(α-β)=45,所以cos(α-β)=35. (2)因为0<α<π2,-π2<β<0,所以0<α-β<π, 因为cos(α-β)=35, 所以sin(α-β)=45,且sin β=-513,cos β=1213, 所以sin α=sin [(α-β)+β]=sin(α-β)cos β+cos(α-β)·sin β=45×1213+35×⎝⎛⎭⎫-513=3365. 反思感悟 三角函数与三角恒等变换综合问题,通常是通过三角恒等变换,如降幂公式,辅助角公式对三角函数式进行化简,最终化为y =A sin(ωx +φ)+k 或y =A cos(ωx +φ)+k 的形式,再研究三角函数的性质.当问题以向量为载体时,一般是通过向量运算,将问题转化为三角函数形式,再运用三角恒等变换进行求解.跟踪训练3 已知函数f (x )=cos ⎝⎛⎭⎫2x +π3+sin 2x -cos 2x +23sin x cos x . (1)化简f (x );(2)若f (α)=17,2α是第一象限角,求sin 2α. 考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值解 (1)f (x )=12cos 2x -32sin 2x -cos 2x +3sin 2x =32sin 2x -12cos 2x =sin ⎝⎛⎭⎫2x -π6.(2)f (α)=sin ⎝⎛⎭⎫2α-π6=17,2α是第一象限角,即2k π<2α<π2+2k π(k ∈Z ),∴2k π-π6<2α-π6<π3+2k π(k ∈Z ),∴cos ⎝⎛⎭⎫2α-π6=437,∴sin 2α=sin ⎣⎡⎦⎤⎝⎛⎭⎫2α-π6+π6=sin ⎝⎛⎭⎫2α-π6·cos π6+cos ⎝⎛⎭⎫2α-π6·sin π6=17×32+437×12=5314.1.若α,β都是锐角,且cos α=55,sin(α-β)=1010,则cos β等于() A.22 B.210C.22或-210 D.22或210考点 和、差角公式的综合应用题点 综合运用和、差角公式化简求值答案 A解析 由α,β都是锐角,且cos α=55,sin(α-β)=1010,得sin α=255,cos(α-β)=31010,∴cos β=cos [α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=22. 2.若3sin x +cos x =4-m ,则实数m 的取值范围是( )A .[2,6]B .[-6,6]C .(2,6)D .[2,4]考点 简单的三角恒等变换的应用题点 辅助角公式与三角函数的综合应用答案 A解析 ∵3sin x +cos x =4-m ,∴32sin x +12cos x =4-m 2, ∴sin π3sin x +cos π3cos x =4-m 2,∴cos ⎝⎛⎭⎫x -π3=4-m 2. ∵⎪⎪⎪⎪cos ⎝⎛⎭⎫x -π3≤1,∴⎪⎪⎪⎪4-m 2≤1,∴2≤m ≤6. 3.在△ABC 中,若tan A tan B =tan A +tan B +1,则cos C 的值是( ) A .-22 B.22 C.12 D .-12考点 简单的三角恒等变换的应用题点 简单的三角恒等变换与三角形的综合应用答案 B解析 由tan A ·tan B =tan A +tan B +1,得tan A +tan B 1-tan A ·tan B=-1,即tan(A +B )=-1. ∵A +B ∈(0,π),∴A +B =3π4.∴C =π4,cos C =22. 4.化简:sin (180°+2α)1+cos 2α·cos 2αcos (90°+α)= . 考点 利用简单的三角恒等变换化简求值题点 综合运用三角恒等变换公式化简求值答案 cos α5.已知函数f (x )=cos x ·sin ⎝⎛⎭⎫x +π3-3cos 2x +34,x ∈R . (1)求f (x )的最小正周期;(2)求f (x )在闭区间⎣⎡⎦⎤-π4,π4上的最大值和最小值. 考点 简单的三角恒等变换的综合应用题点 简单的三角恒等变换与三角函数的综合应用解 (1)由已知,得f (x )=cos x ·⎝⎛⎭⎫12sin x +32cos x -3cos 2x +34 =12sin x ·cos x -32cos 2x +34=14sin 2x -34(1+cos 2x )+34=14sin 2x -34cos 2x =12sin ⎝⎛⎭⎫2x -π3. 所以f (x )的最小正周期T =2π2=π. (2)因为f (x )在区间⎣⎡⎦⎤-π4,-π12上是减函数,在区间⎣⎡⎦⎤-π12,π4上是增函数, f ⎝⎛⎭⎫-π4=-14,f ⎝⎛⎭⎫-π12=-12,f ⎝⎛⎭⎫π4=14, 所以函数f (x )在闭区间⎣⎡⎦⎤-π4,π4上的最大值为14,最小值为-12.。