圆锥体(台)展开图

圆锥的表面积公式（圆锥的面积公式）圆柱、圆锥、圆台的表面积圆柱的侧面展开图是一个矩形。

如果圆柱的底面半径为 r ，母线长为 l ，那么圆柱的底面面积为πr²，侧面面积为2πrl 。

圆柱的表面积为S = 2 π r² + 2 π r l= 2 π r ( r + l )圆柱和圆锥展开图圆锥的侧面展开图是一个扇形。

如果圆锥的底面半径为 r，母线长为 l，圆锥的表面积为S = π r ² + π r l = π r ( r + l )圆台的侧面展开图是一个扇环，它的表面积等于上、下两个底面的面积和加上侧面的面积，即S = π ( r'² + r² + r'l+ r l )圆台展开图柱体、锥体与台体的体积柱体的体积为V = S h锥体(圆锥和棱锥)的体积为同低等高的柱体(圆柱和棱柱)的三分之一，即椎体的体积公式台体的体积为球的体积和表面积设球的半径为R，它的体积是以R为自变量的函数。

球的体积球的表面积S也是以R为自变量的函数。

球的表面积证明题祖暅原理与柱体、椎体、台体及球体的体积祖暅原理: “幂势既同，则积不容异”。

“ 幂”即面积，“ 势”即高，这原理是说，夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何平面所截，如果截得的两个截面的面积总相等，那这两个几何体的体积一定相等。

祖暅原理根据祖先杵的原理，可以推导出两个等底等高椎体的体积相等。

用祖暅原理推导几何体的体积公式设有底面积都等于S，高都等于h的两个锥体(或柱体)，使它们的底面在同一平面内。

根据祖暅原理，可推导出它们的体积相等。

① ②根据图② 可得三棱锥的体积等于棱柱体积的三分之一。

应用祖暅原理研究半球(半径为R)的体积计算:设平行于大圆且与大圆的距离为ι 的平面截半球所得圆面的半径为 r，r = √( R²-ι² )，于是截面面积S1 = π r² =π (R²-ι²) = πR² - πι²S1 可以看成是在半径为 R 的圆面上挖去一个半径为 l 的同心圆，所得圆环的面积。

圆台侧面的展开的两种方法
圆台是圆锥平行地切去顶部得到的剩下的一部分，它的上底面和下底面平行，圆台的立体图见Fig 1：
Fig 1 圆台实图
如果沿着圆台的母线即剪开圆台，如图Fig 2，并展开剪下来的图形，那么会得到什么样的图形呢，下面我们从两个思路出发解答这个问题。

Fig 2 圆台立体图
第一种方法：利用圆台的定义。

圆台是圆锥平行地切去顶部得到的剩下的一部分，那么是不是可以从圆锥的展开图中得到圆台的展开图呢，而圆锥的展开图是一个扇形，这是大家都知道的，圆锥的立体图和展开图如图Fig 3(a)和Fig 3(b)。

Fig 3(a) 圆锥立体图Fig 3(b) 圆锥展开图
这样我们想象把圆锥剪开和圆台剪开的区别，就是一个大圆锥减去一个相似的小圆锥就是圆台，那么对应的展开图也是一样一个大扇形减去一个小扇形，就是圆台的展开图，如图Fig 4。

Fig 4 圆台展开图
第二种方法：想象圆锥极端的情形。

如果把圆锥的锥角看成0度，那么圆台也就变成了圆柱，而圆柱我们是知道的，它的展开图是一个矩形，这个时候母线与底面曲线展开的曲线（弧度为无穷，变成了直线）是垂直的，那么换成圆台显然就不垂直了，而是和底面曲线展开的圆弧的切线垂直，那么就得到了如图Fig 4的图形。

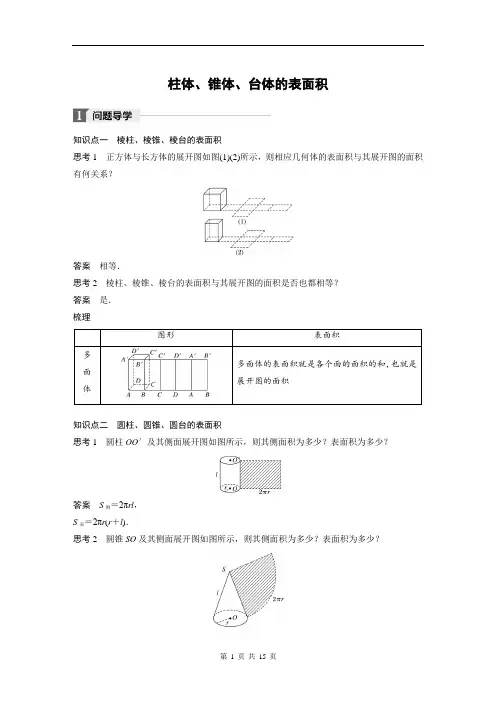
柱体、锥体、台体的表面积知识点一棱柱、棱锥、棱台的表面积思考1正方体与长方体的展开图如图(1)(2)所示，则相应几何体的表面积与其展开图的面积有何关系？答案相等．思考2棱柱、棱锥、棱台的表面积与其展开图的面积是否也都相等？答案是．梳理图形表面积多面体多面体的表面积就是各个面的面积的和，也就是展开图的面积知识点二圆柱、圆锥、圆台的表面积思考1圆柱OO′及其侧面展开图如图所示，则其侧面积为多少？表面积为多少？答案S侧＝2πrl，S表＝2πr(r＋l)．思考2圆锥SO及其侧面展开图如图所示，则其侧面积为多少？表面积为多少？答案底面周长是2πr，利用扇形面积公式得S侧＝12×2πrl＝πrl，S表＝πr2＋πrl＝πr(r＋l)．思考3圆台OO′及其侧面展开图如图所示，则其侧面积为多少？表面积为多少？答案如图，圆台的侧面展开图是扇环，内弧长等于圆台上底周长，外弧长等于圆台下底周长，如图，xx＋l＝rR，解得x＝rR－rl.S扇环＝S大扇形－S小扇形＝12(x＋l)×2πR－12x·2πr＝π[(R－r)x＋Rl]＝π(r＋R)l，所以S圆台侧＝π(r＋R)l，S圆台表＝π(r2＋rl＋Rl＋R2)．梳理图形表面积公式旋转体圆柱底面积：S底＝2πr2侧面积：S侧＝2πrl表面积：S＝2πr(r＋l)圆锥底面积：S底＝πr2侧面积：S侧＝πrl表面积：S＝πr(r＋l)圆台上底面面积：S上底＝πr′2下底面面积：S下底＝πr2侧面积：S侧＝π(r′l＋rl)表面积：S＝π(r′2＋r2＋r′l＋rl)类型一 棱柱、棱锥、棱台的侧面积与表面积例1 (1)如图所示，在斜三棱柱ABC －A 1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝a ，∠AA 1B 1＝∠AA 1C 1＝60°，∠BB 1C 1＝90°.侧棱长为b ，则其侧面积为( )A.334abB.3＋22ab C ．(3＋2)ab D.23＋22ab答案 C解析 斜棱柱的侧面积等于各个侧面面积之和，斜棱柱的每个侧面都是平行四边形．由题意知斜三棱柱的底面是等腰直角三角形．∵AB ＝AC ＝a ，∴BC ＝2a . ∵∠AA 1B 1＝∠AA 1C 1＝60°，AB ＝AC ＝a ，AA 1＝b ， ∴1111＝ACC A ABB A SS＝ab sin 60°＝32ab . 又∵∠BB 1C 1＝90°，∴侧面BB 1C 1C 为矩形， ∴11矩形BB C C S ＝2ab ，∴S 斜三棱柱侧＝32ab ＋32ab ＋2ab ＝(3＋2)ab . 故选C.(2)已知正四棱台(上、下底是正方形，上底面的中心在下底面的投影是下底面中心)上底面边长为6，高和下底面边长都是12，求它的侧面积．解 如图，E 、E 1分别是BC 、B 1C 1的中点，O 、O 1分别是下、上底面正方形的中心，则O 1O 为正四棱台的高，则O 1O ＝12.连接OE 、O 1E 1， 则OE ＝12AB ＝12×12＝6，O 1E 1＝12A 1B 1＝3.过E 1作E 1H ⊥OE ，垂足为H ， 则E 1H ＝O 1O ＝12，OH ＝O 1E 1＝3， HE ＝OE －O 1E 1＝6－3＝3.在Rt △E 1HE 中，E 1E 2＝E 1H 2＋HE 2＝122＋32＝153， 所以E 1E ＝317.所以S 侧＝4×12×(B 1C 1＋BC )×E 1E＝2×(6＋12)×317＝10817. 引申探究本例(2)中，把棱台还原成棱锥，你能利用棱锥的有关知识求出棱台的侧面积吗？ 解 如图，将正四棱台的侧棱延长交于一点P .取B 1C 1、BC 的中点E 1、E ，则EE 1的延长线必过P 点．O 1、O 分别是正方形A 1B 1C 1D 1与正方形ABCD 的中心．由正棱锥的定义，CC 1的延长线过P 点， 且有O 1E 1＝12A 1B 1＝3，OE ＝12AB ＝6，则有PO 1PO ＝O 1E 1OE ＝36，即PO 1PO 1＋O 1O ＝12，所以PO 1＝O 1O ＝12.在Rt △PO 1E 1中，PE 21＝PO 21＋O 1E 21＝122＋32＝153， 在Rt △POE 中，PE 2＝PO 2＋OE 2＝242＋62＝612， 所以E 1E ＝PE －PE 1＝617－317＝317. 所以S 侧＝4×12×(BC ＋B 1C 1)×E 1E＝2×(12＋6)×317＝10817.反思与感悟 棱锥及棱台的表面积计算常借助斜高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解．跟踪训练1 已知正三棱锥V －ABC 的正视图、俯视图如图所示，其中VA ＝4，AC ＝23，求该三棱锥的表面积．解 由正视图与俯视图可得正三棱锥的直观图，如图所示，且VA＝VB＝VC＝4，AB＝BC＝AC＝23，取BC的中点D，连接VD，则VD⊥BC，所以VD＝VB2－BD2＝42－(3)2＝13，则S△VBC＝12VD·BC＝12×13×23＝39，S△ABC＝12×(23)2×32＝33，所以三棱锥V－ABC的表面积为3S△VBC＋S△ABC＝339＋33＝3(39＋3)．类型二圆柱、圆锥、圆台的侧面积与表面积例2(1)已知圆柱与圆锥的高、底面半径分别相等．若圆柱的底面半径为r，圆柱的侧面积为S，则圆锥的侧面积为________．答案4π2r4＋S22解析设圆柱的高为h，则2πrh＝S，∴h＝S 2πr.设圆锥的母线为l，∴l＝r2＋h2＝r2＋S24π2r2.∴圆锥的侧面积为πrl＝πr r2＋S24π2r2＝4π2r4＋S22.(2)圆台的上、下底面半径分别为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°，那么圆台的表面积是________．(结果中保留π)答案 1 100π cm2解析如图所示，设圆台的上底面周长为c，因为扇环的圆心角是180°，故c＝π·SA＝2π×10，所以SA＝20，同理可得SB＝40，所以AB＝SB－SA＝20，所以S 表面积＝S 侧＋S 上＋S 下＝π(r 1＋r 2)·AB ＋πr 21＋πr 22＝π(10＋20)×20＋π×102＋π×202＝1 100π(cm 2)． 故圆台的表面积为1 100π cm 2.反思与感悟 解决台体的问题通常要还台为锥，求面积时要注意侧面展开图的应用，上、下底面圆的周长是展开图的弧长．跟踪训练2 (1)一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比是( ) A.1＋2π2πB.1＋2π4πC.1＋2ππD.1＋4π2π答案 A解析 设圆柱的母线长为l ，∴l ＝2πr ，r ＝l2π，则圆柱的表面积为2πr 2＋l 2＝2πl 24π2＋l 2＝2π＋12πl 2，侧面积为l 2， ∴圆柱的表面积与侧面积的比是2π＋12πl 2∶l 2＝2π＋12π.故选A.(2)轴截面是正三角形的圆锥称作等边圆锥，则等边圆锥的侧面积是底面积的( ) A ．4倍 B ．3倍 C.2倍 D ．2倍 答案 D解析 设圆锥底面半径为r ，由题意知母线长l ＝2r ，则S 侧＝πr ×2r ＝2πr 2，∴S 侧S 底＝2πr 2πr 2＝2. 类型三 简单组合体的表面积例3 如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A ．20πB ．24πC ．28πD ．32π 答案 C解析 由三视图可知，组合体的底面圆的面积和周长均为4π，圆锥的母线长l ＝(23)2＋22＝4，所以圆锥的侧面积为S锥侧＝12×4π×4＝8π，圆柱的侧面积S 柱侧＝4π×4＝16π，所以组合体的表面积S ＝8π＋16π＋4π＝28π，故选C.反思与感悟 求组合体的表面积，首先弄清它的组成，其表面有哪些底面和侧面，各个面应怎样求面积，然后根据公式求出各面的面积，最后再相加或相减．跟踪训练3 某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是______ cm 2.答案 7＋ 2解析 其直观图如图．由直观图可知，该几何体为一个正方体和一个三棱柱的组合体， ∴其表面积S ＝6×(1×1)＋2×12×1×1＋1×2＝7＋ 2.1．圆柱的轴截面是正方形，且轴截面面积是S ，则它的侧面积是( ) A.Sπ B ．πS C ．2πS D ．4πS 答案 B解析 ∵圆柱的轴截面是正方形，且轴截面面积是S ， ∴圆柱的母线长为S ，底面圆的直径为S ， ∴圆柱的侧面积S ＝π×S ×S ＝πS . 故选B.2．如图，已知ABCD －A 1B 1C 1D 1为正方体，则正四面体D －A 1BC 1的表面积与正方体的表面积之比是( )A.22 B.33C. 3D. 2 答案 B解析 设正方体的棱长为1，则正方体的表面积为6，正四面体D －A 1BC 1的棱长为2，表面积为4×12×2sin 60°×2＝23，∴正四面体D －A 1BC 1的表面积与正方体的表面积之比是33，故选B. 3．圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，则圆台的侧面积为( ) A ．100π B ．81π C ．169π D ．14π 答案 A解析 ∵圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，设圆台上底面的半径为r ，则下底面半径和高分别为4r 和4r ，由100＝(4r )2＋(4r －r )2，得r ＝2，故圆台的侧面积等于π(r ＋4r )×l ＝π(2＋8)×10＝100π，故选A.4．表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________． 答案 2解析 设圆锥的母线为l ，圆锥底面半径为r ，则12πl 2＋πr 2＝3π，πl ＝2πr ，∴r ＝1，即圆锥的底面直径为2.5．直角三角形的两条直角边长分别为15和20，以它的斜边为轴旋转生成的旋转体，求旋转体的表面积．解 设此直角三角形为ABC ，AC ＝20，BC ＝15，AC ⊥BC ，则AB ＝25.过C 作CO ⊥AB 于点O ，直角三角形绕AB 所在直线旋转生成的旋转体，它的上部是圆锥(1)，它的下部是圆锥(2)，两圆锥底面圆相同，其半径是OC ，且OC ＝20×1525＝12，圆锥(1)的侧面积S 1＝π×12×20＝240π，圆锥(2)的侧面积S 2＝π×12×15＝180π.旋转体的表面积应为两个圆锥侧面积之和，即S ＝S 1＋S 2＝420π.1．多面体的表面积为围成多面体的各个面的面积之和．2．有关旋转体的表面积的计算要充分利用其轴截面，就是说将已知条件尽量归结到轴截面中求解．而对于圆台有时需要将它还原成圆锥，再借助相似的相关知识求解． 3．S 圆柱表＝2πr (r ＋l )；S 圆锥表＝πr (r ＋l )；S 圆台表＝π(r 2＋rl ＋Rl ＋R 2)．课时作业一、选择题1．如图所示，圆锥的底面半径为1，高为3，则圆锥的表面积为( )A ．πB ．2πC ．3πD ．4π答案 C解析 设圆锥的母线长为l ，则l ＝3＋1＝2，∴圆锥的表面积为S ＝π×1×(1＋2)＝3π. 2．一个圆台的母线长等于上、下底面半径和的一半，且侧面积是32π，则母线长为( ) A ．2 B ．2 2 C ．4 D ．8 答案 C解析 圆台的轴截面如图所示，由题意知，l ＝12(r ＋R )，S 圆台侧＝π(r ＋R )·l ＝π·2l ·l ＝32π， ∴l ＝4.3．正四棱台的两底边长分别为1 cm,2 cm ，高是1 cm ，它的侧面积为( ) A ．6 cm 2 B.354 cm 2 C.233 cm 2 D ．3 5 cm 2答案 D解析 ∵四棱台的两底边长分别为1 cm,2 cm ，高是1 cm ，∴上底边到上底中心的距离是12 cm ，下底边到下底中心的距离是1 cm ，那么梯形的高，就是斜高为12＋(1－12)2＝52(cm)，一个梯形的面积就是12(1＋2)×52＝354(cm 2)，∴棱台的侧面积S ＝35(cm 2)． 故选D.4．某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为4的等腰三角形，侧视图是一个底边长为6、高为4的等腰三角形，则该几何体的表面积为( )A ．80B ．242＋88C ．242＋40D ．118答案 B解析 根据题意，可得该几何体是底面是边长分别为6和8的矩形且侧棱长均相等的四棱锥，高为SO ＝4，如图所示，因此，等腰三角形SAB 的高SE ＝SO 2＋OE 2＝42＋32＝5， 等腰三角形SCB 的高SF ＝SO 2＋OF 2＝42＋42＝42， ∴S △SAB ＝S △SCD ＝12×AB ×SE ＝20，S △SCB ＝S △SAD ＝12×CB ×SF ＝122，∵矩形ABCD 的面积为6×8＝48， ∴该几何体的表面积为S 表＝S △SAB ＋S △SCD ＋S △SCB ＋S △SAD ＋S ABCD ＝2×20＋2×122＋48＝242＋88. 故选B.5．一个直角三角形的直角边分别为3与4，以其直角边为旋转轴，旋转而成的圆锥的侧面积为( )A ．15πB ．20πC ．12πD ．15π或20π 答案 D解析 以直角三角形的直角边为旋转轴，旋转而成的圆锥，有以下两种情况： 根据圆锥的侧面积计算公式S 侧面积＝πr ×l 母线长．①以直角边3为旋转轴时，旋转而成的圆锥的侧面积S＝4π×5＝20π；②以直角边4为旋转轴时，旋转而成的圆锥的侧面积S＝3π×5＝15π.故选D.6．一个几何体的三视图如图所示，则该几何体的表面积为()A．372 B．360 C．292 D．280答案 B解析由三视图可知该几何体是由下面一个长方体，上面一个长方体组合而成的几何体．∵下面长方体的表面积为8×10×2＋2×8×2＋10×2×2＝232，上面长方体的表面积为8×6×2＋2×8×2＋2×6×2＝152，又∵长方体表面积重叠一部分，∴几何体的表面积为232＋152－2×6×2＝360.7．如图是一个几何体的三视图，若该几何体的表面积为9π，则该几何体的正视图中实数a 的值为()A．1 B．2 C．3 D．4答案 C解析设几何体是一个圆柱上面叠加一个圆锥，其表面积为S＝2π×1×a＋π×1×(3)2＋12＋π×12＝2πa＋3π＝9π，∴a＝3.二、填空题8．若一个圆锥的侧面展开图是半圆，则这个圆锥的底面面积与侧面积的比是________．答案1∶2解析设该圆锥体的底面半径为r，母线长为l，根据题意得2πr＝πl，所以l＝2r，所以这个圆锥的底面面积与侧面积的比是 πr 2∶12πl 2＝r 2∶12(2r )2＝1∶2.故答案为1∶2.9．一个几何体的三视图如图所示，其正视图和侧视图都是底边长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是________．答案 12π解析 由三视图知该几何体是一个圆台，其上、下底面的半径分别为2,1，母线长为4，则该几何体的侧面积S ＝π(2×4＋1×4)＝12π.10．如图所示，一个正四棱锥(底面是正方形，从顶点向底面引垂线，垂足是底面中心的四棱锥)的正方形底面的边长为4 cm ，高与斜高的夹角为30°，则正四棱锥的表面积为____ cm 2.答案 48解析 ∵该四棱锥的侧面是底边长为4 cm 的全等的等腰三角形，∴要求侧面积，只需求等腰三角形底边上的高即可，可构造直角三角形求解．如题图所示，正四棱锥的高、斜高、底面边心距组成Rt △POE . ∵OE ＝2 cm ，∠OPE ＝30°， ∴斜高PE ＝OE sin 30°＝212＝4(cm)．∴S 棱锥侧＝4·12·BC ·PE ＝4×12×4×4＝32(cm 2)，∴S 表＝S 侧＋S 底＝32＋4×4＝48(cm 2)．11．如图所示，在棱长为4的正方体上底面中心位置打一个直径为2、深为4的圆柱形孔，则打孔后的几何体的表面积为________．答案96＋6π解析由题意知，所打圆柱形孔穿透正方体，因此打孔后所得几何体的表面积等于正方体的表面积，再加上一个圆柱的侧面积，同时减去两个圆的面积，即S＝6×42＋4×2π－2π×12＝96＋6π.三、解答题12．如图所示是某几何体的三视图，它的正视图和侧视图均为矩形，俯视图为正三角形．(长度单位：cm)(1)该几何体是什么图形？(2)画出该几何体的直观图(坐标轴如图所示)，并求它的表面积.(只需作出图形，不要求写作法) 解(1)由三视图可知该几何体是三棱柱．(2)直观图如图所示．因为该几何体的底面是边长为4 cm的等边三角形，高为2 cm，所以它的表面积S三棱柱＝2S底＋S侧＝2×34×42＋3×4×2＝(24＋83)(cm2)．13．如图，已知正三棱锥S－ABC的侧面积是底面积的2倍，正三棱锥的高SO＝3，求此正三棱锥的表面积．解 如图，设正三棱锥的底面边长为a ，斜高为h ′.过点O 作OE ⊥AB ，与AB 交于点E ，连接SE ，则SE ⊥AB ，SE ＝h ′.∵S 侧＝2S 底，∴12×3a ×h ′＝34a 2×2，∴a ＝3h ′.∵SO ⊥OE ，∴SO 2＋OE 2＝SE 2， ∴32＋(36×3h ′)2＝h ′2，∴h ′＝23，∴a ＝3h ′＝6. ∴S 底＝34a 2＝34×62＝93，S 侧＝2S 底＝183， ∴S 表＝S 侧＋S 底＝183＋93＝27 3. 四、探究与拓展14．已知某圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则该圆台较小底面的半径为( ) A ．7 B ．6 C ．5 D ．3 答案 A解析 设圆台较小底面的半径为r ，则另一底面的半径为3r .由S 侧＝3π(r ＋3r )＝84π，解得r ＝7.15．如图，一个圆锥的底面半径为1，高为3，在圆锥中有一个半径为x 的内接圆柱．(1)试用x 表示圆柱的高；(2)当x 为何值时，圆柱的侧面积最大，最大侧面积是多少？ 解 (1)设所求的圆柱的底面半径为x ，它的轴截面如图，BO ＝1，PO ＝3，圆柱的高为h ，由图，得x 1＝3－h3，即h ＝3－3x .(2)∵S 圆柱侧＝2πhx ＝2π(3－3x )x ＝6π(x －x 2)， 当x ＝12时，圆柱的侧面积取得最大值为32π.∴当圆柱的底面半径为12时，它的侧面积最大为32π.。

有关圆锥展开图计算的两个重要公式⼤家在解决有关圆锥侧⾯展开图的计算问题时，通常利⽤了两个等量关系，第⼀个是=×底⾯圆周长(或侧⾯的弧长)×母线长，第⼆个就是侧⾯的弧长等于底⾯的周长，但每次都直接利⽤这两个等量关系来计算还是很⿇烦，特别是同学们往往容易忘记乘以系数，基于此我们不妨把这两个等量关系进⼀步推导，得出实质性的乘积、⽐例公式。

我相信同学们在理解并运⽤这两个公式后，解题的思路可以变得清晰，速度和准确度也可以得到很⼤的提⾼。

⼀、推导公式：1.乘积式：侧⾯积：全⾯积：2.⽐例式：弧长等于⊙O1的周长∵∴⼜∵即：这两组公式的优点是避开了求底⾯圆周长，⽽直接建⽴了S侧与R、r的乘积关系，以及圆⼼⾓n与R、r的⽐例关系，减少了许多中间过程，特别是⽐例式给我们的计算带来了极⼤的便利。

⼆、运⽤乘积式：类型⼀：顺向使⽤公式【问题】（2009济南）在综合实践活动课上，⼩明同学⽤纸板制作了⼀个圆锥形漏⽃模型．如图所⽰，它的底⾯半径⾼则这个圆锥漏⽃的侧⾯积是（）A．　B． C． D．分析：从刚才推导出的可以看出，只与圆锥的母线长度以及底⾯圆半径有关，若题⽬没有直接给出母线长度以及底⾯圆半径，往往还可以利⽤R、r和h组成的直⾓三⾓形，求出未知的R 或r来，从⽽计算出侧⾯积。

结论：要求,就求R、r。

解答：此题由底⾯半径⾼可以求出母线BC为10cm，即R=10cm，r=6cm，再由，选C。

【练习】1. （2009铁岭）⼩丽想⽤⼀张半径为5cm的扇形纸⽚围成⼀个底⾯半径为4cm的圆锥，接缝忽略不计，则扇形纸⽚的⾯积是cm2．（结果⽤表⽰）202.（2009南昌）⼀个圆锥的底⾯直径是80cm,母线长是90cm,则它的侧⾯积是____ 。

3600cm23. （2008成都）⼩红同学要⽤纸板制作⼀个⾼4cm，底⾯周长是6πcm的圆锥形漏⽃模型，若不计接缝和损耗，则她所需纸板的⾯积是（）BA．12πcm2 B．15πcm2 C．18πcm2 D．24πcm2类型⼆：逆向使⽤公式【问题】（2009义乌）如图，圆锥的侧⾯积为，底⾯半径为3，则圆锥的⾼AO为 .分析：从刚才推导出的可以看出，已知、R、r中任意两个量可以求出余下未知的量，若题⽬要求求出圆锥的⾼h，往往还可以利⽤R、r和h组成的直⾓三⾓形，从⽽求出。

圆锥的侧面展开图教学目标1、知识与技能：了解圆锥的侧面、底面、高、轴、母线、过轴的截面等概念，了解圆锥的侧面展开图是扇形：使学生会计算圆锥的侧面积或表面积.教学重点：1、圆锥的形成手段和圆锥的轴、母线、高等概念及其特征；2、用展开图的面积公式计算圆锥的侧面积和表面积。

教学难点：对侧面积的计算和理解。

1. 圆周长：r 2C π=圆面积：2r S π=2. 圆的面积C 与半径R 之间存在关系R 2C π=，即360°的圆心角所对的弧长，因此，1°的圆心角所对的弧长就是360R 2π。

n °的圆心角所对的弧长是180R n π 180R n π=∴l *这里的180、n 在弧长计算公式中表示倍分关系，没有单位。

3. 由组成圆心角的两条半径和圆心角所对的弧所围成的圆形叫做扇形。

发现：扇形面积与组成扇形的圆心角的大小有关，圆心角越大，扇形面积也就越大。

4. 在半径是R 的圆中，因为360°的圆心角所对的扇形的面积就是圆面积2R S π=，所以圆心角为n °的扇形面积是：R 21360R n S 2l =π=扇形（n 也是1°的倍数，无单位） 5. 圆锥的概念观察模型可以发现：圆锥是由一个底面和一个侧面围成的。

其中底面是一个圆，侧面是一个曲面，如果把这个侧面展开在一个平面上，展开图是一个扇形。

如图，从点S 向底面引垂线，垂足是底面的圆心O ，垂线段SO 的长叫做圆锥的高，点S叫做圆锥的顶点。

锥也可以看作是由一个直角三角形旋转得到的。

也就是说，把直角三角形SOA 绕直线SO 旋转一周得到的图形就是圆锥。

其中旋转轴SO 叫做圆锥的轴，圆锥的轴通过底面圆的圆心，并且垂直于底面。

另外，连结圆锥的顶点和底面圆上任意一点的线段SA 、SA 1、SA 2、……都叫做圆锥的母线，显然，圆锥的母线长都相等。

母线定义：连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。