24-4 相对论的动量和能量
- 格式:ppt
- 大小:1.38 MB
- 文档页数:17


相对论中能量和动量的关系式为1. 能量与动量的基础知识在聊能量和动量之前,咱们先来个小引子。
想象一下,你在公园里看到一个小孩推着滑板车,哇,那推力可是大了!这小家伙冲得飞快,简直像个小火箭!这时候,大家可能会想,为什么滑板车能跑得那么快?这就要提到能量和动量的关系了。
能量就像是小孩的“燃料”,而动量则是那种“冲劲”。
简单来说,能量和动量就像是两个好朋友,永远在一起,互相帮助。
1.1 能量的定义能量,听上去高大上,但其实就是物体所拥有的能力。
无论是动能、势能,还是其他类型的能量,都是为了让物体能动起来、能改变状态。
打个比方,就像你饿的时候需要吃饭,吃饱了才能有力气去玩耍一样,物体也需要能量才能动。
1.2 动量的定义再说说动量,动量其实就是物体运动的“重头戏”。
它的大小和物体的质量还有速度有关。
简单来说,质量大、速度快的物体,动量就大,反之亦然。
就像你一脚踩上去的泥巴,越重越难动,越快越滑!这就是真实的动量作用。
2. 相对论的魅力现在我们把视角转到相对论上。
爱因斯坦真的是个天才!他的相对论把我们对时间和空间的理解完全颠覆了。
就像是打开了一扇新世界的大门,里面满是神奇的东西。
特别是能量和动量的关系式,更是让人耳目一新。
2.1 公式背后的故事在相对论中,能量和动量的关系可以用一个公式来表达,简直像是数学界的魔法咒语!这个公式说的就是:能量等于动量乘以光速,再加上静止质量的能量。
听起来有点复杂?其实它想告诉我们,物体的能量和动量并不是孤立的,它们总是紧紧联系在一起。
2.2 生活中的例子我们来点生活中的例子,假设你在超市推购物车。
购物车越满,你推起来越费力,对吧?这就是因为动量和能量在起作用。
你推的力度(能量)和购物车的速度(动量)都在影响着你购物的体验。
想象一下,等你推到结账的地方,满载而归,心里那种成就感,简直无与伦比!3. 深入理解能量与动量的关系最后,我们来深入挖掘一下这对好朋友的关系。
能量和动量就像是一对密不可分的恋人,互相依赖,互相促进。

相对论中的能量动量关系在物理学中,相对论是一种描述物质和能量如何在空间和时间中相互作用的理论。
爱因斯坦的狭义相对论和广义相对论无疑是相对论的两大里程碑。
其中,相对论中的能量动量关系是一个非常重要的概念,它揭示了物质和能量之间关系的深度。
相对论中的能量动量关系可以从质能等价原理和质能守恒原理出发进行探讨。
质能等价原理指出,质量和能量之间存在着等价关系,即质量可以转化为能量,能量也可以转化为质量。
这一原理被广泛应用于核能的释放及利用、核反应的平衡等领域。
质能守恒原理则是指在相对论中,对于一个封闭系统来说,其质量和能量之和保持不变。
根据狭义相对论的基本原则,物质的能量与其质量的关系可以表示为 E = mc²,其中E表示物体的能量,m表示物体的质量,c表示光速。
爱因斯坦引入了能动量四矢量的概念,它包括了能量和动量在空间和时间上的分量。
能动量四矢量表示为P = (E/c, p),其中E/c为能量分量,p为动量分量。
这样,相对论中的能量动量关系可以表示为P² = (E/c)² - (pc)² = m²c²,其中m是物体的静止质量。
从这个公式中可以看出,当物体的速度接近光速时,其动量分量也会接近无穷大。
这意味着质量越大的物体,其速度接近光速时所具有的动量也趋于无穷大。
相对论中的能量动量关系对于解释一些奇特现象非常重要,比如质子在加速器中达到光速时所具有的动量非常大,而且可以与高能粒子作用产生新的粒子。
此外,能量动量关系还揭示了光子的存在,光子是相对论中能量为零质量为常数的粒子。
相对论中的能量动量关系也可以解释物体的质量增加原理。
当物体的速度接近光速时,其动能增加,相应地,它的质量也会相对增加。
这一现象在实验中被证实过,例如,加速器中的粒子被加速到非常高的速度后其质量会增加,这也是质子在加速器中需要不断增大加速器能量的原因。
总而言之,相对论中的能量动量关系是揭示物质和能量之间相互转化关系的重要观念。


相对论能量动量关系相对论能量动量关系是狭义相对论中的一个重要概念,它描述了物体的能量和动量之间的相互关系。
根据相对论的观点,能量和动量不再是独立的物理量,而是相互联系的。
在经典力学中,能量和动量分别被定义为物体的质量和速度的函数。
然而,在相对论中,质量不再是一个固定的值,而是与速度相关的量。
根据相对论的质能关系,物体的能量与其质量之间存在着等价关系,即E=mc²,其中E代表能量,m代表物体的质量,c代表光速。
根据质能关系,我们可以推导出相对论能量动量关系的公式。
根据狭义相对论的基本原理,物体的能量和动量应该满足以下关系:E² = (pc)² + (mc²)²,其中p代表物体的动量。
通过推导和计算,我们可以得到相对论能量动量关系的具体表达式:E² = (mc²)² + (pc)²,其中E代表物体的能量,m代表物体的质量,p代表物体的动量,c代表光速。
相对论能量动量关系的一个重要结论是,物体的能量和动量不再是线性关系,而是非线性的。
当物体的速度接近光速时,能量和动量的增长速度也会趋于无穷大。
这意味着,相对论效应在高速运动物体的能量和动量中发挥了重要作用。
相对论能量动量关系不仅对粒子物理学和高能物理学有着重要的实际应用,也对我们理解宇宙的起源和演化提供了深刻的见解。
通过研究物体的能量和动量之间的关系,我们可以更好地理解宇宙中各种粒子的运动和相互作用,从而揭示宇宙的奥秘。
在实际应用中,相对论能量动量关系被广泛应用于核能源、粒子加速器和粒子物理实验等领域。
通过测量物体的能量和动量,科学家们可以推断物体的质量和速度,进而研究物体的性质和相互作用规律。
相对论能量动量关系是狭义相对论中的一个重要概念,描述了物体的能量和动量之间的相互关系。
相对论能量动量关系的推导和应用使我们对物质世界有了更深入的理解,为我们解开宇宙奥秘和推动科学技术的发展提供了重要的理论基础。

相对论中能量动量关系怎么推能量-动量关系是相对论中最为重要的公式之一,它描述了物体的质量和速度之间的关系。
推导能量-动量关系需要使用狭义相对论的基本假设,即所有惯性参考系之间的物理规律都是相同的。
首先,我们定义一个质量为m的物体的动能:E_k = \frac{1}{2}mv^2其中,v是物体的速度。
接下来,根据相对论的基本假设,我们考虑两个不同的惯性参考系,分别为S和S'。
这两个参考系之间存在相对运动,其速度为v。
在S参考系中,物体的动量为:p = mv同时,在S'参考系中,物体的动量为:p' = \frac{mv}{\sqrt{1 - \frac{v^2}{c^2}}}其中,c是光速。
接下来,我们考虑在S'参考系中,物体的动能:E_k' = \frac{1}{2}m\frac{v^2}{1 - \frac{v^2}{c^2}}现在我们可以使用相对论能量-动量守恒定律来推导能量动量关系:E_k + E = E_k' + E' + K其中,E是物体的静能量,K是相对于S参考系的总动量,E'是相对于S'参考系的总能量。
根据相对论的动量-能量关系,我们可以将K和E'表示为:K = \frac{p^2}{2m}E' = \frac{mc^2}{\sqrt{1 - \frac{v^2}{c^2}}}这样,我们就可以将相对论能量动量守恒定律写成:E_k + E = \frac{m c^2}{\sqrt{1-\frac{v^2}{c^2}}} + \frac{p^2}{2m}这就是著名的能量动量关系,其中E_k是物体的动能,E是静能,p是物体的动量,m是物体的质量,c是光速。



相对论能量动量关系的推导相对论是指爱因斯坦在1905年提出的一种物理学理论,它描述了运动物体的性质和行为,尤其是在高速运动和强引力下的物理现象。
其中,相对论能量动量关系是相对论的重要基础之一,也是研究物体在高速运动中的能量和动量变化的关键。
相对论能量动量关系的推导可以通过以下步骤来完成:1. 引言相对论是爱因斯坦提出的一种描述高速运动物体的理论,相对论中的能量和动量概念与经典物理有所不同。
本文将从相对论的角度推导能量动量关系。
2. 相对论基本假设相对论基于两个基本假设:光速恒定和时空的相对性。
基于这两个假设,相对论建立了一套完整的数学框架来描述物体在不同参考系中的性质和行为。
3. 能量和动量定义在相对论中,能量和动量不再是简单的物体的物理量,而是与其运动速度有关的变量。
相对论能量定义为E = γmc²,其中γ是洛伦兹因子,m是物体的静止质量,c是光速。
动量定义为p = γmv,其中v是物体的运动速度。
4. 相对论能量动量关系的推导a. 考虑一个静止质量为m的物体,其静止能量为E₀ = mc²,动量为p₀ = 0。
b. 若物体以速度v运动,则根据动量定义,其动量为p = γmv。
c. 将动量代入能量定义中,可以得到物体在运动状态下的能量表达式为E = γmc² = E₀ + T,T表示动能的增量。
d. 对能量表达式进行化简和变换,可以得到E² = p²c² + m²c⁴,这就是相对论中的能量动量关系。
5. 能量动量关系的性质a. 能量动量关系表明,物体的能量和动量不仅与静止质量有关,还与运动速度相关。
b. 当物体静止时(v = 0),能量动量关系退化为经典物理学中的表达式:E = mc²,p = 0。
c. 当物体以光速运动时(v = c),能量动量关系变为E = pc,即E与p成正比。
6. 实例分析:粒子加速器a. 相对论能量动量关系的推导对于粒子加速器中的粒子运动研究具有重要意义。

相对论能量动量关系的推导相对论是现代物理学的重要分支之一,它在解释自然界中的运动和相互作用方面起着至关重要的作用。
在相对论中,能量和动量的关系是一个基本且核心的概念。
本文将从相对论的基本原理入手,推导出能量和动量之间的关系。
相对论的基本原理之一是光速不变原理,即无论观察者的运动状态如何,光在真空中的速度始终保持不变。
为了推导出能量和动量之间的关系,我们需要先介绍一下相对论中的四维动量。
在相对论中,物体的四维动量由一个四分量矢量来描述,记作P=(E, p),其中E表示能量,p表示动量。
根据相对论的光速不变原理,四维动量的模是一个常数,即:P^2 = E^2 - p^2c^2 = m^2c^2其中,c代表真空中的光速,m为物体的静止质量。
上述式子称为四维动量的光锥条件,它描述了物体的能量和动量之间的关系。
接下来,我们来推导出相对论能量动量关系的具体形式。
首先,考虑一个静止粒子,其动量为零,即p = 0。
此时,光锥条件可以简化为:P^2 = E^2 - m^2c^2 = 0解得:E = mc^2这是著名的爱因斯坦质能关系式,它表明了物质与能量之间的等价性,也是相对论的重要成果之一。
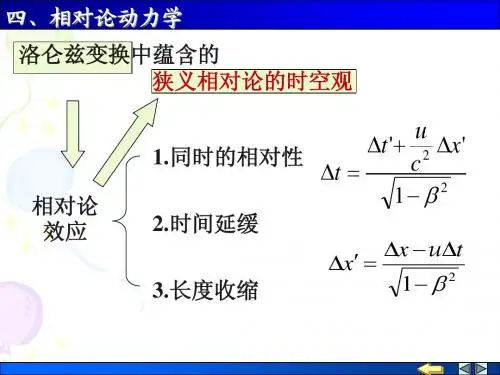
当物体以速度v运动时,它的动量不再为零,我们可以通过洛伦兹变换来推导出相对论下的能量动量关系。
根据洛伦兹变换,我们可以将物体在其静止参考系中的四维动量转换到其他任意参考系中。
假设一个物体以速度v相对于参考系S'运动,该参考系相对于静止参考系S以速度u运动。
我们用(E', p')来表示物体在S'系中的能量动量,用(E, p)来表示物体在S系中的能量动量。
根据洛伦兹变换的表达式,我们可以得到:E = γ(E' + up')p = γ(p' + uE'/c^2)其中,γ是洛伦兹因子,定义为:γ = 1/√(1 - (v/c)^2)通过代入洛伦兹变换的表达式,我们可以将上述式子化简为:E^2 = p^2c^2 + m^2c^4这就是相对论下的能量动量关系,也被称为相对论能量动量关系。
相对论动量和能量的关系式相对论动量和能量之间的关系式是相对论能量-动量关系,也称作欧拉恩关系式。
该关系式在相对论力学中起着重要作用,它揭示了质点的能量和动量如何相互转换。
相对论力学中,质点的动量p和能量E不再遵循经典物理学中的简单累加关系,而是由质点的速度v和质量m来决定。
Einsteins麦克斯韦关系给出了相对论质点的能量表达式:E² = (pc)² + (m₀c²)²其中p是相对论动量,m₀是质量,c是光速。
从这个表达式中,我们可以看到相对论能量-动量关系的一些重要特征。
首先,相对论能量和动量之间的关系不再是简单的1:1关系。
这是相对论力学的一大突破,相对于经典物理学的牛顿动力学而言,经典物理学中质点的动能与动量的关系是线性的。
在相对论力学中,能量与动量之间的关系是非线性的,即存在着一种对称变换关系。
其次,当质点的速度趋近于零时,相对论能量-动量关系退化为经典物理学中的结果。
当速度v远小于光速c时,我们可以将相对论能量-动量关系进行展开,并将高次项忽略,得到以下近似关系式:E = mc²这就是著名的相对论质能等效原理,即质量和能量之间存在一种等效关系。
第三,当质点的速度趋近于光速c时,相对论能量-动量关系的第一项(pc)²占据主导地位。
这意味着质点的能量变得相对较大,并且远远超过了质量能的贡献。
这个结果是相对论性的,与经典物理学不同。
这也解释了为什么质子,尽管质量很小,但在粒子加速器中可以获得极高的能量。
最后,相对论能量-动量关系中的平方项可解释为质点的静质能。
当质点的速度趋近于零时,平方项成为关系式的主导项,表明质量能占据主导地位。
相对论力学揭示了质点的能量来源包括动能和质量能的贡献。
综上所述,相对论动量和能量之间的关系式是E² = (pc)² +(m₀c²)²。
这个关系式包含了质点的质量、速度和能量之间的关系,揭示了质点的能量如何随着速度变化而变化,以及质点的能量如何分别由动能和质量能贡献。
相对论动能动量关系相对论动能动量关系是狭义相对论中最为经典的公式之一。
它关系到物理学中动量的概念以及质量与能量之间的转换,是研究高速运动物体行为的基础。
下面,我们将会分步骤地解释相对论动能动量关系。
1. 动量的定义动量是描述物体运动状态的一个物理量,它是物体质量乘以速度,即p=mv。
动量是一个矢量量,它有大小和方向之分。
2. 质量与能量狭义相对论中,质量不再是一个不变的物理量。
相反,它是能量和光速之间的关系所导致的,即E=mc²,其中E代表能量,m代表质量,c代表光速。
这个公式表明,在相对论中,质量和能量是互相转换的。
3. 动能公式的推导相对论动能公式如下:K = (γ-1)mc²其中K代表动能,m代表物体的质量,c代表光速,γ是洛伦兹因子,其公式为:γ = 1/√(1-v²/c²)其中v代表物体的速度。
为了推导相对论动能公式,我们先按照牛顿第二定律的公式F=ma,对物体进行受力分析。
由于物体的质量在相对论中是不是一个不变的量,因此,在进行受力分析得到加速度a后,我们便无法得到物体的速度。
于是,我们采用经典动能公式K = 1/2mv²以及光速不变的前提,通过代数的方式将能量E和动量p与速度v联系起来,并将E和p的表达式进行化简,最终得到了相对论动能公式。
4. 动量的变化和相对论动能动量关系在相对论中,一个物体的质量和速度之间存在着一种有趣的关系。
当一个物体的速度接近光速时,物体的质量会变得越来越大,动量也会变得越来越大。
与之相对应的,则是动能随着速度的变化而变化。
当物体的速度接近光速时,动能的增长速度会越来越慢。
这正是相对论中所描述的能量不断增加,动量却趋于饱和的趋势。
综上所述,相对论动能动量关系是物理学中一个十分重要的理论体系。
它连接了质量、能量、动量和速度等相互关系,为我们解释高速运动物体的运动行为提供了基础的支撑。
了解相对论中的能量和动量相对论中的能量和动量相对论是现代物理学的基础之一,是我们对世界的认知方式发生巨大变革的标志性事件。
其中,最为重要的概念便是能量和动量。
相对论颠覆了传统物理学对于物体运动的经典观念,开启了一种全新的物理学理论框架。
这个理论框架给我们说明了物体的能量和动量是如何产生,如何变化的,以及在光速下不同物体之间的相对关系。
在本文中,我们将深度探讨相对论中能量和动量的相关问题。
一、什么是相对论?相对论是一个科学的颠覆性理论,由爱因斯坦于1905年提出。
这个理论的核心观点是相对性原理:物理定律在所有惯性参照系中都相同。
这意味着,无论我们处于什么地方,我们对物理定律的观察结果都应该相同。
相对论的一个重要推论就是行进速度的相对性:我们看到别人以及物体运动的速度是相对于我们自己的速度来计算的。
随后,爱因斯坦提出了另一项原则——光速不变原理,即无论在哪里以何种速度,光速都是恒定不变的。
这一原则可以被看作是相对论的基础,因为只有在这一基础上,才能得到相对性原理的最终形式。
二、相对论中的能量在相对论中,能量和质量是等价的,这一想法可以为能量和质量间的转化提供物理基础。
其中,著名的爱因斯坦公式E=mc²便体现了质量和能量的等价性。
这个公式表明,质量可以看作一种能量形式,同时也意味着,任何物体都储存了一定数量的能量。
同时,在相对论中,我们还谈及了相对论质能和动能两个概念。
相对论质能是指一个物体由于自身的质量而拥有的能量,这个概念源于爱因斯坦的相对性原则。
相对论动能则是指物体的运动速度以及质量所共享的能量。
因为任何物体都在不断地运动,因此它都有动能,而动能又可以表现为其质能和速度的总和。
相对论动能与经典动能的表述有所不同,因为相对论动能还涉及到物体的质量。
三、相对论中的动量在经典物理学中,动量被定义为物体质量与速度的乘积。
但是,相对论告诉我们,这种定义并不够准确。
在相对论中,动量是质量乘以速度的总和,这意味着质量的变化会影响到动量的大小。
相对论的能量守恒与动量守恒相对论是爱因斯坦的伟大理论之一,它改变了人们对于时间、空间和物质的认识。
其中,相对论中的能量守恒和动量守恒是非常重要的概念。
在古典物理学中,能量守恒和动量守恒是基本定律,但当我们进入相对论领域时,这些定律会发生一些微妙的变化。
首先,让我们来探讨相对论中的能量守恒。
在相对论中,能量并不是一个独立的量,而是与物体运动的速度和质量相关的。
根据质能方程E=mc²,质量m与能量E之间存在着一种等价关系。
当物体的速度接近光速时,质量会变得越来越大,也就意味着能量也越来越高。
这就是著名的质能方程所揭示的。
相对论中的能量守恒是指在相对论速度下,系统的总能量保持不变。
这意味着能量在不同形式之间的转换是可能的,但能量的总量仍然是守恒的。
比如,当一个物体以接近光速的速度运动时,它的动能会增加,而其它形式的能量(如静能量)则会相应减少,但总能量保持恒定。
接下来,我们来探讨相对论中的动量守恒。
在相对论中,动量也不再是简单地质量乘以速度,而是一个更复杂的概念。
根据相对论动力学,动量p等于质量m乘以速度v除以根号下(1-v²/c²),其中c代表光速。
当物体的速度接近光速时,与经典力学中相比,动量会迅速增加,这是相对论效应之一。
相对论中的动量守恒是指在相对论速度下,系统的总动量保持不变。
这意味着在相对论情况下,撞击和反冲等过程中的动量转移将产生一系列非直观的效果。
例如,当一个高速运动的物体撞击另一个静止物体时,它们之间的动量将在碰撞过程中重新分配,导致两个物体的速度都会发生变化。
除了能量守恒和动量守恒,相对论还引入了质能动量守恒定律,将能量和动量统一起来。
根据这个定律,能量和动量可以相互转化,但总量保持守恒。
相对论下的质能动量守恒定律是相对论力学中的基本定律之一,它在研究微观粒子的运动和相互作用时具有重要的作用。
简而言之,相对论中的能量守恒和动量守恒代表着物理定律对于高速物体和光速接近的情况下的演化。