工程力学静力学和材料力学严圣平 课后答案

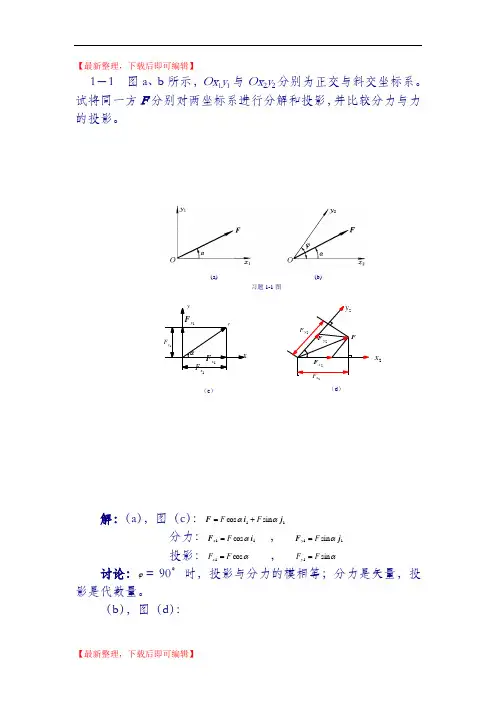
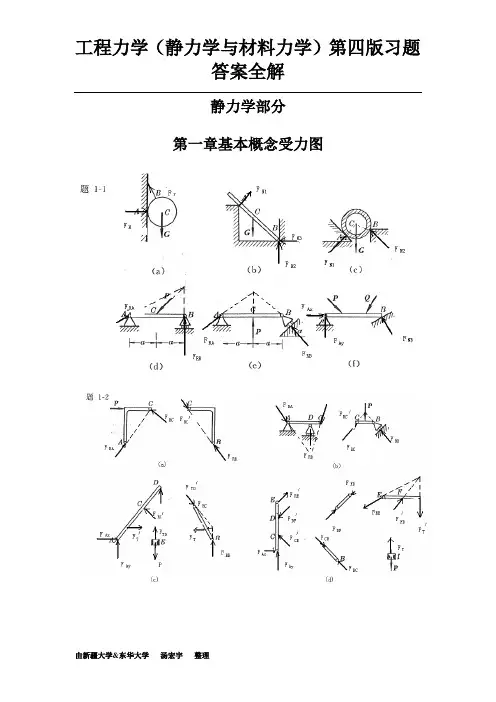
(a) (b)习题1-1图 【最新整理，下载后即可编辑】1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ），图（d ）：1y F x xF 1y Fα1xF y F（c ）2F2y F2y2x 2x F2y FF（d ）(a) (b)习题1－2图F DR AC BD AxF AyF(a-1)Ay F FB C A AxF 'F C(a-2) C DF DR(a-3)AxFF A C BD AyF (b-1) 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j FϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。

1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。

比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。

1－3 试画出图示各物体的受力图。

习题1－3图F AxFAyF D C BABF或(a-2)FB AF DCA(a-1)BF AxF AAyF C(b-1)WF BD CF FCBBF AACBF(f-1)(e-3)'A(f-2)1O(f-3)c FF AF DF BF AF A习题1－4图1－4 图a所示为三角架结构。

力F1作用在B铰上。

杆AB 不计自重，杆BD杆自重为W。

试画出图b、c、d所示的隔离体的受力图，并加以讨论。

工程力学静力学课后习题答案工程力学静力学课后习题答案引言：工程力学是一门研究物体受力和运动的学科，静力学是其中的一个重要分支。

通过学习静力学，我们可以了解物体在静止状态下受力的规律，掌握解决工程实际问题的方法和技巧。

本文将针对工程力学静力学课后习题进行解答，帮助读者更好地掌握相关知识。

一、力的平衡1. 一个物体受到两个力的作用，一个力为30N，方向为东，另一个力为40N，方向为南。

求合力的大小和方向。

解答：根据力的平衡条件，合力为0。

设合力的大小为F，方向为θ。

根据三角函数的定义，可以得到以下方程：30cosθ = 40sinθ解方程可得，θ ≈ 53.13°，F ≈ 50N。

因此，合力的大小为50N，方向为东南。

2. 一个物体质量为20kg，受到一个斜向上的力F，使其保持静止。

已知斜向上的力与水平方向的夹角为30°，求F的大小。

解答：根据力的平衡条件，物体受到的合力为0。

设F的大小为F，根据三角函数的定义，可以得到以下方程：Fsin30° = 20 * 9.8解方程可得，F ≈ 196N。

因此，F的大小为196N。

二、支持反力1. 一个物体质量为50kg，放在一个水平面上，受到一个向上的力F，使其保持静止。

已知F与水平面的夹角为60°，求支持反力的大小。

解答：根据力的平衡条件，物体受到的合力为0。

设支持反力的大小为N，根据三角函数的定义，可以得到以下方程：Nsin60° = 50 * 9.8解方程可得，N ≈ 490N。

因此，支持反力的大小为490N。

2. 一个物体质量为30kg，放在一个斜面上，斜面与水平面的夹角为30°。

已知物体沿斜面下滑的加速度为2m/s²，求斜面对物体的支持反力的大小。

解答：根据牛顿第二定律，物体所受合力等于质量乘以加速度。

设斜面对物体的支持反力的大小为N，根据三角函数的定义，可以得到以下方程：Nsin30° - 30 * 9.8 * cos30° = 30 * 2解方程可得，N ≈ 147.1N。

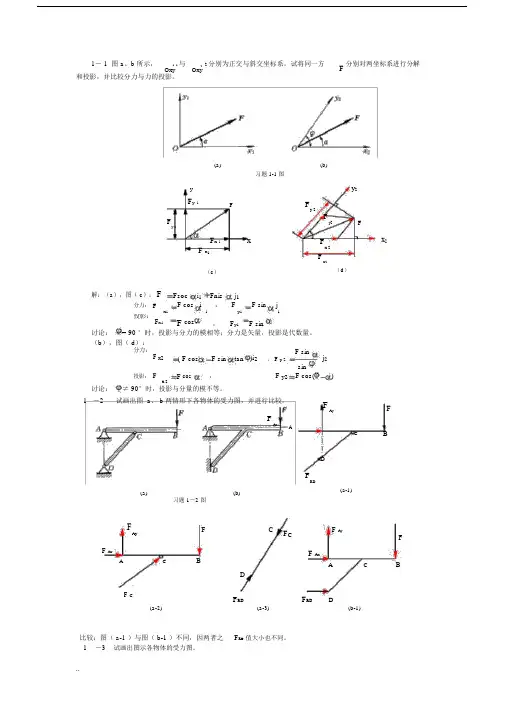
1－ 1 图 a 、b 所示，1 1与22分别为正交与斜交坐标系。

试将同一方F 分别对两坐标系进行分解OxyOxy和投影，并比较分力与力的投影。

(a) (b)习题 1-1 图yy 2F y 1FFy 2FFy 1Fy 2F x 1xFx 2x 2F x 1Fx 2（c ）（d ）解：（a ），图（ c ）： FFsoc i 1 Fnis j 1分力： Fx1 F cos i 1 ， F y1 F sinj1投影：F x1F cos， F y1 F sin讨论：= 90 °时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ），图（ d ）：分力： F x2 ( F cosF sin tan )i 2 F sinj 2， F y 2sin投影： FF cos ，F y2 F cos()x 2讨论： ≠ 90°时，投影与分量的模不等。

1 －2试画出图 a 、 b 两情形下各物体的受力图，并进行比较。

FAyFAxACDFRDFB(a)(b)(a-1)习题 1－2 图FAyFCF CF AyFF AxF AxACBA CBD'F CF RDF RDD(a-2)(a-3)(b-1)比较：图（ a-1 ）与图（ b-1 ）不同，因两者之 F R D 值大小也不同。

1 －3 试画出图示各物体的受力图。

..习题 1－3 图FDCFDC CBFF BAFAxABFAxBAF AF BFAyF BFAy(a-1)或(a-2)(b-1)CB FBDF DCF BF BABWFAxCAF AF AFAyD或(b-2) (c-1)(d-1)F CDFFCCFAxABCF cAFAyDF ABF AF D(e-1)F B或(d-2) F D(e-2)D FF O 1'CF AF O 1AF OxAFOxOOO 1FOyFOyABF AF AA ..WF B W(f-2)(e-3)(f-1)(f-3)F AF AF B1 －4 图 a 所示为三角架结构。

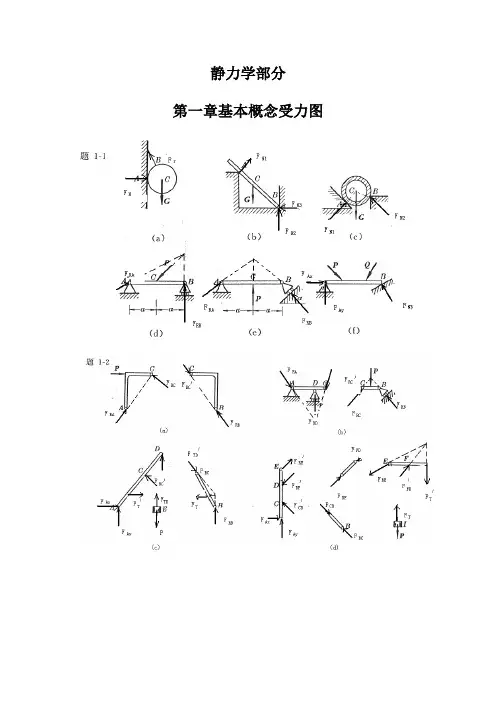
静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==o v v2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故：223R RX RY F F F KN=+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=o0Y =∑cos300AC F W -=o0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑cos 700AC AB F F -=o0Y =∑sin 700AB F W -=o1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=o o0Y =∑sin 30sin 600AB AC F F W +-=o o0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=o o0Y =∑cos30cos300AB AC F F W +-=o o0.577AB F W= (拉力)0.577AC F W= (拉力)由x =∑ 22cos 45042RA F P -=+o15.8RA F KN∴=由0Y =∑22sin 45042RA RB F F P +-=+o7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑cos 45cos 45010RA RB F F P --=o o0Y =∑sin 45sin 45010RA RB F F P -=o o联立上二式，得：22.410RA RB F KN F KN==三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=-2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CBRA F F '-=o o联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象：由0Y =∑cos 0NH CEF F α'-=CECE F F '=Q 故有：22cos 1cos 2sin cos 2sin NH P P F ααααα⎛⎫=+=⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联立后可得： 2cos 75AD AB PF F ==o取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=⋅oo由对称性及 ADAD F F '=cos5cos5222166.2cos80cos802cos 75N NDADPF F F KN '∴===⋅=o o o o o2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '-= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

工程力学——静力学与材料力学_北京工业大学中国大学mooc课后章节答案期末考试题库2023年1.关于组合变形的求解的说法错误的是（）。

参考答案:外力分析的目的是是将外载荷简化为最简形式。

2.计算挤压应力的挤压面积是指挤压接触面在垂直于挤压方向的投影面积。

参考答案:正确3.力学的研究内容（）。

参考答案:B.力学是研究物体相互作用和运动规律的科学。

4.工程力学研究的内容包括（）。

参考答案:动力学_运动学_静力学_材料力学5.静力学研究受力物体的平衡问题，不考虑物体的变形，所以把物体抽象为不变形的刚体。

参考答案:正确6.静力学部分研究对象是刚体，（）部分的研究对象是变形体。

参考答案:材料力学7.组合变形求解的基本步骤包括（）。

参考答案:外力分析。

_应力分析。

_强度分析。

_内力分析。

8.静力学研究的对象是______。

提示：刚体或变形体参考答案:刚体9.关于扭转强度和刚度，表述正确的是（）。

参考答案:扭转切应力越小，强度越大；单位长度的转角越小，扭转刚度越大。

10.偏心拉压本质上是轴向拉压与（）的组合变形。

参考答案:弯曲11.力偶对物体（）的转动时取正。

参考答案:逆时针12.一个空间任意力系，往一点平移后得到一个空间汇交力系和一个空间力偶系，空间汇交力系的合力称为该力系的________。

参考答案:主矢13.为了研究方便，一般将应力分解为与截面垂直和与截面相切两个方向的分量，与截面垂直的分量称为______参考答案:正应力14.力的三要素是（）。

参考答案:方向_大小_作用点15.在一个平面内，力偶是（）。

提示：填矢量或代数量。

参考答案:代数量16.屈服极限和强度极限是强度指标，延伸率和断面收缩率是塑性指标。

参考答案:正确17.屈服强度是屈服阶段的最______应力。

提示：填大或小参考答案:小18.屈服强度是屈服阶段的最（）应力。

提示：填大或小参考答案:小19.材料相同的圆轴，横截面面积相同的空心圆轴和实心圆轴相比，空心圆轴的强度________实心圆周的强度。

静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故： 22161.2R RX RY F F F N =+=1(,)arccos 2944RY R R F F P F '∠==o v v2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN ==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故： 223R RX RY F F F KN =+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑ sin 300AC AB F F -=o0Y =∑ cos300AC F W -=o0.577AB F W =（拉力） 1.155AC F W =（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=o0Y =∑ sin 700AB F W -=o1.064AB F W =（拉力）0.364AC F W =（压力）（c ） 由平衡方程有：0X =∑ cos 60cos300AC AB F F -=o o0Y =∑ sin 30sin 600AB AC F F W +-=o o0.5AB F W = (拉力)0.866AC F W =（压力）（d ） 由平衡方程有：0X =∑ sin 30sin 300AB AC F F -=o o0Y =∑ cos30cos300AB AC F F W +-=o o0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由0x =∑ 22cos 45042RA F P -=+o15.8RA F KN ∴= 由0Y =∑ 22sin 45042RA RB F F P +-=+o7.1RB F KN ∴=(b)解：受力分析如图所示：由 0x =∑ cos 45cos 45010RA RB F F P --=o o0Y =∑sin 45sin 45010RA RB F F P -=o o联立上二式，得： 22.410RA RB F KNF KN ==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CB RA F F '-=o o 联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联立后可得： 2cos 75AD AB PF F ==o取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=⋅oo由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N NDADP F F F KN '∴===⋅=o o o o o2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=Y=∑305BC ACF F+⋅=联立上二式得： 1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH部分，对H点列平衡x=∑05RD REF F'=Y=∑05RDF Q-=联立方程后解得：5RDF Q=2REF Q'=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

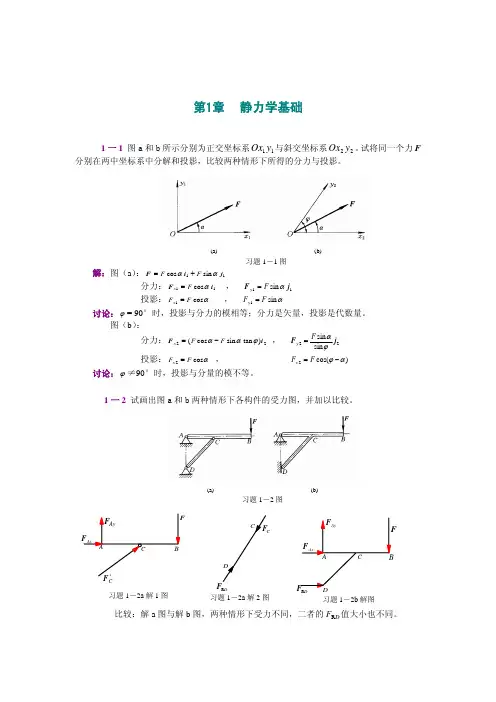
工程力学（静力学与材料力学）习题详细解答(第1章)(a) (b) 习题1－1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。

试将同一个力F 分别在两中坐标系中分解和投影，比较两种情形下所得的分力与投影。

解：图（a ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

图（b ）： 分力：22)tan sin cos (i F ϕααF F x −= ， 22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ−=F F y讨论：ϕ≠90°时，投影与分量的模不等。

1一2 试画出图a 和b 两种情形下各构件的受力图，并加以比较。

比较：解a 图与解b 图，两种情形下受力不同，二者的F R D 值大小也不同。

DR习题1－2b 解图DR习题1－2a 解2图C习题1－2a 解1图(a) (b)习题1－2图1一3 试画出图示各构件的受力图。

习题1－3图B F 习题1－3a 解2图 B习题1－3a 解1图习题1－3b 解1图F Ay Ax 习题1－3c 解图 A习题1－3b 解2图习题1－3d 解1图习题1－3e 解1图习题1－3e 解2图1－4 图a 所示为三角架结构。

荷载F 1作用在B 铰上。

AB 杆不计自重，BD 杆自重为W ，作用在杆的中点。

试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。

习题1－4图1习题1－3f 解1图F习题1－3e 解3图'A习题1－3f 解2图1O 习题1－3f 解3图F F'F 1习题1－4d 解2图F y B 21习题1－4c 解1图 AA B 1B FDx y2B 习题1－4b 解2图 1习题1－4b 解3图 F y B 2习题1－4c 解2图 F A B1B FAxF'习题1－5b 解3图E D(a-3)E B F习题1－5b 解2图习题1－5b 解1图'AxFF B习题1－5c 解图1一5 试画出图示结构中各杆的受力图。

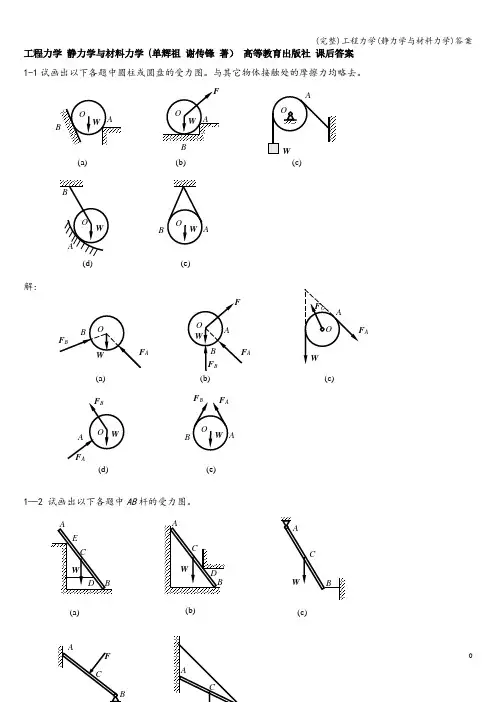
工程力学 静力学与材料力学 (单辉祖 谢传锋 著） 高等教育出版社 课后答案1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解:1—2 试画出以下各题中AB 杆的受力图。

(a)(b)(c)(d)(e)A(a)(b) A(c)A(d)(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

解：(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)(a)F(b)WA(c)（a ） 拱ABCD ；(b) 半拱AB AB ；(e) 方板ABCD ；（f ） 节点B.解:1—5 试画出以下各题中指定物体的受力图。

(a ） 结点A ,结点B ；(b ） 圆柱A 和B 及整体；（c ） 半拱AB ，半拱BC 及整体;(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

(d)D(e)F Bx(a)(b)(c)(d)(e)W(f)(a)D(b) CB(c)BF D (d) F C(e)B (f)F F BC解：(a ）(b)(c ）(d)(c)(d)ATFBAFCAACD(e)(e ）2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示,F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重,试求两杆所受的力。

解：（1） 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-6 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

BF 1F解：（1) 取DE 为研究对象,DE 为二力杆；F D = F E(2) 取ABC 为研究对象，受力分析并画受力图；画封闭的力三角形:'15166.7 23A D E F F F F N ===⨯= 3—1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。

工程力学严圣平第三版答案1．过受力构件内任一点，取截面的不同方位，各个面上的（）。

[单选题] *A. 正应力相同，切应力不同B. 正应力不同，切应力相同C. 正应力相同，切应力相同D．正应力不同，切应力不同(正确答案)2．滚动支座约束的约束反力大小未知、作用线过铰链中心、方向（）。

[单选题] *A. 与活动方向垂直(正确答案)B. 与活动方向平行C. 为铅锤方向D. 为水平方向3．对称循环时，交变应力的循环特征r =（）。

[单选题] *A．－1；(正确答案)B．0；C．0.5；D．1。

4.二力杆约束的约束反力大小未知、作用点铰链中心、方向（）。

[单选题] *A. 未知B. 平行于两个铰链的中心连线(正确答案)C. 垂直于两个铰链的中心连线D. 为水平方向5.下列说法中不正确的是：( ) [单选题] *A力使物体绕矩心逆时针旋转为负B平面汇交力系的合力对平面内任一点的力矩等于力系中各力对同一点的力矩的代数和(正确答案)C力偶不能与一个力等效也不能与一个力平衡D力偶对其作用平面内任一点的矩恒等于力偶矩，而与矩心无关6.圆轴扭转时，表面上任一点处于（）应力状态。

[单选题] *A.单向(正确答案)B.二向C.三向D.零7.梁的截面为T字型，Z轴通过横截面的形心，弯矩图如图所示，则有( )。

[单选题] *A.最大拉应力和最大压应力位于同一截面CB.最大拉应力位于截面C，最大压应力位于截面D(正确答案)C.最大拉应力位于截面D，最大压应力位于截面CD.最大拉应力和最大压应力位于同一截面D8.下列说法中不正确的是：（）。

[单选题] *A力使物体绕矩心逆时针旋转为负(正确答案)B平面汇交力系的合力对平面内任一点的力矩等于力系中各力对同一点的力矩的代数和C力偶不能与一个力等效也不能与一个力平衡D力偶对其作用平面内任一点的矩恒等于力偶矩，而与矩心无关9.低碳钢材料由于冷作硬化，会使（）提高： [单选题] *A比例极限、屈服极限(正确答案)B塑性C强度极限D脆性10.下列表述中正确的是（）。

1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB杆的受力图。

(a)B(b) (c)(d)A(e)A(a)(b)A(c)A(d)A(e)(c)(a)《工程力学》习题选解解：1-3 试画出以下各题中AB 梁的受力图。

解：(e)B B(a) B(b)(c)F B(a)(c)F (b)(d)(e)F1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD；(b) 半拱AB部分；(c) 踏板AB；(d) 杠杆AB；(e) 方板ABCD；(f) 节点B。

解：(d)D(e)F Bx(a) (b) (c)(d)D(e)W(f)(a)D(b) CB(c)BF DF《工程力学》习题选解1-5 试画出以下各题中指定物体的受力图。

(a) 结点A，结点B；(b) 圆柱A和B及整体；(c) 半拱AB，半拱BC及整体；(d) 杠杆AB，切刀CEF及整体；(e) 秤杆AB，秤盘架BCD及整体。

解：(a)(b)(c)(d)ATF BAF(b)(e)(c)(d)(e)C AA C’CDDB《工程力学》习题选解2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。