一元非线性回归

实验4.2 一元非线性回归模型实验目的熟练掌握参数初始值的数值计算以及非线性拟合的Matlab 命令，并能根据输出结果计算均方误差及可决系数，并能据此进行拟合效果分析。

实验内容解决一元非线性回归模型有以下几个步骤： （1）首先作出散点图，确定函数)(x f 的类别。

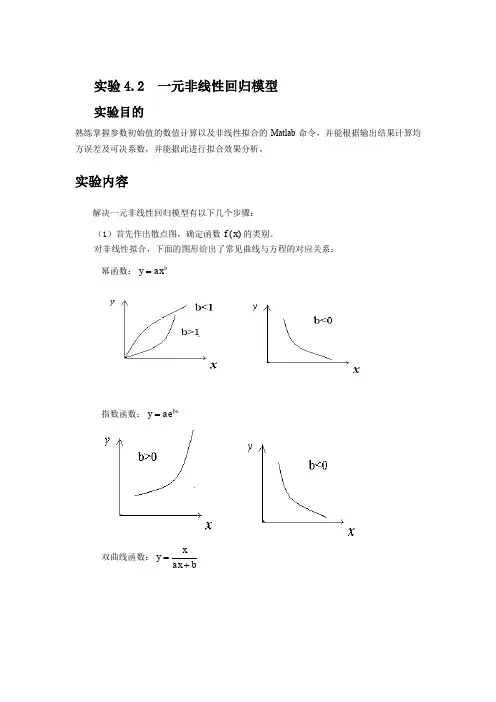
对非线性拟合，下面的图形给出了常见曲线与方程的对应关系： 幂函数：bax y =指数函数：bxae y =双曲线函数：bax xy +=对数函数：x b a y ln +=指数函数：xb ae y =S 形曲线：xbea y -+=1具有S 形曲线的常见方程有： 罗杰斯蒂（logistic ）模型：xey γβα-+=1 龚帕兹（Gomperty ）模型：)ex p(xk e y --=βα理查德（Richards ）模型：δγβα/1)]ex p(1/[x y -+=威布尔(Weibull)模型：)ex p(δγβαt y --=（2）①根据已知数据确定待定参数的初始值。

②正确输入函数。

③利用非线性拟合命令计算最佳参数。

（3）根据可决系数，比较拟合效果。

在Matlab 中进行非线性拟合的命令如下：[b,r,J] = nlinfit(x,y,fun,b0)其中，x,y 为原始数据，fun 是在M 文件中定义的函数，b0是函数中参数的初始值；b 为参数的最优值，r 是各点处的拟合残差，J 为雅克比矩阵的数值.注意：在6.1版本中输入x 是列向量，y 是行向量，而在7.0以上版本要求x ,y 要一致. 【例题4.2】炼钢厂出钢时所用盛钢水的钢包，由于钢水对耐火材料的侵蚀，容积不断增大，我们希望找出使用次数与增大容积之间的函数关系.实验数据如表4.2：表4.2 钢包使用次数与增大容积（1）分别选择函数bax x y +=、)1(cx be a y +=、c bx ax y 2++=、x bae y =拟合钢包容积与使用次数的关系，在同一坐标系内作出函数图形；（2）计算四种拟合曲线的均方差，并以此作为判别标准确定最佳拟合曲线 （3）二次多项式拟合的效果如何？分析内在原因 解：x1=[2:16];y1=[6.42,8.2,9.58,9.5,9.7,10,9.93,9.99,10.49,10.59,10.6,10.8,10.6,10.9,10.76]; b01=[0.1435,0.084]; %初始参数值 fun1=inline('x ./(b(1)+b(2)*x)','b','x'); [b1,r1,j1]=nlinfit(x1',y1,fun1,b01); y=x1./(0.1152+0.0845*x1); subplot(221)plot(x1,y1,'*',x1,y,'-or'); legend('原始数据','y=x/(ax+b)') b02=[112,0.4,0.2]; %初始参数值fun2=inline('b(1)*(1-b(2)*exp(-b(3)*x))','b','x'); [b2,r2,j2]=nlinfit(x1',y1,fun2,b02); f=10.5975*(1-0.9287*exp(-0.4531*x1)); subplot(222)plot(x1,y1,'*',x1,f,'-or');legend('原始数据','y=a(1+bexp(cx)') p=polyfit(x1,y1,2);g= -0.0290*x1.^2+0.7408*x1+6.0927; subplot(223)plot(x1,y1,'*',x1,g,'-or'); legend('原始数据','二次函数') b04=[112,-0.11]; %初始参数值 fun4=inline('b(1)*exp(b(2)./x)','b','x'); [b4,r4,j4]=nlinfit(x1',y1,fun4,b04); h=11.6037*exp(-1.0641./x1); subplot(224)plot(x1,y1,'*',x1,h,'-or'); legend('原始数据','y=aexp(b/x)')51015206810125101520510152068101205101520图4.3 原始数据与四种拟合曲线图为了比较上述四条曲线拟合的效果，我们首先确定如下的评价准则：均方残差)/()ˆ(1512p n y y MSE i i i --=∑=越小越好 其中i y 是原始数据，i yˆ是拟合曲线在i x 处的函数值，n 是原始数据的个数，p 是拟合曲线中参数个数.我们计算均方残差程序如下：[sum(r1.^2)/(15-2),sum(r2.^2)/(15-3),sum((y1-g).^2)/(15-3),sum(r4.^2)/(15-2)]ans = 0.0921 0.0875 0.2306 0.0664由此可知选择函数xbae y 进行拟合效果最好，而多项式的拟合效果最差.其原因在于多项式没有任何渐近线，而从实际问题可知钢包使用的年龄是有限的，因此选择函数应该考虑到其右上方有一条水平渐近线.结果说明：（1）在Matlab6.1版本中输入x 是列向量，y 是行向量，而在7.0以上版本要求x ,y 应同为行向量（或同为列向量）.（2）如果确定初始参数值时遇到复杂的方程组，我们可以根据第三章中介绍的计算方程零点的方法，利用Matlab 计算初始值.【例4．3】表4.3给出了淮南市从1978年到20001年国民生产总值、第一产业、第二产业以及第三产业的数据，根据数据分析解决以下问题：（1）将各指标进行标准化，即减去各自的均值再比上标准差，计算各指标之间的相关系数矩阵；哪两个指标之间具有高度线性关系？（2）利用原始数据建立第一产业与第二产业之间的函数关系，在同一坐标系内作出原始数据与拟合曲线的散点图，计算均方误差、决定系数并预测2002年的第二产业生产总值.（3）利用标准化后的数据解决（2）中的问题，结果是否比用原始数据要好？为什么？表4.3淮南市部分经济指标题目分析：本题的第一问是解决大样本数据的处理问题，利用zscore命令即可解决，而计算指标之间的相关系数矩阵以后，可以获知那些指标之间有较强的线性相关性，若有两个非平稳的经济指标，随着时间的推移各自变化比较复杂，但是两者之间存在长期的均衡关系则可以利用回归分析建立两者之间的函数关系.从相关系数矩阵（表 4.4）和散点图（图4.4）可以看出国民生产总值与各产业都具有较强的线性关系，第一产业与第二产业以及第三产业之间也具有较大的线性相关.计算程序：首先将原始数据输入a=[78258 9230 51827 1720181785 10007 52274 1950487645 10751 55502 2139299072 17263 58182 23627105386 17282 62020 26084118832 20961 66988 30883148277 25755 86215 36307166410 30103 93586 42721189776 35906 101085 52785208477 43335 104604 60538258354 45125 146327 66902284792 52227 164217 68348306605 57351 169721 79533275928 27740 173600 74588351233 55847 200975 94411532686 80047 324491 128148683059 124984 392063 166012834994 135121 472819 2270541063871 154935 603812 3051241187782 169629 644155 3739981203396 178378 603230 4217881238310 187165 595097 4560481259965 174217 586677 4990711348558 170622 638398 539538];z=zscore(a); % 将原始数据标准化corrcoef(a); % 计算各指标的相关系数，得到如下结果表4.4 国民生产总值与各产业的相关系数[b,bint,r,rint,s]=regress(a(1:24,3),[ones(24,1),a(1:24,2)]);作图程序subplot(221),plot(a(1:24,2),a(1:24,3),'x'),legend('一产与二产')subplot(222),plot(a(1:24,1),'-*'),legend('第一产业')subplot(223),plot(a(1:24,3),'-o'),legend('第二产业')t=1:24;y= a(1:24,3);x=a(1:24,2);subplot(224),plot(t,y, '-*',t,3.5*x+2819.4,'-or'),legend('原始','拟合')均方差与可决系数计算程序sum(r.^2)/22,1- sum(r.^2)/sum((y-mean(y)).^2)利用2002年第一产业的产值187438，代入拟合曲线计算出2002年淮南市第二产业生产总值为658850实际数值为740059，相对误差为0.1097图4.4 国民生产总值与第二产业关系结果说明：（1）建立一次函数可以利用多项式回归的命令，本题我们利用了多元线性回归的命令；（2）我们用第一产业的一次函数近似计算第二产业生产总值，得到的绝对误差较大，其中的原因可以从第一产业与第二产业的图形中看出，第一产业在1991年处有一个异常点这是由于该年淮河洪灾造成淮南地区严重减产，而第二产业从1997年开始逐年下降直到2001年才出现上升，因此如果我们选取虚拟变量纠正异常点，或者分段拟合就可以进一步缩小误差。

⼀元⾮线性回归⼀元⾮线性回归有时，回归函数并⾮是⾃变量的线性函数，但通过变换可以将之化为线性函数，从⽽利⽤⼀元线性回归对其分析，这样的问题是⾮线性回归问题。

为了检验X射线得到杀菌作⽤。

⽤200kv的X射线照射杀菌，每次照射6分钟，照射次数为x,照射后所剩的细菌数为y,下表是⼀组试验结果x y x y x y1 783 815415282 621 912916203 433 1010317164 431 117218125 287 12501996 251 13432077 175 1431根据经验知道y关于x的曲线回归⽅程如bxyae试给出具体的回归⽅程，并对其对应的决定系数R^2和剩余标准差s。

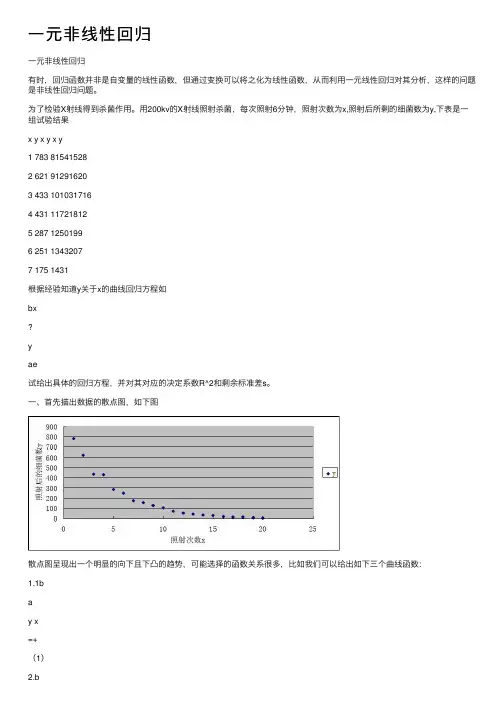
⼀、⾸先描出数据的散点图，如下图散点图呈现出⼀个明显的向下且下凸的趋势，可能选择的函数关系很多，⽐如我们可以给出如下三个曲线函数：1.1bay x=+（1）2.baxy=（2）3.bxy ae=（3）⼆、参数估计1.为了能采⽤⼀元线性回归分析⽅法，我们做如下变换yv ln=u=x则（1）式的曲线图就化为如下的散点图u i∑= 3655 i v ∑=87.22497u =182.75 v =4.3612482ui∑=1611149 u i i v ∑=21281.692nu =667951.3 nuv =15940.36uu l = 943197.8 uv l =5341.3291B =uuuvl l =130.9375 0B=v - B1=-388.301得出⽅程v=-388.301+130.9375x四、结束语对于可化为线性模型的回归问题，⼀般先将其化为线性模型，然后再⽤最⼩⼆乘法求出参数的估计值，最后再经过适当的变换，得到所求回归曲线。

在熟练掌握最⼩⼆乘法的情况下，解决上述问题的关键是确定曲线类型和怎样将其转化为线性模型。

确定曲线类型⼀般从两个⽅⾯考虑:⼀是根据专业知识，从理论上推导或凭经验推测、⼆是在专业知识⽆能为⼒的情况下，通过绘制和观测散点图确定曲线⼤体类型。

第五章回归分析第一节一元线性回归中的参数估第二节一元线性回归中的假设检第三节可线性化的一元非线性回归第四节多元线性回归中的参数估计有时两个变量之间的关系可以不是直线（或线性）的相关关系，而是某种曲线（或非线性）的相关关系。

例1 出钢时所用的盛钢水的钢包，由于钢水对耐火材料的浸蚀，容积不断增大。

我们希望找到使用次数增大的容积之间的关系y 与之间的关系。

x 对一钢包作试验，测得的数据列于下表：表5-2使用次数增大容积使用次数增大容积2 6.421010.498201059x y x y 38.201110.5949.581210.6059.501310.8069.701410.60710.001510.90993107689.931610.7699.99画散点图，从图上我们看到开始浸蚀速度快然后逐渐减慢而从图上我们看到，开始浸蚀速度快，然后逐渐减慢，而x点的分布越来越接近于一条平行于轴的直线，因此钢包容积不会无限增加。

显然，将此例看成一元线性回归是不合适的。

这显然，将此例看成元线性回归是不合适的。

这种需要配曲线的情况就是非线性回归或曲线回归。

此例中应该怎样配曲线呢？配曲线的一般方法如下：先对两个变量和作次试验观察得画出点图根据点图x y n 12，画出点图，根据点图确定需配曲线的类型。

通常选择下面六类曲线之一：(),,1,2,,i i x y i n = （1）双曲线（2）幂函数曲线1ba =+,0,by ax x =>其中0a >y x（3）指数曲线（4）倒指数曲线bxbxy ae=其中0a >y ae=其中0a >（5）对数曲线（6）S 型曲线1=log ,y a b x =+0x >xy a be-+然后，由对试验数据确定每一类曲线的未知参数与n a 。

采用的方法是通过变量代换把非线性回归化成线b 性回归，即采用非线性回归线性化的方法。

下面介绍三类曲线线性化的具体方法三类曲线线性化的具体方法。

.学号姓名学院专业化学工程与技术成绩一元非线性回归分析的应用——以流化床中不同床层高度处的气泡直径为例摘要：一元非线性回归预测法是分析一个因变量与一个自变量之间的非线性关系的预测方法。

在实际现实问题中，变量之间的关系往往都是比较复杂的非线性相关关系。

本文运用一元非线性回归的分析方法，构建了简单的分析模型，求出模型参数，并对分析结果的显著性进行了假设检验，从而了解到流化床中床层高度与气泡直径之间的关系呈非线性相关(双曲线关系)。

正文：一、问题提出鼓泡流化床由于气体和固体之间有较高的传热、传质速率，已广泛应用于工业领域。

气泡是气固鼓泡流化床中一种重要的现象，气泡结构以及流动过程的变化对反应有较大的影响，气泡的出现、聚并、破裂对床层内颗粒的混合和床层浓度、温度的均匀分布有至关重要的作用，因而研究鼓泡流化床内的气泡行为对提高反应器的效率具有十分重要的意义。

二、数据描述流化床中气泡直径与床层高度之间有一定关系，运用这一关系可以根据流化床中床层高度求出气泡直径，下表是实测14对气泡直径与床层高度的数据记录，用一元非线性回归法分析他们之间的关系。

表1 气泡直径u 与床层高度v 的试验数据三、模型建立（1）构建模型由上表中的数据，做出气泡直径u 与相应的床层高度v 数据的散点图，如下图所示.图一 实验数据散点图该图形显示气泡直径u 与相应的床层高度v 之间存在非线性相关关系。

根据图中散点图的特点，选用双曲线1/u=a + b/v作为回归函数来表示气泡直径u 与床层高度v 之间的关系。

y=1/u x=1/v ①则得线性函数 y=a + b*x （2）模型求解由v、u的试验数据去倒数得x, y的数据，见表2。

表2 u, v的试验数据利用上面的数据，按线性回归公式算得x= 0.080311/14=0.005736, y=0.261725/14=0.018695,Lxx=∑xi2-14x2 =0.000106Lyy=∑yi2-14y2 =0.000548Lxy=∑xiyi-14x y=0.00024ß^= Lxy/ Lxx=0.00024/0.000106=2.263298â =y-ß^x =0.018695-2.263298*0.005736=0.005711 得到样本回归直线方程y^=2.263298x+0.005711 ②下图为用excel拟合的直线图图二实验数据拟合图四、检验用相关系数检验法检验上式，对α=0.01，查相关系数临界值，得r0.01 (12) =0.661,由于│r│=│Lxy│/( Lxx Lyy)^1/2 =0.995938>0.661所以线性回归方程②式的作用高度显著。

案例 目标函数可线性化的曲线回归建模与分析1 曲线回归常用的非线性目标函数及其线性化的方法在一些实际问题中，变量间的关系并不都是线性的，那时就应该用曲线去进行拟合. 用曲线去拟合数据首先要解决的问题是回归方程中的参数如何估计? 解决这一问题的基本思路是：对于曲线回归建模的非线性目标函数)(x f y =，通过某种数学变换⎩⎨⎧==)()(x u u y v v 使之“线性化”化为一元线性函数bu a v +=的形式，继而利用线性最小二乘估计的方法估计出参数a 和b ，用一元线性回归方程u b a vˆˆˆ+=来描述v 与u 间的统计规律性，然后再用逆变换⎩⎨⎧==--)()(11u u x v v y 还原为目标函数形式的非线性回归方程. 下面给出常用的非线性函数及其线性化的方法.⑴ 倒幂函数x b a y 1+=令xu y v 1,== ，则bu a v +=.⑵ 双曲线函数 1ba y x=+b<0 b>0线性化方法令xu y v 1,1== ，则bu a v +=.⑶ 幂函数by ax =b<0 0<b<1 b>1 线性化方法令ln v y =，ln u x =，则bu a v +=.⑷ 指数函数bxy ae =函数图象b>0 b<0线性化方法令ln v y =，u x =，则bu a v +=. ⑸ 倒指数函数bxy ae =b>0 b<0线性化方法 令ln v y =，1u x=，则bu a v +=. ⑹ 对数函数ln y a b x =+ 函数图象b>0 b<0线性化方法令v y =，ln u x =，则bu a v +=.⑺ S 型曲线 1x y a be-=+ 函数图象令1v y=，xu e -=，则bu a v +=. 2 曲线回归方程的评价方法对于可选用回归方程形式，需要加以比较以选出较好的方程，常用的准则有： ⑴ 决定系数2R 定义SSTSSER -=12， 称为决定系数. 显然21R ≤.2R 大表示观测值i y 与拟合值ˆi y比较靠近，也就意味着从整体上看，n 个点的散布离曲线较近.因此选2R 大的方程为好. ⑵ 剩余标准差s 定义)2/(-=n SSE s称为剩余标准差.s 类似于一元线性回归方程中对σ的估计. 可以将s 看成是平均残差平方和的算术根，自然其值小的方程为好.其实上面两个准则所选方程总是一致的，因为s 小必有残差平方和小，从而2R 必定大.不过，这两个量从两个角度给出我们定量的概念.2R 的大小给出了总体上拟合程度的好坏，s 给出了观测点与回归曲线偏离的一个量值.所以，通常在实际问题中两者都求出，供使用者从不同角度去认识所拟合的曲线回归. ⑶ F 检验（类似与一元线性回归中的F 检验）)2/(1/-=n SSE SSR F , 其中∑=-=ni i y y SST 12)(，∑=-=ni i i yy SSE 12)ˆ(，SSE SST SSR -=. 3 范例与MATLAB 实现【例6.2】 为了解百货商店销售额x 与流通率（这是反映商业活动的一个质量指标，指每元商品流转额所分摊的流通费用）y 之间的关系，收集了九个商店的有关数据（见下表）.表 销售额与流通费率数据绘制散点图x=[1.5, 4.5, 7.5,10.5,13.5,16.5,19.5,22.5,25.5];y=[7.0,4.8,3.6,3.1,2.7,2.5,2.4,2.3,2.2];sdt(x,y)nlin1(x,y)拟合曲线方程是y=2.2254+7.6213/x剩余标准误差Sy=0.42851可决系数R=0.96733'方差来源' '偏差平方和' '自由度' '方差' ' F值' 'F临界值' '显著性' '回归' [18.7146] [ 1] [18.7146] [101.9186] [ 5.5914] '* *''剩余' [ 1.2854] [ 7] [ 0.1836] [] [12.2464] [] '总和' [ 20] [ 8] [] [] [] []拟合幂函数曲线nlin3(x,y)拟合曲线方程是y=8.5173x^-0.42589剩余标准误差Sy=0.146可决系数R=0.99626'方差来源' '偏差平方和' '自由度' '方差' ' F值' ' F临界值' '显著性' '回归' [19.8508] [ 1] [19.8508] [931.2285] [ 5.5914] '* *''剩余' [ 0.1492] [ 7] [ 0.0213] [] [12.2464] []拟合指数函数曲线nlin5(x,y)拟合曲线方程是y=2.3957exp(1.7808/x)剩余标准误差Sy=0.6497可决系数R=0.92318'方差来源' '偏差平方和' '自由度' '方差' 'F值' ' F临界值' '显著性' '回归' [17.0452] [ 1] [17.0452] [40.3812] [ 5.5914] '* *' ' [ 2.9548] [ 7] [ 0.4221] [] [12.2464] []'剩余拟合对数函数曲线nlin6(x,y)拟合曲线方程是y=1632.5-1.713log(x)剩余标准误差Sy=0.2762可决系数R=0.98656'方差来源' '偏差平方和' '自由度' '方差' ' F值' ' F临界值' '显著性''回归' [19.4660] [ 1] [19.4660] [255.1773] [ 5.5914] '* *'剩余' [ 0.5340] [ 7] [ 0.0763] [] [12.2464] []'总和' [ 20] [ 8] [] [] [] []【说明】函数nlin1，nlin2，nlin3，nlin4，nlin5，nlin6，nlin7分别用来拟合第一（倒幂函数）、二（双曲线）、三（幂函数）、四（指数函数）、五（倒指数函数）、六（对数函数）、七（S型曲线）种类型曲线求非线性回归的回归方程函数，并在同一个图形中绘制散点图和回归线图.这几个函数的调用方式相同，以第一个函数为例[S,Sy,r2,table]=nlin1(x,y)输入参数x,y是长度相等的两个向量.输出参数个数可选如果没有输出参数，则在命令窗口中显示回归线方程,剩余标准误差、可决系数、方差分析表，并绘制散点图和拟合曲线图.如果有输出参数，第一个输出参数是拟合曲线方程.如果有两个输出参数，第二个输出参数是剩余标准误差Sy.如果有三个输出参数，第三个输出参数是可决系数.如果有四个输出参数，第四个输出参数是方差分析表.。

Python数据挖掘—回归—⼀元⾮线性回归1、使⽤scatter_matrix判断个特征的数据分布及其关系散步矩阵(scatter_matrix)Pandas中散步矩阵的函数原理1def scatter_matrix(frame, alpha=0.5, figsize=None, ax=None, diagonal='hist', marker='.', density_kwds=None,hist_kwds=None, range_padding=0.05, **kwds)参数如下：frame:(DataFrame)，DataFrame对象alpha:(float,可选)，图像透明度，⼀般取(0,1]figsize:((float,float),可选)，以英⼨单位的图像⼤⼩，⼀般以元组(width,height)形式设置ax:(Matplotlib axis object,可选)，⼀般取Nonediagonal:({"hist","kde"})，必须只能从这两个中选⼀个，"hist"表⽰直⽅图(Histogram plot)，“kde”表⽰核密度估计(Kernel Density Estimation);该参数是scatter_matrix函数的关键参数marker：（str，可选），Matplotlib可⽤的标记类型，如：‘，’，‘.’，‘o’density_kwds：（other plotting keyword argumentss，可选），与kde相关的字典参数hist_kwds：(other plotting keyword arguments，可选)，与hist相关的字典参数range_padding：（float，可选），图像在x轴，y轴原点附近的留⽩(padding)，该值越⼤，留⽩距离越⼤，图像远离坐标原点kwds:(other plotting keyword argumentss，可选)与scatter_matrix函数本⾝相关的字典参数kde值diagonal参数取’kde’值时，表⽰散布矩阵的对⾓线上的图形为数据集各特征的核密度估计(Kernel DensityEstimation，KDE)。