一元线性回归模型在经济预测中的应用

文献综述信息与计算科学一元线性回归在经济预测中的应用经济预测是指用可靠的方法进行对未来经济的分析，是与未来有关的旨在减少不确定性对经济活动影响的一种经济分析．它是对将来经济发展的科学认识活动．经济预测是以科学的理论和方法、可靠的资料、精密的计算及对客观规律性的认识所作出的分析和判断。

这样的预测是一种分析的程序，它可以重复地连续进行下去。

目的是为未来问题的经济决策服务．为了提高决策的正确性，需要由预测提供有关未来的情报，使决策者增加对未来的了解，把不确定性或无知程度降到最低限度，并有可能从各种备选方案中作出最优决策．因此，经济预测是各级领导机关和经济管理工作者展望经济发展前景，制定政策，编制计划，做出决策，以及进行科学管理的重要依据，在计划经济中有着重要的作用．预测是一门实用学科，它有科学基础，包括理论、资料、方法、计算等因素，依赖于对客观经济规律的认识和掌握。

它还依赖于预测者提出假设、选择方法、利用资料的技巧，和运用他自己的学识、经验、获得的情报进行判断的能力．经济预测有它的哲学基础、经济学基础、统计学基础，同时在多数情况下还以经济数学模型的建立与运用为基础。

一种实用模型根据一定的理论和事实，考虑到种种条件的假设和政策变化的影响，就可以用来预测经济的发展．经济预测的方法一般分为质的预测方法与量的预测方法两大类。

第一类方法，如专家调查法、民意调查法等．后一种方法是向消费者、生产者调查他们对未来发展的意见或意向，考虑他们的心理因素的预测方法．它适用于了解居民的消费需求和购买意图、市场的动向以及投资的趋向等问题．第二类方法，如时间数列法、指标分析法、因素分析法等。

时间数列法是通过分析时间数列的组成要素来研究其变化形态，把过去的发展趋势延续下去和外推未来的预测方法．它的主要方法有移动平均法、加权移动平均法、指数平滑法、最小平方法等等。

指标分析法是通过分析反映经济变动的互有联系的指标或指标组，研究那些预示经济转折的“动向”指标和预报经济可能出现严重问题的“警戒”指标，来确定经济形势变化的迹象的预测方法。

线性回归分析及其在经济预测中的应用线性回归分析是一种常用的统计方法，用于研究自变量与因变量之间的关系。

它假设自变量与因变量之间存在线性关系，并通过拟合一条直线来描述这种关系。

线性回归分析在经济学领域有着广泛的应用，可以用于预测经济指标、分析经济政策的效果等。

首先，线性回归分析可以用于预测经济指标。

经济指标是评估经济状况和发展趋势的重要依据，例如国内生产总值（GDP）、消费者物价指数（CPI）等。

通过收集历史数据，我们可以建立一个线性回归模型，将过去的自变量与因变量进行拟合，然后利用这个模型来预测未来的因变量。

例如，我们可以利用过去几年的GDP增长率和其他相关因素，来预测未来一年的GDP增长率。

这样的预测对政府决策、企业投资等具有重要的指导作用。

其次，线性回归分析可以用于分析经济政策的效果。

在经济学中，政府的经济政策往往会对经济指标产生影响，例如降低利率可以刺激投资，提高税收可以增加政府财政收入等。

通过线性回归分析，我们可以将政策变量与经济指标进行拟合，从而判断政策对经济的影响程度。

例如，我们可以将货币供应量与通货膨胀率进行回归分析，来评估货币政策对通胀的影响。

这样的分析有助于政府制定更有效的经济政策，提高经济运行的稳定性和可持续性。

除了经济预测和政策分析，线性回归分析还可以用于经济学理论的验证和发展。

经济学理论通常会提出一些假设和关系，例如供给与需求之间的关系、劳动力市场的决定因素等。

通过线性回归分析，我们可以将理论中的变量与实际数据进行拟合，从而验证理论的有效性。

如果理论与实际数据拟合较好，那么就可以认为该理论在一定程度上解释了经济现象。

如果理论与实际数据拟合较差，那么就需要对理论进行修正或者寻找其他解释。

这样的研究有助于推动经济学理论的发展，提高其解释和预测能力。

然而，线性回归分析也存在一些限制和局限性。

首先，线性回归分析假设自变量与因变量之间存在线性关系，但实际情况往往更为复杂。

如果变量之间存在非线性关系，那么线性回归模型的拟合效果可能较差。

线性回归模型在社会科学中的应用在社会科学领域，线性回归模型是一种经济、心理学、社会学等学科中常用的统计分析工具。

线性回归模型能够提供变量之间的关联性和预测能力，对于研究人类行为和社会现象具有重要的应用。

下面将介绍线性回归模型在社会科学中的应用，并探讨其局限性和改进方向。

一、经济领域中的线性回归模型应用在经济学中，线性回归模型被广泛运用于经济现象的解释和预测。

例如，通过构建家庭收入与教育水平的线性回归模型，可以分析收入与教育之间的关系。

该模型可以帮助政府了解教育资源的投入效果，制定有针对性的教育政策。

此外，线性回归模型还可以用于研究物价与供求关系、经济增长与人口因素之间的关系等。

二、心理学中的线性回归模型应用心理学家常常使用线性回归模型来探索人类行为和心理现象之间的关系。

例如，通过构建社会支持与幸福感的线性回归模型，可以了解社会支持对个体幸福感的影响程度。

此外，线性回归模型还可以用于研究人格特征与工作表现之间的关系、家庭环境对儿童心理发展的影响等。

三、社会学中的线性回归模型应用社会学研究中，线性回归模型被广泛应用于社会现象的解释和预测。

例如，通过构建收入与社会阶层的线性回归模型，可以研究社会阶层对个体经济状况的影响。

此外，线性回归模型还可以用于研究种族、性别对职业选择和收入差距的影响等。

尽管线性回归模型在社会科学中具有广泛的应用，但也存在一些局限性。

首先，线性回归模型假设自变量和因变量之间的关系是线性的，但实际情况往往更为复杂。

其次，线性回归模型对数据的要求较高，需要满足一系列假设条件，如自变量和误差项之间应独立、误差项应服从正态分布等。

此外，线性回归模型容易受到离群值（outliers）的影响，进而导致模型拟合效果不佳。

为了克服线性回归模型的局限性，研究者们提出了一系列改进方法。

例如，非线性回归模型可以用于处理自变量与因变量之间的非线性关系。

加权最小二乘法和岭回归等方法可用于处理数据不满足线性回归模型的假设条件的情况。

线性回归模型在金融领域中的应用探讨一、引言随着金融市场的不断发展和金融数据的快速增长，如何从海量数据中提取有效的信息成为金融领域研究的热点问题之一。

线性回归模型作为一种重要的统计分析工具，已经被广泛应用于金融领域中的数据分析和预测，如股票价格预测、信用评级、风险控制等。

本文将从金融市场分析的角度，探讨线性回归模型在金融领域中的应用情况及其优缺点。

二、线性回归模型的基本原理线性回归模型是一种用于描述自变量与因变量之间关系的数学模型。

简单线性回归模型可以表示为：$Y_i = \beta_0 + \beta_1 X_i + \epsilon_i$其中，$Y_i$是因变量，$X_i$是自变量，$\beta_0$和$\beta_1$是待求系数，$\epsilon_i$是误差项。

通过对样本数据的拟合，可以得到模型的系数估计值，从而进行预测和分析。

三、线性回归模型在金融领域中的应用1. 股票价格预测股票价格预测一直是金融领域中的热点问题。

通过构建一个合理的模型，可以对未来的股票价格进行预测，为投资者提供决策依据。

线性回归模型可以结合资本市场理论，考虑到影响股票价格的各种因素，如宏观经济环境、公司业绩、市场情况等，来进行股票价格的预测。

2. 信用评级信用评级是金融领域中的重要工作之一。

应用线性回归模型，可以将不同的客户的历史信用数据作为自变量，将客户当前的信用水平作为因变量，从而构建出一个评级模型。

评级模型可以根据客户的信用等级，给出相应的贷款利率或者借款额度等信息，对于银行和其他金融机构来说，可以进行更为准确的风险控制。

3. 风险控制风险控制是金融机构必须考虑的问题。

线性回归模型可以通过对历史数据进行分析，推断出不同的因素对风险的影响程度，从而建立出相应的模型。

模型可以预测未来的风险水平，为金融机构的风险控制提供决策依据。

四、线性回归模型的优缺点线性回归模型具有简单易懂、操作便捷、可解释性强的优点。

此外，线性回归模型还可以通过引入新的解释变量，来不断改进和修正模型。

线性回归模型在经济学中的应用线性回归是一种经典的统计学方法，广泛应用于经济学研究中。

线性回归模型的基本理念是建立一个最小二乘回归方程，从而解释研究对象之间的相互关系。

在经济学研究中，线性回归被广泛运用于生产函数、消费函数、投资函数、需求曲线等领域的研究。

本文将就线性回归模型在经济学中的应用进行阐述。

```一、生产函数与线性回归模型生产函数是指在一定时间内，生产者用特定的投入品组合生产出最大产量的函数关系。

生产函数研究的是如何用投入品的组合来最大限度地提高产出。

生产函数通常可以使用线性回归模型进行分析。

线性回归模型的一般形式为：y=b+ kx+ e，其中y表示因变量，x表示自变量，b为截距，k为斜率，e表示误差项。

在生产函数分析中，自变量表示生产投入，例如，劳动力、资本等，因变量表示输出效果，例如，产量。

生产函数可以用多元线性回归模型表示，包括所有的生产投入，例如，人力投入、资本投入、土地、原材料等。

这些因素的权重可以通过线性回归模型来计算。

二、消费函数与线性回归模型消费函数是指消费者在一定收入和价格条件下购买某种商品或服务的数量与价格的关系函数。

消费函数分析可以应用线性回归模型。

线性回归模型可以帮助研究人员确定消费者收入和价格对消费量的影响。

一般而言，较高的收入和较低的价格会导致更高的消费量。

通过回归分析，可以提供有关收入和价格与消费之间的程度和方向关系的定量估计。

消费函数的估算可以帮助企业和政府确定市场需求，以便制定更为合理的产品价格。

三、投资函数与线性回归模型投资函数是指投资者在一定经济条件下，投入资产获得的投资回报率。

在经济学中，投资是推动经济发展的主要驱动力之一。

投资函数可以应用线性回归模型。

线性回归模型可以帮助分析投资者在资产配置时面临的机会和风险，以及投资回报率与其他生产因素的关系。

投资函数模型可以利用历史数据，包括过去的经济周期、工业生产、人均收入等，建立预测模型和决策模型，以支持投资者做出更为精准的投资决策。

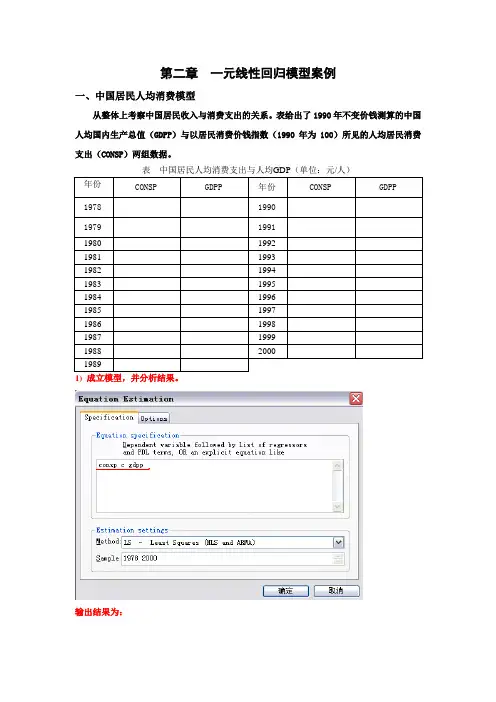
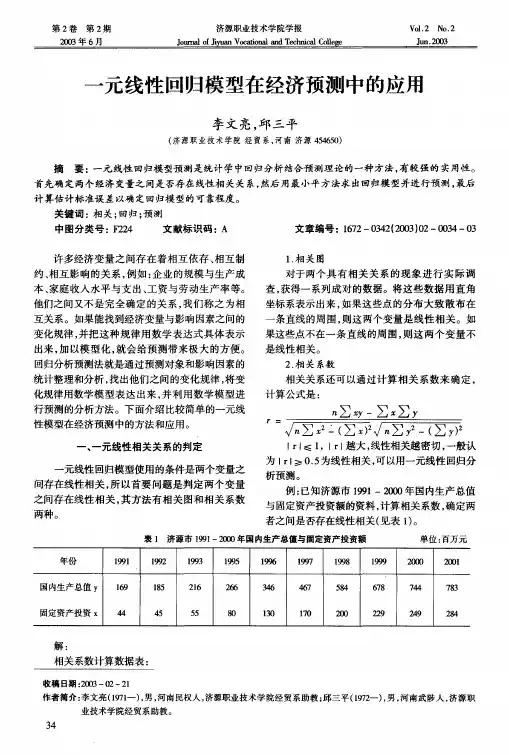
第二章一元线性回归模型案例一、中国居民人均消费模型从整体上考察中国居民收入与消费支出的关系。

表给出了1990年不变价钱测算的中国人均国内生产总值（GDPP）与以居民消费价钱指数（1990年为100）所见的人均居民消费支出（CONSP）两组数据。

表中国居民人均消费支出与人均GDP（单位：元/人）年份CONSP GDPP年份CONSP GDPP19781990197919911980 19921981 19931982 19941983 19951984 19961985 19971986 19981987 19991988 200019891) 成立模型，并分析结果。

输出结果为：对应的模型表达式为：=+201.1070.3862CONSP GDPP20.9927,2859.23,0.55===R F DW从回归估量的结果能够看出，拟合度较好，截距项和斜率项系数均通过了t查验。

中国人均消费增加10000元，GDP增加3862元。

二、线性回归模型估量表给出黑龙江省伊春林区1999年16个林业局的年木材采伐量和相应砍木剩余物数据。

利用该数据（1）画散点图；（2）进行OLS回归；（3）预测。

表年剩余物y林业局名年木材剩余物y t（万m3）年木材采伐量x t（万m3）乌伊岭东风新青红星五营上甘岭友好翠峦乌马河美溪大丰南岔带岭朗乡桃山双丰合计（1）画散点图先输入横轴变量名，再输入纵轴变量名得散点图（2）OLS估量弹出方程设定对话框取得输出结果如图：由输出结果能够看出，对应的回归表达式为：ˆ0.76290.4043t t yx =-+20.9129,146.7166, 1.48R F DW === （3）x=20条件下模型的样本外预测方式 第一修改工作文件范围将工作文件范围从1—16改成1—17确信后将工作文件的范围改成包括17个观测值，然后修改样本范围将样本范围从1—16改成1—17打开x的数据文件，利用Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改成17—17，即只预测x=20时的y的值。