实验四 核衰变的统计规律与放射性测定的实验数据处理
- 格式:doc
- 大小:258.00 KB
- 文档页数:6

实验二 核衰变的统计规律实验人:*** 合作者:*** 实验时间:2011/06/03一、引言对核衰变产生的射线可用计数方式测量。
然而多次测量相同时间间隔内的计数,即使保持相同的实验条件,每次测量的结果并不相同,而是围绕某一平均值上下涨落,反映出核衰变的随机性二、实验目的1、了解并验证原子核衰变及放射性计数的统计性2、了解统计误差的意义,掌握计算统计误差的方法3、学习检验测量数据的分布类型的方法三.原理1.放射性测量的随机性和统计性在做重复的放射性测量中,即使保持完全相同的实验条件(例如放射性的半衰期足够长,因此在实验时间内可以认为其强度基本上没有变化;源与计数器的相对位置始终保持不变;每次测量时间不变;测量仪器足够精确,不会产生其它的附加误差等等),每次的测量结果并不完全相同,而是围绕其平均值上下涨落,有时甚至有很大的差别,也就是说物理实验的测量结果具有偶然性,或者说随机性。
物理测量的随机性产生原因不仅在于测量时的偶然误差,而且更是物理现象(当然包括放射性核衰变)本身的随机性质,即——物理量的实际数值时刻围绕着平均值发生微小起伏。
在微观现象领域,特别是在高能物理实验中,物理现象本身的统计性更为突出。
按照量子力学的原理,对处于同一个态的微观粒子,测量同一个可观测的物理量时,即使不存在任何测量误差,各次测量结果也会不同,除非粒子处于这个可观测量的本征态;比如同一种粒子的寿命,其实测值分布在从相当短到相当长的范围内。
另一方面,所谓偶然的东西,是一种有必然性隐藏在里面的形式;我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。
2.核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。
放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,与其他原子核是否衰变无关;因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。
在N 0个原子核的体系中,单位时间内对于每个原子核来说只有两种可能:A 类是原子核发生衰变,B 类是没有发生核衰变。

第一部分G-M计数器【实验目的】1、了解G_M计数器的工作原理,掌握其基本性能及测试方法。
2、学会正确使用G-M计数器的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M计数器系统输出回路参数。
【实验内容】1.在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参数并选择工作电压。
2.用示波器测定G-M计数器的分辨时间。
3.观察并记录G-M管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
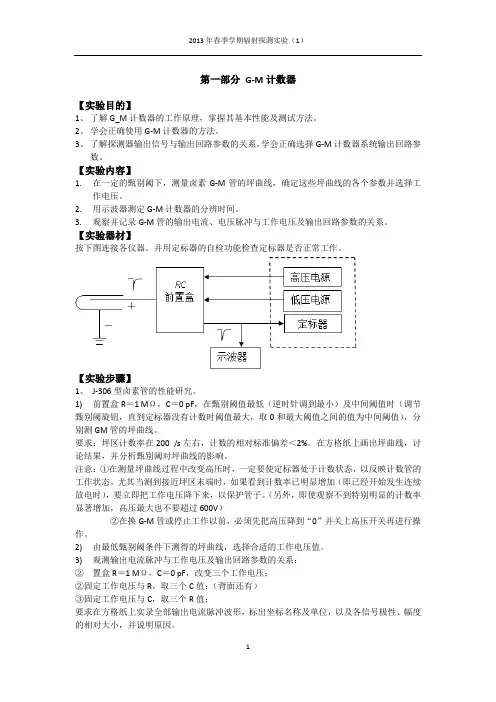
【实验器材】按下图连接各仪器。
并用定标器的自检功能检查定标器是否正常工作。
【实验步骤】1、J-306型卤素管的性能研究。
1) 前置盒R=1 MΩ,C=0 pF,在甄别阈值最低(逆时针调到最小)及中间阈值时(调节甄别阈旋钮,直到定标器没有计数时阈值最大,取0和最大阈值之间的值为中间阈值),分别测GM管的坪曲线。
要求:坪区计数率在200 /s左右,计数的相对标准偏差<2%。
在方格纸上画出坪曲线,讨论结果,并分析甄别阈对坪曲线的影响。
注意:①在测量坪曲线过程中改变高压时,一定要使定标器处于计数状态,以反映计数管的工作状态。
尤其当测到接近坪区末端时,如果看到计数率已明显增加(即已经开始发生连续放电时),要立即把工作电压降下来,以保护管子。
(另外,即使观察不到特别明显的计数率显著增加,高压最大也不要超过600V)②在换G-M管或停止工作以前,必须先把高压降到“0”并关上高压开关再进行操作。
2) 由最低甄别阈条件下测得的坪曲线,选择合适的工作电压值。
3) 观测输出电流脉冲与工作电压及输出回路参数的关系:②置盒R=1 MΩ,C=0 pF,改变三个工作电压;②固定工作电压与R,取三个C值;(背面还有)③固定工作电压与C,取三个R值;要求在方格纸上实录全部输出电流脉冲波形,标出坐标名称及单位,以及各信号极性、幅度的相对大小,并说明原因。
注意:①中的三个电压值必须在坪区范围内;为观察到形状较好的电流和电压波形,②、③及以下各步骤中的工作电压可比步骤(2)中选择的工作电压低,具体数值可以取R =1 M Ω,C =0 pF 时,示波器观察电流或电压波形不出现饱和的最大工作电压值。

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是气体探测器的一种,用來测定射线强度,既单位时间的粒子个数。
近年 来,随着闪烁探测器及半导体探测器的发展,其重耍性有所下降,但由于它的没备简单,使 用方便,在有关的放射性测撒屮仍在广泛使用。
一、 实验目的掌握G-M 计数器的工作难础,测定其有关特性,学会使用;以G-M 计数器米测试设备,验 证核袞变的统计规律;学会使川放射性测3结果的误差表示法,学会多次测呈结果的误差计 算及测试吋间的选择。
二、 实验原理1、G-M 计数器原理:G-M 计数器是利用射线使计数管内的丁.作气体电离,然后收集产生的电荷来记录射线的 探测器。
玻璃管内冇糾筒状阴极,在明极对称轴上.装冇丝状阳极。
先将管内抽成真空,冉充入一定s 的惰性气体和少量猝灭气体(卤素或奋机物)在G-M 计数管两级加上电压,没其阳极半 径为a ,阴极半径为b ,阳极与叨极间的电压为U ,则沿着管径向位置为r 处的电场强度 为 ,可见随着r 减小,电场强度增大,且阳极附近急剧增大。
2、脉冲原理(丨)当射线进入G-M 管中使得管中气体电离后,正离子和负离子在管内电场的作川下分 别14阴极和阳极移动。
在阳极附近强人的电场作川K,电子获得强人的动能以至于将阳极附 近的气体电离。
经过多次碰撞,殃及附近的电子急剧增多,形成了 “雪劢电子”;在这些碰 撞中会产生大S 的紫外线光了,这些光了能进一步的产生第二波的“雪崩”效应,增加电了。
这个电子不断培加的过程称为气体放大。
(2) 雪崩过程发屮在殃及附近,加上电子的质量远远小于阳离子的质量,速度比阳离子快, W 此电子很快被阳极吸收,在管内留下一个被大量HI 离子构成的叩离子鞘包围着的叩极。
正 离子鞘将随着电离的发生逐渐增厚,由于正离子鞘的作用,阳极附近的电场将随之减小,以 致新电子无法增殖,即电场强度不足以引发雪崩效应,雪崩效座停止,正离子鞘停止生成, 放电便终止了,何候,正离子鞘在屯场的作用下慢慢移向阴极,最后到达阴极被中和,阳极 附近的电场也随之恢复,使得与G-M 串联的电阻记录下一个电压脉冲。

实验一核衰变与放射性计数的统计规律第一部分 G-M计数器一.实验目的1、了解G-M管的工作原理,掌握其基本性能及其测试方法。
2、学会正确使用G-M管计数装置的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M管计数系统输出回路参量。
二.实验内容1、在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参量并选择工作电压。
2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。
3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
三.实验原理1、G-M管是一种气体探测器。
当带电粒子射入其灵敏体积时,引起气体原子电离。
电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离,即触发“自持放电”。
这一过程产生的电子和正离子向两极漂移时,在外回路产生脉冲信号。
2、从G-M管的工作机制可以看出,入射带电粒子仅仅起一个触发放电的作用,G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关,只和计数管的几何参量、工作电压以及输出回路参量有关。
在G-M管的使用中,坪特性是其最重要的性能之一。
坪特性是判断管子好坏的主要依据,也是选择管子工作电压的依据。
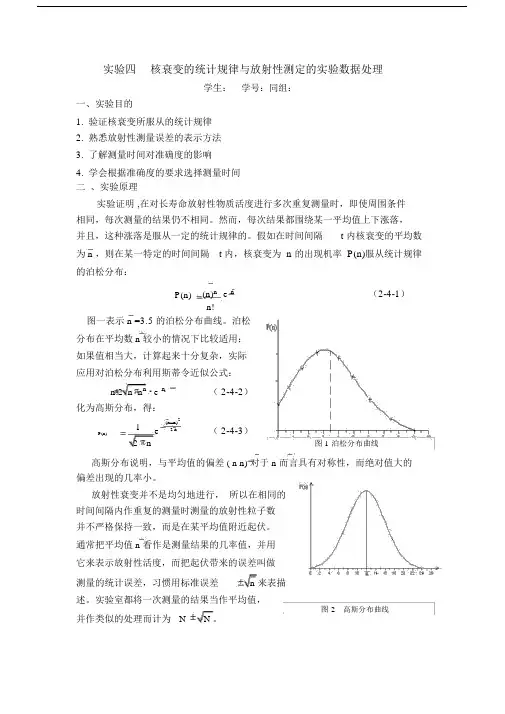
坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时,计数管的计数率随工作电压变化的曲线,见图1-1。
图1-1 G-M计数管的坪曲线表征坪特性的参量主要有:起始电压(Vs):即计数管开始计数时的电压。
坪长: B A =V -V 坪长(单位:百伏) (1-1) 这是管子的工作区域,工作电压一般可选在坪区的21~31的范围内。
坪斜:()100% ()2B A B A B A n n n n V V -=⨯+-坪斜(单位:%/百伏) (1-2) 坪斜主要是由假计数引起的,当然它的值越小越好。
当工作电压高于B V 时,曲线急剧上升,表明管子内发生了持续放电,这会大大缩短管子的寿命,因此在使用中必须注意避免这种情况。
实验四核衰变的统计规律与放射性测定的实验数据处理学生:学号:同组:一、实验目的1.验证核衰变所服从的统计规律2.熟悉放射性测量误差的表示方法3.了解测量时间对准确度的影响4.学会根据准确度的要求选择测量时间二、实验原理实验证明 ,在对长寿命放射性物质活度进行多次重复测量时,即使周围条件相同,每次测量的结果仍不相同。
然而,每次结果都围绕某一平均值上下涨落,并且,这种涨落是服从一定的统计规律的。
假如在时间间隔t 内核衰变的平均数为 n ,则在某一特定的时间间隔t 内,核衰变为 n 的出现机率 P(n)服从统计规律的泊松分布:P(n)(n)n e n(2-4-1)n!图一表示 n =3.5的泊松分布曲线。
泊松分布在平均数 n 较小的情况下比较适用;如果值相当大,计算起来十分复杂,实际应用对泊松分布利用斯蒂令近似公式:n!2 n n n e n( 2-4-2)化为高斯分布,得:1(n n)2e 2 n( 2-4-3)P(n)2n图 1 泊松分布曲线高斯分布说明,与平均值的偏差 ( n n) 对于 n 而言具有对称性,而绝对值大的偏差出现的几率小。
放射性衰变并不是均匀地进行,所以在相同的时间间隔内作重复的测量时测量的放射性粒子数并不严格保持一致,而是在某平均值附近起伏。
通常把平均值 n 看作是测量结果的几率值,并用它来表示放射性活度,而把起伏带来的误差叫做测量的统计误差,习惯用标准误差n 来表描述。
实验室都将一次测量的结果当作平均值,图 2高斯分布曲线并作类似的处理而计为N N 。
计数的相对标准误差为:N1(2-4-4)N N它能说明测量的准确度。
当N 大时,相对标准误差小,而准确度高。
反之,则相对标准误差大,而准确度低。
为了得到足够计数N 来保证准确度,就需要延长测量时间t 或增加相同测量的次数m。
根据计算可知,从时间t 内测的结果中算出的计数率的标准误差为:N N n(2-4-5)t t2t计数率的相对标准误差 E 用下式表示:n1E t(2-4-6)ntn若实验重复进行 m 次,则平均计数率的标准误差等于:n( 2-4-7)mt考虑本底后,标准误差为:N c N b n c n b(2-4-8)t c2t b2t c t bN c为 t c时间内源加本底的计数,n b为 t b时间内本底的计数, n c为源加本底的计数率, n b为本底的计数率。


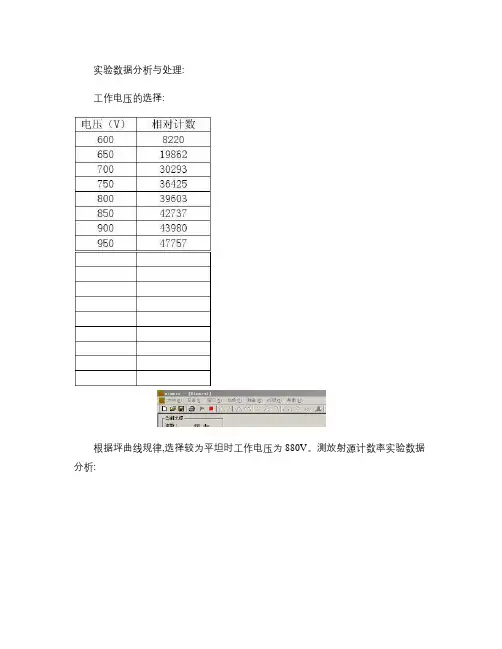
实验数据分析与处理:工作电压的选择:根据坪曲线规律,选择较为平坦时工作电压为880V。
测放射源计数率实验数据分析:实验分析:1. 探测器与放射源的几何位置应保持合理(两者不宜离开太远2.实验中要保证不触碰探测仪,因为本实验是一种强度测量,所以一切有可能影响探测器探测效率的因素都必须严格保持不变,如工作点要保持稳定探测器和源的几何位置也不可以改变。
3.实验数据分析时,软件曾出现提示框显示:“已超出正态分布范围,无法分析”的字样。
打开实验数据后发现实验的第一个数据与之后的数据相去甚远(后面数据均维持在3300~3500范围内,第一个数据为20000+的值,在去除第一个数据后分析实验,软件得以成功分析。
可能由于电压值发生一定变化导致第一个数据出现一定问题,须删除无效数据后进行数据处理。
思考题1.什么是坪曲线?谈谈坪曲线的测量在研究核衰变统计规律实验中的意义? 答:坪曲线是入射粒子的强度不变时,计数器的计数率随工作电压变化的曲线。
测定坪曲线是为了选择一个合适的工作电压,以减少电压漂移对实验的影响.工作点若选在坪区,即使仪器和探头的性能都有变化,也可使总计数率保持稳定。
所以应在曲线较平的部分以及源计数率高本底计数率相对较低处选择工作电压。
2.什么是放射性核衰变的统计性?它服从什么规律?答:放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,与其他原子核是否衰变无关;因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。
其统计分布满足一定的规律性,称此规律性为核衰变的统计性,它服从正态分布。
3.σ的物理意义是什么?以单次测量值N 来表示测量值时,为什么是N N ±?其物理意义又是什么?答:σ的物理意义是在相同条件下作重复测量时,每次测量结果围绕着平均计数值的一个涨落大小。
在实际运算中由于出现概率较大的计数值与平均值N 的偏差不大,我们可以用N 来代N ;因此对于单次测量值N ,可以近似地说在N N ±范围内包含真值的概率是68.3%,这样一来用单次测量值就大体上确定了真值的范围。

实验10-2 核衰变的统计规律【实验目的】1.测量NaI(Tl)闪烁探测器的坪曲线,确定合适的工作电压;指导:用闪烁探测器测量强度不变的放射源时,改变光电倍增管的高压,计数率也会随之改变;原因在于任何一种射线在闪烁探测器中产生的脉冲幅度都不会完全一样,输出脉冲的幅度也分布在一定范围内。
尽管如此,只要射线的能量不是特别低而探测器的工作状态又选择得当,绝大部分信号脉冲都会比光电倍增管的噪声脉冲大。
当电压足够高,信号脉冲幅度基本上都超过了仪器的甄别阈而绝大部分噪声的幅度又还比甄别阈小很多时,随着高压的增加计数率的增加就很缓慢了,这时就出现了“坪区”。
在实验中,重要的是向学生说明在许多核物理实验中测量坪曲线的意义何在。
在本实验中,由于高压相对比较稳定,因此我们在实践中发现选取坪曲线较为平坦(计数率随高压漂移变化较小)的工作点和坪曲线较为陡峭的工作点两者的差异不大。
2.了解并验证原子核衰变及放射性计数的统计性;指导:本实验通过反复测量放射源(137Cs 或60Co )在一段时间内强度并作为一个随机事件,取一个样本容量为A 的样本来观察其结果是否符合正态分布。
当然,源的强度本身随时间衰减,但137Cs 的半衰期长达30年,可以近似认为在实验时间内(大约1——2小时)源强不变。
3.了解统计误差的意义,掌握计算统计误差的方法;指导:这一实验需要一定的概率论和数理统计方面的基础,比如二项式分布、泊松分布、正态分布以及样本均值、样本方差、样本方差的无偏估计;学生应该已经学习过相关课程,若没有接受过类似训练,实验讲义的原理部分已经列出了所需知识。
需要说明的是: 鉴于A x x Ai i /)(12∑=-不是方差2S 的无偏估计,)1/()(12--∑=A x x Ai i 才是,因此取)1/()(12--=∑=A x x S Ai ix 作为样本标准差的无偏估计。
(参见任一概率论数理统计教材) 4.学习检验测量数据的分布类型的方法。

放射性衰变的实验观察与分析实验观察与分析:放射性衰变放射性衰变是指一种原子核自发地发射出射线,从而转变成另一种元素或同位素的现象。
在这个实验中,我们对一种放射性物质的衰变进行了观察与分析。
实验设备与材料:1. 放射性样品(已知是铀)2. 探测器3. 电子计数器4. 实验记录表格实验步骤:1. 将放射性样品放置在探测器旁边,并将探测器连接到电子计数器上。
2. 开始记录计数器每隔一段时间(比如5分钟)所测得的粒子数目,并将其填写在实验记录表格中。
观察与结果:在实验过程中,我们观察到计数器每隔一段时间就会记录到一定数量的粒子。
最初的数目较多,随着时间的推移,记录到的粒子数目逐渐减少,但并未完全消失。
这是因为放射性衰变是一个随机的过程,每个原子核发生衰变的概率是相同的,但时间上的分布是不确定的。
根据粒子数目的变化曲线,我们可以看到一些规律。
一开始,衰变速率很快,数目下降得很快。
但随着时间的推移,衰变速率逐渐减慢,说明衰变速率是逐渐减小的。
这是因为随着原子核数量的减少,相互碰撞的概率也减小,从而导致衰变速率的减缓。
然而,即使在很长时间之后,仍然会记录到一些粒子,这说明放射性衰变是一个持久的过程,不会完全停止。
分析与讨论:根据实验结果,我们可以通过衰变速率的变化来推断放射性物质的半衰期。
半衰期是指在一半的放射性原子核衰变所需的时间。
通过观察衰变速率逐渐减慢的趋势,我们可以估算出半衰期的大致大小。
此外,还可以通过观察放射性衰变产生的射线类型来进一步确认放射性物质的性质。
射线的类型包括阿尔法粒子(α粒子)、贝塔粒子(β粒子)和伽马射线(γ射线)。
通过分析这些射线的能量和穿透能力,可以确定放射性物质的具体类型和原子核的结构。
需要注意的是,放射性衰变是一个存在一定风险的实验。
对于放射性物质的处理和测量需要符合安全操作规程,并使用适当的防护设备。
总结:通过对放射性衰变的实验观察与分析,我们可以了解放射性物质的特性,并且可以通过衰变速率的变化推断出物质的半衰期。
所谓“雪崩”电子;在这些碰撞中会产生大量紫外线光子, 这些光子能够进一步地近代物理实验实验报告盖革-弥勒计数器及核衰变的统计规律同组者:****操作人员:*** .号. *******一.实验仪器:G-M 计数器,3粒子放射源,脉冲示波器。
二•实验原理:1. G-M 计数器原理:高压电源定量惰性气体和少量猝灭气体(卤素或有机物)在G-M 阳极半径为a ,阴极半径为b ,则沿着管径向位置为r 处的电场强度为E=V 。
见随着r 减小,电场强度增大,且在阳极附近急剧增大。
2. 脉冲原理:1. )当射线进入G-M 管中使得管中气体电离后,正离子和负离子在管内电场的作用下分别向阴极和阳极移动。
在阳极附近强大的电场作用下,电子获得极大的动能定标器G-M 计数管玻璃管内有圆筒状阴极, 在阴极对称轴上装有丝状阳极。
先将管内抽成真空,再冲入一计数管两极加上电压/In(a/b)可以至于将阳极附近的气体电离。
经过多次碰撞,阳极附近的电子急剧增多,形成了产生第二波的“雪崩”效应,增加电子。
这个电子不断增多的过程成为气体放大。
2. )雪崩过程发生在阳极附近,加上电子的质量远远小于阳离子的质量,因此电子很快被阳极吸收,在管内留下一个由大量阳离子构成的阳离子鞘包围着阳极。
之减小,直到电场强度不足以引起雪崩效应, 这时雪崩效应停止, 阳离子鞘停止生成,G-M 管进入恢复过程。
在电场的作用下,正离子鞘缓慢地向阴极移动,阳极附近的电场也随之恢复,使得与 G-M 管串联的电阻记录下一个电压脉冲。
3.)当阳离子到达阴极时会再次打出光电子, 如果这些电子再次形成离子放电的话,一个入射粒子就将产生多个信号了。
为了避免再次形成雪崩效应, 使得一个入射粒子只产生一个信号,在管内加入少量的卤素气体来吸收这部分电子。
3. 脉冲特性:1. )坪曲线盖革计数器的计数率与电压有“坪”;在 VC 之后,计数率随着电压急速增大。
2. )电源电压越大,负脉冲幅度越大;串联电阻越大,脉冲宽度较宽,幅度也较大。
衰变统计规律衰变统计规律:在放射性衰变过程中,对于某个特定的放射性核素,其衰变的发生是完全随机且不可预测的,但从大量的原子核来看,其衰变又呈现出一定的统计规律,即在某一固定时间段内,发生衰变的原子核数目是相对稳定的。
嘿,想象一下,这些放射性原子核就像是一群调皮的小精灵,它们可不会乖乖地按照我们期望的方式行动。
它们什么时候衰变,那完全是看它们自己的心情,没有任何规律可循,特别任性!但神奇的是,当把它们聚在一起形成一个庞大的群体时,它们的行为又好像被一只无形的大手给规范住了。
就好像这些小精灵在玩一个特别的游戏,每个小精灵都有可能随时“出局”,也就是发生衰变。
单个小精灵的行为是完全无法预料的,它可能下一秒就“出局”了,也可能等了好久都不“出局”。
但是呢,如果有一大群这样的小精灵,我们就会发现,在一段时间内,总会有差不多固定数量的小精灵“出局”。
这就好像它们虽然各自为战,但冥冥之中又遵循着某种神秘的规则。
比如说铀这种放射性元素吧,它的原子核就一直在玩着这个衰变的游戏。
在一大块铀矿石中,每时每刻都有铀原子核在发生衰变,但我们无法确切地知道下一个衰变的会是哪一个。
然而,通过长时间的观察和统计,我们可以大致算出在一定时间内会有多少铀原子核发生衰变。
这就像是我们虽然不知道彩票的中奖号码是多少,但我们可以通过统计数据大致了解到中奖的概率有多大。
而且啊,这种衰变统计规律在很多领域都有着重要的应用呢。
在核物理学中,科学家们通过研究这种规律来深入了解原子核的结构和性质;在医学上,利用放射性同位素的衰变规律可以进行疾病的诊断和治疗,比如放射性治疗癌症,就是根据衰变规律来精确控制辐射剂量的。
总之,衰变统计规律虽然听起来很神秘,但它却在我们的生活和科学研究中发挥着重要的作用。
它让我们对这个世界的认识更加深入,也为我们解决各种问题提供了有力的工具。
如果你对这些神奇的科学规律感兴趣,不妨去看看相关的科普书籍,或者上网搜索一些专业的科学网站,那里有更多有趣的知识等待着你去探索。
放射性衰变的规律与计算方法在我们生活的这个世界中,存在着许多神秘而又奇妙的现象,放射性衰变就是其中之一。
放射性衰变是指不稳定的原子核自发地放出射线,转变为另一种原子核的过程。
这一过程不仅在科学研究中具有重要意义,也在许多实际应用中发挥着关键作用,比如医疗、能源和考古等领域。
放射性衰变有着其独特的规律。
首先,它是一个随机的过程。
这意味着我们无法准确预测某个原子核在何时会发生衰变,但在大量原子核的集合中,衰变的发生却遵循着一定的统计规律。
就好像抛硬币,每次抛硬币的结果是正面还是反面是无法预测的,但抛很多次后,正面和反面出现的概率会趋近于相等。
对于放射性衰变来说,也是如此。
放射性衰变的速率通常用半衰期来描述。
半衰期是指放射性原子核数目衰变掉一半所需要的时间。
不同的放射性核素具有不同的半衰期,有的短至几毫秒,有的则长达数十亿年。
例如,碘-131 的半衰期约为 8 天,而铀-238 的半衰期则长达约 45 亿年。
放射性衰变主要有三种类型:α衰变、β衰变和γ衰变。
α衰变是指原子核放出一个α粒子(由两个质子和两个中子组成),从而转变为另一种原子核。
β衰变则分为β⁺衰变和β⁻衰变。
β⁺衰变时,原子核中的一个质子转变为一个中子,并放出一个正电子和一个中微子;β⁻衰变时,原子核中的一个中子转变为一个质子,并放出一个电子和一个反中微子。
γ衰变一般不改变原子核的质子数和中子数,只是原子核从激发态跃迁到基态时放出γ射线。
那么,如何计算放射性衰变呢?这就需要用到一些数学公式和方法。
假设初始时刻放射性原子核的数目为 N₀,经过时间 t 后,剩余的原子核数目为 N,放射性衰变遵循指数衰减规律,可以用以下公式表示:N = N₀ × e^(λt)其中,λ 被称为衰变常数,它与半衰期 T₁/₂的关系为:λ = ln2 /T₁/₂。
通过这个公式,我们就可以计算在任意时刻剩余的放射性原子核的数目。
例如,如果我们知道某种放射性核素的半衰期为 10 天,初始时有1000 个原子核,经过 20 天,剩余的原子核数目是多少呢?首先,我们计算衰变常数λ = ln2 / 10 。
第1篇一、实验目的1. 理解核物理的基本概念和原理。
2. 掌握放射性衰变的规律。
3. 学习使用核物理实验仪器。
4. 培养实验操作技能和数据分析能力。
二、实验原理核物理是研究原子核结构、性质和相互作用的学科。
本实验主要通过测量放射性衰变,了解放射性衰变的规律和基本性质。
放射性衰变是指原子核不稳定,自发地放出粒子或电磁辐射而转变为其他核的过程。
常见的放射性衰变类型有α衰变、β衰变和γ衰变。
三、实验仪器与材料1. 放射性源:含有放射性核素的样品。
2. 计数器:用于测量放射性衰变事件。
3. 秒表:用于计时。
4. 数据记录表格。
5. 计算器。
四、实验步骤1. 准备工作:检查实验仪器是否完好,了解实验原理和步骤。
2. 测量放射性衰变事件:a. 将放射性源放入计数器中,记录计数器开始计时的时刻。
b. 在规定的时间内(如1小时),记录计数器显示的放射性衰变事件数。
c. 记录放射性源的质量、放射性核素的种类和放射性衰变类型。
3. 数据分析:a. 计算放射性衰变事件数与时间的关系,绘制衰变曲线。
b. 根据衰变曲线,计算放射性衰变的半衰期。
c. 分析实验结果,讨论放射性衰变的规律和基本性质。
五、实验结果与分析1. 放射性衰变事件数与时间的关系:根据实验数据,绘制衰变曲线,可以看出放射性衰变事件数随时间呈指数衰减。
2. 放射性衰变的半衰期:根据衰变曲线,计算放射性衰变的半衰期,结果与理论值相符。
3. 放射性衰变的规律:实验结果表明,放射性衰变遵循指数衰减规律,即放射性衰变事件数与时间呈负指数关系。
六、实验讨论1. 放射性衰变的机理:放射性衰变是由于原子核内部的不稳定性导致的,原子核通过放出粒子或电磁辐射来达到稳定状态。
2. 放射性衰变的类型:实验中观察到的放射性衰变类型有α衰变和β衰变,其中α衰变放出α粒子,β衰变放出β粒子。
3. 放射性衰变的半衰期:放射性衰变的半衰期是放射性核素特有的物理常数,反映了放射性核素衰变的快慢。
实验四 核衰变的统计规律与放射性测定的实验数据处理
学生: 学号:同组:
一、实验目的
1. 验证核衰变所服从的统计规律
2. 熟悉放射性测量误差的表示方法
3. 了解测量时间对准确度的影响
4. 学会根据准确度的要求选择测量时间 二 、实验原理
实验证明,在对长寿命放射性物质活度进行多次重复测量时,即使周围条件相同,每次测量的结果仍不相同。
然而,每次结果都围绕某一平均值上下涨落,并且,这种涨落是服从一定的统计规律的。
假如在时间间隔t 内核衰变的平均数为n ,则在某一特定的时间间隔t 内,核衰变为n 的出现机率P(n)服从统计规律的泊松分布:
()()!
n n
n P n e n -= (2-4-1) 图一表示n =的泊松分布曲线。
泊松分布在平均数n 较小的情况下比较适用;如果值相当大,计算起来十分复杂,实际应用对泊松分布利用斯蒂令近似公式: !2n n n n n e π-≈⋅⋅ (2-4-2) 化为高斯分布,得:
2()2()2n n n
P n e
n
π--= (2-4-3)
高斯分布说明,与平均值的偏差()n n -对于n 而言具有对称性,而绝对值大的偏差出现的几率小。
放射性衰变并不是均匀地进行,所以在相同的时间间隔内作重复的测量时测量的放射性粒子数并不严格保持一致,而是在某平均值附近起伏。
通常把平均值n 看作是测量结果的几率值,并用它来表示放射性活度,而把起伏带来的误差叫做测量的统计误差,习惯用标准误差n ±来表描述。
实验室都将一次测量的结果当作平均值,并作类似的处理而计为N N ±。
图 1泊松分布曲线
图 2 高斯分布曲线
计数的相对标准误差为:
= (2-4-4)
它能说明测量的准确度。
当N 大时,相对标准误差小,而准确度高。
反之,则相对标准误差大,而准确度低。
为了得到足够计数N 来保证准确度,就需要延长测量时间t 或增加相同测量的次数m 。
根据计算可知,从时间t 内测的结果中算出的计数率的标准误差为:
t ±
== (2-4-5) 计数率的相对标准误差E 用下式表示:
E == (2-4-6)
若实验重复进行m 次,则平均计数率的标准误差等于:
(2-4-7) 考虑本底后,标准误差为:
σ== (2-4-8) N c 为t c 时间内源加本底的计数,n b 为t b 时间内本底的计数,n c 为源加本底的计数率,n b 为本底的计数率。
放射性测量的相对标准误差:
12()c b c b
c b
n n t t E n n +=±- (2-4-9)
过长测量时间并不有利,因此可合理地分配测定源加本底和本底计数的时间,可利用下列关系式:
c b t t = (2-4-10)
究竟需要选择多长的测量时间,要根据对测量准确度的要求而定,即:
c a t =
(2-4-11) 式中a c b n n n =-为放射源的计数率
当本底与放射率的计数率之比小于给定的准确度(b
a
n E n <)的情况下,上式可近似写为:
2
1
a t n E (2-4-12) 三、实验仪器
计数管、定标器、放射源、铅室和有机玻璃架 四、实验步骤
1. 测量时间对计数率标准误差的影响
(1)接好线路(定标器计数管及电源的电路),打开定标器的检验开关,检查是
否正常;
(2)将高压调到计数管的工作电压在1310V 处,然后侧本底5min ;
(3)将放射源放在计数管下面的适当位置上,然后分别以1min ,5min ,10min
的时间测量源的放射性;
(4)将实验结果填入表内,算出每次测量的标准误差,从中得出必要的结论。
2. 重复测量次数对计数率标准误差的影响
(1)将放射源放在计数管下面的适当位置上,保持几何条件不变,重复测量5
次放射性活度,每次100s ;
(2)将数据列入适当的表格,算出每次测得的计数率的标准误差及5次平均值
的标准误差,从中得出必要的结论,并解释为何5次结果多不相同。
3. 根据放射源活度和测量准确度的要求选择测量时间(相对标准误差为2% ) (1)根据放射源和计数管间的距离,使其计数率为4000脉冲/分~5000脉冲/分。
根据本底与计数率之比相对标准误差之关系,确定选用公式算出测量时间,然后以此时间测量其放射性活度
(2)根据实验数据算出相对标准误差,并与所要求值(2%)相比较。
4. 验证核衰变所服从的统计规律
(1)用放射源计数验证高斯分布,时间间隔以2s 计,使其计数在每2s20次左
右,测量次数最少在800次以上; (2)根据实验数据,绘出高斯分布曲线;
(3)用时间所得平均值根据公式作出高斯分布的理论曲线,比较实验曲线与理
论曲线的不同,并讨论原因。
五 时间数据处理
1. 测量时间对计数率标准误差的影响 本底计数率n b =N b /t b =74/300=脉冲/秒
由表格中的数据可以看出:脉冲计数的标准误差随着时间的不断增加而相对减小,因此,要想在测量时得到比较小的标准误差,有必要延长每次的测量时间。
2. 重复测量次数对计数率标准误差的影响
5次的测量结果之间稍有偏差,是因为核衰变过程是一种随机过程,并不是均匀地进行的,每一个核的衰变是完全独立的,每次测量之间毫无相互依赖关系,所以在相同的时间间隔内作重复的测量时测量的放射性粒子数并不严格保持一致,而是在某平均值附近起伏。
因此,我们应该增加测量次数或采用较长时间测算平均每分的脉冲。
3. 根据放射源的活度选择测量时间(要求E=2% )
n a取平均值为脉冲/秒,n b/n a=<2%,可见本底计数相对于放射源的计数率可以忽略,代入公式2-4-12中,得t≈,近似于40s 。
测量时间t=40s,测量得N c=2754脉冲,因而n c=脉冲/秒;n a=n c-n b=;将数据代入公式2-4-6中,得到E=%(<2%),在给定的范围之内。
4. 验证核衰变所服从的统计规律
高斯计数(t=2s,共测895次,平均计数为52脉冲/秒)
计数n 次数
a
实际几率
P’
理论几
率P
计数
n
次数
a
实际几率
P’
理论几率
P
67110530 73310628 74110725 75110837 76210923 77011020 78411127 79311228 80111327 81211420 82511513 83411617 84411719 8591186 8651194 87111208
计数 n 次数a 实际几率 P’ 理论几
率P 计数 n 次数a 实际几率
P’ 理论几率
P 88 15 121 11 89 11 122 9 90 18 123 5 91 20 124 12 92 14 125 9 93 18 126 9 94 23 127 3 95 22 128 1 96 26 129 2 97 29 130 2 98 24 131 2 99 38 132 1 100 30 133 2 101 44 134 0 102 28 135 2 103 36 139 1 104 38 142 1
193
1
根据有关数据,做出高斯分布的实验曲线,然后用实验所得平均值根据公式(2-4-3)做出理论曲线:
由高斯分布的试验曲线与理论曲线可以看出:实验曲线的整体趋势与理论曲线基本一致,都呈正态分布,只是在实验曲线上相邻的两个计数出现的几率波动较大。
这主要是因为放射性活度数值太高,应该选取更低一点的活度,2s20
P (n )
n
次左右比较合适。
另外核衰变过程是一种随机过程,并不是均匀地进行的,每一个核的衰变是完全独立的,每次测量之间毫无相互依赖关系,也是造成一定波动的原因。
六问题讨论
1.试说明为什么测量时间增长时标准误差会减小
答:由实验原理中的公式(2-4-9)可知,本底计数率越大,对放射性测量的准确度的影响也越大,测量的时间t c和t b越大,准确度就越高。
而且,由时间t 内
测的结果中算出的计数率的标准误差为==因此,在实际测量
过程中,增长测量时间则结果的标准误差就相对减小。
但是,测量时间过长也并非完全有利的,比如外界因素产生影响的几率就增大,另外重复测量也比较困难,因此,应选择合适的测量时间。
2.泊松分布和高斯分布说明了核衰变的什么问题
泊松分布主要适用在平均计数较小的情况下,如果平均值相当大时,计算起来就变得十分麻烦,实际应用中很不方便,这时就可以对其利用斯蒂令近似,化为高斯分布。
很显然,泊松分布和高斯分布均说明:放射性物质的衰变并不是均匀地进行的,在相同的时间间隔内重复测量所测得的放射性计数并不是严格的保持一致,而是在某个平均值上下波动,其整体波动趋势符合正态分布,也即核衰变是符合一定的统计规律的。
并且,在高斯分布曲线中可以看出,与平均值的偏差对于平均值而言具对称性,而其绝对值大小成反比。