第四章模拟调制系统
- 格式:pptx
- 大小:772.99 KB
- 文档页数:103
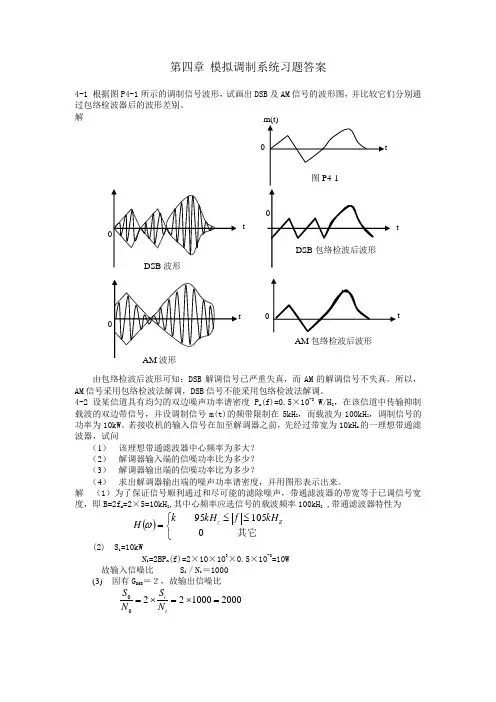
第四章 模拟调制系统习题答案4-1 根据图P4-1所示的调制信号波形,试画出DSB 及AM 信号的波形图,并比较它们分别通解由包络检波后波形可知:DSB 解调信号已严重失真,而AM 的解调信号不失真。
所以,AM 信号采用包络检波法解调,DSB 信号不能采用包络检波法解调。
4-2 设某信道具有均匀的双边噪声功率谱密度P n (f)=0.5×10-3W/H Z ,在该信道中传输抑制载波的双边带信号,并设调制信号m(t)的频带限制在5kH Z ,而载波为100kH Z ,调制信号的功率为10kW 。
若接收机的输入信号在加至解调器之前,先经过带宽为10kH z 的一理想带通滤波器,试问(1) 该理想带通滤波器中心频率为多大? (2) 解调器输入端的信噪功率比为多少? (3) 解调器输出端的信噪功率比为多少?(4) 求出解调器输出端的噪声功率谱密度,并用图形表示出来。
解 (1)为了保证信号顺利通过和尽可能的滤除噪声,带通滤波器的带宽等于已调信号宽度,即B=2f m =2×5=10kH Z ,其中心频率应选信号的载波频率100kH Z ,带通滤波器特性为 ()⎩⎨⎧≤≤=其它010595Zz kH f kH k H ω(2) S i =10kWN i =2BP n (f)=2×10×103×0.5×10-3=10W故输入信噪比 S i /N i =1000 (3) 因有G DSB =2,故输出信噪比 002210002000i iS SN N =⨯=⨯=(4) 根据双边带解调器的输出噪声与输入噪声功率之间的关系,有W N N i 5.2410410===故()()Zn Zm n kH f f p H W f N f P 521105.021/1025.010525.2233300≤=⨯⨯=⨯=⨯⨯==--双其双边谱如右图所示4-3某线性调制系统的输出信噪比为20dB ,输出噪声功率为10-9W ,由发射机输出端到解调器输入端之间总的传输损耗为100dB ,试求:⑴DSB/SC 时的发射机输出功率; ⑵SSB/SC 时的发射机输出功率。





第四章模拟调制4.1学习指导4.1.1要点模拟调制的要点主要包括幅度调制、频率调制和相位调制的工作原理。
1.幅度调制幅度调制是用调制信号去控制载波信号的幅度,使之随调制信号作线性变化的过程。
在时域上,已调信号的振幅随基带信号的规律成正比变化;在频谱结构上,它的频谱是基带信号频谱在频域内的简单平移。
由于这种平移是线性的,因此,振幅调制通常又被称为线性调制。
但是,这里的“线性”并不是已调信号与调制信号之间符合线性变换关系。
事实上,任何调制过程都是一种非线性的变换过程。
幅度调制包括标准调幅(简称调幅)、双边带调幅、单边带调幅和残留边带调幅。
如果调制信号m(t)的直流分量为0,则将其与一个直流量A0相叠加后,再与载波信号相乘,就得到了调幅信号,其时域表达式为stAmttAtmttAM()0()cosc0cosc()cosc(4-1)如果调制信号m(t)的频谱为M(ω),则调幅信号的频谱为1S()πA()()M()M()(4-2)AM0cccc2调幅信号的频谱包括载波份量和上下两个边带。
上边带的频谱结构与原调制信号的频谱结构相同,下边带是上边带的镜像。
由波形可以看出,当满足条件|m(t)|A0(4-3)时,其包络与调制信号波形相同,因此可以用包络检波法很容易恢复出原始调制信号。
否则,出现“过调幅”现象。
这时用包络检波将发生失真,可以采用其他的解调方法,如同步检波。
调幅信号的一个重要参数是调幅度m,其定义为m A m(t)Am(t)0max0minAm(t)Am(t)0max0min(4-4)AM信号带宽B AM是基带信号最高频率分量f H的两倍。
AM信号可以采用相干解调方法实现解调。
当调幅度不大于1时,也可以采用非相干解调方法,即包络检波,实现解调。
双边带信号的时域表达式为stmttDSB()()cosc(4-5)其中,调制信号m(t)中没有直流分量。
如果调制信号m(t)的频谱为M(ω),双边带信号的频谱为1S()M()M()(4-6)DSBcc2与AM信号相比,双边带信号中不含载波分量,全部功率都用于传输用用信号,调制效率达到100%。



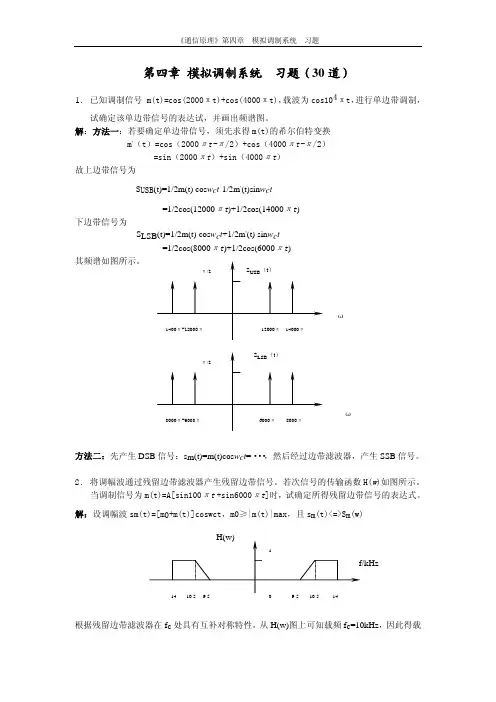
第四章 模拟调制系统 习题(30道)1. 已知调制信号 m(t)=cos(2000πt)+cos(4000πt),载波为cos104πt,进行单边带调制,试确定该单边带信号的表达试,并画出频谱图。
解:方法一:若要确定单边带信号,须先求得m(t)的希尔伯特变换 m ’(t)=cos(2000πt-π/2)+cos(4000πt-π/2) =sin(2000πt )+sin(4000πt ) 故上边带信号为S USB (t)=1/2m(t) cos w c t -1/2m ’(t)sin w c t =1/2cos(12000πt )+1/2cos(14000πt ) 下边带信号为S LSB (t)=1/2m(t) cos w c t +1/2m ’(t) sin w c t=1/2cos(8000πt )+1/2cos(6000πt ) 其频谱如图所示。
方法二:先产生DSB 信号:s m (t)=m(t)cos w c t =···,然后经过边带滤波器,产生SSB 信号。
2. 将调幅波通过残留边带滤波器产生残留边带信号。
若次信号的传输函数H(w )如图所示。
当调制信号为m(t)=A[sin100πt +sin6000πt ]时,试确定所得残留边带信号的表达式。
解:设调幅波sm(t)=[m 0+m(t)]coswct,m0≥|m(t)|max,且s m (t)<=>S m (w)根据残留边带滤波器在f c 处具有互补对称特性,从H(w)图上可知载频f c =10kHz ,因此得载波cos20000πt。
故有sm(t)=[m0+m(t)]cos20000πt=m0cos20000πt+A[sin100πt+sin6000πt]cos20000πt=m0cos20000πt+A/2[sin(20100πt)-sin(19900πt)+sin(26000πt)-sin(14000πt)Sm(w)=πm0[σ(w+20000π)+σ(W-20000π)]+jπA/2[σ(w+20100π)-σ(w+19900π)+σ(w-19900π)+σ(w+26000π)-σ(w-26000π)-σ(w+14000π)+σ(w-14000π)残留边带信号为F(t),且f(t)<=>F(w),则F(w)=Sm(w)H(w)故有:F(w)=π/2m0[σ(w+20000π)+σ(w-20000π)]+jπA/2[0.55σ(w+20100π)-0.55σ(w-20100π)-0.45σ(w+19900π)+ 0.45σ(w-19900π)+σ(w+26000π) -σ(w-26000π)f(t)=1/2m0cos20000πt+A/2[0.55sin20100πt-0.45sin19900πt+sin26000πt]3.设某信道具有均匀的双边噪声功率谱密度Pn(f)=0.5*10-3W/Hz,在该信道中传输抑制载波的双边带信号,并设调制信号m(t)的频带限制在5kHz,而载波为100kHz,已调信号的功率为10kW.若接收机的输入信号在加至解调器之前,先经过一理想带通滤波器滤波,试问:1.)该理想带通滤波器应具有怎样的传输特性H(w)?2.)解调器输入端的信噪功率比为多少?3.)解调器输出端的信噪功率比为多少?4.)求出解调器输出端的噪声功率谱密度,并用图型表示出来。
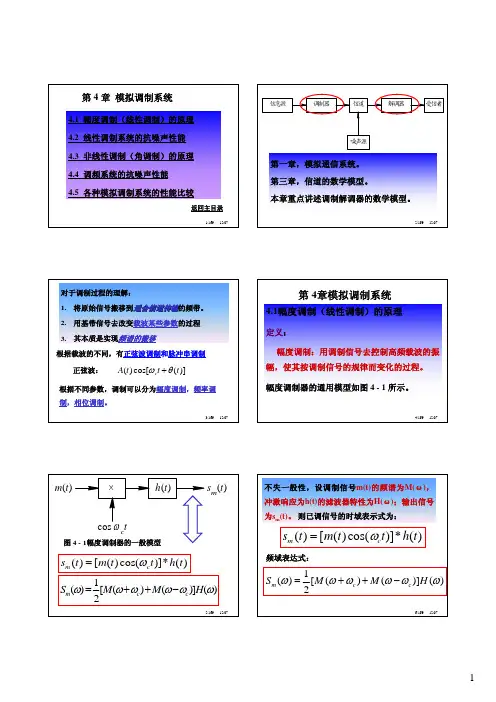
第四章 模拟调制系统习题答案4-1 根据图P4-1所示的调制信号波形,试画出DSB 及AM 信号的波形图,并比较它们分别解由包络检波后波形可知:DSB 解调信号已严重失真,而AM 的解调信号不失真。
所以,AM 信号采用包络检波法解调,DSB 信号不能采用包络检波法解调。
4-2 设某信道具有均匀的双边噪声功率谱密度P n (f)=0.5×10-3 W/H Z ,在该信道中传输抑制载波的双边带信号,并设调制信号m(t)的频带限制在5kH Z ,而载波为100kH Z ,调制信号的功率为10kW 。
若接收机的输入信号在加至解调器之前,先经过带宽为10kH z 的一理想带通滤波器,试问(1) 该理想带通滤波器中心频率为多大? (2) 解调器输入端的信噪功率比为多少? (3) 解调器输出端的信噪功率比为多少?(4) 求出解调器输出端的噪声功率谱密度,并用图形表示出来。
解 (1)为了保证信号顺利通过和尽可能的滤除噪声,带通滤波器的带宽等于已调信号宽度,即B=2f m =2×5=10kH Z ,其中心频率应选信号的载波频率100kH Z ,带通滤波器特性为 ()⎩⎨⎧≤≤=其它010595Zz kH f kH k H ω(2) S i =10kWN i =2BP n (f)=2×10×103×0.5×10-3=10W故输入信噪比 S i /N i =1000 (3) 因有G DSB =2,故输出信噪比 002210002000i iS SN N =⨯=⨯=(4) 根据双边带解调器的输出噪声与输入噪声功率之间的关系,有W N N i 5.2410410===故()()Zn Zm n kH f f p H W f N f P 521105.021/1025.010525.2233300≤=⨯⨯=⨯=⨯⨯==--双其双边谱如右图所示4-3某线性调制系统的输出信噪比为20dB ,输出噪声功率为10-9W ,由发射机输出端到解调器输入端之间总的传输损耗为100dB ,试求:⑴DSB/SC 时的发射机输出功率; ⑵SSB/SC 时的发射机输出功率。