知识讲解独立重复试验与二项分布
- 格式:doc
- 大小:86.50 KB
- 文档页数:10


第8讲n次独立重复试验与二项分布基础知识整合1.条件概率及其性质2.事件的相互独立(1)设A,B为两个事件,如果P(AB)=□05P(A)·P(B),那么称事件A与事件B相互独立.(2)如果事件A与B相互独立,那么□06A与□07B,□08A与□09B,□10 A与□11B也都相互独立.3.独立重复试验与二项分布(1)独立重复试验在相同条件下重复做的n次试验称为n次独立重复试验,即若用A i(i=1,2,…,n)表示第i次试验结果,则P(A1A2A3…A n)=□12P(A1)P(A2)P(A3)…P(A n).(2)二项分布在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为P(X=k)=□13C k n p k(1-p)n-k(k=0,1,2,…,n),此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率.1.A ,B 中至少有一个发生的事件为A ∪B . 2.A ,B 都发生的事件为AB . 3.A ,B 都不发生的事件为A -B -.4.A ,B 恰有一个发生的事件为(A B -)∪(A -B ).5.A ,B 至多一个发生的事件为(A B )∪(A B )∪(A B ).1.甲射击命中目标的概率为0.75,乙射击命中目标的概率为23,当两人同时射击同一目标时,该目标被击中的概率为( )A.12 B .1 C.1112 D.56 答案 C解析 1-13×14=1112,选C.2.由0,1组成的三位编号中,若用A 表示“第二位数字为0的事件”,用B 表示“第一位数字为0的事件”,则P (A |B )=( )A.12B.14C.16D.18 答案 A解析 因为第一位数字可为0或1,所以第一位数字为0的概率P (B )=12,第一位数字为0且第二位数字也是0,即事件A ,B 同时发生的概率P (AB )=12×12=14,所以P (A |B )=P (AB )P (B )=1412=12.3.(2019·吉林通化模拟)若ξ~B ⎝ ⎛⎭⎪⎫10,12,则P (ξ≥2)等于( )A.10131024B.111024C.501512D.507512 答案 A 解析P (ξ≥2)=1-P (ξ=0)-P (ξ=1)=1-C 010⎝ ⎛⎭⎪⎫1210-C 110⎝ ⎛⎭⎪⎫1210=10131024.4.(2019·广东汕头模拟)甲、乙两人参加“社会主义价值观”知识竞赛,甲、乙两人能荣获一等奖的概率分别为23和34,甲、乙两人是否获得一等奖相互独立,则这两个人中恰有一人获得一等奖的概率为( )A.34B.23C.57D.512 答案 D解析 根据题意,恰有一人获得一等奖就是甲获奖乙没获奖或甲没获奖乙获奖,则所求概率是23×⎝ ⎛⎭⎪⎫1-34+34×⎝ ⎛⎭⎪⎫1-23=512.故选D.5.(2019·福建厦门模拟)袋中装有2个红球,3个黄球,有放回地抽取3次,每次抽取1球,则3次中恰有2次抽到黄球的概率是( )A.25B.35C.18125D.54125 答案 D解析 袋中装有2个红球,3个黄球,有放回地抽取3次,每次抽取1球,每次取到黄球的概率P 1=35,∴3次中恰有2次抽到黄球的概率是P =C 23⎝ ⎛⎭⎪⎫352⎝ ⎛⎭⎪⎫1-35=54125.6.袋中有红、黄、蓝球各1个,从中有放回地每次任取1个,直到取到红球为止,则第4次首次取到红球的概率为( )A.980B.881C.382D.827 答案 B解析 前3次都取不到红球的概率为⎝ ⎛⎭⎪⎫233,第4次首次取到红球的概率为13,4个独立事件同时发生的概率为⎝ ⎛⎭⎪⎫233×13=881.核心考向突破考向一 条件概率例1 (1)(2019·大庆模拟)从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到的2个数均为偶数”,则P (B |A )=( )A.18B.14C.25D.12答案 B解析P(A)=C23+C22C25=25,P(B)=C22C25=110,又A⊇B,则P(AB)=P(B)=110,所以P(B|A)=P(AB)P(A)=P(B)P(A)=14.(2)(2019·江西南昌模拟)口袋中装有大小、形状相同的红球2个,白球3个,黄球1个,甲从中不放回地逐一取球,已知第一次取得红球,则第二次取得白球的概率为________.答案3 5解析口袋中装有大小形状相同的红球2个,白球3个,黄球1个,甲从中不放回地逐一取球,设事件A表示“第一次取得红球”,事件B表示“第二次取得白球”,则P(A)=26=13,P(AB)=26×35=15,∴第一次取得红球后,第二次取得白球的概率为P(B|A)=P(AB)P(A)=1513=35.触类旁通条件概率的求法(1)定义法:先求P(A)和P(AB),再由P(B|A)=P(AB)P(A)求P(B|A).即时训练 1.某个电路开关闭合后会出现红灯或绿灯闪烁,已知开关第一次闭合后出现红灯的概率为12,两次闭合后都出现红灯的概率为15,则在第一次闭合后出现红灯的条件下第二次闭合后出现红灯的概率为()A.110 B.15 C.25 D.12答案 C解析设“开关第一次闭合后出现红灯”为事件A,“第二次闭合后出现红灯”为事件B ,则由题意可得P (A )=12,P (AB )=15,则在第一次闭合后出现红灯的条件下第二次闭合出现红灯的概率是P (B |A )=P (AB )P (A )=1512=25.故选C.2.有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8,在这批种子中,随机抽取一粒,则这粒种子能成长为幼苗的概率为________.答案 0.72解析 设种子发芽为事件A ,种子成长为幼苗为事件AB (发芽,又成活为幼苗),出芽后的幼苗成活率为P (B |A )=0.8,P (A )=0.9, 由P (B |A )=P (AB )P (A ),得P (AB )=P (B |A )·P (A )=0.9×0.8=0.72. 故这粒种子成长为幼苗的概率为0.72. 考向二 相互独立事件的概率例2 (2017·天津高考)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为12,13,14.(1)记X 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X 的分布列和数学期望;(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率. 解 (1)随机变量X 的所有可能取值为0,1,2,3. P (X =0)=⎝ ⎛⎭⎪⎫1-12×⎝ ⎛⎭⎪⎫1-13×⎝ ⎛⎭⎪⎫1-14=14,P (X =1)=12×⎝ ⎛⎭⎪⎫1-13×⎝ ⎛⎭⎪⎫1-14+⎝ ⎛⎭⎪⎫1-12×13×⎝ ⎛⎭⎪⎫1-14+⎝ ⎛⎭⎪⎫1-12×⎝ ⎛⎭⎪⎫1-13×14=1124,P (X =2)=⎝ ⎛⎭⎪⎫1-12×13×14+12×⎝ ⎛⎭⎪⎫1-13×14+12×13×⎝ ⎛⎭⎪⎫1-14=14,P (X =3)=12×13×14=124.所以随机变量X 的分布列为随机变量X的数学期望E(X)=0×14+1×1124+2×14+3×124=1312.(2)设Y表示第一辆车遇到红灯的个数,Z表示第二辆车遇到红灯的个数,则所求事件的概率为P(Y+Z=1)=P(Y=0,Z=1)+P(Y=1,Z=0)=P(Y=0)P(Z=1)+P(Y=1)P(Z=0)=14×1124+1124×14=1148.所以这2辆车共遇到1个红灯的概率为11 48.触类旁通求相互独立事件同时发生的概率的方法(1)相互独立事件同时发生的概率等于他们各自发生的概率之积;(2)当正面计算较复杂或难以入手时,可从其对立事件入手计算.即时训练 3.某乒乓球俱乐部派甲、乙、丙三名运动员参加某运动会的单打资格选拔赛,本次选拔赛只有出线和未出线两种情况.规定一名运动员出线记1分,未出线记0分.假设甲、乙、丙出线的概率分别为23,34,35,他们出线与未出线是相互独立的.(1)求在这次选拔赛中,这三名运动员至少有一名出线的概率;(2)记在这次选拔赛中,甲、乙、丙三名运动员的得分之和为随机变量ξ,求随机变量ξ的分布列和数学期望E(ξ).解(1)记“甲出线”为事件A,“乙出线”为事件B,“丙出线”为事件C,“甲、乙、丙至少有一名出线”为事件D,则P(D)=1-P(A-B-C-)=1-13×14×25=2930.(2)由题意可得,ξ的所有可能取值为0,1,2,3,则P(ξ=0)=P(A-B-C-)=13×14×25=130;P(ξ=1)=P(A B-C-)+P(A-B C-)+P(A-B-C)=23×14×25+13×34×25+13×14×35=13 60;P(ξ=2)=P(AB C-)+P(A B-C)+P(A-BC)=23×34×25+23×14×35+13×34×35=920;P(ξ=3)=P(ABC)=23×34×35=310.所以ξ的分布列为E(ξ)=0×130+1×1360+2×920+3×310=12160.考向三独立重复实验与二项分布例3(2019·重庆模拟)为了应对新疆暴力恐怖活动,重庆市警方从武警训练基地挑选反恐警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选.假定某基地有4名武警战士(分别记为A,B,C,D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为23,23,12.这三项测试能否通过相互之间没有影响.(1)求A能够入选的概率;(2)规定:按入选人数得训练经费,每入选1人,则相应的训练基地得到5000元的训练经费,求该基地得到训练经费的分布列与数学期望(期望精确到个位).解(1)设A通过体能、射击、反应分别记为事件M,N,P,则A能够入选包含以下几个互斥事件:MN P-,M N-P,M-NP,MNP,∴P(A)=P(MN P-)+P(M N-P)+P(M-NP)+P(MNP)=23×23×12+23×13×12+13×23×12+23×23×12=1218=23.(2)记ξ表示该训练基地入选人数,则得到的训练经费为η=5000ξ,又ξ的可能取值为0,1,2,3,4,∴P (ξ=0)=C 04⎝ ⎛⎭⎪⎫230⎝ ⎛⎭⎪⎫134=181, P (ξ=1)=C 14⎝ ⎛⎭⎪⎫231⎝ ⎛⎭⎪⎫133=881, P (ξ=2)=C 24⎝ ⎛⎭⎪⎫232⎝ ⎛⎭⎪⎫132=2481=827, P (ξ=3)=C 34⎝ ⎛⎭⎪⎫233⎝ ⎛⎭⎪⎫131=3281,P (ξ=4)=C 44⎝ ⎛⎭⎪⎫234⎝ ⎛⎭⎪⎫130=1681. ∴ξ的分布列为触类旁通求解独立重复试验概率时应注意的问题(1)概率模型是否满足公式P n (k )=C k n p k (1-p )n -k的三个条件:①在一次试验中某事件A 发生的概率是一个常数p ;②n 次试验不仅是在完全相同的情况下进行的重复试验,而且各次试验的结果是相互独立的;③该公式表示n 次试验中事件A 恰好发生了k 次的概率.(2)独立重复试验是相互独立事件的特例(概率公式也是如此),就像对立事件是互斥事件的特例一样,只要有“恰好”字样的题用独立重复试验的概率公式计算更简单,就像有“至少”或“至多”等字样的题用对立事件的概率公式计算更简单一样.即时训练 4.某学校为了丰富学生的课余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取一首,背诵正确加10分,背诵错误减10分,且背诵结果只有“正确”和“错误”两种.其中某班级学生背诵正确的概率p =23,记该班级完成n 首背诵后的总得分为S n .(1)求S 6=20且S i ≥0(i =1,2,3)的概率; (2)记ξ=|S 5|,求ξ的分布列及数学期望.解 (1)当S 6=20时,即背诵6首后,正确的有4首,错误的有2首. 由S i ≥0(i =1,2,3)可知,若第一首和第二首背诵正确,则其余4首可任意背诵正确2首;若第一首背诵正确,第二首背诵错误,第三首背诵正确,则其余3首可任意背诵正确2首.则所求的概率P =⎝ ⎛⎭⎪⎫232×C 24⎝ ⎛⎭⎪⎫232×⎝ ⎛⎭⎪⎫132+23×13×23×C 23⎝ ⎛⎭⎪⎫232×13=1681. (2)由题意知ξ=|S 5|的所有可能的取值为10,30,50,又p =23, ∴P (ξ=10)=C 35⎝ ⎛⎭⎪⎫233×⎝ ⎛⎭⎪⎫132+C 25⎝ ⎛⎭⎪⎫232×⎝ ⎛⎭⎪⎫133=4081, P (ξ=30)=C 45⎝ ⎛⎭⎪⎫234×⎝ ⎛⎭⎪⎫131+C 15⎝ ⎛⎭⎪⎫231×⎝ ⎛⎭⎪⎫134=3081, P (ξ=50)=C 55⎝ ⎛⎭⎪⎫235×⎝ ⎛⎭⎪⎫130+C 05⎝ ⎛⎭⎪⎫230×⎝ ⎛⎭⎪⎫135=1181, ∴ξ的分布列为∴E (ξ)=10×4081+30×3081+50×1181=185081.。
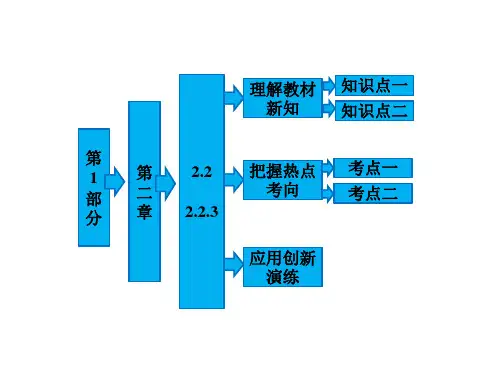








独立重复试验与二项分布【学习目标】1.理解n次独立重复试验模型及二项分布.2.能利用n次独立重复试验及二项分布解决一些简单的实际问题.【要点梳理】要点一、n次独立重复试验每次试验只考虑两种可能结果与,并且事件发生的概率相同。
在相同的条件下重复地做次试验,各次试验的结果相互独立,称为次独立重复试验。
要点诠释:在次独立重复试验中,一定要抓住四点:①每次试验在同样的条件下进行;②每次试验只有两种结果与,即某事件要么发生,要么不发生;③每次试验中,某事件发生的概率是相同的;④各次试验之间相互独立。
总之,独立重复试验,是在同样的条件下重复的,各次之间相互独立地进行的一种试验,在这种试验中,每一次的试验结果只有两种,即某事件要么发生,要么不发生,并且任何一次试验中发生的概率都是一样的。
要点二、独立重复试验的概率公式1.定义如果事件A在一次试验中发生的概率为P,那么n次独立重复试验中,事件A恰好发生k次的概率为:(k=0,1,2,…,n).令得,在n次独立重复试验中,事件A没有发生的概率为........令得,在n次独立重复试验中,事件A全部发生的概率为........。
要点诠释:1. 在公式中,n是独立重复试验的次数,p是一次试验中某事件A发生的概率,k是在n次独立重复试验中事件A恰好发生的次数,只有弄清公式中n,p,k的意义,才能正确地运用公式.2. 独立重复试验是相互独立事件的特例,就像对立事件是互斥事件的特例一样,只是有“恰好”字样的用独立重复试验的概率公式计算更方便.要点三、n次独立重复试验常见实例:1.反复抛掷一枚均匀硬币2.已知产品率的抽样3.有放回的抽样4.射手射击目标命中率已知的若干次射击要点诠释:抽样问题中的独立重复试验模型:①从产品中有放回地抽样是独立事件,可按独立重复试验来处理; ②从小数量的产品中无放回地抽样不是独立事件,只能用等可能事件计算;③从大批量的产品中无放回地抽样,每次得到某种事件的概率是不一样的,但由于差别太小,相当于是独立事件,所以一般情况下仍按独立重复试验来处理。
要点四、离散型随机变量的二项分布 1. 定义:在一次随机试验中,事件A 可能发生也可能不发生,在次独立重复试验中事件A 发生的次数是一个离散型随机变量.如果在一次试验中事件A 发生的概率是,则此事件不发生的概率为,那么在次独立重复试验中事件A 恰好发生次的概率是,().于是得到离散型随机变量的概率分布如下:由于表中第二行恰好是二项展开式中各对应项的值,所以称这样的随机变量服从参数为,的二项分布,记作. 要点诠释:判断一个随机变量是否服从二项分布,关键有三: 其一是独立性。
即每次试验的结果是相互独立的; 其二是重复性。
即试验独立重复地进行了n 次;其三是试验的结果的独特性。
即一次试验中,事件发生与不发生,二者必居其一。
2.如何求有关的二项分布(1)分清楚在n 次独立重复试验中,共进行了多少次重复试验,即先确定n 的值,然后确定在一次试验中某事件A 发生的概率是多少,即确定p 的值,最后再确定某事件A 恰好发生了多少次,即确定k 的值;(2)准确算出每一种情况下,某事件A 发生的概率; (3)用表格形式列出随机变量的分布列。
【典型例题】类型一、独立重复试验的概率例 1.某气象站天气预报的准确率为80%,计算(结果保留到小数点后第2位): (1)5次预报中恰有2次准确的概率; (2)5次预报中至少有2次准确的概率;(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.【思路点拨】5次预报相当于做了5次独立重复试验.利用独立重复试验公式即可. 【解析】(1)5次预报中恰有2次准确的概率为 .(2)5次预报中至少有2次准确的概率为 51(0)P P =--.(3)5次预报中恰有2次准确,且其中第3次预报准确的概率为.【总结升华】解决此类问题,首先应明确是否是n次独立重复试验,其次要弄清公式中n和k的值以及p的值.举一反三:【变式1】甲每次投资获利的概率是p=,对他进行的6次相互独立的投资,计算:(1)有5次获利的概率;(2)6次都获利的概率;(3)至少5次获利的概率.【答案】用X表示甲在6次投资中获利的次数,则X服从二项分布B(6,),且,.(1)他5次获利的概率约等于.(2)他6次都获利的概率约等于.(3){X≥5}表示他至少5次获利,且{X≥5}={X=5}∪{X=6}.由于事件{X=5}和{X=6}互斥,所以P(X≥5)=P(X=5)+P(X=6)≈+=.故他至少5次获利的概率约等于.【变式2】若,则等于()A. B. C. D.【答案】D;。
【变式3】十层电梯从低层到顶层停不少于3次的概率是多少?停几次概率最大?【解析】依题意,从低层到顶层停不少于3次,应包括停3次,停4次,停5次,……,直到停9次∴从低层到顶层停不少于3次的概率设从低层到顶层停次,则其概率为,∴当或时,最大,即最大,答:从低层到顶层停不少于3次的概率为,停4次或5次概率最大.例2.甲、乙两队进行排球比赛,已知在一局比赛中甲队胜的概率为,没有平局.(1)若进行三局两胜制比赛,先胜两局者为胜,则甲获胜的概率是多少?(2)若进行五局三胜制比赛,则甲获胜的概率是多少?【思路点拨】本题考查概率基础知识、独立重复试验等.(1)中应先分类,甲前两局胜,或一、三局胜,或二、三局胜.(2)中用同样的方法分类.【解析】(1)甲第一、二局胜,或第二、三局胜,或第一、三局胜。
则.(2)甲前三局胜,或甲第四局胜而前三局仅胜两局,或甲第五局胜而前四局仅胜两局,则【总结升华】本题中,无论比赛几局,只要甲获胜,必须甲在最末一局胜,如比赛3局,甲以2:1获胜,须前两局中甲胜一局负一局,第三局甲胜.举一反三:【变式】已知乒乓球选手甲、乙进行比赛,而且他们在每一局中获胜的概率都是,规定使用“七局四胜制”,即先赢四局者胜。
(1)试求甲分别打完四局、五局、六局、七局才获胜的概率;(2)设比赛局数为X,求离散型随机变量X的分布列。
【答案】(1)根据比赛规定使用“七局四胜制”,即先赢四局者胜,则:①记事件A1=“甲连胜四局”,所以甲打完四局就获胜的概率为:;②记事件A2=“在前四局比赛中甲胜三局且第五局也胜”,所以甲打完五局才获胜的概率为:;③记事件A3=“在前五局比赛中甲胜三局且第六局也胜”,所以甲打完六局才获胜的概率为:;④记事件A4=“前六局比赛中甲胜三局且第七局也胜”,所以甲打完七局才获胜的概率为:。
(2)由题意可知,比赛局数X的可能取值为4,5,6,7,并且每种情况比赛总有一人获胜,故离散型随机变量X的分布列为类型二、离散型随机变量的二项分布例3. 一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。
(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分的概率分布列。
【思路点拨】有放回地依次取3次,相当于三次独立重复试验,其得分服从二项分布,故可用n次独立重复试验的概率公式来计算,从而写出分布列。
【解析】(Ⅰ)设“一次取出3个球得4分”的事件记为A,它表示取出的球中有1个红球和2个黑球的情况,则(Ⅱ)由题意,的可能取值为3.4.5.6。
因为是有放回地取球,所以每次取到红球的概率为的分布列为【总结升华】①本题的关键是首先确定进行了三次独立重复试验,然后确定每次试验的结果相互独立,从而可知离散型随机变量服从二项分布,然后运用n 次独立重复试验的概率公式计算。
②注意n 次独立重复试验中,离散型随机变量X 服从二项分布,即,这里n 是独立重复试验的次数,p 是每次试验中某事件发生的概率。
举一反三:【变式1】某厂生产电子元件,其产品的次品率为5%.现从一批产品中任意地连续取出2件,写出其中次品数ξ的概率分布.【答案】依题意,随机变量ξ~B (2,5%).所以,P (ξ=0)=(95%)=,P (ξ=1)=(5%)(95%)=, P ()=(5%)=.因此,次品数ξ的概率分布是【变式2】一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是。
(1)求这名学生在途中遇到红灯的次数ξ的分布列;(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;(3) 这名学生在途中至少遇到一次红灯的概率.解:(1)ξ:B (5, ),ξ的分布列为P (ξ=k )=5512()()33kkkC -,k =0,1,2,3,4,5;(2)η的分布列为P (η=k )=p (前k 个是绿灯,第k +1个是红灯)=21()33k⋅,k =0,1,2,3,4;P (η=5)=P (5个均为绿灯)=52()3;(3)所求概率=P (ξ≥1)=1-P (ξ=0)=1-52211()3243=≈. 【变式3】一袋中有5个白球,3个红球,每次任取一个,取出后记下球的颜色,然后放回,直到红球出现10次时停止,设停止时总共取了X 次球,求X 的分布列及P (X=12).【答案】由题意知,X 是取球次数,X=10,11,12,…,且每次取得红球的概率是,取得白球的概率是,所以X=k (k=10,11,12…)表示取了k 次球,且第k 次取到的是红球,前(k -1)次取得9次红球.∴X 的分布列为91()k P X k C -==(k=10,11,…),(表格略).【变式4】某射手击中目标的概率为,现有4发子弹,击中目标或打完子弹就停止射击,求射击次数X的概率分布.【答案】错解: X的可能取值是1,2,3,4.P(X=1)=;;;.所以X的概率分布列为错解分析:错将本题理解为二项分布,本题实质上不是二项分布,而是求事件A首次发生出现在第k次试验中的概率,要使首次发生出现在第k次试验,必须而且只需在前(k-1)次试验中都出现.正解 X的可能取值是1,2,3,4.P(X=1)=;P(X=2)=×=;P(X=3)=×=;P(X=4)==.所以X的概率分布列为类型三、独立重复试验与二项分布综合应用例4.甲、乙两人各射击一次,击中目标的概率分别是 .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.(1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?【思路点拨】本题的第一问是一个独立事件同时发生的问题,每次射中目标都是相互独立的、可以重复射击即事件重复发生、每次都只有发生或不发生两种情形且发生的概率是相同的.第二问解答时要认清限制条件的意义.【解析】(1)记“甲连续射击4次,至少1次未击中目标”为事件A1,由题意,射击4次,相当于4次独立重复试验,故P(A1)=答:甲射击4次,至少1次未击中目标的概率为;(2) 记“乙恰好射击5次后,被中止射击”为事件A3,“乙第i次射击未击中” 为事件D i,(i=1,2,3,4,5),则,由于各事件相互独立,故答:乙恰好射击5次后,被中止射击的概率是【总结升华】射击问题必须弄清所求目标的含义,是否为独立重复试验,再用排列组合知识求解。