(完整版)八年级下四边形知识点经典题型要点总结
- 格式:docx
- 大小:129.48 KB
- 文档页数:11

初二数学平行四边形7大常见题型+知识点+误区平行四边形是初二数学必考内容,甚至于中考卷里也时常出现它的身影,而且所占分值还不少。
为此,特意给大家整理了初二数学下册必考之【平行四边形】,7大常见题型+知识点+误区!平行四边形定义:有两组对边分别平行的四边形是平行四边形。
表示:平行四边形用符号“□”来表示。
平行四边形性质:平行四边形对边相等;平行四边形对角相等;平行四边形对角线互相平分平行四边形的面积等于底和高的积,即S□ABCD=ah,其中a可以是平行四边形的任何一边,h必须是a边到其对边的距离,即对应的高。
平行四边形的判定:两组对边分别平行的四边形是平行四边形两组对角分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形从对角线看:对角钱互相平分的四边形是平行四边形从角看:两组对角分别相等的四边形是平行四边形。
若一条直线过平行四边形对角线的交点,则直线被一组对边截下的线段以对角线的交点为中点,且这条直线二等分平行四边形的面积。
7大常见题型分析(1)利用平行四边形的性质,求角度、线段长、周长等例题1:如图,E、F在ABCD的对角线AC上,AE=EF=CD,∠ADF=90°,∠BCD=54°,求∠ADE的度数分析:直角三角形斜边上的中线等于斜边的一半,由此可以得到DE=AE=EF=CD,多条线段相等,可设最小的角为x,即设∠EAD=∠ADE=x,根据外角等于不相邻的内角和,得到∠DEC=∠DCE=2x,由平行四边形的性质得出∠DCE=∠BCD-∠BCA=54°-x,得出方程,解方程即可。
例题2:如图,已知四边形ABCD和四边形ADEF均为平行四边形,点B,C,F,E在同一直线上,AF交CD于O,若BC=10,AO=FO,求CE的长。
分析:根据平行四边形的性质得出AD=BC=EF,AD∥BE,从而得到∠DAO=∠CFO,再加上对顶角相等,可以得到△AOD≌△FOC,根据全等三角形的性质得到AD=CF,即AD=BC=EF=CF,从而得到线段CE的长度。

第 9 章四边形〔请记熟前两页〕对边不平行的四边形一般梯形梯形等腰梯形四边形特别梯形直角梯形矩形平行四边形}正方形菱形一、平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
性质: 1、对边:分别平行且相等;2、对角:分别相等;3、对角线:互相均分;4、对称性:中心对称图形。
判判定理 1 、两组对边分别平行的四边形是平行四边形〔定义〕;2、两组对边分别相等的四边形是平行四边形;3、一组对边平行且相等的四边形是平行四边形;4、两组对角分别相等的四边形是平行四边形;5、对角线互相均分的四边形是平行四边形。
三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
二、矩形定义:有一个角是直角的平行四边形。
性质: 1、拥有平行四边形的所有性质;2、四个角都是直角;3、对角线互相均分且相等;4、对称性:中心对称图形,轴对称图形。
判判定理: 1. 有一个角是直角的平行四边形叫做矩形。
2.对角线相等的平行四边形是矩形。
3.有三个角是直角的四边形是矩形。
A直角三角形斜边上的中线等于斜边的一半。
DC B三、菱形定义:邻边相等的平行四边形。
性质: 1、拥有平行四边形的所有性质;2、四条边都相等;3、对角线互相垂直,并且每一条对角线均分一组对角;4、对称性:中心对称图形、轴对称。
判判定理: 1. 一组邻边相等的平行四边形是菱形〔定义〕;2.对角线互相垂直的平行四边形是菱形;3.四条边相等的四边形是菱形。
S 菱形 =1/2 ×ab〔 a、 b 为两条对角线〕四、正方形定义:一个角是直角的菱形或邻边相等的矩形。
性质: 1、四条边都相等;2、四个角都是直角;3、正方形既是矩形,又是菱形。
判判定理: 1、邻边相等的矩形是正方形。
2、有一个角是直角的菱形是正方形。
五、梯形定义:一组对边平行,另一组对边不平行的四边形叫做梯形。
1、直角梯形的定义:有一个角是直角的梯形2、等腰梯形的定义:两腰相等的梯形。

八年级下四边形知识点经典题型要点总结在八年级下册的数学学习中,四边形是一个重要的几何图形,其中包括了矩形、正方形、菱形、平行四边形、梯形等等。
通过对于这些四边形的学习和掌握,不仅可以提高我们的空间想象力,还有助于解决实际问题。
在本文中,我们将总结四边形的知识点和经典题型要点,帮助大家更好地掌握这一部分内容。
1. 矩形矩形是一个具有四个直角的四边形,其特点是对角线相等,对边平行且相等。
矩形的相关要点包括:- 周长计算公式:周长 = 2 × (长 + 宽)- 面积计算公式:面积 = 长 ×宽- 对角线长度相等:对角线长度等于 $\sqrt{长^2 + 宽^2}$2. 正方形正方形是一种特殊的矩形,其特点是四个边和四个角都相等。
正方形的相关要点包括:- 周长计算公式:周长 = 4 ×边长- 面积计算公式:面积 = 边长 ×边长- 对角线长度:对角线长度等于边长 × $\sqrt{2}$3. 菱形菱形是一种具有对边平行且相等的四边形,其特点是所有角都是直角。
菱形的相关要点包括:- 周长计算公式:周长 = 4 ×边长- 面积计算公式:面积 = 对角线之积的一半- 对角线的长度关系:对角线互相垂直且相等4. 平行四边形平行四边形是一种具有对边平行且相等的四边形,其特点是对角线互相平分。
平行四边形的相关要点包括:- 周长计算公式:周长 = 2 × (边长1 + 边长2)- 面积计算公式:面积 = 底边 ×高- 对角线的长度和关系:对角线长度等于 $\sqrt{边长1^2 + 边长2^2 + 2×底边×高^2}$5. 梯形梯形是一种具有两条平行边的四边形,其特点是底边和顶边平行且相等。
梯形的相关要点包括:- 周长计算公式:周长 = 底边1 + 底边2 + 左斜边 + 右斜边- 面积计算公式:面积 = (底边1 + 底边2) ×高 / 2通过对于这些四边形的学习和掌握,我们可以更好地解决与其相关的问题。

第19章四边形知识点
一、平行四边形
1、平行四边形定义:(即是性质又是判定)
2、平行四边形的性质:边:
角:
对角线:
对称性:
面积公式:
3、平行四边形的判定:
4、中位线定理:。
二、矩形
1、矩形的定义:。
矩形判定定理:
推论:
三、菱形
1、菱形的定义 :
2、菱形的性质:
3、菱形的判定:
4、菱形的面积公式:
四、正方形
1、正方形定义: 。
2、正方形的性质:
3、正方形判定定理:
(1)先证四边形是 ,再证 。
(2)先证四边形是 ,再证 。
五、中点四边形
顺次连接任意一个四边形各边的中点所得的四边形是 。
平行四边形的中点四边形是 。
矩形的中点四边形是 。
菱形的中点四边形是 。

初二数学四边形考点归纳初二数学有关四边形的常考知识点都有哪些呢?下面店铺为大家带来初二数学四边形考点归纳,欢迎大家学习!初二数学四边形考点归纳:平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等。
平行四边形的对角线互相平分。
平行四边形的判定 1.两组对边分别相等的四边形是平行四边形2.对角线互相平分的四边形是平行四边形;3.两组对角分别相等的四边形是平行四边形;4.一组对边平行且相等的四边形是平行四边形。
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
直角三角形斜边上的中线等于斜边的一半。
矩形的定义:有一个角是直角的平行四边形。
矩形的性质:矩形的四个角都是直角;矩形的对角线平分且相等。
AC=BD矩形判定定理: 1.有一个角是直角的平行四边形叫做矩形。
2.对角线相等的平行四边形是矩形。
3.有三个角是直角的四边形是矩形。
菱形的定义:邻边相等的平行四边形。
菱形的性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形的判定定理: 1.一组邻边相等的平行四边形是菱形。
2.对角线互相垂直的平行四边形是菱形。
3.四条边相等的四边形是菱形。
S菱形=1/2×ab(a、b为两条对角线)正方形定义:一个角是直角的菱形或邻边相等的矩形。
正方形的性质:四条边都相等,四个角都是直角。
正方形既是矩形,又是菱形。
正方形判定定理:1.邻边相等的矩形是正方形。
2.有一个角是直角的菱形是正方形。
梯形的定义:一组对边平行,另一组对边不平行的四边形叫做梯形。
直角梯形的定义:有一个角是直角的梯形等腰梯形的定义:两腰相等的梯形。
等腰梯形的性质:等腰梯形同一底边上的两个角相等;等腰梯形的两条对角线相等。
等腰梯形判定定理:同一底上两个角相等的梯形是等腰梯形。
解梯形问题常用的辅助线:如图线段的重心就是线段的中点。
平行四边形的重心是它的两条对角线的交点。
四边形(平行四边形、矩形、菱形、正方形)期中复习知识与技能:掌握平行四边形、矩形、菱形、正方形的有关性质和常用判定方法,灵活运用这些知识进行有关的证明和计算;培养学生阅读的技能,进一步培养和发展学生的逻辑思维能力与推理论证能力。
过程与方法:1、在综合问题解决过程中,学会阅读综合问题的方法,获取有价值的数据的方法;2、经历综合问题的探索过程,学会分析问题的方法。
3、经历一题多解,多题一解,培养学生的发散思维,关注知识间的联系。
情感态度与价值观:1、在问题解决过程中培养学生的数学素养和严谨的科学态度;2、在问题解决过程中,让学生获得成功体验。
教学重点:阅读,对基本图形的认识。
教学难点:审题,寻找解决问题的突破口。
教学过程:一、知识要点回顾:(在复习前提前将表格印好,让学生回家完成)见附件1二、例题讲解:例1:如图,在ABCD 的纸片中,AC ⊥AB ,AC 与BD 交于O ,将△ABC 沿对角线AC翻折得到'AB C ∆.(1)求证:以A 、C 、D 、'B 为顶点的四边形是矩形; (2)若212ABCDScm =, 求翻折后纸片重叠部分的面积,即ACE S ∆.意图:1、平行四边形的性质、矩形的判定定理的综合应用;2、实现一题多解,有选择的运用矩形的判定定理,评析证明方法的优劣。
3、等积变换,以及对三角形底的选择直接影响到求面积的难易程度。
例2:我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称; (2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论. 意图:如何实现构造两条线段之和及将夹角进行有效转移例3:如图,已知ABCD 中,AE 平分BAD ∠,交DC 于E ,DF BC ⊥于F ,交AE 于G ,且DF AD =。
人教版八年级数学下册第18章平行四边形知识要点总结第18章平行四边形复习平行四边形知识点一、平行四边形定义:二、平行四边形的性质边:1.两组对边互相平行且相等;符号语言:角:2.两组对角分别相等;符号语言:对角线:3.对角线互相平分。
符号语言:对称性:中心对称图形但不一定是轴对称图形平行线之间的距离:平行线间的距离都相等符号语言:∵AE∥BF且AB⊥BF,CD⊥BF,EF⊥BF∴AB=CD=EF三、平行四边形的判定边:1. 两组对边分别平行.....的四边形是平行四边形;符号语言:2. 两组对边分别相等......的四边形是平行四边形;符号语言:3. 一组对边平行且相等......的四边形是平行四边形;符号语言:角:4. 两组对角分别相等......的四边形是平行四边形;符号语言:对角线:5.对角线互相平分的四边形是平行四边形;符号语言:四、平行四边形的面积公式S□ABCD=ah(a是边,h是这个边的高);五、与三角形有关的知识点1.三角形中位线定义:连接三角形两边中点的线段..叫做三角形的中位线。
2.三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半符号语言:3.取值范围:利用三角形的性质:两边之和大于第三边;两边之差小于第三边 如:已知□ABCD 两对角线的长分别为6和8,则较短边长x 的取值范围为1<x<7.4.直角三角形性质定理(1)直角三角形斜边上的中线等于斜边的一半.符号语言:∵在Rt △ABC 中,且AD =CD∴ BD=AD=CD(2)直角三角形中,30°角所对应的直角边等于斜边的一半.符号语言:∵在Rt △ABC 中,且∠A=30°∴BC=12AC 或 2BC=AC特殊的平行四边形知识点—矩形一、矩形的定义:二、矩形的性质1.矩形具有平行四边形的所有性质;2.矩形的四个角都是直角; 符号语言:3.矩形的对角线平分且相等。
符号语言:三、矩形判定1.有一个角是直角的平行四边形.....叫做矩形。
八年级下册第十八章平行四边形全章知识点要点一、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.3.面积=4.判定:边:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形.角:(4)两组对角分别相等的四边形是平行四边形;(5)两组邻角分别互补的四边形是平行四边形.边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形;对角线:(7)对角线互相平分的四边形是平行四边形.要点:平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.要点二、矩形1.定义:有一个角是直角的平行四边形叫做矩形.2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.3.面积=4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形.要点:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半.要点三、菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2.性质:(1)具有平行四边形的一切性质;(2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;(4)中心对称图形,轴对称图形.3.面积=4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)四边相等的四边形是菱形.要点四、正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行;(2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积=4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形.二、几种特殊平行四边形的关系三角形中位线定理 : 三角形的中位线平行于第三边, 并且等于第三边的一半。
四边形一、四边形的性质与判定1.定义平行四边形两组对边分别平行的四边形是平行四边形(对角相等、对角线互相平分)矩形有一个角是直角的平行四边形是矩形(对角线相等)菱形有一组邻边相等的平行四边形是菱形(对角线垂直、对角线平分对角)正方形有一个角是直角,有一组邻边相等的平行四边形是正方形2.判定:平行四边形(边3、角1、对角线1)矩形1.两组对边分别平行的四边形是平行四边形。
(定义)2.两组对边分别相等的四边形是平行四边形。
3.一组对边平行且相等的四边形是平行四边形。
4.两组对角分别相等的四边形是平行四边形。
5.对角线互相平分的四边形是平行四边形。
1.有一个角是直角的平行四边形是矩形。
(定义)2.三个角是直角的四边形是矩形。
3.对角线相等的平行四边形是矩形。
其它:对角线相等且互相平分的四边形。
菱形正方形1.有一组邻边相等的平行四边形是菱形。
(定义)2.四边相等的四边形是菱形。
3.对角线互相垂直的平行四边形是菱形。
其它:1对角线垂直且互相平分的四边形是菱形。
2.一条对角线平分一组对角的平行四边形是菱形。
1.有一个角是直角,有一组邻边相等的平行四边形是正方形。
(定义)2.一组邻边相等的矩形是正方形。
3.有一个角是直角的菱形是正方形。
其它:对角线互相平分相等且垂直的四边形是正方形。
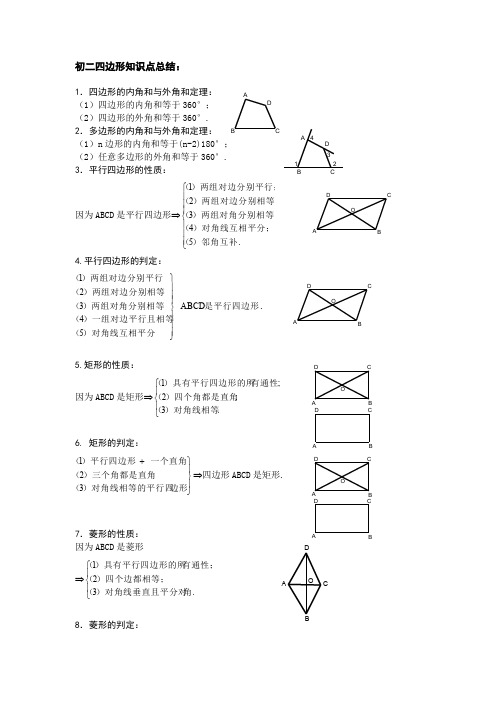
3.知识梳理1.四边形的内角和与外角和定理:(1)四边形的内角和等于360°; (2)四边形的外角和等于360°. 2.多边形的内角和与外角和定理: (1)n 边形的内角和等于(n-2)180°; (2)任意多边形的外角和等于360°. (3) 任意多边形有2)3(-n n 条对角线 3.平行四边形的性质:因为ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;(4.平行四边形的判定:是平行四边形)对角线互相平分()一组对边平行且相等()两组对角分别相等()两组对边分别相等()两组对边分别平行(ABCD 54321⎪⎪⎪⎭⎪⎪⎪⎬⎫.5.矩形的性质:因为ABCD 是矩形⇒⎪⎩⎪⎨⎧.3;2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所(ABDOCABDOCAD BCAD BCOA BCD 12346. 矩形的判定:⎪⎭⎪⎬⎫+边形)对角线相等的平行四()三个角都是直角(一个直角)平行四边形(321⇒四边形ABCD 是矩形.7.菱形的性质:因为ABCD 是菱形⇒⎪⎩⎪⎨⎧.321角)对角线垂直且平分对()四个边都相等;(有通性;)具有平行四边形的所(8.菱形的判定:⎪⎭⎪⎬⎫+边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321⇒四边形四边形ABCD 是菱形.9.正方形的性质:因为ABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角)对角线相等垂直且平(角都是直角;)四个边都相等,四个(有通性;)具有平行四边形的所((1) CDAB(2)A BCDO10.正方形的判定:⎪⎭⎪⎬⎫++++一组邻边等矩形)(一个直角)菱形(一个直角一组邻边等)平行四边形(321⇒四边形ABCD 是正方形.A DBCA DB COCDBAOCDBAOCD AB4、平行四边形、菱形、矩形、正方形的有关性质图形 边角对角线平行四边形 对边平行且相等 对角相等 对角线互相平分菱形 对边平行,四条边相等 对角相等 两对角线互相垂直平分,每一条对角线平分一组对角 矩形对边平行且相等四个角都是直角对角线互相平分且相等 正方形 对边平行、四条边都相等 四个角都是直角两条对角线互相平分、垂直、相等,每一条对角线平分一组对角二、梯形常见的辅助线11.等腰梯形的性质:因为ABCD 是等腰梯形⇒⎪⎩⎪⎨⎧.321)对角线相等(;)同一底上的底角相等(两底平行,两腰相等;)(12.等腰梯形的判定:⎪⎭⎪⎬⎫+++对角线相等)梯形(底角相等)梯形(两腰相等)梯形(321⇒四边形ABCD 是等腰梯形 (1)∵ABCD 是梯形且AD ∥BC ; (2)∵AC=BD ∴ABCD 四边形是等腰梯形 13.三角形中位线定理:三角形的中位线平行第三边,并且等于它的一半.14.梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.ABC DOABCDOEFD ABC1.延长两腰交于一点作用:使梯形问题转化为三角形问题。
朔州市文曲星教育文化培训中心中考四边形与三角形复习要求是,能运用这些图形进行镶嵌,你必须会计算特殊的初中数学四边形,能根据图形的条件把四边形面积等分。
能够对初中数学特殊四边形的判定方法与联系深刻理解。
掌握平行四边形、矩形、菱形、正方形、等腰梯形的概念、性质和常用判别方法,特别是梯形添加辅助线的常用方法.掌握三角形中位线和梯形中位线性质的推导和应用。
会画出四边形全等变换后的图形,会结合相关的知识解题.结合几何中的其他知识解答一些有探索性、开放性的问题,提高解决问题的能力·(一)、平行四边形的定义、性质及判定.1:两组对边平行的四边形是平行四边形.2.性质:(1)平行四边形的对边相等且平行;(2)平行四边形的对角相等,邻角互补;(3)平行四边形的对角线互相平分.3.判定:(1)两组对边分别平行的四边形是平行四边形:(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形:(5)对角线互相平分的四边形是平行四边形.4·对称性:平行四边形是中心对称图形.(二)、矩形的定义、性质及判定.1-定义:有一个角是直角的平行四边形叫做矩形.2·性质:矩形的四个角都是直角,矩形的对角线相等3.判定:(1)有一个角是直角的平行四边形叫做矩形;(2)有三个角是直角的四边形是矩形:(3)两条对角线相等的平行四边形是矩形.4·对称性:矩形是轴对称图形也是中心对称图形.(三)、菱形的定义、性质及判定.1·定义:有一组邻边相等的平行四边形叫做菱形.(1)菱形的四条边都相等;。
(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角(3)菱形被两条对角线分成四个全等的直角三角形.(4)菱形的面积等于两条对角线长的积的一半:s 菱=争6(n、6 分别为对角线长).3.判定:(1)有一组邻边相等的平行四边形叫做菱形(2)四条边都相等的四边形是菱形;(3)对角线互相垂直的平行四边形是菱形.4.对称性:菱形是轴对称图形也是中心对称图形.(四)、正方形定义、性质及判定.'1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.2.性质:(1)正方形四个角都是直角,四条边都相等;(2)正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;(3)正方形的一条对角线把正方形分成两个全等的等腰直角三角形;(4)正方形的对角线与边的夹角是45。
;(5)正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.3.判定:(1)先判定一个四边形是矩形,再判定出有一组邻边相等;(2)先判定一个四边形是菱形,再判定出有一个角是直角.4.对称性:正方形是轴对称图形也是中心对称图形.(五)、梯形的定义、等腰梯形的性质及判定.1.定义:一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.一腰垂直于底的梯形是直角梯形.2.等腰梯形的性质:等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.3.等腰梯形的判定:两腰相等的梯形是等腰梯形;同一底上的两个角相等的梯形是等腰梯形;两条对角线相等的梯形是等腰梯形.4.对称性:等腰梯形是轴对称图形.(六)、三角形的中位线平行于三角形的第三边并等于第三边的一半;梯形的中位线平行于梯形的两底并等于两底和的一半.(七)、线段的重心是线段的中点;平行四边形的重心是两对角线的交点;三角形的重心是三条中线的交点..(八)、依次连接任意一个四边形各边中点所得的四边形叫中点四边形O四边形经典题型1.如果一个四边形内角之比是 2∶2∶3∶5,那么这四个内角中()A.有两个钝角B.有两个直角C.只有一个直角2.一个多边形的外角和是内角和的一半,则它是边形D.只有一个锐角()A.7B.6C.5D.43.若多边形的每个内角都为 150°,则从一个顶点引的对角线有()A.7 条B.8 条C.9 条D.10 条14.一个多边形的内角和是外角和的2 2倍,则边数是()A.14B.7C.21D.105. 一个多边形的每个内角都等于 144°,这个多边形的边数是( )A.8B.9C.10D.116. ∠A 的两边分别垂直于∠B 的两边,且∠A 比∠B 大 60°,则∠A 等于 ()A.120°B.110°C.100°D.90°7. 若等角 n 边形的一个外角不大于 40°,则它是边形()A.n=8B.n=9C.n >9D.n≥92 8. 每个内角都相等的多边形,它的一个外角等于一个内角的 ,则这个多边形是边形.39. 两个多边形的边数之比为 1∶2,内角和的度数之比为 1∶3,求这两个多边形的边数.10. 已知线段 AC=8,BD=6。
(1) 已知线段 AC 垂直于线段 BD 。
设图 13―1、图 13―2 和图 13―3 中的四边形 ABCD 的面积分别为 S 1、S 2 和 S 3,则 S 1=,S 2= ,S 3= ;ABDC图13-4(2) 如图 13―4,对于线段 AC 与线段 BD 垂直相交(垂足 O 不与点 A ,C ,B ,D 重合)的任意情形,请你就四边形 ABCD 面积的大小提出猜想,并证明你的猜想;(3) 当线段 BD 与 AC (或 CA )的延工线垂直相交时,猜想顺次连接点 A ,B ,C ,D ,A 所围成的封闭图形的面积是多少?经典1:如图,平行四边形ABCD 中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:∠BAE =∠DCF.经典 2:如图,在□ABCD 中,O 是对角线 AC 和 BD 的交点,OE⊥AD 于 E,OF⊥BC 于 F.求证:OE=OF.经典3:如图,在平行四边形ABCD 的各边AB、BC、CD、DA 上,分别取点K、L、M、N,使AK=CM、BL=DN,求证:四边形KLMN 是平行四边形.经典4:已知如图:在平行四边形ABCD 中,延长AB 到E,延长CD 到F,使BE=DF,则线段AC 与EF 是否互相平分?说明理由.注意:其他还有一些判定平行四边形的方法,但都不能作为定理使用。
如:“两组对角分别相等的四边形是平行四边形”,它显然是一个真命题,但不能作为定理使用.EFO经典 5:如图,矩形 ABCD 中,AC 与 BD 交于 O 点,BE ⊥AC 于 E,CF ⊥BD 于 F.AD求证:BE = CF.BC经典 6:如图,在△ABC 中,AB=AC,D 为 BC 中点,四边形 ABDE 是平行四边形. 求证:四边形 ADCE 是.经典练习:1. 平行四边形 ABCD 的周长 32,5AB=3BC,则对角线 AC 的取值范围为()A.6<AC<10B.6<AC<16C.10<AC<16D.4<AC<16 2. 如图,在平行四边形 ABCD 中,下列各式不一定正确的是()A. ∠1+ ∠2 = 1800B. ∠2 + ∠3 = 1800C. ∠3 + ∠4 = 1800D. ∠2 + ∠4 = 18003. 如图,在平行四边形 ABCD 中,E 是 AD 上一点,连结 CE 并延长交 BA 的延长线于点F,则下列结论中错误的是()A.∠AEF=∠DECB.FA:CD=AE:BCC.FA:AB=FE:ECD.AB=DC4.如图,在□ABCD中,对角线AC,BD 相交于点O,E,F 是对角线AC 上的两点,当E,F 满足下列哪个条件时,四边形DEBF 不一定是平行四边形()A.AE=CFB.DE= BFC.∠ADE=∠CBFD.∠AED=∠CFB5.如图,ABCD 中,点 E 在边AD 上,以 BE 为折痕,将△ABE向上翻折,点 A 正好落在CD 上的点F,若△FDE的周长为8,△FCB的周长为22,则FC 的长为_ 。
6.已知:□ABCD中,AE 平分∠DAB交DC 于E,BF 平分∠ABC交DC 于F,DC=8cm,AD=3cm,求DE、DF 与FC 的长.7.如图,在ABCD 中,对角线AC 与BD 交于点O,已知点E、F 分别为AO、OC 的中点,证明:四边形BFDE 是平行四边形.8.已知:□ABCD中的对角线 AC、BD 相交于 O,M 是AO 的中点,N 是C O 的中点,请问:BM 与DN 有什么关系?9.如下图,平行四边形 ABCD 中,E、F 分别是 AB、CD 的中点,AF 与DE 交于点 G,CE 与BF 交于点 H,问:图中还有哪些平行四边形?请证明你的结论.B G_10. 如图,在格点图中,以格点 A 、B 、C 、D 、E 、F 为顶点,你能画出多少个平行四边形?试在图中画出来.11. 如图,在△ABC 中,D 、E 分别是 AB 、AC 的中点,F F 是E DE 延长线上的点,且 EF=DE ,则图中的平行四边形有哪些?说说你的理由.DC12. 已知任意四边形 ABCD ,且线段 AB 、BC 、CD 、DA 、AC 、BD 的中点分别是 E 、F 、G 、H 、P 、Q .(1) 若四边形 ABCD 如图①,判断下列结论是否正确(正确的在括号里填“√”,错误的在括号里填“×”).甲:顺次连接 EF 、FG 、GH 、HE 一定得到平行四边形;( ) 乙:顺次连接 EQ 、QG 、GP 、PE 一定得到平行四边形.()(2) 请选择甲、乙中的一个,证明你对它的判断.(3) 若四边形 ABCD 如图②,请你判断(1)中的两个结论是否成立?AED13. 直角三角形斜边上的高与中线分别是 5cm 和 6cm,则它的面积为 FC14. 如图,矩形纸片 ABCD,长 AD =9cm,宽 AB =3 cm,将其折叠,使点 D 与点 B 重合,那么折叠后 DE 的长和折痕 EF 的长分别11OEO3 3为和 。
15. 矩形的较长边为 6,两条对角线的交角为 60°,则矩形的周长是()A.18B.12+4C.12+2D.2416. 如图,在矩形 ABCD 中,AB=3,AD=4,点 P 在 AD 上,PE ⊥AC于 E,PF ⊥BD 于 F,则 PE+PF 等于( ) 7 12 13 14 A DA.B.C.D.555517. 如图,矩形 ABCD 的周长为 20cm,两条对角线相交于点 O,过点 O 作 AC 的垂线 EF,分别交 AD 、BC 于 E 、F 点,连接 CE ,则△CDE 的周长为()BFCA. 5cmB.8cmC.9cmD.10cm18. 如图,在矩形 ABCD 中,AC 、BD 相交于 O,AE 平分∠BAD,交 BC 于 E,若∠CAE=15°,求∠BOE 的度数.19. 已知:如图,在ABCD 中,以 AC 为斜边作 Rt△ACE,且∠BED 为直角.求证: 四边形 ABCD 是矩形.ADBCE20、如图,四边形 ABCD 中,AB ∥CD ,AC 平分∠BAD ,CE ∥AD 交 AB 于 E . (1) 求证:四边形 AECD 是菱形;(2) 若点 E 是 AB 的中点,试判断△ABC 的形状,并说明理由.。