手把手教你怎么用UDS解自己的方程

第九章本章扼要介绍了FLUENT中用户自定义标量及它们的用法。

•9.1 介绍•9.2 理论•9.3 UDS的定义，求解，后处理9.1 介绍FLUENT可以用求解诸如质量组分之类标量方程的相同方法来求解任意的用户自定义标量 (UDS)。

在某些类型的应用中，如燃烧模拟或是等离子增强表面反应（plasma-enhanced surface reaction）的模拟中，还需引入新的标量输运方程。

用户自定义标量可被用于磁流体动力(MHD)模拟中。

在MHD中，导电流体（conducting fluid）的流体将会产生磁场，此磁场可以用户自定义标量来求解。

磁场造成的对流体的阻尼（a resistance to the flow），可用用户自定义的源项来模拟。

书中4.3.12和4.3.13介绍了用 UDFs来定义标量输运方程的例子。

to customize scalar transport equations.9.2 理论对于一个任意的标量， FLUENT 可求解方程(9.2.1)此处 和 是用户为N 个标量方程中的每一个方程定义的扩散系数和源项。

对于稳态的情况，根据计算对流通量的方法的不同，FLUENT 可求解以下的三种方程之一：•如果对流通量不用计算，则FLUENT 可解方程(9.2.2)此处 和 是用户为N 个标量方程中的每一个方程定义的扩散系数和源项。

•如果以质量流率来计算对流通量，FLUENT可解方程(9.2.3)•如果选择一个用户自定义函数来计算对流通量，FLUENT可解方程(9.2.4)此处 是用户定义的流率。

!! 在FLUENT中，用户自定义函数只可在流体区域内求解，而不能在固体区域内求解。

9.3 UDS的定义，求解，后处理定义，求解，后处理用户自定义标量的步骤概括如下。

注意UDFs 在多相流体和单项流体中应用的重要不同在于，如果是单相的情况（an individual phase）， 用户需要提供用户自定义的标量通量函数。

【教程】用计算器解方程（牛顿法）很多计算器都自带利用标准式解方程的功能，解方程式,需要手动输入abc的值。

但这样往往需要化简出abc到底是多少，这样容易计算错误，还加大了计算量，往往在注册考试中不实用。

下面我介绍一个直接的方法，无需化简公式，就可以解出结果的方法。

二、利用此方法的好处可解决所有公式变形问题，利用牛顿法解方程，一元方程可直接出结果，一元多次方程无需化简成标准形式，直接求解，大大节省化简、变形公式时间。

提高做题效率，解决重复简单计算的厌恶感。

提高做题准确率。

三、牛顿法解方程具体步骤1、你的计算器是否有此功能大多数科学计算器都长的差不多，但是考友们手里的计算器是否有该功能那就不一走了。

无论是手算解方程还是计算器自动解方程”只要是方程”就有两个必不可少的元素："等号二〃” 〃未知数X"。

以卡西欧fx-991es plus型号计算器举例，此型号计算器如图所示。

只要带〃等号二〃、〃未知数x〃的科学计算器z就有解方程功能。

需要注意的是z这里说的〃等号二〃并不是如图所示右下角的〃二〃，而是左上角那个红色的〃二〃。

细心的同学会发现，黄色的1号上档键SHIFT ,对应的都是标志有黄色字体的功能；红色的2号上档键ALPHA ,对应的都是标志有红色字体的功能。

nUS2号上档键|J 加gin(X)dH12.070346321号上档健方程中的等号方程中的未知数X5 16常规等号,相当于电脑中的回车键元一次方程。

而我们只需要把方程输入到计算器中,即可解出X。

具体输入方法如下:(1 )按数字"5〃(2 )按〃2号上档键〃z再按’方程中的未知数x键〃。

即：红色的ALPHA和白色的右半边括号。

这样我们就输入了未知数x(3 )按，再按〃9〃(4 )按〃2号上档键〃，再按〃方程中的等号键"。

即：红色的ALPHA和白色的CALC。

这样我们就输入了〃二〃3、解方程做到这里,我们的方程就已经输入好了。

手把手教你怎么用UDS解自己的方程所谓UDS，就是用户自定义标量方程，这类方程大致表达式如下：依次为时间项，对流项，扩散项，源项。

当然其中有可能有些不同，不过只要是对流扩散型的方程，都可以用UDS来解（前面有人讨论只包含对流而没有扩散的方程用UDS来解的例子，不过效果据说不好：），跳过）。

与标准对流扩散方程多出来的部分，都可以写到SOURCE（源项）里面。

以下解一个如下的POSSION方程为例，来介绍一下整个UDS求解的流程：1：准备工作将方程与UDS标准方程对比，发现没有时间项，对流项，同时多出一项，我们将方程化为标准形式，可以看出该项可作为源项来处理。

即：该源项用UDF加入到求解方程中，调用的宏为DEFINE_SOURCE，具体参见帮助的相关章节，这里该UDF可写为：#include "udf.h"DEFINE_SOURCE(uds_source,c,t,dS,eqn){real x[ND_ND];real source;C_CENTROID(x,c,t);source=-sin(C_UDSI(c,t,0));dS[eqn]=-cos(C_UDSI(c,t,0));return source;}其中的dS[eqn]是source的剃度，用来加快收敛。

2：设置UDS准备工作完成，现在启动FLUENT，先读入CAS文件，编译连接好该UDF文件。

然后，如下图所示操作，点开，出现将UDS项由0加到1，如下图：底下FLUX FUNCTION是对应对流项设置的，由于其中我们的POSSION方程没有对流项，所以选择NONE，点击OK，UDS加入成功，出现如下图的提示，提醒UDS加入了，是否需要修改UDS扩散系数，点击OK进入材料面版，可以看见底下的UDS属性，点击EDIT，由于PISSION方程前面没有系数，所以定义扩散系数为1。

3：边界条件设置进入边界条件面版，首先是加入前面设置的源项，如下图：然后是WALL边界等的UDS边界条件设置，这里有标量值以及流通量两个选项，根据需要选择。

用高斯消元法解线性方程组高斯消元法是一种常用的解线性方程组的方法。

它通过一系列的行变换将线性方程组转化为一个简化的行阶梯形式，从而可以方便地求解方程组。

基本步骤使用高斯消元法解线性方程组的基本步骤如下：1. 构造增广矩阵：将线性方程组的系数矩阵和常数向量按照方程的顺序组合成一个增广矩阵。

2. 初等行变换：通过初等行变换操作，将增广矩阵转化为行阶梯形或行最简形。

3. 回代求解：从最后一行开始，反向代入得到方程组的解。

详细步骤以下是用高斯消元法解线性方程组的详细步骤：1. 将线性方程组的系数矩阵和常数向量按照方程的顺序组合成一个增广矩阵，如下所示：[a11 a12 ... a1n | b1][a21 a22 ... a2n | b2][... ... ... ... | ...][an1 an2 ... ann | bn]2. 选择第一个非零元素所在的列，记为第 k 列。

3. 通过初等行变换操作，将第 k 列除了第 k 行之外的所有元素变为零。

首先，将第 k 行的第 k 个元素系数标准化为 1，即将第 k 行的所有元素除以第 k 个元素的值。

然后，对第 i 行（i ≠ k）进行以下操作：将第 i 行的第 k 个元素的系数变为零，即将第 i 行减去第 k 行的 k 个元素乘以第 i 行的第 k 个元素的系数。

4. 重复步骤 2 和步骤 3，直至所有列都处理完毕。

5. 如果最后一行的所有元素都为零，则该线性方程组无解。

6. 如果最后一行的最后一个非零元素所在的列号为 m，则 m+1 到 n 列的所有元素均为自由变量。

7. 从最后一行开始，反向代入求解自由变量。

示例假设有以下线性方程组：2x + 3y - z = 13x + 2y + z = 2x + 3y + 2z = 3将该方程组转化为增广矩阵的形式：[2 3 -1 | 1][3 2 1 | 2][1 3 2 | 3]通过高斯消元法的步骤，可以得到以下的行阶梯形式：[1 3/2 1/2 | 3/2][0 7/2 -3/2 | -3/2][0 0 17/7 | 17/14]根据行阶梯形式，可以得到方程组的解为：x = 1/2y = -1/2z = 2/7总结高斯消元法是一种简单而有效的方法，用于解线性方程组。

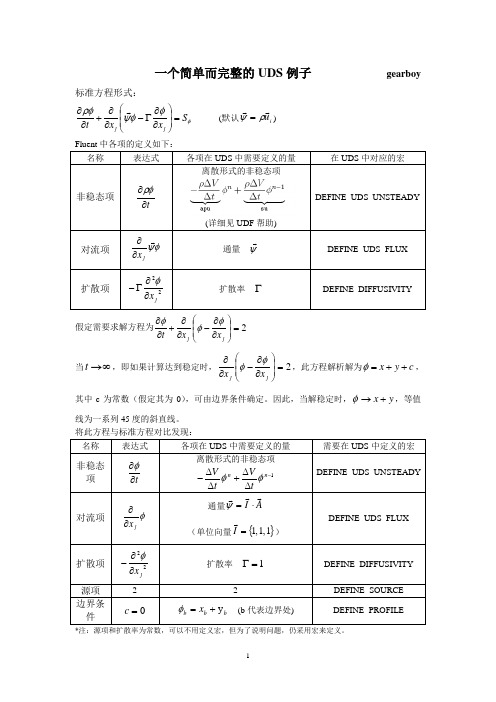
一个简单而完整的UDS 例子 gearboy标准方程形式：φφφψρφS x x t j j =⎪⎪⎭⎫ ⎝⎛∂∂Γ-∂∂+∂∂ (默认i u ρψ=) Fluent 中各项的定义如下： 名称表达式各项在UDS 中需要定义的量在UDS 中对应的宏非稳态项t∂∂ρφ离散形式的非稳态项(详细见UDF 帮助)DEFINE_UDS_UNSTEADY 对流项φψ jx ∂∂ 通量 ψDEFINE_UDS_FLUX扩散项22jx ∂∂Γ-φ扩散率 ΓDEFINE_DIFFUSIVITY假定需要求解方程为2=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+∂∂j jx x t φφφ 当∞→t ，即如果计算达到稳定时，2=⎪⎪⎭⎫⎝⎛∂∂-∂∂j jx x φφ，此方程解析解为c y x ++=φ，其中c 为常数（假定其为0），可由边界条件确定。

因此，当解稳定时，y x +→φ，等值线为一系列45度的斜直线。

将此方程与标准方程对比发现： 名称表达式各项在UDS 中需要定义的量需要在UDS 中定义的宏 非稳态项t ∂∂φ 离散形式的非稳态项1-∆∆+∆∆-n n tV t V φφ DEFINE_UDS_UNSTEADY对流项φjx ∂∂ 通量A I ⋅=ψ（单位向量{}1,1,1=I） DEFINE_UDS_FLUX扩散项 22jx ∂∂-φ扩散率 1=ΓDEFINE_DIFFUSIVITY 源项22DEFINE_SOURCE 边界条件0=cb b b x y +=φ (b 代表边界处)DEFINE_PROFILE*注：源项和扩散率为常数，可以不用定义宏，但为了说明问题，仍采用宏来定义。

假定如图所示的计算域，其中正方形边长为10，原点在正方形中心，四边均为wall。

将如下源码，写入一个UDF文件，例如MyFistUDF.c，与cas文件放在同一目录。

#include "udf.h"DEFINE_UDS_UNSTEADY(MyUnsteady,c,t,i,apu,su){real physical_dt, vol, phi_old;physical_dt = RP_Get_Real("physical-time-step");vol = C_VOLUME(c,t);*apu = -vol / physical_dt; /*implicit part*/phi_old = C_STORAGE_R(c,t,SV_UDSI_M1(i));*su = vol*phi_old/physical_dt; /*explicit part*/}DEFINE_UDS_FLUX(MyFlux,f,t,i){real NV_VEC(unit_vec), NV_VEC(A); //声明矢量变量F_AREA(A, f, t);NV_DS(unit_vec, =, 1, 1, 1, *, 1); //单位矢量赋值return NV_DOT(unit_vec, A); //矢量点积}DEFINE_DIFFUSIVITY(MyDiff,c,t,i){return 1.0;}DEFINE_SOURCE(MySource,c,t,dS,eqn){dS[eqn]=0;return 2.0;}DEFINE_PROFILE(MyProfile,thread,index) {real x[ND_ND]; /* this will hold the position vector */ real xx,yy; face_t f;begin_f_loop(f,thread) {F_CENTROID(x,f,thread); xx = x[0]; yy=x[1];F_PROFILE(f,thread,index) = (xx+yy); //b b b x y +=φ }end_f_loop(f,thread) }编译通过并载入启动非稳态求解器，并在Define-User-Defined-Scalars 面板中添加一个UDS ，选择自定义的通量和非稳态项在材料面板中，选择自定义扩散率在boundary conditions的Fluid面板中，选择自定义源项在boundary conditions的壁面边界条件面板中，选择自定义边界条件在solve-controls-solution中禁止Flow计算，只计算自定义标量迭代过程中的残差曲线，可以看出正逐渐趋向稳定采用后处理等值线面板，观察自定义标量的等值线未完全稳定时的等值线最终稳定时的等值线，可以看出是一系列45度的斜直线，与解析解相同。

1. 资料:(1)空气龄计算的输运方程:数值计算方法是根据示踪气仿的质量守恒方程.得到其质量液度输运方程, 然后根据示踪汽耶法，匚以推导岀空气龄的输运方程’卅胳)+別页(T式中u,v T w分别为三个坐标轴方向的速度；T为扩散系数「从上式可以看岀，空气龄勻痂动和扩散系数有关.方程形式与连续性方程、动量方程、湍济模型方程相同3有了空气龄喻运方程，就可以来用数值计算方法对空气龄进行求解9(2 ) flue nt中求解空气龄UDS程序: #in elude "udf.h"#in elude "prop.h"DEFINE_DIFFUSIVITY(mean_age_diff, e, t, i){return C_R(c,t)*2.88e-05+C_MU_EFF(c,t)/0.7;}DEFINE_SOURCE(mean_age_source, c, t, dS, eqn){dS[e qn ]=0;return C_R(c,t);}2. 操作流程1) 打开case和data文件2) 编译UDF文件，将上面的UDS求解程序保持为C文件格式的文件，可以采用define ——user-defi ned functions interpered 或是compile 的方式编译UDF文件。

Source Mile Hams匚：出 en ^wnden c 快 sktop \2Q 141CPF Cnrnmand Norrie CPP Stade Size110000V▼Q Display Assembly Listing [:U SE Contrisuted CPPUser-Defined ScalarsNumber of Usa--DefTiad Scakrs i亠I! -- IsH Inlet DifftisonUse r -Define d Scalar 営 Option 蛊UDE Index 冠丄Interpreted UDF,In terpretClose I Help3）设置UDS 参数。

⽤户⾃定义标量⽅程（UDSTransportEquations）⽤户指导部分9 基本流体流动模型9.1 ⽤户⾃定义标量⽅程(UDS Transport Equations)9.1.1 介绍ANSYS FLUENT 能够解决任意的传输⽅程(transport equation)，同样的，⽤户⾃定义标量(UDS) 能够解决⼀个标量(scalar)的传输⽅程，如某种物质的质量分数(species mass fraction)。

通常，在诸如等离⼦增强表⾯反应模型等特定燃烧情形中，可能会⽤到额外的标量传输⽅程。

ANSYS FLUENT 允许你在User-Defined Scalar 的对话框⾥定义附加的标量传输⽅程。

9.1.2 UDS 理论9.1.2.1 单相流对任意的标量?k，ANSYS FLUENT 能够解决下述⽅程：eρ?k et +eex i(ρu i?k?Γke?kex i)=S?k k=1,…,N(Equ.9.1- 1)上式中，Γk和S?k分别代表⽤户所定义的N个标量⽅程中某⼀个标量⽅程的扩散系数和源项。

注意到Γk应该被定义为⼀个各向异性的张量系数，所以扩散项的表达式应为??(Γk??k)。

如果扩散是各向同性的，则扩散系数Γk能够写成Γk I的形式，其中，I是Γk I的特征矩阵。

对于稳态问题(steady-state)，依据对对流项(convective flux)的不同处理⽅式，ANSYS FLUENT 会解决下述三个标量⽅程中的⼀种。

情形1，不考虑对流项。

ANSYS FLUENT 将会解决下述⽅程：eex i (Γke?kex i)=S?k k=1,…,N(Equ.9.1- 2)情形2，依据质量流率来计算对流项。

ANSYS FLUENT 将会解决下述⽅程：eex i (ρu i?k?Γke?kex i)=S?k k=1,…,N(Equ.9.1- 3)情形3，使⽤⽤户⾃定义函数(user-defined function)功能⾃定义对流项的计算⽅式。