傅里叶变换的性质及常用函数的傅里叶变换
- 格式:docx
- 大小:2.31 MB
- 文档页数:3
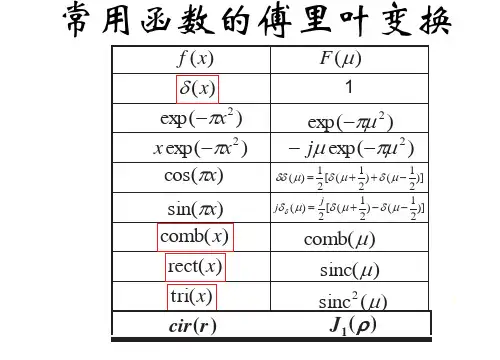

常用傅立叶变换表
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
18
δ(ω) 代表分布. 这个变换展示了狄拉克δ函数的重要性:该函数是常函数的傅立叶变换
19 变换23的频域对应
20 由变换3和24得到.
21
由变换1和25得到,应用了:
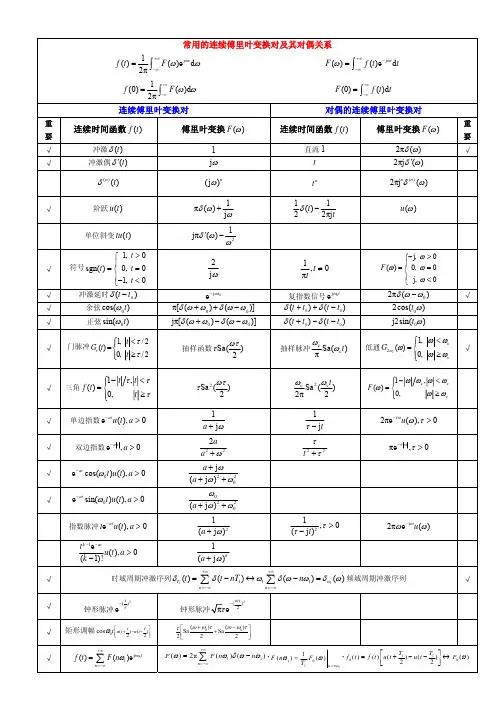
时域信号
弧频率表示的 傅里叶变换
注释
1线性
2 时域平移
3 频域平移, 变换2的频域对应
4
如果
值较大,则
会收缩到
原点附近,而会扩散并变得扁平. 当 | a | 趋向无穷时,成为 Delta 函数。
5 傅里叶变换的二元性性质。
通过交换时域变量 和频域变量 得到. 6 傅里叶变换的微分性质 7 变换6的频域对应 8 表示 和 的卷积 — 这就是 9
和归一化的 10 变换10的频域对应。
矩形函数是理想的低通滤波器,是这类滤波器对冲击的响应。
11
tri 是 12 变换12的频域对应 13 exp( αt 2) 的傅里叶变换是他本身. 只有当 Re(α) > 0时,这是可积的。
14
15
16 a>0
17
变换本身就是一个公式。



广义Fourier 变换:函数不严格满足存在条件,但是函数可定义另一函数 所组成的序列的极限,序列中的函数有F.T.;对组成序 列的每一个函数进行变换,就产生一个相应的变换序 列,该新序列的极限即为原函数的广义F.T.g ( x, y ) = lim f N ( x, y ) ℑ{ f N ( x, y )} = FN ( f x , f y )N →∞ N →∞lim FN ( f x , f y ) = ℑ{ g ( x, y )} = G ( f x , f y )ℑ{δ ( x, y )}lim ℑ{ N exp(−N π (x + y ))} = limexp(−2 2 2 2 N→∞π ( f x2 + f y 2 )2N→∞N fy ⎫ ⎧ 1 fx 1 2 lim ℑ{ N rect(Nx)rect(Ny)} = lim ⎨N ⋅ sin c( )N ⋅ sin c( )⎬ =1 N→∞ N→∞ N N N ⎭ ⎩ N fy ⎫ ⎧ 1 fx 1 lim ℑ{ N sin c(Nx)sin c(Ny)} = lim ⎨N ⋅ rect( )N ⋅ rect( )⎬ =1 N→∞ N→∞ N N N ⎭ ⎩ N2) =1δ−function Properties 1. 筛选性(定义性质)∞ −∞∫ g ( x)δ ( x − x ) dx = g ( x )0 0δ ( x − x0 ) = 0, x ≠ x02. 尺度缩放性质δ (ax) =3. 偶函数x 1 1 δ ( x), δ (ax − x0 ) = δ ( x − 0 ) a a aδ ( x ) = δ ( − x ) , δ ( − x + x 0 ) = δ ( x − x0 )3. 乘积性质g ( x)δ ( x − x0 ) = g ( x0 )δ ( x − x0 ); xδ ( x − x0 ) = x0δ ( x − x0 )4. 积分性质∞−∞∫ Aδ ( x − x ) dx = A0∞−∞∫ δ ( x − x ) dx = 105. 卷积性质g ( x) ∗ δ ( x − x0 ) = g ( x − x0 )卷积定义∞f ( x) ∗ h( x) =−∞∫ f (a)h(x − a)da反转,平移,相乘,积分卷积在光学中的应用卷积表示一输出,在光学上就表示成像系统的像分 布 ;对于线性空间不变光学系统,其输出的信息可 表示为输入信息g与系统脉冲响应函数h(系统对点 源的响应)的卷积 的响应x0处点源:I 0 Δξ 对应的像强度分布P( xi − x0 )输出像:I i ( xi ) = I 0 Δξ P ( xi ) + I 0 Δξ P( xi − ξ 1 ) +KΔξ → 0:I i ( xi ) = ∫ I 0 (ξ ) P( xi − ξ )d ξ二维:g(x, y)表示物(输入信息); h(x,y)表示系统对点源的响应(点扩散函数、脉冲响应函数)输出=g( x, y ) ∗ h(x,y)卷积的性质1. 符合交换律g ( x,y ) ∗ h( x, y ) = h( x, y ) ∗ g ( x,y )2.函数平移不变性f ( x, y ) ∗ h ( x, y ) = g ( x, y ) ↔ f ( x − x0 , y − y0 ) ∗ h( x, y ) = g ( x − x0 , y − y0 )3. 线性运算(af + bh) ∗ g = af ∗ g + bh ∗ g4.δ函数的卷积f ( x, y )* δ ( x, y ) = f ( x, y )δ 函数与任何函数卷积仅重新产生该函数严格再生 5. 光滑作用脉冲响应函数h是 对光学系统性能的 定量评价。
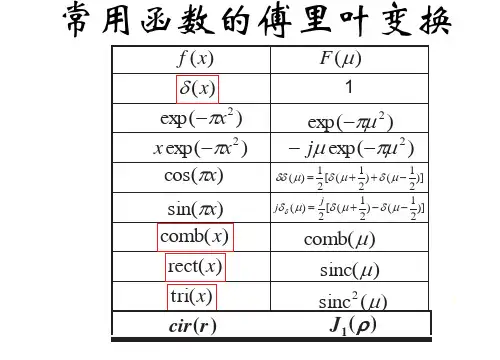

傅里叶变换的性质这里主要介绍二维离散傅里叶变换(DFT ,discrete FT )中的几个常用性质(可分离线、周期性和共轭对称性、平移性、旋转性质、卷积与相关定理):可分离性二维离散傅立叶变换DFT 可分离性的基本思想是二维DFT 可分离为两次一维DFT 。
因此可以用通过计算两次一维的FFT 来得到二维快速傅立叶变换FFT 算法 。
根据快速傅里叶变换的计算要求,需要图像的行列数均满足2的n 次,如果不满足,在计算FFT 之前先要对图像补零以满足2的n 次。
一个M 行N 列的二维图像f(x,y),先按行对列变量y 做一次长度为N 的一维离散傅里叶变换,再将计算结果按列向对变量x 做一次长度为M 傅里叶变换就可以得到该图像的傅里叶变换结果,如下式所示:()()()()∑∑-=-=-⎥⎥⎦⎤⎢⎢⎣⎡-=10102exp 2exp ,1,M x N y M ux j N vy j y x f MN v u F ππ 将上式分解开来就是如下两部分,首先得到F(x,v)再由F(x,v)得到F(u,v):∑-=-=-=101...10]/2exp[),(1),(N y N v N vy j y x f N v x F ,,,π∑-=-=-=101,...,1,0,]/2exp[),(1),(N x M v u M ux j v x F M v u F πu=0,1,2,…M-1;v=0,1,2,...N-1计算过程如下图所示:每一行有N 个点,对每一行的一维N 点序列进行离散傅里叶变换得到F(x,u),再对得到F(x,u)按列向对每一列做M 点的离散傅里叶变换,就可以得到二维图像f(x,y)的离散傅里叶变换F(u,v)同样,做傅里叶逆变换时,先对列向做一维傅里叶逆变换,再对行做一维逆傅里叶变换,如下式所示:()()()()∑∑-=-=⎥⎦⎤⎢⎣⎡=10102exp 2exp ,,M u N v M ux j N vy j v u F y x f ππ x=0,1,2,…M-1;y=0,1,2,...N-1周期性和共轭对称性由傅里叶变换的基本性质可以知道,离散信号的频谱具有周期性。


导数与函数的傅里叶级数与变换导数是微积分中的重要概念之一,而函数的傅里叶级数与变换则是数学中处理周期性函数和信号的工具。
本文将探索导数与函数的傅里叶级数与变换之间的关系和应用。
一、导数的定义与性质导数是用来描述函数的变化率的概念。
对于函数f(x),在某个点x 处的导数可以通过以下定义计算得到:f'(x) = lim(h->0) [f(x+h) - f(x)] / h其中,lim表示极限,h表示变化的量。
导数表征了函数在该点的切线斜率,通过导数可以推导出函数的极值、凹凸性以及函数图像的性质。
在计算导数时,可以利用基本导数公式和导数的性质。
例如,对于常数函数f(x) = c,其导数恒为0;对于多项式函数f(x) = ax^n,其导数为f'(x) = anx^(n-1);另外,导数满足导数的和差法则和导数的乘法法则等性质。
二、函数的傅里叶级数傅里叶级数是一种用三角函数的无限级数表示周期性函数的方法。
周期为T的周期性函数f(x)可以表示为如下的傅里叶级数形式:f(x) = a0/2 + Σ(an*cos(nωx) + bn*sin(nωx))其中,an和bn为傅里叶系数,nyω为频率,n为正整数。
傅里叶级数展开将周期函数转化为一系列三角函数的叠加,通过调整n的取值,可以逐渐逼近原函数的形状。
三、函数的傅里叶变换函数的傅里叶变换是将一个非周期函数表示为连续频谱的方法。
对于函数f(x),其傅里叶变换F(w)定义如下:F(w) = ∫[f(x) * e^(-iwx)]dx在傅里叶变换中,w表示频率,-i表示虚数单位。
通过傅里叶变换,可以将一个函数转化为频率域上的复数函数,从而实现对函数的频谱分析。
傅里叶变换具有线性性质和平移性质。
对于函数的线性组合,其傅里叶变换等于各个函数傅里叶变换的线性组合;对于函数的平移和伸缩,其傅里叶变换也会相应地发生平移和伸缩。
四、导数与傅里叶级数的关系在一定条件下,函数的导数与其傅里叶级数存在一定的关系。
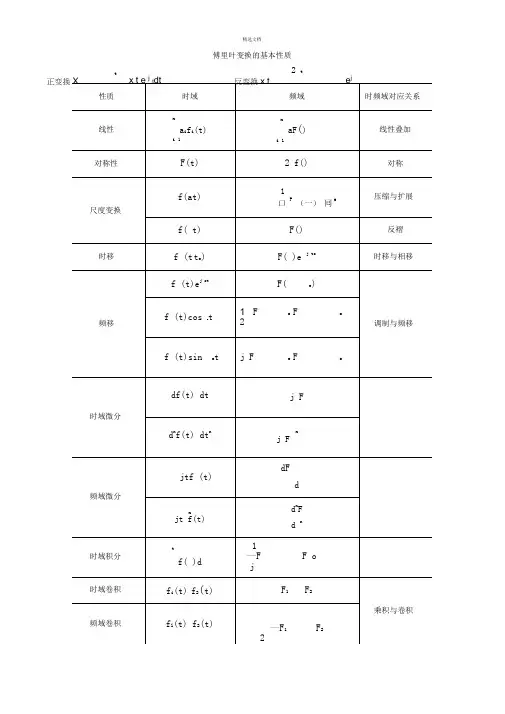
一、三角函数基本公式1. 正弦函数(sin)的定义:在单位圆上,角θ的终边与x轴的交点横坐标为sinθ。
1)反正弦函数(arcsin):y = arcsin(x) ⇔ sin(y) = x,定义域为[-1, 1],值域为[-π/2, π/2]。
2)余弦函数(cos)的定义:在单位圆上,角θ的终边与x轴的交点纵坐标为cosθ。
1)反余弦函数(arccos):y = arccos(x) ⇔ cos(y) = x,定义域为[-1, 1],值域为[0, π]。
3)正切函数(tan)的定义:在单位圆上,角θ的终边与x轴的交点横坐标与纵坐标的比值为tanθ。
1)反正切函数(arctan):y = arctan(x) ⇔ tan(y) = x,定义域为(-∞, +∞),值域为(-π/2, π/2)。
二、傅里叶级数与傅里叶变换1. 傅里叶级数公式:任意周期为2π的函数f(x)可展开为正弦和余弦函数的和。
f(x) = a0 + Σ(an*cos(nx) + bn*sin(nx)),式中,a0为直流分量,an 和bn为交流分量。
1)a0 = (1/2π) * ∫[0, 2π] f(x) dx,an = (1/π) * ∫[0, 2π] f(x) *cos(nx) dx,bn = (1/π) * ∫[0, 2π] f(x) * sin(nx) dx。
2. 傅里叶变换公式:非周期信号f(t)经过连续傅里叶变换得到频谱F(ω)。
F(ω) = ∫[-∞, +∞] f(t) * e^(-iωt) dt。
1)逆傅里叶变换:F(ω)经过逆变换得到原信号f(t)。
f(t) = (1/2π) * ∫[-∞, +∞] F(ω) * e^(iωt) dω。
三、常用傅里叶变换公式1. 矩形脉冲信号:f(t) = rect(t/T)。
1)F(ω) = T * sin(ωT) / (ωT),其中,sinc(u) = sin(u) / u。
2. 三角形脉冲信号:f(t) = tri(t/T)。
傅里叶变换方法1. 傅里叶变换的概念傅里叶变换是一种数学工具,用于将一个函数或信号表示为一系列振幅和相位的复指数函数的和。
它可以将时域中的信号转换为频域中的信号,从而揭示出信号包含的频率成分和它们之间的关系。
傅里叶变换方法是由法国数学家约瑟夫·傅里叶在19世纪初提出的,他认为任何周期性函数都可以用一组正弦和余弦函数来表示。
这个思想被广泛应用于物理、工程、计算机科学等领域,成为了现代科学研究中不可或缺的工具。
2. 傅里叶级数与傅里叶变换傅里叶级数是指将一个周期函数表示为正弦和余弦函数的无穷级数。
它在周期性信号处理中得到广泛应用。
对于一个周期为T、连续可积的函数f(t),其傅里叶级数定义如下:f(t)=a02+∑(a n cos(2πnTt)+b n sin(2πnTt))∞n=1其中,a0、a n和b n是系数,可以通过函数f(t)的积分计算得到。
而傅里叶变换则是将非周期函数表示为连续频谱的积分形式。
对于一个连续可积的函数f(t),其傅里叶变换定义如下:F(ω)=∫f∞−∞(t)e−jωt dt其中,ω是频率,F(ω)表示函数f(t)在频率域中的表示。
3. 傅里叶变换的性质傅里叶变换具有许多重要的性质,这些性质使得它成为一种强大而灵活的工具。
以下是一些常见的傅里叶变换性质:•线性性质:傅里叶变换具有线性性质,即对于任意常数a和b以及两个函数f(t)和g(t),有F(af(t)+bg(t))=aF(f(t))+bF(g(t))。
•平移性质:如果将函数在时域上平移,则其在频域上也会相应平移。
具体而言,如果f(t)经过时移得到ℎ(t)=f(t−t0),那么它们的傅里叶变换满足H(ω)=F(ω)e−jωt0。
•尺度性质:如果将函数在时域上进行尺度变换,则其在频域上也会相应进行尺度变换。
具体而言,如果f(t)经过尺度变换得到ℎ(t)=f(at),那么它们的傅里叶变换满足H(ω)=1|a|F(ωa)。
常用函数的fourier变换傅里叶变换是以傅里叶级数为基础的,是一种对函数进行频域处理的技术。
它将函数在时域中的表示转换为在复平面上的表示,使得函数能够被分解成一些简单的正弦和余弦波。
在数学、物理学、工程学等领域,傅里叶变换被广泛应用于信号分析、图像处理、通信等方面。
常用函数是大量傅里叶变换的基础,下面将带领你分布说明常用函数的fourier变换。
1. 对于所有实数t,f(t)=1的傅里叶变换为F(ω)=2πδ(ω)其中,δ(ω)为狄拉克函数的傅里叶变换。
δ(ω)在原点处为1,在其它位置为0,在频域中作为单位冲击项。
2. 对于所有实数t,f(t)=2πδ(t)的傅里叶变换为F(ω)=1单位冲击项在时域中作为常数项,在频域中作为单位冲击项。
3. 对于所有实数t,f(t)=cos(ω0t)的傅里叶变换为F(ω)=π[δ(ω-ω0)+δ(ω+ω0)]cos(ω0t)在时域中作为周期为2π/ω0的函数,在频域中分解成两个单位冲击项,频率分别为±ω0。
4. 对于所有实数t,f(t)=sin(ω0t)的傅里叶变换为F(ω)=jπ[δ(ω-ω0)-δ(ω+ω0)]sin(ω0t)在时域中作为周期为2π/ω0的函数,在频域中分解成两个单位冲击项,频率分别为±ω0,其中一个带有负号。
5. 对于所有实数t,f(t)=e^jω0t的傅里叶变换为F(ω)=2πδ(ω-ω0)e^jω0t在时域中作为旋转相位的函数,在频域中作为单位冲击项。
6. 对于所有实数t,f(t)=u(t-a)的傅里叶变换为F(ω)=1/jωe^-jωau(t-a)在时域中作为比a大时为1,否则为0的函数,在频域中作为1/jωe^-jωa函数。
以上就是常见函数的fourier变换,通过这些例子,我们可以更好地理解傅里叶变换,以及在信号处理和图像处理等方面的应用。