§2-3 LTI系统的单位冲激响应

实验一 阶跃响应与冲激响应一、实验目的1、观察和测量RLC 串联电路的阶跃响应与冲激响应的波形和有关参数，并研究其电路元件参数变化对响应状态的影响；2、掌握有关信号时域的测量分析方法。

二、实验仪器1、信号源及频率计模块S2 1块2、模块一S5 1块3、数字万用表 1台4、双踪示波器 1台三、实验原理以单位冲激信号()t δ作为激励，LTI 连续系统产生的零状态响应称为单位冲激响应，简称冲激响应，记为()h t 。

冲激响应示意图如图2-1：图2-1冲激响应示意图以单位阶跃信号()u t 作为激励，LTI 连续系统产生的零状态响应称为单位阶跃响应，简称阶跃响应，记为()g t 。

阶跃响应示意图如图2-2：tt)(t u )(tg图2-2阶跃响应示意图阶跃激励与阶跃响应的关系简单地表示为：t)(t δ)(t h[])()(t u H t g = 或者 )()(t g t u →如图2-3所示为RLC 串联电路的阶跃响应与冲激响应实验电路图，其响应有以下三种状态：1、当电阻R ＞2 LC时，称过阻尼状态； 2、当电阻R = 2 LC时，称临界状态； 3、当电阻R ＜2LC时，称欠阻尼状态。

图2-3(a) 阶跃响应电路连接示意图图2-3(b) 冲激响应电路连接示意图冲激信号是阶跃信号的导数，即⎰-=td h t g 0ττ)()(，所以对线性时不变电路冲激响应也是阶跃响应的导数。

为了便于用示波器观察响应波形，实验中用周期方波代替阶跃信号。

而用周期方波通过微分电路后得到的尖顶脉冲代替冲激信号。

四、实验内容1、阶跃响应实验波形观察与参数测量 设激励信号为方波，频率为500Hz 。

实验电路连接图如图2-3（a ）所示。

① 调整激励信号源为方波（即从S2模块中的P2端口引出方波信号）；调节频率调节旋钮ROL1，使频率计示数f=500Hz 。

②连接S2模块的方波信号输出端P2至S5模块中的P12。

③示波器CH1接于TP14，调整W1，使电路分别工作于欠阻尼、临界和过阻尼三种状态，观察各种状态下的输出波形，用万用表测量与波形对应的P12和P13两点间的电阻值（测量时应断开电源），并将实验数据填入表格2-1中。

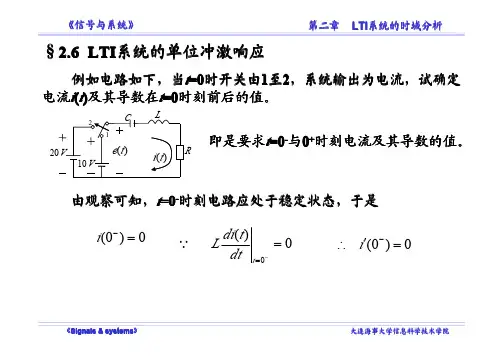
第一章1.8 系统的数学模型如下，试判断其线性、时不变性和因果性。

其中()0X -为系统的初始状态。

（2）()()2f t y t e= （5）()()cos 2y t f t t = （8）()()2y t f t =解：（2）()()2f t y t e =① 线性： 设 ()()()()1122,f t y t f t y t →→，则 ()()()()122212,f t f t y t ey t e==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t eee +⎡⎤⎣⎦+→==，显然，()()()1122y t a y t a y t ≠+，所以系统是非线性的。

② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f ty t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-，所以系统是时不变的。

③ 因果性因为对任意时刻 1t ，()()121f ty t e =，即输出由当前时刻的输入决定，所以系统是因果的。

（5）()()cos 2y t f t t = ① 线性： 设 ()()()()1122,f t y t f t y t →→，则 ()()()()1122cos 2,cos 2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+，所以系统是线性的。

② 时不变性设()()11,f t y t →则 ()()()()()1110100cos 2,cos 2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos 2y t f t t t y t t =-≠-，所以系统是时变的。

1． 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =，则该系统为 线性、时不变、因果。

（是否线性、时不变、因果？） 2． 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。

3． 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿.4． 若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5． 信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。

6． 系统阶跃响应的上升时间和系统的 截止频率 成反比。

7． 若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8． 为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的 左半平面 .9． 已知信号的频谱函数是））00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。

10． 若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1。

单位冲激函数总是满足)()(t t -=δδ （ √ ） 2。

满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。

( × ） 3.非周期信号的脉冲宽度越小,其频带宽度越宽。

( √ ）4。

连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

( √ ）5。

所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的. （ × ）三、计算分析题(1、3、4、5题每题10分,2题5分， 6题15分，共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

（完整）信号与系统专题练习题及答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）信号与系统专题练习题及答案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）信号与系统专题练习题及答案的全部内容。

信号与系统专题练习题一、选择题1．设当t<3时，x （t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。

A t>-2或t 〉-1B t=1和t=2C t>—1D t>—22．设当t<3时，x(t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。

A t 〉2或t>—1B t=1和t=2C t>-1D t 〉-23．设当t 〈3时，x （t ）=0，则使x(t/3）=0的t 值为 C 。

A t>3B t=0C t 〈9D t=34．信号)3/4cos(3)(π+=t t x 的周期是 C .A π2 B π C 2/π D π/25．下列各表达式中正确的是 BA 。

)()2(t t δδ= B. )(21)2(t t δδ= C 。

)(2)2(t t δδ= D. )2(21)(2t t δδ= 6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B 。

A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统7。

已知 系统的激励e （t)与响应r(t ）的关系为：)()(2t e t r = 则该系统为 C 。

A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。

实验三系统的冲激响应和阶跃响应分析一、实验目的掌握系统的冲激响应和阶跃响应的概念及其时域求解方法二、原理说明在L TI系统的时域分析中，除了可以利用经典方法求解某些系统的零状态响应外，还可以利用卷积积分求解系统的零状态响应。

这就需要求解系统的单位冲激响应和单位阶跃响应。

单位冲激响应h(t) 定义为系统初始状态为零，系统在冲激函数δ(t)作用下所产生的零状态响应.即h(t)=T[{0},δ(t)]其中T 为系统的变换算子。

而系统在任意激励f(t)作用下所形成的零状态响应Yf(t)=f(t)*h(t).单位冲激响应不仅在此有重要意义，而且对于描述系统的时域特性也有非常重要的意义。

单位阶跃响应g(t)定义为系统初始状态为零且在单位阶跃信号ε(t)作用下产生的零状态响应，即g(t)═ T[{0},ε(t)]。

二阶系统是工程中最常见的系统,在不同阻尼比ξ下，系统的阶跃响应不同。

三、预习要求单位冲激响应及阶跃响应的经典求解方法四、内容和步骤1. 二阶系统的传递函数为：2222)(nn n s s s H ωξωω++= 可用如下程序作出其单位阶跃响应和冲激响应波形曲线.(简单起见令n ω=1).参考程序一、CloseHold onzeta=[0.1 0.2 0.4 0.7 1.0];num=[1];t=0:0.01:12;for k=1:5den1=[1 2*zeta(k) 1];printsys (num,den1,’s’);[y1(:,k),x]=step(num,den1,t);den2=[1 zeta(k) 1];[y2(:,k),x]=impulse(num,den2,t);subplot(2,1,1),plot(t,y1(:,k));hold onsubplot(2,1,2),plot(t,y2(:,k));hold onend2. 自己构造一四阶以上连续系统系统函数,并求其阶跃响应和冲激响应波形.五、报告要求1.调试四1中程序,记录运行结果.2.用解析法求解步骤四1中系统的冲激响应和阶跃响应.3.若步骤四1中给定系统增加一个0 s处零点，系统时域特性有什么变化？4.写出步骤四1程序中各主要部分的功能5.分析系统时域响应波形，得出系统时域参数（上升时间和误差）永磁交流伺服电机位置反馈传感器检测相位与电机磁极相位的对齐方式2008-11-07 来源：internet 浏览：504主流的伺服电机位置反馈元件包括增量式编码器，绝对式编码器，正余弦编码器，旋转变压器等。

信号的时域运算及系统冲激响应一、实验目的1、掌握信号的基本时域变换和时域运算；2、用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号；3、牢固掌握系统的单位冲激响应的概念，掌握LTI系统的卷积表达式及其物理意义，掌握卷积的计算方法、卷积的基本性质；4、掌握利用MA TLAB计算卷积的编程方法，并利用所编写的MA TLAB程序验证卷积的常用基本性质；基本要求：掌握用MA TLAB实现各种信号的时域变换和运算，并且以图形的方式再现各种信号的波形。

掌握线性时不变连续系统的时域数学模型用MATLAB描述的方法，掌握卷积运算、线性常系数微分方程的求解编程。

二、实验原理1. 信号的时域变换与时域运算1.1 信号的时移信号的时移可用下面的数学表达式来描述：设一个连续时间信号为x(t)，它的时移y(t) 表示为：y(t) = x(t - t0)其中，t0为位移量。

若t0为正数，则y(t)等于将x(t)右移t0秒之后的结果。

反之，若t0为负数，则y(t)等于将x(t)左移t0秒之后的结果。

在MA TLAB中，时移运算与数学上习惯表达方法完全相同。

程序Program 1_5对给定一个连续时间信号x(t) = e-0.5t u(t)，对它分别左移2秒钟和右移2秒钟得到信号x1(t) = e-0.5(t+2)u(t+2)和x2(t) = e-0.5(t-2)u(t-2)。

% Program1_5% This program is used to implement the time-shift operation% on a continuous-time signal and to obtain its time-shifted versions% and to draw their plots.clear,close all,t = -5:0.01:5;x = exp(-0.5*t).*u(t); % Generate the original signal x(t)x1 = exp(-0.5*(t+2)).*u(t+2); % Shift x(t) to the left by 2 second to get x1(t)x2 = exp(-0.5*(t-2)).*u(t-2); % Shift x(t) to the right by 2 second to get x2(t)subplot(31 1)plot(t,x) % Plot x(t)grid on,title ('Original signal x(t)')subplot (312)plot (t,x1) % Plot x1(t)grid on,title ('Left shifted version of x(t)')subplot (313)plot (t,x2) % Plot x2(t)grid on,title ('Right shifted version of x(t)')xlabel ('Time t (sec)')1.2 信号的时域反褶对一个信号x[n]的反褶运算在数学上表示为y[n] = x[-n]这种反褶运算，用MATLAB实现起来也是非常简单的。