阶跃响应与冲激响应1

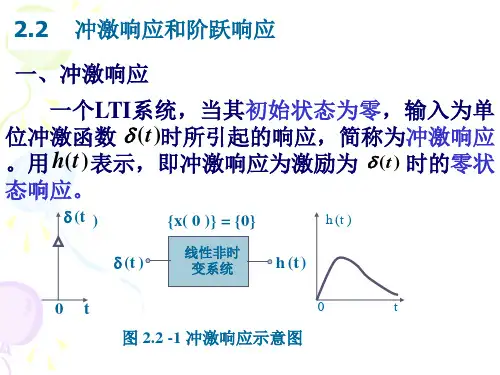
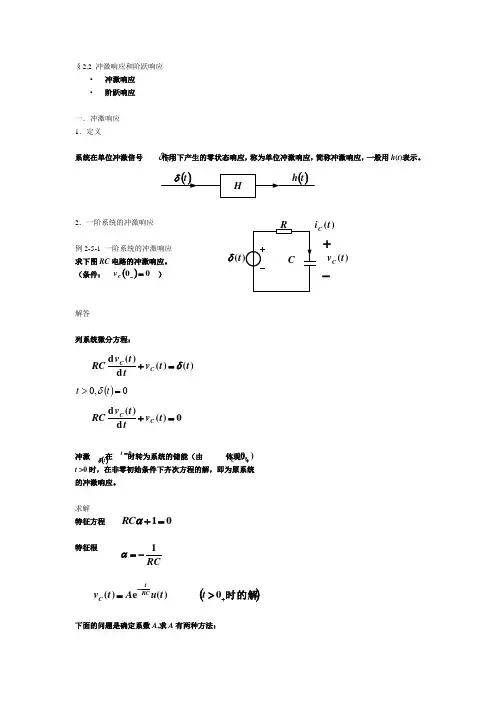
阶跃响应和冲激响应之间的关系阶跃响应和冲激响应是信号处理中常用的概念，它们之间存在着密切的关系。

阶跃响应描述了系统对于单位阶跃信号的输出响应，而冲激响应则描述了系统对于单位冲激信号的输出响应。

本文将从阶跃响应和冲激响应的定义、性质以及它们之间的关系进行详细介绍。

我们来看一下阶跃响应的定义。

阶跃响应是指系统对于单位阶跃信号的输出响应。

单位阶跃信号是一种在时间t=0时从0跳变到1的信号，它在t>0时始终保持为1。

阶跃响应描述了系统对于这种信号的输出情况。

接下来，我们来看一下冲激响应的定义。

冲激响应是指系统对于单位冲激信号的输出响应。

单位冲激信号是一种在时间t=0时瞬时出现，幅度为无穷大的信号，持续时间极短，但面积为1。

冲激响应描述了系统对于这种信号的输出情况。

阶跃响应和冲激响应之间存在着紧密的联系。

事实上，在很多情况下，我们可以通过冲激响应来求得阶跃响应。

这是因为单位阶跃信号可以看作是单位冲激信号的积分。

具体来说，我们可以将单位阶跃信号表示为单位冲激信号的积分形式。

假设单位阶跃信号为u(t)，单位冲激信号为δ(t)，那么单位阶跃信号可以表示为u(t)=∫δ(τ)dτ。

根据线性系统的性质，系统对于单位阶跃信号的输出可以表示为系统对于单位冲激信号的输出的积分形式。

换句话说，我们可以通过对系统的冲激响应进行积分，得到系统的阶跃响应。

这是因为阶跃信号是冲激信号的积分，而系统对于冲激信号的输出又可以通过冲激响应来描述。

阶跃响应和冲激响应之间的关系还可以通过频域的方法来理解。

在频域中，系统的阶跃响应和冲激响应之间存在着简单的关系。

阶跃响应可以通过冲激响应进行傅里叶变换得到，而冲激响应可以通过阶跃响应进行傅里叶变换得到。

总结起来，阶跃响应和冲激响应之间存在着密切的关系。

阶跃响应描述了系统对于单位阶跃信号的输出响应，而冲激响应描述了系统对于单位冲激信号的输出响应。

通过对冲激响应进行积分可以得到阶跃响应，而通过对阶跃响应进行傅里叶变换可以得到冲激响应。

实验1 阶跃响应与冲激响应一、实验目的1.观察和测量RLC串联电路的阶跃响应与冲激响应的波形和有关参数，并研究其电路元件参数变化对响应状态的影响；2.掌握有关信号时域的测量方法。

二、几个概念与解释1、系统的定义：系统是由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

从数学角度，也可理解为：系统也可定义为实现某种功能的运算。

2、响应：将输入信号（又称激励）作用于系统，得到的输出信号就称为响应。

3、零输入响应：没有外加激励信号的作用，只是由初始状态（初始时刻系统的储能）所产生的响应。

4、零状态响应：不考虑初始状态系统的储能作用（初始状态为零）由系统的外部激励信号所产生的作用。

5、冲激响应：将冲激信号作用于系统得到的输出信号就叫冲激响应。

6、阶跃响应：将阶跃信号作用于系统得到的输出信号就叫阶跃响应。

7、单位冲激响应：单位冲激信号作为激励，在系统中产生的零状态响应，就称为单位冲激响应。

8、单位阶跃响应：单位阶跃信号作为激励，在系统中产生的零状态响应，称为单位阶跃响应。

四、实验原理说明实验如图1-1所示为RLC 串联电路的阶跃响应与冲激响应的电路连接图图1-1（a ）为阶跃响应电路连接示意图图1-1（b ）为冲激响应电路连接示意图图1-1 (a) 阶跃响应电路连接示意图图1-1 (b) 冲激响应电路连接示意图其响应有以下三种状态：（1） 当电阻R ＞2 L C 时，称过阻尼状态；（2） 当电阻R = 2 L C时，称临界状态； （3） 当电阻R ＜2 L C 时，称欠阻尼状态。

以上两个电路的输出信号可以工作在：欠阻尼、临界和过阻尼三种状态下，可根据不同的需要进行选择。

根据电路中的参数计算出临界状态状态下的电阻值为R = 2 L C当：R =630.5Ω时，输出处于临界状态。

冲激信号是阶跃信号的导数，所以对线性时不变电路冲激响应也是阶跃响应的导数。

为了便于用示波器观察响应波形，实验用中用周期方波代替阶跃信号。

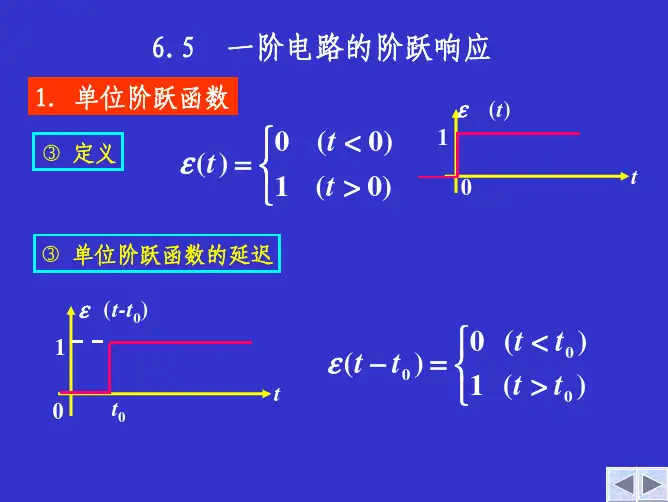
冲激响应和阶跃响应的关系冲激响应和阶跃响应是信号处理中常用的两种响应方式。

它们在时域和频域的特性不同，但在某些情况下存在一定的联系和关系。

冲激响应是指当输入信号为冲激函数（即单位脉冲函数）时，系统的输出响应。

冲激响应可以用于分析系统的频率响应特性，例如计算系统的频率响应函数、幅频特性和相频特性等。

冲激响应通常被表示为系统的单位脉冲响应函数。

阶跃响应是指当输入信号为阶跃函数（即单位阶跃函数）时，系统的输出响应。

阶跃响应可以用于分析系统的时域特性，例如计算系统的单位阶跃响应函数、过渡时间、稳态误差和阶跃响应曲线等。

阶跃响应通常被表示为系统的单位阶跃响应函数。

冲激响应和阶跃响应之间的关系可以通过拉普拉斯变换进行推导。

拉普拉斯变换是一种常用的信号处理工具，可以将时域的信号转换为复频域的函数。

通过拉普拉斯变换，我们可以将冲激响应和阶跃响应之间建立起联系。

对于一个线性时不变系统，假设其冲激响应为h(t)，阶跃响应为s(t)。

根据定义，阶跃响应可以表示为冲激响应的积分。

具体地，s(t)等于h(t)的积分，即s(t) = ∫h(τ)dτ，其中积分的上限是从0到t。

通过拉普拉斯变换，我们可以将上述关系表示为复频域的函数。

假设冲激响应的拉普拉斯变换为H(s)，阶跃响应的拉普拉斯变换为S(s)。

根据拉普拉斯变换的性质，阶跃响应的拉普拉斯变换可以表示为冲激响应的拉普拉斯变换除以s，即S(s) = H(s)/s。

从上述关系可以看出，冲激响应和阶跃响应之间存在一定的联系。

阶跃响应可以通过冲激响应的积分得到，而冲激响应可以通过阶跃响应的导数得到。

它们之间的关系可以帮助我们在信号处理中进行相互转换和分析。

除此之外，冲激响应和阶跃响应还可以用于系统的稳定性分析和系统参数估计。

通过对冲激响应和阶跃响应的分析，我们可以了解系统对不同类型输入信号的响应情况，进而判断系统的稳定性和性能。

冲激响应和阶跃响应在信号处理中扮演着重要的角色。

它们具有不同的时域和频域特性，但又存在一定的联系和关系。

单位阶跃响应和单位冲激响应关系嗨，亲们！今天我们来聊聊一个非常有趣的话题——单位阶跃响应和单位冲激响应关系。

让我们来简单了解一下这两个概念。

啥是单位阶跃响应呢？其实就是当我们把一个信号从0突然变成1的时候，系统会产生一种响应。

这种响应就是单位阶跃响应。

而单位冲激响应呢？其实就是当我们把一个信号从0突然变成1的时候，系统会产生一种响应。

这种响应就是单位冲激响应。

那么，这两个响应之间有什么关系呢？别着急，我们慢慢来分析。

我们来看一下单位阶跃响应。

当我们把一个信号从0突然变成1的时候，系统会产生一种响应。

这种响应可以用一个函数来表示，叫做单位阶跃函数。

这个函数的形状就像一个上坡的斜坡，开始的时候比较陡峭，后来就变得平缓了。

接下来，我们再来看一下单位冲激响应。

当我们把一个信号从0突然变成1的时候，系统同样会产生一种响应。

这种响应也可以用一个函数来表示，叫做单位冲激函数。

这个函数的形状就像一个上坡的斜坡，只不过它是直线上升的。

那么，这两个响应之间的关系究竟是什么呢？其实很简单，它们都是描述系统对输入信号的变化的反应。

只不过单位阶跃函数描述的是当输入信号从0突然变成1时的反应，而单位冲激函数描述的是当输入信号从0突然变成1时的反应。

所以说，这两个响应之间的关系就像是一对双胞胎兄弟，虽然长相有点儿像，但是性格却有很大的不同。

好了，现在我们已经知道了单位阶跃响应和单位冲激响应之间的关系。

那么，它们在实际应用中又是如何发挥作用的呢？其实很多哦！比如说，我们在设计控制系统的时候，就需要用到这两个函数来描述系统的性能；又比如说，我们在学习电路原理的时候，也需要用到这两个函数来帮助我们理解电路的工作过程。

单位阶跃响应和单位冲激响应之间的关系是非常重要的知识点。

希望大家在学习的过程中能够掌握它，并且能够在实际应用中发挥出它的价值。

好了，今天的分享就到这里啦！希望大家能够喜欢这篇文章，如果有什么问题或者建议，欢迎留言讨论哦！我们下期再见啦！。

系统的冲激响应和阶跃响应的关系(一)
系统的冲激响应和阶跃响应的关系
1. 冲激响应和阶跃响应的定义
•冲激响应是指系统在输入信号为单位冲激函数时的输出情况。

•阶跃响应是指系统在输入信号为单位阶跃函数时的输出情况。

2. 冲激响应和阶跃响应的关系
•冲激响应和阶跃响应之间存在一定的数学关系，即阶跃响应是冲激响应的积分。

•具体而言，阶跃响应是将冲激响应进行积分得到的，即用单位阶跃函数乘以冲激响应，再对得到的积分进行求解。

3. 冲激响应和阶跃响应关系的解释
•当输入信号为冲激函数时，系统对这个冲激函数进行处理后的输出即为冲激响应。

•而当输入信号为阶跃函数时，系统对这个阶跃函数进行处理后得到的输出即为阶跃响应。

•由于阶跃函数是冲激函数的积分形式，所以阶跃响应是冲激响应的积分形式。

4. 结论
•在不同的输入信号形式下，系统的输出表现也会有所不同。

•冲激响应描述了系统对冲激信号的处理情况，而阶跃响应则描述了系统对阶跃信号的处理情况。

•通过对冲激响应进行积分，可以得到对应的阶跃响应。

以上是关于系统的冲激响应和阶跃响应的关系的简要说明。

冲激响应和阶跃响应是信号处理中重要的概念，它们的关系可以帮助我们更好地理解和分析系统的输入输出特性。

信号与系统说明: 在时域，对于不同系统，零状态情况下加同样的激励如果冲激响应 不同，说明其系统特性不同， 冲激响应可以衡量系统的特性。

()t δ()h t 1．定义系统在单位冲激信号 作用下产生的零状态响应，称为单位冲激响应，简称冲激响应，一般用h (t )表示。

()t δ响应及其各阶导数(最高阶为n 次)2.冲激响应的数学模型1011110111d ()d ()d ()()d d d d ()d ()d ()()d d d n n n n n n m m m m m m r t r t r t C C C C r t t t te t e t e t E E E E e t t t t------++++=++++对于线性时不变系统,可以用一高阶微分方程表示()(1)(1)011()(1)(1)011()()()()()()()()n n n n m m m m C h t C h t C h t C h t E t E t E t E t δδδδ----++++=++++激励及其各阶导数(最高阶为m 次)令 e (t )=δ(t ) 则 r (t )=h (t )设特征根为简单根（无重根的单根）1()e ()()i nt i i h t A u t f t λ=⎛⎫=+ ⎪⎝⎭∑ 由于δ(t ) 及其导数在 t > 0+ 时都为零，因而方程式右端的自由项恒等于零，这样原系统的冲激响应形式与齐次解的形式相同。

②与n, m 相对大小有关①与特征根有关3. h (t ) 解的形式4.求法:直接代入确定待定系数()()n m h t t δ>不包含 及其各阶导数。

1()e ()i nt i i h t A u t λ=⎛⎫= ⎪⎝⎭∑()()n mh t t δ=包含 。

01()e ()()int i i h t C u t D t λδ=⎛⎫=+ ⎪⎝⎭∑()()n mh t t δ<包含 及其各阶导数，最阶次为m - n()∑∑-==+⎪⎭⎫ ⎝⎛=nm k k k n i t i t D t u C t h i 01)()(e )(δλ例: 系统微分方程为)(2d )(d )(3d )(d 4d )(d 22t e tt e t r t t r t t r +=++试求其冲激响应。

实验一阶跃响应与冲激响应一、试验目的1、观察和测量RLC串联电路的阶跃响应与冲激响应的波形和有关参数，并研究其电路元件参数变化对响应状态的影响。

2、熟悉掌握有关信号时域的测量方法。

二、试验设备双踪示波器（1台）信号系统实验箱（1台）三、实验原理阶跃响应与冲击响应有以下三种状态：1、当电阻R>2CL/时，称欠阻尼状态2、当电阻R=2CL/时，称临界阻尼状态3、当电阻R<2CL/时，称过阻尼状态冲击信号是阶跃信号的导数，所以对线性时不变电路冲击响应也是阶跃信号响应的导数。

四、实验内容及步骤1、阶跃响应波形观察与参数测量：设激励信号为方波，其幅度为4Vp-p,频率为1KHZ，即1ms。

（1）将函数信号源的频率调为1KHZ，幅度为4Vp-p,接近与TP103。

（2）示波器接近于TP104。

（3）调整R使其工作在三种状态。

2、冲激信号的产生是由阶跃信号经过微分电路得到。

实验电路如图1-1所示。

（1）将函数信号源接于TP101。

（频率与幅度不变）；（2）示波器接于TP102，观察经微分后响应的波形（等效为冲激激励信号）（3）连接TP102与TP103。

（4）示波器接于TP104（5）观察TP104端三种状态波形。

五、实验数据与数据处理1、阶跃响应波形（1）欠阻尼状态（2）临界阻尼状态(3) 过阻尼状态2、冲激响应（1）欠阻尼状态（2）临界阻尼状态（3）过阻尼状态六、实验心得从该实验中，让我懂得了示波器的用法，把理论与实践结合起来，更加熟悉掌握有关信号时域的测量方法。