(完整word版)北科大有限元资料2(判断题,课后思考题,知识点总结)
- 格式:doc
- 大小:54.50 KB
- 文档页数:9

有限元课后习题答案1.1有限元法的基本思想和基本步骤是什么首先,将表示结构的连续离散为若干个子域,单元之间通过其边界上的节点连接成组合体。
其次,用每个单元内所假设的近似函数分片地表示求解域内待求的未知厂变量。
步骤:结构的离散化,单元分析,单元集成,引入约束条件,求解线性方程组,得出节点位移。
1.2有限元法有哪些优点和缺点优点:有限元法可以模拟各种几何形状复杂的结构,得出其近似解;通过计算机程序,可以广泛地应用于各种场合;可以从其他CAD软件中导入建好的模型;数学处理比较方便,对复杂形状的结构也能适用;有限元法和优化设计方法相结合,以便发挥各自的优点。
缺点:有限元计算,尤其是复杂问题的分析计算,所耗费的计算时间、内存和磁盘空间等计算资源是相当惊人的。
对无限求解域问题没有较好的处理办法。
1.3有限元法在机械工程中有哪些具体的应用静力学分析模态分析动力学分析热应力分析其他分析2.1杆件结构划分单元的原则是什么?1)杆件的交点一定要取为节点2)阶梯形杆截面变化处一定要取为节点3)支撑点和自由端要取为节点4)集中载荷作用处要取为节点5)欲求位移的点要取为节点6)单元长度不要相差太多2.2简述单元刚度矩阵的性质。
单元刚度矩阵是描述单元节点力与节点位移之间关系的矩阵。
2.3有限元法基本方程中每一项的意义是什么?{Q}---整个结构的节点载荷列阵(包括外载荷、约束力);{}---整个结构的节点位移列阵;[K]---结构的整体刚度矩阵,又称总刚度矩阵。
2.4简述整体刚度矩阵的性质和特点。
对称性奇异性稀疏性主对角上的元素恒为正2.5位移边界条件和载荷边界条件的意义是什么由于刚度矩阵的线性相关性不能得到解,从而引入边界条件。
2.6写出平面刚架问题中单元刚度矩阵的坐标变换式2.7推导平面刚架局部坐标系下的单元刚度矩阵。
2.8简述整体坐标的概念。
单元刚度矩阵的坐标变换式把平面刚架的所有单元在局部坐标系X’O’Y’下的单元刚度矩阵变换到一个统一的坐标系xOy下,这个统一的坐标系xOy称为整体坐标系。



工程力学课后习题答案北科工程力学是一门应用力学原理研究工程结构和机械设备的学科,它是工程学的基础课程之一。
学习工程力学的过程中,课后习题是非常重要的一部分,通过解答习题可以巩固所学的知识,提高解决实际问题的能力。
在北科大学习工程力学的学生,经常会遇到一些难题,下面我将给出一些常见习题的答案和解析。
第一题:一根长为L的均匀杆AB,质量为m,放在光滑的水平桌面上,杆的一端A固定,另一端B由静止被释放。
当杆与桌面的夹角为θ时,求杆的加速度。
解析:根据牛顿第二定律,我们可以得到杆的受力分析图。
杆受到重力的作用,重力的分解力为mgcosθ和mgsinθ,其中mgcosθ垂直于桌面,不会对杆的运动产生影响,只有mgsinθ会使杆产生加速度。
由于杆是刚体,所以杆上各点的加速度大小相等,方向相同。
根据杆的运动学关系,我们可以得到加速度a=gsinθ。
第二题:一辆质量为m的小汽车以速度v通过一个半径为R的水平圆形弯道,小汽车受到向心力的作用,求小汽车通过弯道的最大速度。
解析:小汽车通过弯道时,受到向心力Fc的作用,向心力的大小为Fc=mv^2/R,向心力是由摩擦力提供的,所以摩擦力的大小也为Fc。
根据摩擦力的定义,摩擦力的大小为μN,其中μ为摩擦系数,N为小汽车受到的垂直于弯道的支持力。
由于小汽车在弯道上没有垂直于弯道的加速度,所以N=mg。
将摩擦力和向心力相等,可以得到μmg=mv^2/R,解得v^2=μgR,所以小汽车通过弯道的最大速度为v=√(μgR)。
第三题:一个质量为m的物体以速度v水平地撞击一个质量为M的静止物体,碰撞后两个物体一起运动,求碰撞后的速度。
解析:根据动量守恒定律,碰撞前后物体的总动量保持不变。
碰撞前物体的动量为mv,碰撞后物体的总动量为(m+M)V,其中V为碰撞后的速度。
所以可以得到mv=(m+M)V,解得V=mv/(m+M)。
以上是一些常见的工程力学课后习题的答案和解析,希望对北科大学习工程力学的学生有所帮助。

第二章 习题参考答案2-1解:由解析法,23cos 80RX F X P P N θ==+=∑故: 161.2R F N ==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有故: 3R F KN ==方向沿OB 。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:联立上二式,解得:0.577AB F W =(拉力)1.155AC F W =(压力)(b ) 由平衡方程有:联立上二式,解得:1.064AB F W =(拉力)0.364AC F W =(压力)(c ) 由平衡方程有:联立上二式,解得:0.5AB F W =(拉力)0.866AC F W =(压力)(d ) 由平衡方程有:联立上二式,解得:0.577AB F W =(拉力)0.577AC F W =(拉力)2-4解:(a )受力分析如图所示:由0x =∑ cos 450RA F P =由0Y =∑ sin 450RA RB F F P +-=(b)解:受力分析如图所示:由联立上二式,得:2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN =(压力)5RB F KN =(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由0x =∑ cos 0AC r F F α-=由0Y =∑ sin 0AC N F F W α+-=2-7解:受力分析如图所示,取左半部分为研究对象由0x =∑ cos45cos450RA CB P F F --=联立后,解得: 0.707RA F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由0x =∑ cos60cos300AC AB F F W ⋅--=联立上二式,解得: 7.32AB F KN =-(受压)27.3AC F KN =(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由0x =∑ sin cos 0DB T W αα-=(2)取B 点列平衡方程由0Y =∑ sin cos 0BD T T αα'-=2-10解:取B 为研究对象:由0Y =∑ sin 0BC F P α-=取C 为研究对象:由0x =∑ cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BC BC F F '= 解得:取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CE CE F F '=故有:2-11解:取A 点平衡:联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:由对称性及 AD AD F F '=2-12解:整体受力交于O 点,列O 点平衡由 0x =∑cos cos300RA DC F F P α+-=联立上二式得: 2.92RA F KN =1.33DC F KN =(压力)列C 点平衡联立上二式得: 1.67AC F KN =(拉力)1.0BC F KN =-(压力)2-13解:(1)取DEH 部分,对H 点列平衡联立方程后解得: RD F(2)取ABCE 部分,对C 点列平衡且 RE RE F F '=联立上面各式得: RA F =(3)取BCE 部分。

肯定有bug。
仅供参考。
1401052200隐式方法与显式方法:==静态隐式方法:不适用于短时高速下的大变形。
基于虚功原理,一般需要迭代(除迭代法外还有直接法)。
可能遇到迭代过程不收敛,以及方程组病态无确定解的问题。
ANSYS默认使用的方法。
动态显式方法:可用于短时、高速下的大变形。
基于动力学方程,每步计算形成新的刚度矩阵,无需迭代,不存在收敛性问题。
LS-DYDA模块(ANSYS中也包含)默认使用。
如何判断有限元的分析结果是正确的?1.有限元分析的结果能否与模型简化后存在的解析解对应;2.有限点处的计算结果与实验结果吻合;3.结果收敛;4.与实际经验吻合;……【结合书上P168】力学应力、温度热学分析提倡使用对称性,但不是所有的情况都能使用对称性,比如结构件的振动。
有限元方法:求解偏微分方程,基础为加权残值法。
求解有限元方程本质为解线性方程组。
ADD:要求所ADD的为同一种材料。
低阶单元:只有角节点,没有边中点或面内点的单元。
(目前已不使用面内点)高阶单元:不但有角节点,还有边中点或面内点的单元。
静态小变形使用高阶单元。
动态大变形使用低阶单元。
连续介质单元:求解得到位移。
结构单元:求解得到位移和转角。
求解结果的位移精度大于应力精度。
网格类型:三角形,四边形;四面体(三棱锥),五面体(三棱柱),六面体。
根据自由度关系,单元节点间存在铰接(自由度不同)和刚接(自由度相同)的关系。
连续介质单元也有一维单元(如接触关系)。
工字钢既可以使用梁单元,也可以使用连续介质单元。
对于直接法的求解效率:带宽解法:ANSYS的默认求解法;尽量减小单元内节点号差值从而减小带宽。
波阵解法:ABAQUS的默认求解法;尽量减小绕一节点所连接的单元号的差值从而减小波阵宽。
节点编号,从角节点开始,逆时针。
==使用子结构,可减少对内存的占用,但会增加时间消耗。
连续介质单元剖分后,只在节点上存在关系,公共边上位移相同,不出现重叠或分离。

1、有限元是近似求解一般连续场问题的数值方法2、有限元法将连续的求解域离散为假设干个子域,得到有限个单元,单元和单元之间用节点连接3、直梁在外力的作用下,横截面的内力有剪力和弯矩两个.4、平面刚架结构在外力的作用下横截面上的内力有轴力、剪力、弯矩.5、进行直梁有限元分析,平面刚架单元上每个节点的节点位移为挠度和转角6、平面刚架有限元分析,节点位移有轴向位移、横向位移、转角 .7、在弹性和小变形下,节点力和节点位移关系是线性关系.8、弹性力学问题的方程个数有15个,未知量个数有15个.9、弹性力学平面问题方程个数有8,未知数8个.10、几何方程是研究应变和位移之间关系的方程11、物理方程是描述应力和应变关系的方程12、平衡方程反映了应力和体力之间关系的13、把经过物体内任意一点各个截面上的应力状况叫做一点的应力状态14、9形函数在单元上节点上的值 ,具有本点为_1_.它点为零的性质,并且在三角形单元的任一节点上,三个行函数之和为_1_15、形函数是三角形单元内部坐标的线性函数他反映了单元的位移状态16、在进行节点编号时,同一单元的相邻节点的号差尽量小.17、三角形单元的位移模式为_线性位移模式_-18、矩形单元的位移模式为双线性位移模式19、在选择多项式位移模式的阶次时,要求_所选的位移模式应该与局部坐标系的方位无关的性质为几何各向同性20、单元刚度矩阵描述了节点力和节点位移之间的关系21、矩形单元边界上位移是连续变化的1.诉述有限元法的定义答:有限元法是近似求解一般连续场问题的数值方法2.有限元法的根本思想是什么答:首先,将表示结构的连续离散为假设干个子域,单元之间通过其边界上的节点连接成组合体.其次,用每个单元内所假设的近似函数分片地表示求解域内待求的未知厂变量.3.有限元法的分类和根本步骤有哪些答:分类:位移法、力法、混合法;步骤:结构的离散化,单元分析,单元集成,引入约束条件,求解线性方程组,得出节点位移.4.有限元法有哪些优缺点答:优点:有限元法可以模拟各种几何形状复杂的结构,得出其近似解;通过计算机程序,可以广泛地应用于各种场合;可以从其他CAD软件中导入建好的模型;数学处理比较方便, 对复杂形状的结构也能适用;有限元法和优化设计方法相结合,以便发挥各自的优点.缺点:有限元计算,尤其是复杂问题的分析计算, 所消耗的计算时间、内存和磁盘空间等计算资源是相当惊人的. 对无限求解域问题没有较好的处理方法. 尽管现有的有限元软件多数使用了网络自适应技术, 但在具体应用时,采用什么类型的单元、多大的网络密度等都要完全依赖适用者的经验.5.梁单元和平面钢架结构单元的自由度由什么确定答:由每个节点位移分量的总和确定6.简述单元刚度矩阵的性质和矩阵元素的物理意义答:单元刚度矩阵是描述单元节点力和节点位移之间关系的矩阵单元刚度矩阵中元素aml的物理意义为单元第L个节点位移分量等于1,其他节点位移分量等于0时,对应的第m个节点力分量.7.有限元法根本方程中的每一项的意义是什么P14答:Q——整个结构的节点载荷列阵〔外载荷、约束力〕;整个结构的节点位移列阵;结构的整体刚度矩阵,又称总刚度矩阵.8.位移边界条件和载荷边界条件的意义是什么答:由于刚度矩阵的线性相关性不能得到解,引入边界条件,使整体刚度矩阵求的唯一解.9.简述整体刚度矩阵的性质和特点P14答:对称性;奇异性;稀疏性;对角线上的元素恒为正.10简述整体坐标的概念P25答:在整体结构上建立的坐标系叫做整体坐标,又叫做统一坐标系.11.简述平面钢架问题有限元法的根本过程答:1〕力学模型确实定,2〕结构的离散化,3〕计算载荷的等效节点力,4〕计算各单元的刚度矩阵,5〕组集整体刚度矩阵,6〕施加边界约束条件,7〕求解降价的有限元根本方程, 8〕求解单元应力,9〕计算结果的输出.12.弹性力学的根本假设是什么.答:连续性假定,弹性假定,均匀性和各向同性假定,小变形假定,无初应力假定.13.弹性力学和材料力学相比,其研究方法和对象有什么不同.答:研究对象:材料力学主要研究杆件,如柱体、梁和轴,在拉压、剪切、弯曲和扭转等作用下的应力、形变和位移.弹性力学研究各种形状的弹性体,除杆件外,还研究平面体、空间体,板和壳等.因此,弹性力学的研究对象要广泛得多.研究方法:弹性力学和材料力学既有相似之外,又有一定区别.弹性力学研究问题,在弹性体区域内必须严格考虑静力学、几何学和物理学三方面条件,在边界上严格考虑受力条件或约束条件,由此建立微分方程和边界条件进行求解,得出较精确的解答.而材料力学虽然也考虑这几方面的条件,但不是十分严格的,材料力学只研究和适用于杆件问题. 14.简述圣维南原理. 答;把物体一小局部上的面力变换为分布不同但静力等效的面力,但影响近处的应力分量, 而不影响远处的应力.“局部影响原理〞15.平面应力问题和平面应变问题的特点和区别各是什么试各举出一个典型平面应力和平面应变的问题的实例.答:平面应力问题的特点:长、宽尺寸远大于厚度,沿板面受有平行板的面力,且沿厚度均匀分布,体力平行于板面且不沿厚度变化,在平板的前后外表上无外力作用平面应变问题的特点:Z向尺寸远大于x、y向尺寸,且与z轴垂直的各个横截面尺寸都相同,受有平行于横截面且不沿z向变化的外载荷,约束条件沿z向也不变,即所有内在因素的外来作用都不沿长度变化.区别:平面应力问题中z方向上应力为零,平面应变问题中z方向上应变为零、应力不为零.举例:平面应力问题等厚度薄板状弹性体,受力方向沿板面方向,荷载不沿板的厚度方向变化,且板的外表无荷载作用.平面应变问题一一水坝用于很长的等截面四柱体,其上作用的载荷均平行于横截面,且沿柱长方向不变法.16.三角形常应变单元的特点是什么矩形单元的特点是什么写出它们的位移模式.答:三角形单元具有适应性强的优点,较容易进行网络划分和逼近边界形状,应用比较灵活.其缺点是它的位移模式是线性函数,单元应力和应变都是常数,精度不够理想.矩形单元的位移模式是双线性函数,单元的应力、应变式线性变化的,具有精度较高, 形状规整,便于实现计算机自动划分等优点,缺点是单元不能适应曲线边界和斜边界,也不能随意改变大小,适用性非常有限.17.写出单元刚度矩阵表达式、并说明单元刚度与哪些因素有关.答:单元刚度矩阵与节点力坐标变换矩阵,局部坐标系下的单元刚度矩阵,节点位移有关的坐标变换矩阵.18.如何由单元刚度矩阵组建整体刚度矩阵〔叠加法〕答:〔1〕把单元刚度矩阵扩展成单元奉献矩阵 ,把单元刚度矩阵中的子块按其在整体刚度矩阵中的位置排列, 空白处用零子块填充.〔2〕把单元的奉献矩阵的对应列的子块相叠加, 即可得出整体刚度矩阵 .19.整体刚度矩阵的性质.答:〔1〕整体刚度矩阵中每一列元素的物理意义为:欲使弹性体的某一节点沿坐标方形发生单位为移,而其他节点都保持为零的变形状态,在各节点上所需要施加的节点力;〔2〕整体刚度矩阵中的主对角元素总是正的;〔3〕整体刚度矩阵是一个对称阵;〔4〕整体刚度矩阵式一个呈带状分布的稀疏性矩阵.〔5〕整体刚度矩阵式一个奇异阵,在排除刚体位移后,他是正定阵.20.简述形函数的概念和性质.答:形函数的性质有:〔1〕形函数单元节点上的值,具有“本点为一、他点为零〞的性质;〔2〕在单元的任一节点上,三角函数之和等于1; 〔3〕三角形单元任一一条边上的形函数,仅与该端点节点坐标有关,而与另外一个节点坐标无关;〔4〕型函数的值在0〜1之间变换.21.结构的网格划分应注意哪些问题 .如何对其进行节点编号.才能使半带宽最小.P50, P8相邻节点的号差最小答:一般首选三角形单元或等参元.对平直边界可选用矩形单元,也可以同时选用两种或两种以上的单元.一般来说,集中力,集中力偶,分布在和强度的突变点,分布载荷与自由边界的分界点,支撑点都应该取为节点,相邻节点的号差尽可能最小才能使半带宽最小22.为了保证解答的收敛性,单元位数模式必须满足什么条件答:〔1〕位移模式必须包含单元刚体位移;〔2〕位移模式必须包含单元的常应变;〔3〕位移模式在单元内要连续,且唯一在相邻单元之间要协调.在有限单元法中,把能够满足条件1和条件2的单元称为完备单元,把满足条件3的单元叫做协调单元或保续单元.23有限元分析求得的位移解收敛于真实解得下界的条件.答:1.位移模式必须包含单元的刚体位移,2.位移模式必须包含单元的常应变,3.位移模式在单元内要连续,且位移在相邻单元之间要协调.24.简述等参数单元的概念.答:坐标变换中采用节点参数的个数等于位移模式中节点参数的个数,这种单元称为等参单元.25.有限元法中等参数单元的主要优点是什么答:1〕应用范围广.在平面或空间连续体,杆系结构和板壳问题中都可应用.2〕将不规那么的单元变化为规那么的单元后,易于构造位移模式.3〕在原结构中可以采用不规那么单元,易于适用边界的形状和改变单元的大小.4〕可以灵活的增减节点,容易构造各种过度单元.5〕推导过程具有通用性.一维,二维三维的推导过程根本相同.26.简述四节点四边形等参数单元的平面问题分析过程.答:〔1〕通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;〔2〕通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;〔3〕将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵〔4〕用虚功原理球的单元刚度矩阵,,最后用高斯积分法计算完成.27.为什么等参数单元要采用自然坐标来表示形函数为什么要引入雅可比矩阵答:简化计算得到形函数的偏导关系.28. ANSYS软件主要包括哪些局部各局部的作用是什么答:1.前处理模块:提供了一个强大的实体建模及网络划分工具,用户可以方便地构造有限元模型.2.分析计算模块:包括结构分析、流体力学分析、磁场分析、声场分析、压电分析以及多种物理场的耦合分析,可以模拟多种物理介质的相互作用,具有灵敏度分析及优化分析水平.3.后处理模块:可将计算后果以彩色等值线显示、梯度显示、矢量显示、粒子流迹显示、立体切片显示、透明及半透明显示等图形方式显示出来,也可将计算结果以图表、曲线形式显示出来或输出.29. ANSYS软件提供的分析类型有哪些答:结构静力分析、机构动力分析、结构非线性分析、动力学分析、热分析、流体力学分析、电磁场分析、声场分析、压电分析.30.简述ANSYS软件分析静力学问题的根本流程.答:1.前处理器:1〕定义单元类型,2〕定义实常数,3〕定义材料属性,4〕创立实体几何模型,5〕划分网络;2.求解器:1〕定义分析类型,2〕施加载荷和位移约束条件,3〕求解;三角形三节点单元的位移是连续的,应变和应力在单元内是常数,因而其相邻单元将具有不同的应力和应变,即在单元的公共边界上和应变的值将会有突变.矩形单元的边界上,位移是线性变化的,显然,在两个相邻矩形单元的公共边界上,其位移是连续的.节点的选用原那么:一般说,集中力、集中力偶、分布载荷强度的突变点、分布载荷与自由边界的分界点、支承点都能赢取为节点.单元的划分原那么:〔1〕划分单元的数目,视要求的计算精度和计算机的性能而定.〔2〕单元的大小,可根据部位的不同而有所不同.1、试述街节点力和节点载荷的区别.节点力是单元与节点之间的作用力;如果取整个结构为研究对象,节点力为内力,节点载荷是作用在节点上的外载荷.2、试述求整体刚度矩阵的两种方法.分别建立各节点的平衡方程式,写成矩阵形式,可求得整体刚度矩阵;将各单元刚度矩阵按规律叠加,也可得整体刚度矩阵.3、平面问题中划分单元的数目是否越多越好不是越多越好.划分单元的数目,视要求的计算精度和计算机的性能而定.随着单元数目的接连多,有限元解逐步逼近于真实解,但是,单元数目接连加,刚求解的有限元线性方程组的数目接连多, 需要占用更多的计算机内存资源,求解时间接连长,所以,在计算机上进行有限元分析时,还要考虑计算机的性能.单元数过多并不经济.4、写出单元刚度矩阵的表达式,并说明单元刚度与那些因素有关[B]-单元应变矩阵,[D]-弹性矩阵,t-厚度〕单元刚度矩阵取决于单元的大小、方向、和弹性常数,而与单元的位置无关,即不随单元或坐标轴的平移而改变.5、选择多项式为单元的位移模式时,除了要满足单元的完备性和协调性要求,还须考虑什么因素还须考虑两个因素:1、所选的位移模式应该与局部坐标系的方位无关,即几何各向同性. 2、多项式位移模式中的项数必须等于或稍大于单元边界上的外节点的自由度数,通常取多项式的项数与单元的外节点的自由度数想等.。
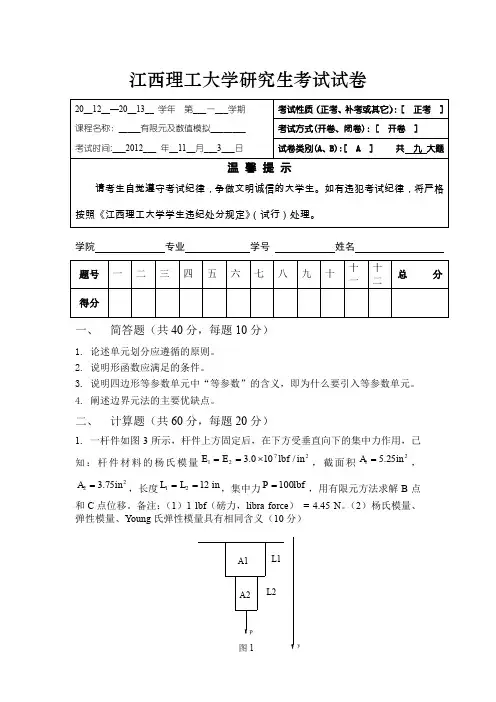
江西理工大学研究生考试试卷一、 简答题(共40分,每题10分)1. 论述单元划分应遵循的原则。
2. 说明形函数应满足的条件。
3. 说明四边形等参数单元中“等参数”的含义,即为什么要引入等参数单元。
4. 阐述边界元法的主要优缺点。
二、 计算题(共60分,每题20分)1. 一杆件如图3所示,杆件上方固定后,在下方受垂直向下的集中力作用,已知:杆件材料的杨氏模量2721/100.3in lbf E E ⨯==,截面积2125.5in A =,2275.3in A =,长度in L L 1221==,集中力lbf P 100=,用有限元方法求解B 点和C 点位移。
备注:(1)1 lbf (磅力,libra force ) = 4.45 N 。
(2)杨氏模量、弹性模量、Young 氏弹性模量具有相同含义(10分)20__12__—20__13__ 学年 第___一___学期 课程名称:_____有限元及数值模拟________ 考试时间:___2012___ 年__11__月___3___日考试性质(正考、补考或其它):[ 正考 ] 考试方式(开卷、闭卷):[ 开卷 ] 试卷类别(A 、B):[ A ] 共 九 大题温 馨 提 示请考生自觉遵守考试纪律,争做文明诚信的大学生。
如有违犯考试纪律,将严格按照《江西理工大学学生违纪处分规定》(试行)处理。
学院 专业 学号 姓名 题号 一二三四五六七八九十十一十二总 分得分pyA1A2L1L2图12. 如图2所示,有一正方形薄板,沿对角承受压力作用,厚度t=1m,载荷F=20KN/m,设泊松比µ=0,材料的弹性模量为E,试求它的应力分布。
(15分)图23. 图示结点三角形单元的124边作用有均布侧压力q,单元厚度为t,求单元的等效结点荷载。
图3一、简答题1. 答:1)合理安排单元网格的疏密分布2)为突出重要部位的单元二次划分3)划分单元的个数4)单元形状的合理性5)不同材料界面处及荷载突变点、支承点的单元划分6)曲线边界的处理,应尽可能减小几何误差7)充分利用结构及载荷的对称性,以减少计算量2. 答:形函数应满足的三个条件:a.必须能反映单元的刚体位移,就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。

2 弹性力学问题的有限单元法思考题2.1 有限元法离散结构时为什么要在应力变化复杂的地方采用较密网格,而在其他地方采用较稀疏网格?答:在应力变化复杂的地方每一结点与相邻结点的应力都变化较大,若网格划分较稀疏,则在应力突变处没有设置结点,而使得所求解的误差很大,若网格划分较密时,则应力变化复杂的地方可以设置更多的结点,从而使得所求解的精度更高一些。
2.2 因为应力边界条件就是边界上的平衡方程,所以引用虚功原理必然满足应力边界条件,对吗?答:对。
2.3 为什么有限元只能求解位移边值问题和混合边值问题?弹性力学中受内压和外压作用的圆环能用有限元方法求解吗?为什么?答:有限元法是一种位移解法,故只能求解位移边值问题和混合边值问题。
而应力边值问题没有确定的位移约束,不能用位移法求解,所以也不能用有限元法求解。
2.4 矩形单元旋转一个角度后还能够保持在单元边界上的位移协调吗?答:能。
矩形单元的插值函数满足单元内部和单元边界上的连续性要求,是一个协调元。
矩形的插值函数只与坐标差有关,旋转一个角度后各个结点的坐标差保持不变,所以插值函数保持不变。
因此矩形单元旋转一个角度后还能够保持在单元边界上的位移协调。
2.5 总体刚度矩阵呈带状分布,与哪些因素有关?如何计算半带宽? 答:因素:总体刚度矩阵呈带状分布与单元内最大结点号与最小结点号的差有关。
计算:设半带宽为B ,每个结点的自由度为n ,各单元中结点整体码的最大差值为D ,则B=n(D+1),在平面问题中n=2。
2.6 为什么单元尺寸不要相差太大,如果这样,会导致什么结果? 答:由于实际工程是一个二维或三维的连续体,将其分为具有简单而规则的几何单元,这样便于网格计算,还可以通过增加结点数提高单元精度。
在几何形状上等于或近似与原来形状,减小由于形状差异过大带来的误差。
若形状相差过大,使结构应力分析困难加大,误差同时也加大。
2.7 剖分网格时,在边界出现突变和有集中力作用的地方要设置结点或单元边界,试说明理由。

1.按照研究方法,分为:连续介质单元,(三角形,四边形)——弹性力学结构单元(四面体,五面体,六面体)——结构力学2.连续介质单元是否有一维单元?是!——边界层单元3.为什么商业软件中,节点是乱的?因为这是软件自动优化的结果,以便于优化带宽或者波宽;4.单元分析时如何编号?从某一个角节点开始,按照逆时针进行编号!5.形函数的性质有哪些?a)其中,意思是关于i节点的形函数取本节点值时,形函数值为1,关于i节点的形函数取其他节点值时,形函数值为0。
b)在单元内任一点,位移的插值之和可以归一,否则不能反映单元刚体位移。
c)对于三节点三角形单元,形函数为线性插值函数。
6.有限元可不可以无模型就有网格?可以。
7.ANSYS中什么叫P方法,什么叫h方法?H方法:指的是把网格加密使得单元特征尺寸变小,从而达到提高计算机计算进度的目的。
P方法:网格不变,提高差值函数的阶数,以提高计算精度的方法。
8.做流固分析最好的软件是什么?ANSYS9.特征值计算不允许使用对称性,如做热场分析的时候千万不能用对称性,否则就成了绝热了。
10.有关单元分类:一维单元:线单元(结构单元,如:杆单元,梁单元)、连续单元(接触线单元);二维单元:结构单元(壳单元)、连续单元(三单元、四单元。
注意没有五边形单元,只有三角形,四边形);三维单元:连续体单元(四面体-三棱锥、五面体-三棱柱、六面体)2D:四边形较好,3D:六面体较好,四面体精度较差,但是传热学就无所谓了11.当出现Copy命令的时候,注意事项:1)如果实体已经被划分网格,则网格同时被复制;2)如果新-旧网格具有共同边界,两网格之间并没有联系;3)可以在组坐标中进行拷贝,但是只允许环向角度(DY)增量复制以及Z芳香(DZ)增量复制。
12.Reflect命令:a)如果实体已经被划分网格,则经过镜像后,网格同时被复制。
b)如果新-旧网格具有共同边界,两网格之间并没有联系。
c)所有的方向均按激活坐标系,且必须是直角坐标系。
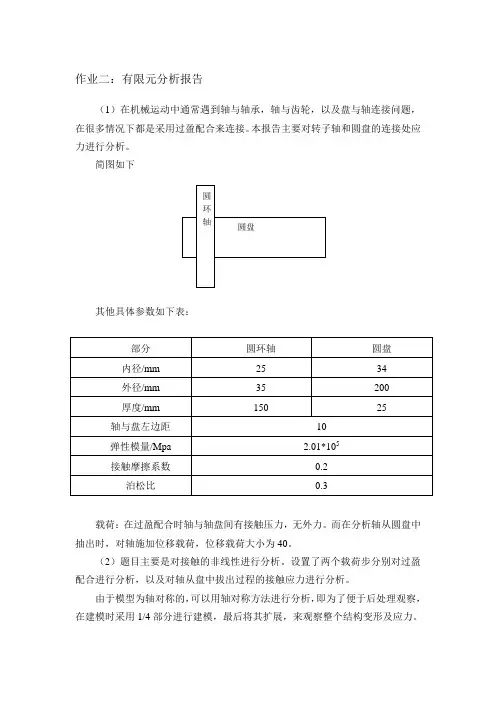
作业二:有限元分析报告(1)在机械运动中通常遇到轴与轴承,轴与齿轮,以及盘与轴连接问题,在很多情况下都是采用过盈配合来连接。
本报告主要对转子轴和圆盘的连接处应力进行分析。
简图如下其他具体参数如下表:部分 圆环轴 圆盘 内径/mm 25 34 外径/mm 35 200 厚度/mm 15025轴与盘左边距 10 弹性模量/Mpa 2.01*105 接触摩擦系数 0.2 泊松比0.3载荷:在过盈配合时轴与轴盘间有接触压力,无外力。
而在分析轴从圆盘中抽出时,对轴施加位移载荷,位移载荷大小为40。
(2)题目主要是对接触的非线性进行分析。
设置了两个载荷步分别对过盈配合进行分析,以及对轴从盘中拔出过程的接触应力进行分析。
由于模型为轴对称的,可以用轴对称方法进行分析,即为了便于后处理观察,在建模时采用1/4部分进行建模,最后将其扩展,来观察整个结构变形及应力。
圆盘圆环轴本题主要分析接触处应力,在建模时不考虑倒角与圆角,这样便于计算与划分网格。
(3)几何模型的建立。
考虑到模型为轴对称问题,在建模时不需要把整个模型都建立出来,只需要建立模型的1/4,在分析完后再映射为整个模型。
报告中模型数据已给出。
在ANSYS中通过前处理模块建模功能创建圆环实体。
利用Create-V olumes-Cylinder-Partial-Cylinder命令赋予圆盘与圆环轴的参数,先后创建圆盘与圆环轴。
进行等轴测显示Pan Zoom Rotate 中Iso,并将圆环轴移动,使其有正确位置(和圆盘Z方向有位移10)。
最终得到模型图如下。
(4)本题目选用的8节点单元,具体为Structural Solid-Brick 8 node185单元。
因为分析内容属于实体范畴,模型形状规则,简单,可以比较方便的划分为六面体单元,计算量小。
故优先选用8 node185。
(5)两接触固体均为规则的几何平面,进行网格划分时采用的线控方式。
对圆环轴以及圆盘分别对各边线进行等分,具体在size controls下Lines中Set 中进行设置。
广西科技大学硕士研究生课程考试参考答案及评分标准(学年第学期)考试科目:(A/B卷)考试班级:考试形式:(开/闭卷)考试时间:分钟考试人数:命题人签名:系分管领导签名:一.判断题(每小题2分,共20分)1.×2. √3. √4. ×5. √6. √7. √8. √9. √ 10. √二.选择题(每小题2分,共20分)1.D2.B3.A4.B5.A6.B7.C8.B9.C 10.B三.简答题(共3题,每小题5分)1.答:杆单元只能承受拉压荷载,梁单元则可以承受拉压弯扭荷载。
具体的说,杆单元其实就是理论力学常说的二力杆,它只能在结点受载荷,且只有结点上的荷载合力通过其轴线时,杆件才有可能平衡,像均布荷载、中部集中荷载等是无法承担的,通常用于网架、桁架的分析;而梁单元则基本上适用于各种情况(除了楼板之类),且经过适当的处理(如释放自由度、耦合等),梁单元也可以当作杆单元使用。
2.答:对称性,奇异性,主对角元恒正,稀疏性,非零元素呈带状分布。
3.答:1.建立求解域,并将之离散化成有限个单元,即将问题分解成节点和单元。
2.假定描述单元物理属性的形函数,即用一个近似的连续函数描述每个单元的解。
3.建立单元刚度矩阵。
4.组装单元,构造总刚矩阵。
5.应用边界条件和初值条件,并施加荷载。
6.求解线性或非线性微分方程得到节点值。
7.分析计算,进行后处理四.计算题(共2题,每小题22分)1.解:对各单元节点编号,各单元刚度矩阵为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1111121131211221231311321331k k k k k k k k k k []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2442432422342332322242232222k k k k k k k k k k (5分) []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3333343353433443453533543553k k k k k k k k k k []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=4664654644564554544464454444k k k k k k k k k k (5分) 组集各单元刚度矩阵,得到总体刚度矩阵:[][][][][][][][][][][][][][][][][][][][][][][][][]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+++++++++=466465464454354454354353444344244343243242333233133232132131222122121111k k k k k k k k k k k k k k k k k k k k k k k k k 对称 (5分)2.解:根据形函数性质:⎩⎨⎧≠==j i ji x x N j i i 01),( 对于结点1而言,),(1ηξN 在结点2、3、4处的值为0。
(完整版)北科大材料力学答案版.doc自觉遵装守订考试线规则内,诚不信考得试,答绝不题作弊北京科技大学 2012--2013 学年第 2 学期工程力学 AII 试卷( A )院 (系) 班级学号姓名试卷卷面成绩占课平时成绩课程考程考占核成绩题号一二三四五六小计核成20%得分得分一、判断题(20分,每题2分,将“√”或者“X”填入题后括号内。
)1. 材料力学主要研究强度、刚度和稳定性问题。
(√)2. 矩形截面梁由剪力引起的剪应力在中性层为0,上下边缘处最大。
( X )3. 结构刚度越大 ,变形越小 ,也越不容易失稳。
(√)4. 塑性材料和脆性材料的失效破坏机理是一样的。
( X )5. 单位载荷法等能量方法可以直接用于求梁结构中的最大应力。
( X )6. 电测法的基本原理是将结构变形引起电阻丝长度变化,进而导致电阻等电学物理量的变化 ,由电学量的变化反推可得到结构的变形信息。
(√)7. 低碳钢扭转破坏试验后其断口平面与轴线垂直。
(√)8.测低碳钢的弹性模量与泊松比时在其上下表面各贴一个应变片,其主要考虑是得到双倍的应变值 ,因为越大的物理量测量精度一般越高。
( X )9. 铸铁试件的拉伸和扭转失效 ,主要原因都是最大剪应力超过了许用值。
( X )10. 对于主要受挤压的结构件,允许结构中出现部分的塑性变形。
(√)得分二、如图所示外伸梁,B为固定铰,C为移动铰,A端受集中力P=10 kN,B点受一集中力偶 M=40 kNm,HD 段受均布力 q=10 kN/m ,AB 、 BH、HC 和 CD 各段的长度均为 L=1 m,试作出梁的弯矩图和剪力图。
(20 分)qMA BDHPN B和C解:解除 B 点和 C 点约束,分别代之以约束反力 CN ,由M B 0,即PL M 2qL 2L N C 2LN C M PL 4qL245 kN (2 分)2L由M C 0,即3PL M N B2LN B M 3PL(2 分)35 kN2L2 分,一共 16 分,加上支反力 4 分,共计 20 分。
材料力学期中测验
--杆件受力的有限元计算
问题 1 分布载荷作用下的悬臂梁应力计算
分析模型如图1-1 所示, 梁的横截面为矩形宽х高 = 1х 2 m2. 受到分布载荷作用。
材料的弹性模量200GPa, 泊松比0.3。
习题文件名: Cantilever beam。
注意:用实体单元离散,长度单位m, 力的单位 N,对应应力单位 Pa,按照平面应力处理。
问题2表面效应
单元模拟一螺栓扭转问题
问题描述:表面效应单元:类似一层皮肤,覆盖在实体单元的表面。
它利用实体表面的节点形成单元。
因此,表面效应单元不增加节点数量(孤立节点除外),只增加单元数量。
用ANSYS 对螺栓模型施加扭转荷载,求解并在后处理器中观察整体柱坐标系下的UY 。
载荷和边界条件:沿螺栓上端的扭矩Mt 等效为切向等效切应力:q=10MPa ,底部固定 (UX=UY=UZ=0)。
设:螺栓直径d=100mm ,螺栓长度L=200mm ,螺帽直径D=160mm,螺帽高度H=30mm 。
材料应力—应变关系为线弹性模型,弹性模量200E GPa =,泊松比3.0=ν。
问题 3 悬臂“工”字梁的屈曲建模计算计算模型如下图:
基本参数:集中力F=106N杨氏弹性模量E=2.0e5MPa,泊松比v=0.2,梁长度为2.5 m。
横截面积尺寸见下表:
梁的横截面积尺寸(单位:㎜)
宽度B 高度H 腹板厚t1 翼缘厚t2
150 250 15 15
L
F。
(完整word版)北师大版“中国古代文学史”课后思考题《中国古代文学史》课后思考题先秦文学思考题1.比较《诗经》中“国风”和“小雅”诗的风格特征.2.试述风、雅、颂的文体特征。
3.试述赋、比、兴的文学意义。
4.试析《诗经》怨刺诗的思想和表达特点。
5.论述《诗经》的现实精神。
6.试论《诗经》的基本情感特征.7.试论《诗经》的形式特征。
8.试论《诗经》对后世文学的影响。
9.简述《春秋》记事的特征。
10.古人是如何论述《春秋》的“微言大义”的?11.《左传》的理性精神是如何通过叙事表现出来的?12.论《左传》人物描写的特点。
13.试析《左传》战争描写的特点。
14.试析《左传》的叙事特征.15.试述《左传》的记言特征。
16.结合战国文化背景,论述《战国策》的思想特征.17.试述策士的基本游说技巧。
18.试述《战国策》寓言的特征。
19.比较《左传》和《战国策》说辞的艺术特征.20.从陈述方式、语体风格等方面比较“语录体”和“论辨体”散文的特征。
21.谈谈先秦议论散文的文体发展线索.22.举例说明《孟子》文章“循循善诱”的表达特征。
23.试析《庄子》的文体特征.24.论述《庄子》的艺术特征。
25.简析《庄子》文章中意象的特点。
26.简述《荀子》的文章体制的特点.27.从结构、意象、论述方式等方面谈谈《庄子》散文的“诗性”特征。
28.简述《韩非子》文章风格特征。
29.具体比较《孟子》、《庄子》、《韩非子》三书中寓言的不同特征。
30.简述《离骚》的主题思想。
31.试述《离骚》的艺术特色。
32.谈谈《离骚》和《九歌》在运用象征手法上的共同特点。
33.简述《九歌》表达相思之情的特点。
34.试论《天问》的结构特征。
35.简述宋玉的文学成就.36.简述屈原和楚辞对后世文学的影响。
两汉文学思考题1.汉代的经学对文学的发展产生了什么影响?2.汉代的文学思想有哪些主要观点?(完整word版)北师大版“中国古代文学史”课后思考题3.西汉前期的论说文有什么共同特点?从朝廷作家和藩国作家中各举一个例子加以说明.4.汉武帝时期的论说文出现了哪三种倾向?为什么会出现这些倾向?5.西汉后期和东汉时期儒道两家思想对论说文创作各有什么影响?6.贾谊、晁错等西汉散文家在哪些方面继承了战国说辞的艺术成就。
北京科技大学2009—2010学年硕士研究生“工程中的有限元方法”试题姓名__________________ 学号______________________班级______________ 成绩________________ 说明:1--5题为笔试题,每题10分。
上机题结合实验报告共50分。
1、 简述弹性力学四边形四节点等参元的收敛性质以及由该单元刚度矩阵装配成的总刚度矩阵的性质。
在单元分析已经提出有限单元解的收敛性要求, 即, 单元必须是完备的和协调的。
对于等参单元:1.完备性:对于C0型单元,由于等参单元的形函数中包含有常数项和线性项,满足完备性的要求。
2. 协调性:由于单元之间的公共边上有完全相同的节点, 同时每一单元沿这些边的坐标和未知函数均采用相同的插值函数加以确定。
因此, 只要在划分网格时, 遵守单元选择和节点配置的要求, 则等参单元满足协调性的要求。
2. 总刚的性质1)对称性2)奇异性,需引入合适的位移约束。
3)稀疏,(存在许多零元素)4)非零元素呈带状分布5)主元恒正根据物理意义可得此性质,正常情况下,主元占优2、 分析图示的两个单元在什么条件下其连接关系正确。
要求说明所采用单元的类型和连接方法。
采用四边形等参元附加多点约束方程过渡。
4边形5节点Serendipity 过渡单元 约束方程:u 6=(u 2+u 3)/23、对于右图所示三节点网格,设每个节点具有一个自由度。
其: 最大带宽= (9-1)*1=8 最大波阵宽=3 1,2,10 9,2,109,2,39,8,34,8,3.4、某非协调板单元,单元长度为2⨯2,节点基本未知量为: ()(),,,(1,2,3,4)T i i i i w w w i y x φ⎡⎤∂∂=-=⎢⎥∂∂⎣⎦ 在图示的坐标系下,其关于w 的插值函数形式为:其中:试:(1)说明此插值函数属于哪一族插值函数?(2)说明此插值函数具有什么基本性质?Hermite 族插值函数插值函数及其导函数均具有δij 的性质。
1、弹性力学和材料力学在研究对象上的区别?6答:材料力学的研究对象是杆状构件,即长度远大于宽度和厚度的构件。
弹性力学除了研究杆状构件外,还研究板、壳、块,甚至是三维物体等,弹性力学的研究对象要广泛得多。
2、理想弹性体的五点假设?答:连续性假定、完全弹性假定、均匀性假定、各向同性假定、小位移和小变形的假定。
3、什么叫轴对称问题,采用什么坐标系分析?为什么?答:如果弹性体的几何形状、约束状态以及外载荷都对称于某一根轴,那么弹性体所有的位移、应变和应力也都对称于这根轴,这类问题称为轴对称问题。
对于轴对称问题,采用圆柱坐标。
当以弹性体的对称轴为Z轴时,则所有的应力分量,应变分量和位移分量都只与坐标r、z有关,而与θ无关。
4、梁单元和杆单元的区别?答:主要区别是受力不同,梁单元主要承受弯矩,杆单元主要承受轴向力。
杆单元通常用于网架、桁架的分析;而梁单元则基本上可以适用于各种情况。
5、薄板弯曲问题与平面应力问题的区别?答:平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板,但前者受力特点是平行于板面且沿厚度均布载荷,变形发生在板面内;后者受力特点是当承受垂直于板面的载荷时,板在弯曲应力和扭转应力作用下将变成曲面板。
6、有限单元法结构刚度矩阵的特点?答:主对称元素总是正的;对称性;稀疏性;奇异性;非零元素呈带状分布。
7、有限单元法的收敛性准则?答:完备性要求,协调性要求。
完备性要求。
如果出现在泛函中场函数的最高阶导数是m阶,则有限元解收敛的条件之一是单元内场函数的试探函数至少是m次完全多项式。
或者说试探函数中必须包括本身和直至m 阶导数为常数的项。
单元的插值函数满足上述要求时,我们称单元是完备的。
协调性要求。
如果出现在泛函中的最高阶导数是m阶,则试探函数在单元交界面上必须具有Cm-1连续性,即在相邻单元的交界面上应有函数直至m-1阶的连续导数。
当单元的插值函数满足上述要求时,我们称单元是协调的。
8、简述圣维南原理在工程实际中的应用?答:物体小部分边界上的面力是平衡力系,则近处产生显著应力,远处应力小到忽略不计。
在工程实际中物体所受的外载荷往往比较复杂,一般很难完全满足边界条件。
当所关心的并不是载荷作用区域内的局部应力分布时,可以利用圣维南原理加以简化。
圣维南原理在钢管混凝土拱桥分析中的应用,能够得到合理的结果,优化了结构性能。
圣维南原理在材料力学中也有应用,在工程实际中经常要计算连接件,如铆钉,螺栓,键等,由于构件本身尺寸较小,变形比较复杂,采用计算其名义应力,然后根据直接的试验结果,确定其相应的许用应力,来进行强度计算。
二、论述题1、任何一个有限元分析问题都是空间问题,什么情况下可以简化为平面问题?轴对称问题?空间梁问题?为什么答:平面问题分为平面应力问题和平面应变问题,当研究对象一个方向的尺寸远小于另两个方向,外力和约束仅平行于板面作用而沿Z向不变,且仅有的三个应力分量是x、y的函数时,这样的空间问题就可以转换成平面应力问题;当研究对象一个方向的尺寸远大于另外两个方向的尺寸且沿长度方向几何形状和尺寸不变,外力平行于横截面作用而沿长度z方向不变,任意一横截面均可视为对称面,这样的空间问题就可以转换成平面应变问题,如挡土墙、重力坝。
如果弹性体的几何形状、约束状态以及外载荷都对称于某一根轴(过该轴的任意平面都是对称平面),那么弹性体的所有应力、应变和位移也就对称与这根轴,这样的问题就可以转换为轴对称问题。
当构件的长度远大于其横截面尺寸,如传动轴、梁杆等,这样的问题就可以转换为空间梁问题。
2、阐述有限元的基本思想。
试从有限元程序开发和采用成熟软件两方面进行有限元分析答:有限元的基本思想是将结构离散化,用有限个容易分析的单元来表示复杂的对象,单元之间通过有限个结点相互连接,然后根据变形协调条件综合求解。
由于单元的数目是有限的,接点的数目也是有限的,所以称为有限单元法。
有限元程序开发:力学模型的确定;结构的离散化;计算载荷的等效节点力;计算各单元的刚度矩阵;组集整体刚度矩阵;施加便捷约束条件;求解降阶的有限元基本方程;求解单元应力;计算结果的输出。
成熟软件①前处理器:定义单元类型;定义材料属性;建模;约束,载荷施加等②求解器。
单元刚度矩阵生成;约束处理;线性方程组,单元位移及应力等求解③后处理器:结果查询与显示;验算等。
3、有了本门课程的有限元分析技术基础,如果以后涉足机械方面的有限元分析,你觉得应从哪些方面深化学习和开展工作,具体采用哪些方式?答:一、学习数学基础知识(1)矩阵论(2)泛函和变分(3)数值方法(4)数学分析二、学习程序实现和使用(1)程序实现,(2)程序使用三、要有一定的力学基础熟练理论力学,材料力学、结构力学,特别是弹性力学,4.有限元软件:ansys、Adina system、ABAQUS、cosmos、LS-DYNA5.有限元优点:分析对象集合适应性强,适用范围广,较好的稳定性和收敛性,便于计算机处理二.有限元的基本思想?协调有限元的结果和原因?如何提高有限元的计算精度?答:(1)基本思想是把连续的集合机构离散成有限个单元,并在每一个单元内设定有限个节点,从而将连续体看作是仅在节点处相连接的一组单元的集合体,同时选定场函数的节点值作为基本未知量,并在每一个单元中假定一个近似插值函数,以表示单元中场函数的分布规律,建立有限个方程组,将无限个自由度问题转为离散域中有限个自由度的问题。
(2)协调的有限元的解一定收敛,它的位移解答一般都小于精确解,即协调单元的刚度比实际值大。
结果是单元位移函数能保证在单元内和单元外边界上位移和应变都连续。
(3)选择合适单元,细分网格,缩小网格尺寸,提高位移模式阶次。
三. 关于位移模式(函数)的收敛准则是什么?给某种单元,写出其位移函数,并讨论收敛性?位移函数项数和阶次是怎么选取的?答(1)完备性要求。
如果出现在泛函中场函数的最高阶导数是m阶,则有限元解收敛的条件之一是单元内场函数的试探函数至少是m次完全多项式。
协调性要求。
如果出现在泛函中的最高阶导数是m阶,即在相邻单元的交界面上应有函数直至m-1阶的连续导数。
(2)必须包含刚体位移a1 a4,常应变a2,3,5,6,相邻单元之间位移必须协调。
(3)原则是位移函数中待定系数的个数应等于单元节点自由度的个数,根据PASCAL三角形有低阶到高阶按顺序、对称选择。
四.弹性薄板的假设是什么?薄板挠度的位移多项式是这么选取的?选取的原因和结果是什么?答.(1)中面的法线在变形前后仍然保持和中面垂直的直法线假设;忽略二阶及更高阶变形分量;平板厚度远小于另外两个方向的尺寸;假定平板内各层互不挤压。
(2)(3)挠度位移函数模式的选取及原因:因为单元节点位移(每个结点的挠度和绕两坐标轴的转角)共计12个,故称12自由度薄板单元,故广义坐标法的位移模式可取为:四次项之所以选取和,是为了保证坐标互换时位移模式对坐标具有不变性以及扭率和曲率都具有相同的阶次。
五.等参元的基本思想和特点?什么是等参变换?有什么条件?答(1)用子单元与母单元之间的坐标映射和位移映射,将一个不规则单元转换成一个规则单元.特点:不管积分形式的矩阵表示的被积函数如何复杂,仍可方便的采用标准化的数值积分方法计算(2)将自然坐标系内形状规则的单元变换成总体笛卡尔坐标内的形状扭曲的单元,子单元与母单元之间的坐标映射和位移映射采用相同的形函数和具有相同的节点位移个数,称为等参变换.(3)雅克比行列式不为0;单元不能过分歪曲而导致dηξ和任意两点发生共线的情况;任意两个节点不能退化成一个节点。
六.数值积分是这么选取积分阶次的?采用高斯积分,减塑积分,精确积分方案的特点和原因?答(1)通常选用高斯积分。
积分阶次的选择采用数值积分代替精确积分时,积分阶数的选取应适当,因为它直接影响计算精度,计算工作量。
主要从两方面考虑:1.保证积分的精度,不损失收敛性;2.避免引起结构总刚度矩阵的奇异性,导致计算的失败(2)当高斯积分阶数等于被积函数所有项次精确积分所需要阶数的积分方案,称为精确积分。
当单元尺寸不断减小时,有限元解单调收敛于精确解,可以保证刚度阵非奇异。
高斯积分阶数低于被积函数所有项次精确积分所需阶数的积分方案,称为减缩积分。
使用减缩积分,必须检查总刚度矩阵的非奇异性,使用减缩积分不仅可以减小计算量,还可以对计算结果有所改进。
七.怎样的有限元网格划分是不合理的?介绍几种不合理划分的情况,解释为什么不合理?答网格数量过多或者过少;网格疏密程度错误;单元阶次选择不当;网格质量不高;网格布局不对称;节点和单元编号不合理。
任意单元的顶点必须同时也是相邻单元的顶点,而不能是相邻单元的内节点;同一单元的个边长不宜相差太大,即不能出现太大的钝角和锐角。
第一章;1-1答:错;1-3答:可以,有限元可以使用无网格法;第二章;2-1答:主要功能模块:结构分析、高度非线性瞬态;GUI方式下的六个窗口的功能和特点:(1)应用命;(2)主菜单:包括分析过程的主要命令,如建立模块;(5)输出窗口:叙述了输入命令执行的结果;2-2答:模型控制工具条中的“自由按钮”;2-3答:①建立实际工程问题的计算模型:利用几何;②选择第一章1-1答:错。
1-2答:错,加权余量法可以尤其适合于具有连续场的非力学问题,如声、电、热和磁学问题的有限元方程的建立。
1-3答:可以,有限元可以使用无网格法。
无网格方法(Mesh-less method)是在数值计算中不需要生成网格,而是按照一些任意分布的坐标点构造插值函数离散控制方程,就可方便地模拟各种复杂形状的流场。
第二章2-1答:主要功能模块:结构分析、高度非线性瞬态动力分析(NSYS/LS—DYNA)、热分析、电磁分析、流体动力学分析、声学分析、压电分析、多场耦合分析、优化设计及设计灵敏度分析等GUI方式下的六个窗口的功能和特点:(1)应用命令菜单:包含各种应用命令,如文件控制、对象选择等。
(2)主菜单:包括分析过程的主要命令,如建立模块、施加载荷和设置边界条件等。
(3)图形窗口:显示使用者所建立的模块机查看结果分析。
(4)输入窗口:该窗口可以输入命令,同时可监视命令的历程。
(5)输出窗口:叙述了输入命令执行的结果。
(6)模型控制工具条:该控制工具条窗口内的按钮控制图形的缩放、平移和旋转。
2-2答:模型控制工具条中的“自由按钮”。
2-3答:①建立实际工程问题的计算模型:利用几何、载荷的对称性简化模型,建立等效模型,确定边界条件;②选择合适的建模和分析工具,侧重考虑一下几个方面:物理场耦合问题、大变形、网格重画分③前处理(Preprocessing):建立几何模型进行有限单元划分与网格控制④求解(Solution):给定约束(Constrain t)和施加载荷(Load)、求解方法选择、计算参数设定⑤后处理(Postprocessing):后处理的目的在与分析计算模型是否合理,得出结论2-4答:网格疏密是指在结构不同部位采用大小不同的单元,这是为了适应计算数据的分布特点。