2013年试题及部分答案
- 格式:doc
- 大小:211.00 KB
- 文档页数:9

2013年普通高等学校招生全国统一考试语文本试题卷共8页,六大题23小题。
全卷满分150分。
考试用时150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.非选择题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、语文基础知识(共15分,共5小题,每小题3分)1.下列各组词语中,加点字的注音全都正确的一组是A.踹(chuài)水竞(jìnɡ)赛蘸(zhàn)酒擂(léi)鼓助威B.跋涉(shè)陡(dǒu)峭攀登(dēnɡ)餐霜饮雪(xiě)C.善(shàn)良谦逊(sùn)璞(pú)玉不事雕琢(zhuó)D.荆棘(jí)飘泊(bó)青苔(tāi)红漆(qī)雕花2.下列各组词语中,没有错别字的一组是A.彷徨愁怨寂寥静默凄婉惆伥B.顾盼精捍步履稳健风神潇洒C.睿智禀赋崇高品质趋善避恶D.辩难商榷典藉满架旁稽博采3.依次填入下列横线处的词语,最恰当的一组是①宋人画雪常不用铅粉,把背景用墨衬黑,一层层,留出山头的白,树梢的白,甚至花蕾上的白,虚实映衬,意境悠远。
②因为睡不着,打开窗帘,遥望夜空,满天,斜月晶莹,薄雾似轻纱漫卷,。
我思念那个小山村,那个让我魂牵梦绕的地方!A.而是点染星汉如梦如幻B.总是浸染星云如诗如画C.却是绘染星光诗意盎然D.只是渲染星斗诗意朦胧4.下列各项中,没有语病的一项是A.《美丽中国》以歌舞为主,融入京剧演唱、茶艺表演、少林武术等元素,加上奇幻的灯光,震撼的音响,一幅美丽中国的大写意,声光舞影流溢着浓郁的中国情。

2013乐理试题及答案2013年乐理试题及答案一、音乐素养部分1. 音乐是一门多层次的艺术形式,它通过音乐元素的运用来表达情感和思想。
请你分析以下两段音乐的风格特点并比较它们传达的情感。
a) 摇滚乐曲《We Will Rock You》该曲风格属于摇滚乐,强调节奏的冲击力和吉他的独奏。
由于它采用了简单的曲调和鼓点,给人一种霸气和勇敢的感觉。
这首歌曲的情感表达能激发人们的振奋和力量。
b) 古典音乐《第五交响曲第一乐章》(贝多芬)该乐章属于古典音乐,曲调较为庄重,运用了管弦乐器的丰富变化。
通过乐器的合奏和剧烈的变化,表达了一种壮丽和雄伟的情感。
这段音乐让人感受到宏大和深沉的力量。
2. 音乐中的节奏和速度对音乐的表达起着至关重要的作用。
请你选择一首你最喜欢的歌曲,分析其中的节奏和速度是如何影响你产生情感共鸣的。
我选择的歌曲是《Let It Be》。
该曲的节奏稳定、舒缓,速度适中。
通过这种节奏和速度的运用,歌曲传递出一种安静和宽慰的情感,让人感受到内心的宁静和接受。
这样的音乐让我感到放松和平静,也帮助我排解压力和疲惫。
二、乐理知识部分1. 音符的时值是指音符的持续时间。
请你简要介绍下列音符时值的定义和符号表示。
a) 全音符全音符时值为四个拍子,用一个空心实心笔画的椭圆形表示。
b) 二分音符二分音符时值为两个拍子,用一个空心实心笔画的椭圆形,并在其右侧加一根短竖线表示。
c) 四分音符四分音符时值为一个拍子,用一个空心实心笔画的椭圆形表示。
2. 和声是指两个或更多音符同时发声产生的效果。
请你简要描述以下两种常见的和声类型。
a) 和弦和弦是指两个或更多个音符同时演奏或唱出,通过和弦的演奏可以产生丰富的音响效果和和谐感。
常见的和弦有三和弦、七和弦、四和弦等等。
b) 和声进行和声进行是指在音乐中通过不同和弦的串联和变化来表达情感和推动音乐的发展。
这样的和声进行可以给音乐带来层次感和变化,增加听众的兴趣和情绪共鸣。

2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)语文试题本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成第1~3题。
20世纪后期,陕西凤雏村出土了刻有“凤”字的甲骨四片,这些“凤”字的形体大致相同,均为头上带有象征神权或王权的抽象化了的毛角的短尾鸟。
东汉许慎《说文解字》云:“ ,凤属,神鸟也。
……江中有 ,似凫而大,赤目。
”据此,古代传说中鸣于岐山、兆示周王朝兴起的神鸟凤凰,其原型应该是一种形象普通、类似水鸭的短尾水鸟。
那么,普通的短尾鸟“凤”为何在周代变为华冠长尾、祥瑞美丽的神鸟了呢?我们看到,在商代早期和中期的青铜器纹饰中,只有鸟纹而没有凤纹,真正的凤形直到殷商晚期才出现,而且此时是华冠短尾鸟和华丽而饰有眼翎的长尾鸟同时出现,可见“凤”是由鸟演变而来的。
综观甲骨文和商代青铜器,凤鸟的演变应该是鸟在先,凤在后,贯穿整个商代的不是凤而是鸟。
“天命玄鸟,降而生商”,在商人的历史中鸟始终扮演着图腾始祖的重要角色。
《左传》记载郯子说:“我高祖少皞挚之立也,凤鸟适至,故纪于鸟,为鸟师而鸟名。
凤鸟氏历正也……九扈为九农正。
”凤鸟氏成为“历正”之官,是由于它知天时,九扈成为“九农正”,也是由于它们带来了耕种、耘田和收获的信息。
殷人先祖之所以“鸟师而鸟名”,应该是由于这些随着信风迁徙的鸟,给以少皞为首的商人的农业生产带来了四季节令的消息。
对凤鸟的崇拜起于商代,其鼎盛却在周代。
正是在周代,“凤”完成了其发展程序中最后也是最重要的环节:变为神鸟凤凰。
许多历史资料记载了周王室在克商前后对“天命”的重视。
《尚书》“周书”十二篇中大量出现的“命”字多指天命,“殷革夏命”也是常见的语句。
武王在甲子日牧野之战结束后,紧接着就“不革服”“格于庙”(来不及换衣服就到神庙参拜),这个“庙”自然不可能是周庙,而是商人的神庙。
这说明周王室急于把商人的正统接过来,成为中原合法的统治者。

绝密★启用前2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)英语本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷时,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
不能答在试卷上,否则无效。
第一部分英语知识运用(共两节,满分45分)第一节单项填空(共15小题:每小题1分,满分15分)从A、B、C、D四个选项中选出可以填入空白处的最佳选项,并在答题卡上将该选项涂黑。
例:It is generally considered unwise to give a child he or she wants.A. howeverB. whateverC. whicheverD. whenever答案是B。
1.--I'm sorry I made a mistake!-- Nobody is perfect.A. Take your timeB. You're rightC.Whatever you sayD. Take it easy2. Would you like to with us to the film tonight?A. come alongB. come offC. come acrossD. come through3. I was glad to meet Jenny again, I didn't want to spend all day with her.A. butB. andC.soD.or4. When I arrived, Bryan took me to see the house_ I would be staying.A. whatB. whenC. whereD. which5.I got to the office earlier that day, the 7:30 train from PaddingtonA.caughtB. to have caughtC. to catchD. having caught6. Since nobody gave him any help, he have done the research on his own.A. canB. mustC. wouldD. need7. We very early so we packed the night before.A. leaveB. had leftC. were leavingD.have left8. The watch was very good, and he 20 percent down for it.A. a good oneB. a better oneC. the best oneD. a best one10. It was only after he had read the papers Mr. Gross realized the task before him was extremely difficult to complete.A.whenB. thatC. whichD. what11 A serious study of physics is impossible some knowledge of mathematics.A. againstB. beforeC. beyondD. without12. Only by increasing the number of doctors by 50 percent properly in this hospital.A. can be the patientsB. can the patients be treatedC. the patients can be treatedD.treated can be the patients13.Four and half hours of discussion took us up to midnight,and break for cheese,chocolate and tea with sugar.A.a;aB. the; theC.不填;theD.a;不填14. It's an either-or situation - we can buy a new car this year or we can go on holiday but we can’t do.A.othersB. eitherC.anotherD. both15. -Are you sure you won't come for a drink with us?- ,if you insistA. Not at allB. It dependsC. All right thenD.I don't care第二节完形填空(共20小题;每小题1.5分,满分30分)阅读下面短文,从短文后面各题锁哥的四个选项(A、B、C 和D)中选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。

2013年高考全国2卷英语试题及答案2013年普通高等学校招生全国统一考试(全国2卷)英语试题第I卷(选择题;满分115分)第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
选出最佳选项,每段对话仅读一遍。
1. How many apples did the man give those homeless men?A. 4.B. 6.C.8.2. What does the woman mean?A. She would invite Jenny to her party.B. She has something else to do.C. She isn’t invited to the party.3. What is the woman?A. A teacher.B. A student.C.A taxi driver.4. Who saved the two boys ?A. Two young men.B. Their mothers.C. The man.5. What happened to the man ?A. He was late for work today.B. He was scolded by his manager.C. He was laughed at by his colleagues.第二节(共15小题:每小题1.5分,满分22.5分)听下面5段对话。
选出最佳选项。
每段对话读两遍。
听第6段材料,回答6、7题。
6.Who likes blue best according to the woman?A. Jenny.B. Tom.C. Jim.7.What do the speakers want to buy?A. A blue shirt in size 8.B. A white shirt in size10. C. A white shirt in size 9.听第7段材料,回答第8、9题8. What did the woman do during the summer?A. She went to the beach with her aunt.B. She went to the countryside alone.C. She went to her grandparents’ farm.9. What does the man think of his vacation?A. Great.B. Disappointing.C. Too short.听第8段材料,回答第10至12题。
2013年全国统一高考数学试卷(理科)(新课标Ⅰ)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)已知集合A={x|x2﹣2x>0},B={x|﹣<x<},则()A.A∩B=∅B.A∪B=R C.B⊆A D.A⊆B2.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4B.C.4D.3.(5分)为了解某地区中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单的随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样4.(5分)已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y=B.y=C.y=±x D.y=5.(5分)执行程序框图,如果输入的t∈[﹣1,3],则输出的s属于()A.[﹣3,4]B.[﹣5,2]C.[﹣4,3]D.[﹣2,5] 6.(5分)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为()A.B.C.D.7.(5分)设等差数列{a n}的前n项和为S n,若S m﹣1=﹣2,S m=0,S m+1=3,则m=()A.3B.4C.5D.68.(5分)某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π9.(5分)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=()A.5B.6C.7D.810.(5分)已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为()A.B.C.D.11.(5分)已知函数f(x)=,若|f(x)|≥ax,则a的取值范围是()A.(﹣∞,0]B.(﹣∞,1]C.[﹣2,1]D.[﹣2,0] 12.(5分)设△A n B n C n的三边长分别为a n,b n,c n,△A n B n C n的面积为S n,n=1,2,3…若b1>c1,b1+c1=2a1,a n+1=a n,,,则()A.{S n}为递减数列B.{S n}为递增数列C.{S2n﹣1}为递增数列,{S2n}为递减数列D.{S2n﹣1}为递减数列,{S2n}为递增数列二.填空题:本大题共4小题,每小题5分.13.(5分)已知两个单位向量,的夹角为60°,=t+(1﹣t).若•=0,则t=.14.(5分)若数列{a n}的前n项和为S n=a n+,则数列{a n}的通项公式是a n=.15.(5分)设当x=θ时,函数f(x)=sinx﹣2cosx取得最大值,则cosθ=.16.(5分)若函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,则f(x)的最大值为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)如图,在△ABC中,∠ABC=90°,AB=,BC=1,P为△ABC内一点,∠BPC=90°.(1)若PB=,求PA;(2)若∠APB=150°,求tan∠PBA.18.(12分)如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.19.(12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立.(Ⅰ)求这批产品通过检验的概率;(Ⅱ)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.20.(12分)已知圆M:(x+1)2+y2=1,圆N:(x﹣1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P 的半径最长时,求|AB|.21.(12分)已知函数f(x)=x2+ax+b,g(x)=e x(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.(Ⅰ)求a,b,c,d的值;(Ⅱ)若x≥﹣2时,f(x)≤kg(x),求k的取值范围.四、请考生在第22、23、24题中任选一道作答,并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分,不涂,按本选考题的首题进行评分.22.(10分)(选修4﹣1:几何证明选讲)如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.(Ⅰ)证明:DB=DC;(Ⅱ)设圆的半径为1,BC=,延长CE交AB于点F,求△BCF外接圆的半径.23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).24.已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当x∈[﹣,]时,f(x)≤g(x),求a的取值范围.2013年全国统一高考数学试卷(理科)(新课标Ⅰ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)已知集合A={x|x2﹣2x>0},B={x|﹣<x<},则()A.A∩B=∅B.A∪B=R C.B⊆A D.A⊆B【考点】1D:并集及其运算;73:一元二次不等式及其应用.【专题】59:不等式的解法及应用;5J:集合.【分析】根据一元二次不等式的解法,求出集合A,再根据的定义求出A∩B和A∪B.【解答】解:∵集合A={x|x2﹣2x>0}={x|x>2或x<0},∴A∩B={x|2<x<或﹣<x<0},A∪B=R,故选:B.【点评】本题考查一元二次不等式的解法,以及并集的定义,属于基础题.2.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4B.C.4D.【考点】A5:复数的运算.【专题】5N:数系的扩充和复数.【分析】由题意可得z==,再利用两个复数代数形式的乘除法法则化简为+i,由此可得z的虚部.【解答】解:∵复数z满足(3﹣4i)z=|4+3i|,∴z====+i,故z的虚部等于,故选:D.【点评】本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,属于基础题.3.(5分)为了解某地区中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单的随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样【考点】B3:分层抽样方法.【专题】21:阅读型.【分析】若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样.【解答】解:我们常用的抽样方法有:简单随机抽样、分层抽样和系统抽样,而事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.了解某地区中小学生的视力情况,按学段分层抽样,这种方式具有代表性,比较合理.故选:C.【点评】本小题考查抽样方法,主要考查抽样方法,属基本题.4.(5分)已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y=B.y=C.y=±x D.y=【考点】KC:双曲线的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】由离心率和abc的关系可得b2=4a2,而渐近线方程为y=±x,代入可得答案.【解答】解:由双曲线C:(a>0,b>0),则离心率e===,即4b2=a2,故渐近线方程为y=±x=x,故选:D.【点评】本题考查双曲线的简单性质,涉及的渐近线方程,属基础题.5.(5分)执行程序框图,如果输入的t∈[﹣1,3],则输出的s属于()A.[﹣3,4]B.[﹣5,2]C.[﹣4,3]D.[﹣2,5]【考点】3B:分段函数的解析式求法及其图象的作法;EF:程序框图.【专题】27:图表型;5K:算法和程序框图.【分析】本题考查的知识点是程序框图,分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算一个分段函数的函数值,由条件为t<1我们可得,分段函数的分类标准,由分支结构中是否两条分支上对应的语句行,我们易得函数的解析式.【解答】解:由判断框中的条件为t<1,可得:函数分为两段,即t<1与t≥1,又由满足条件时函数的解析式为:s=3t;不满足条件时,即t≥1时,函数的解析式为:s=4t﹣t2故分段函数的解析式为:s=,如果输入的t∈[﹣1,3],画出此分段函数在t∈[﹣1,3]时的图象,则输出的s属于[﹣3,4].故选:A.【点评】要求条件结构对应的函数解析式,要分如下几个步骤:①分析流程图的结构,分析条件结构是如何嵌套的,以确定函数所分的段数;②根据判断框中的条件,设置分类标准;③根据判断框的“是”与“否”分支对应的操作,分析函数各段的解析式;④对前面的分类进行总结,写出分段函数的解析式.6.(5分)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为()A.B.C.D.【考点】LG:球的体积和表面积.【专题】11:计算题;5F:空间位置关系与距离.【分析】设正方体上底面所在平面截球得小圆M,可得圆心M为正方体上底面正方形的中心.设球的半径为R,根据题意得球心到上底面的距离等于(R﹣2)cm,而圆M的半径为4,由球的截面圆性质建立关于R的方程并解出R=5,用球的体积公式即可算出该球的体积.【解答】解:设正方体上底面所在平面截球得小圆M,则圆心M为正方体上底面正方形的中心.如图.设球的半径为R,根据题意得球心到上底面的距离等于(R﹣2)cm,而圆M的半径为4,由球的截面圆性质,得R2=(R﹣2)2+42,解出R=5,∴根据球的体积公式,该球的体积V===.故选:A.【点评】本题给出球与正方体相切的问题,求球的体积,着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识,属于中档题.7.(5分)设等差数列{a n}的前n项和为S n,若S m﹣1=﹣2,S m=0,S m+1=3,则m=()A.3B.4C.5D.6【考点】83:等差数列的性质;85:等差数列的前n项和.【专题】11:计算题;54:等差数列与等比数列.【分析】由a n与S n的关系可求得a m+1与a m,进而得到公差d,由前n项和公式及S m=0可求得a1,再由通项公式及a m=2可得m值.【解答】解:a m=S m﹣S m﹣1=2,a m+1=S m+1﹣S m=3,所以公差d=a m﹣a m=1,+1S m==0,m﹣1>0,m>1,因此m不能为0,得a1=﹣2,所以a m=﹣2+(m﹣1)•1=2,解得m=5,另解:等差数列{a n}的前n项和为S n,即有数列{}成等差数列,则,,成等差数列,可得2•=+,即有0=+,解得m=5.又一解:由等差数列的求和公式可得(m﹣1)(a1+a m﹣1)=﹣2,m(a1+a m)=0,(m+1)(a1+a m+1)=3,可得a1=﹣a m,﹣2a m+a m+1+a m+1=+=0,解得m=5.故选:C.【点评】本题考查等差数列的通项公式、前n项和公式及通项a n与S n的关系,考查学生的计算能力.8.(5分)某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π【考点】L!:由三视图求面积、体积.【专题】16:压轴题;27:图表型.【分析】三视图复原的几何体是一个长方体与半个圆柱的组合体,依据三视图的数据,得出组合体长、宽、高,即可求出几何体的体积.【解答】解:三视图复原的几何体是一个长方体与半个圆柱的组合体,如图,其中长方体长、宽、高分别是:4,2,2,半个圆柱的底面半径为2,母线长为4.∴长方体的体积=4×2×2=16,半个圆柱的体积=×22×π×4=8π所以这个几何体的体积是16+8π;故选:A.【点评】本题考查了几何体的三视图及直观图的画法,三视图与直观图的关系,柱体体积计算公式,空间想象能力9.(5分)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=()A.5B.6C.7D.8【考点】DA:二项式定理.【专题】5P:二项式定理.【分析】根据二项式系数的性质求得a和b,再利用组合数的计算公式,解方程13a=7b求得m的值.【解答】解:∵m为正整数,由(x+y)2m展开式的二项式系数的最大值为a,以及二项式系数的性质可得a=,同理,由(x+y)2m+1展开式的二项式系数的最大值为b,可得b==.再由13a=7b,可得13=7,即13×=7×,即13=7×,即13(m+1)=7(2m+1),解得m=6,故选:B.【点评】本题主要考查二项式系数的性质的应用,组合数的计算公式,属于中档题.10.(5分)已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为()A.B.C.D.【考点】K3:椭圆的标准方程.【专题】5D:圆锥曲线的定义、性质与方程.【分析】设A(x1,y1),B(x2,y2),代入椭圆方程得,利用“点差法”可得.利用中点坐标公式可得x1+x2=2,y1+y2=﹣2,利用斜率计算公式可得==.于是得到,化为a2=2b2,再利用c=3=,即可解得a2,b2.进而得到椭圆的方程.【解答】解:设A(x1,y1),B(x2,y2),代入椭圆方程得,相减得,∴.∵x1+x2=2,y1+y2=﹣2,==.∴,化为a2=2b2,又c=3=,解得a2=18,b2=9.∴椭圆E的方程为.故选:D.【点评】熟练掌握“点差法”和中点坐标公式、斜率的计算公式是解题的关键.11.(5分)已知函数f(x)=,若|f(x)|≥ax,则a的取值范围是()A.(﹣∞,0]B.(﹣∞,1]C.[﹣2,1]D.[﹣2,0]【考点】7E:其他不等式的解法.【专题】16:压轴题;59:不等式的解法及应用.【分析】由函数图象的变换,结合基本初等函数的图象可作出函数y=|f(x)|的图象,和函数y=ax的图象,由导数求切线斜率可得l的斜率,进而数形结合可得a的范围.【解答】解:由题意可作出函数y=|f(x)|的图象,和函数y=ax的图象,由图象可知:函数y=ax的图象为过原点的直线,当直线介于l和x轴之间符合题意,直线l为曲线的切线,且此时函数y=|f(x)|在第二象限的部分解析式为y=x2﹣2x,求其导数可得y′=2x﹣2,因为x≤0,故y′≤﹣2,故直线l的斜率为﹣2,故只需直线y=ax的斜率a介于﹣2与0之间即可,即a∈[﹣2,0]故选:D.【点评】本题考查其它不等式的解法,数形结合是解决问题的关键,属中档题.12.(5分)设△A n B n C n的三边长分别为a n,b n,c n,△A n B n C n的面积为S n,n=1,2,3…若b1>c1,b1+c1=2a1,a n+1=a n,,,则()A.{S n}为递减数列B.{S n}为递增数列C.{S2n﹣1}为递增数列,{S2n}为递减数列D.{S2n﹣1}为递减数列,{S2n}为递增数列【考点】82:数列的函数特性;8H:数列递推式.【专题】16:压轴题;54:等差数列与等比数列;55:点列、递归数列与数学归纳法.=a n可知△A n B n C n的边B n C n为定值a1,由b n+1+c n+1﹣【分析】由a n+12a1=及b1+c1=2a1得b n+c n=2a1,则在△A n B n C n中边长B n C n=a1为定值,另两边A n C n、A n B n的长度之和b n+c n=2a1为定值,由此可知顶点A n在以B n、C n为焦点的椭圆上,根据b n+1﹣c n+1=,得b n﹣c n=,可知n→+∞时b n→c n,据此可判断△A n B n C n的边B nC n的高h n随着n的增大而增大,再由三角形面积公式可得到答案.【解答】解:b1=2a1﹣c1且b1>c1,∴2a1﹣c1>c1,∴a1>c1,∴b1﹣a1=2a1﹣c1﹣a1=a1﹣c1>0,∴b1>a1>c1,又b1﹣c1<a1,∴2a1﹣c1﹣c1<a1,∴2c1>a1,∴,由题意,+a n,∴b n+1+c n+1﹣2a n=(b n+c n﹣2a n),∴b n+c n﹣2a n=0,∴b n+c n=2a n=2a1,∴b n+c n=2a1,由此可知顶点A n在以B n、C n为焦点的椭圆上,﹣c n+1=,∴=a1﹣b n,又由题意,b n+1﹣a1=,∴b n﹣a1=,∴b n+1∴,c n=2a1﹣b n=,∴[][]=[﹣]单调递增(可证当n=1时>0)故选:B.【点评】本题主要考查由数列递推式求数列通项、三角形面积海伦公式,综合考查学生分析解决问题的能力,有较高的思维抽象度,是本年度全国高考试题中的“亮点”之一.二.填空题:本大题共4小题,每小题5分.13.(5分)已知两个单位向量,的夹角为60°,=t+(1﹣t).若•=0,则t=2.【考点】9H:平面向量的基本定理;9O:平面向量数量积的性质及其运算.【专题】5A:平面向量及应用.【分析】由于•=0,对式子=t+(1﹣t)两边与作数量积可得=0,经过化简即可得出.【解答】解:∵,,∴=0,∴tcos60°+1﹣t=0,∴1=0,解得t=2.故答案为2.【点评】熟练掌握向量的数量积运算是解题的关键.14.(5分)若数列{a n}的前n项和为S n=a n+,则数列{a n}的通项公式是a n=(﹣2)n﹣1.【考点】88:等比数列的通项公式.【专题】54:等差数列与等比数列.【分析】把n=1代入已知式子可得数列的首项,由n≥2时,a n=S n﹣S n﹣1,可得数列为等比数列,且公比为﹣2,代入等比数列的通项公式分段可得答案.【解答】解:当n=1时,a1=S1=,解得a1=1当n≥2时,a n=S n﹣S n﹣1=()﹣()=,整理可得,即=﹣2,故数列{a n}从第二项开始是以﹣2为首项,﹣2为公比的等比数列,故当n≥2时,a n=(﹣2)n﹣1,经验证当n=1时,上式也适合,故答案为:(﹣2)n﹣1【点评】本题考查等比数列的通项公式,涉及等比数列的判定,属基础题.15.(5分)设当x=θ时,函数f(x)=sinx﹣2cosx取得最大值,则cosθ=﹣.【考点】GP:两角和与差的三角函数;H4:正弦函数的定义域和值域.【专题】16:压轴题;56:三角函数的求值.【分析】f(x)解析式提取,利用两角和与差的正弦函数公式化为一个角的正弦函数,由x=θ时,函数f(x)取得最大值,得到sinθ﹣2cosθ=,与sin2θ+cos2θ=1联立即可求出cosθ的值.【解答】解:f(x)=sinx﹣2cosx=(sinx﹣cosx)=sin(x﹣α)(其中cosα=,sinα=),∵x=θ时,函数f(x)取得最大值,∴sin(θ﹣α)=1,即sinθ﹣2cosθ=,又sin2θ+cos2θ=1,联立得(2cosθ+)2+cos2θ=1,解得cosθ=﹣.故答案为:﹣【点评】此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.16.(5分)若函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,则f(x)的最大值为16.【考点】57:函数与方程的综合运用;6E:利用导数研究函数的最值.【专题】11:计算题;16:压轴题;51:函数的性质及应用;53:导数的综合应用.【分析】由题意得f(﹣1)=f(﹣3)=0且f(1)=f(﹣5)=0,由此求出a=8且b=15,由此可得f(x)=﹣x4﹣8x3﹣14x2+8x+15.利用导数研究f(x)的单调性,可得f(x)在区间(﹣∞,﹣2﹣)、(﹣2,﹣2+)上是增函数,在区间(﹣2﹣,﹣2)、(﹣2+,+∞)上是减函数,结合f(﹣2﹣)=f(﹣2+)=16,即可得到f(x)的最大值.【解答】解:∵函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,∴f(﹣1)=f(﹣3)=0且f(1)=f(﹣5)=0,即[1﹣(﹣3)2][(﹣3)2+a•(﹣3)+b]=0且[1﹣(﹣5)2][(﹣5)2+a•(﹣5)+b]=0,解之得,因此,f(x)=(1﹣x2)(x2+8x+15)=﹣x4﹣8x3﹣14x2+8x+15,求导数,得f′(x)=﹣4x3﹣24x2﹣28x+8,令f′(x)=0,得x1=﹣2﹣,x2=﹣2,x3=﹣2+,当x∈(﹣∞,﹣2﹣)时,f′(x)>0;当x∈(﹣2﹣,﹣2)时,f′(x)<0;当x∈(﹣2,﹣2+)时,f′(x)>0;当x∈(﹣2+,+∞)时,f′(x)<0∴f(x)在区间(﹣∞,﹣2﹣)、(﹣2,﹣2+)上是增函数,在区间(﹣2﹣,﹣2)、(﹣2+,+∞)上是减函数.又∵f(﹣2﹣)=f(﹣2+)=16,∴f(x)的最大值为16.故答案为:16.【点评】本题给出多项式函数的图象关于x=﹣2对称,求函数的最大值.着重考查了函数的奇偶性、利用导数研究函数的单调性和函数的最值求法等知识,属于中档题.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)如图,在△ABC中,∠ABC=90°,AB=,BC=1,P为△ABC内一点,∠BPC=90°.(1)若PB=,求PA;(2)若∠APB=150°,求tan∠PBA.【考点】HP:正弦定理;HR:余弦定理.【专题】58:解三角形.【分析】(I)在Rt△PBC,利用边角关系即可得到∠PBC=60°,得到∠PBA=30°.在△PBA中,利用余弦定理即可求得PA.(II)设∠PBA=α,在Rt△PBC中,可得PB=sinα.在△PBA中,由正弦定理得,即,化简即可求出.【解答】解:(I)在Rt△PBC中,=,∴∠PBC=60°,∴∠PBA=30°.在△PBA中,由余弦定理得PA2=PB2+AB2﹣2PB•ABcos30°==.∴PA=.(II)设∠PBA=α,在Rt△PBC中,PB=BCcos(90°﹣α)=sinα.在△PBA中,由正弦定理得,即,化为.∴.【点评】熟练掌握直角三角形的边角关系、正弦定理和余弦定理是解题的关键.18.(12分)如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.【考点】LW:直线与平面垂直;LY:平面与平面垂直;MI:直线与平面所成的角.【专题】5F:空间位置关系与距离;5G:空间角.【分析】(Ⅰ)取AB的中点O,连接OC,OA1,A1B,由已知可证OA1⊥AB,AB ⊥平面OA1C,进而可得AB⊥A1C;(Ⅱ)易证OA,OA1,OC两两垂直.以O为坐标原点,的方向为x轴的正向,||为单位长,建立坐标系,可得,,的坐标,设=(x,y,z)为平面BB1C1C的法向量,则,可解得=(,1,﹣1),可求|cos <,>|,即为所求正弦值.【解答】解:(Ⅰ)取AB的中点O,连接OC,OA1,A1B,因为CA=CB,所以OC⊥AB,由于AB=AA1,∠BAA1=60°,所以△AA1B为等边三角形,所以OA1⊥AB,又因为OC∩OA1=O,所以AB⊥平面OA1C,又A1C⊂平面OA1C,故AB⊥A1C;(Ⅱ)由(Ⅰ)知OC⊥AB,OA1⊥AB,又平面ABC⊥平面AA1B1B,交线为AB,所以OC⊥平面AA1B1B,故OA,OA1,OC两两垂直.以O为坐标原点,的方向为x轴的正向,||为单位长,建立如图所示的坐标系,可得A(1,0,0),A1(0,,0),C(0,0,),B(﹣1,0,0),则=(1,0,),=(﹣1,,0),=(0,﹣,),设=(x,y,z)为平面BB1C1C的法向量,则,即,可取y=1,可得=(,1,﹣1),故cos<,>==,又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值,故直线A1C与平面BB1C1C所成角的正弦值为:.【点评】本题考查直线与平面所成的角,涉及直线与平面垂直的性质和平面与平面垂直的判定,属难题.19.(12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立.(Ⅰ)求这批产品通过检验的概率;(Ⅱ)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.【考点】CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】5I:概率与统计.【分析】(Ⅰ)设第一次取出的4件产品中恰有3件优质品为事件A1,第一次取出的4件产品全是优质品为事件A2,第二次取出的4件产品全是优质品为事件B1,第二次取出的1件产品是优质品为事件B2,这批产品通过检验为事件A,依题意有A=(A1B1)∪(A2B2),且A1B1与A2B2互斥,由概率得加法公式和条件概率,代入数据计算可得;(Ⅱ)X可能的取值为400,500,800,分别求其概率,可得分布列,进而可得期望值.【解答】解:(Ⅰ)设第一次取出的4件产品中恰有3件优质品为事件A1,第一次取出的4件产品全是优质品为事件A2,第二次取出的4件产品全是优质品为事件B1,第二次取出的1件产品是优质品为事件B2,这批产品通过检验为事件A,依题意有A=(A1B1)∪(A2B2),且A1B1与A2B2互斥,所以P(A)=P(A1B1)+P(A2B2)=P(A1)P(B1|A1)+P(A2)P(B2|A2)==(Ⅱ)X可能的取值为400,500,800,并且P(X=800)=,P(X=500)=,P(X=400)=1﹣﹣=,故X的分布列如下:X 400 500 800P故EX=400×+500×+800×=506.25【点评】本题考查离散型随机变量及其分布列涉及数学期望的求解,属中档题.20.(12分)已知圆M:(x+1)2+y2=1,圆N:(x﹣1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P 的半径最长时,求|AB|.【考点】J3:轨迹方程;J9:直线与圆的位置关系.【专题】5B:直线与圆.【分析】(I)设动圆的半径为R,由已知动圆P与圆M外切并与圆N内切,可得|PM|+|PN|=R+1+(3﹣R)=4,而|NM|=2,由椭圆的定义可知:动点P的轨迹是以M,N为焦点,4为长轴长的椭圆,求出即可;(II)设曲线C上任意一点P(x,y),由于|PM|﹣|PN|=2R﹣2≤4﹣2=2,所以R ≤2,当且仅当⊙P的圆心为(2,0)R=2时,其半径最大,其方程为(x﹣2)2+y2=4.分①l的倾斜角为90°,此时l与y轴重合,可得|AB|.②若l的倾斜角不为90°,由于⊙M的半径1≠R,可知l与x轴不平行,设l与x轴的交点为Q,根据,可得Q(﹣4,0),所以可设l:y=k(x+4),与椭圆的方程联立,得到根与系数的关系利用弦长公式即可得出.【解答】解:(I)由圆M:(x+1)2+y2=1,可知圆心M(﹣1,0);圆N:(x﹣1)2+y2=9,圆心N(1,0),半径3.设动圆的半径为R,∵动圆P与圆M外切并与圆N内切,∴|PM|+|PN|=R+1+(3﹣R)=4,而|NM|=2,由椭圆的定义可知:动点P的轨迹是以M,N为焦点,4为长轴长的椭圆,∴a=2,c=1,b2=a2﹣c2=3.∴曲线C的方程为(x≠﹣2).(II)设曲线C上任意一点P(x,y),由于|PM|﹣|PN|=2R﹣2≤3﹣1=2,所以R≤2,当且仅当⊙P的圆心为(2,0)R=2时,其半径最大,其方程为(x﹣2)2+y2=4.①l的倾斜角为90°,则l与y轴重合,可得|AB|=.②若l的倾斜角不为90°,由于⊙M的半径1≠R,可知l与x轴不平行,设l与x轴的交点为Q,则,可得Q(﹣4,0),所以可设l:y=k(x+4),由l于M相切可得:,解得.当时,联立,得到7x2+8x﹣8=0.∴,.∴|AB|===由于对称性可知:当时,也有|AB|=.综上可知:|AB|=或.【点评】本题综合考查了两圆的相切关系、直线与圆相切问题、椭圆的定义及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式等基础知识,需要较强的推理能力和计算能力及其分类讨论的思想方法.21.(12分)已知函数f(x)=x2+ax+b,g(x)=e x(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.(Ⅰ)求a,b,c,d的值;(Ⅱ)若x≥﹣2时,f(x)≤kg(x),求k的取值范围.【考点】3R:函数恒成立问题;6H:利用导数研究曲线上某点切线方程.【专题】16:压轴题;53:导数的综合应用.【分析】(Ⅰ)对f(x),g(x)进行求导,已知在交点处有相同的切线及曲线y=f (x)和曲线y=g(x)都过点P(0,2),从而解出a,b,c,d的值;(Ⅱ)由(I)得出f(x),g(x)的解析式,再求出F(x)及它的导函数,通过对k的讨论,判断出F(x)的最值,从而判断出f(x)≤kg(x)恒成立,从而求出k的范围.【解答】解:(Ⅰ)由题意知f(0)=2,g(0)=2,f′(0)=4,g′(0)=4,而f′(x)=2x+a,g′(x)=e x(cx+d+c),故b=2,d=2,a=4,d+c=4,从而a=4,b=2,c=2,d=2;(Ⅱ)由(I)知,f(x)=x2+4x+2,g(x)=2e x(x+1)设F(x)=kg(x)﹣f(x)=2ke x(x+1)﹣x2﹣4x﹣2,则F′(x)=2ke x(x+2)﹣2x﹣4=2(x+2)(ke x﹣1),由题设得F(0)≥0,即k≥1,令F′(x)=0,得x1=﹣lnk,x2=﹣2,①若1≤k<e2,则﹣2<x1≤0,从而当x∈(﹣2,x1)时,F′(x)<0,当x∈(x1,+∞)时,F′(x)>0,即F(x)在(﹣2,x1)上减,在(x1,+∞)上是增,故F(x)在[﹣2,+∞)上的最小值为F(x1),而F(x1)=﹣x1(x1+2)≥0,x≥﹣2时F(x)≥0,即f(x)≤kg(x)恒成立.②若k=e2,则F′(x)=2e2(x+2)(e x﹣e﹣2),从而当x∈(﹣2,+∞)时,F′(x)>0,即F(x)在(﹣2,+∞)上是增,而F(﹣2)=0,故当x≥﹣2时,F(x)≥0,即f(x)≤kg(x)恒成立.③若k>e2时,F′(x)>2e2(x+2)(e x﹣e﹣2),而F(﹣2)=﹣2ke﹣2+2<0,所以当x>﹣2时,f(x)≤kg(x)不恒成立,综上,k的取值范围是[1,e2].【点评】此题主要考查利用导数研究曲线上某点切线方程,函数恒成立问题,考查分类讨论思想,解题的关键是能够利用导数工具研究函数的性质,此题是一道中档题.四、请考生在第22、23、24题中任选一道作答,并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分,不涂,按本选考题的首题进行评分.22.(10分)(选修4﹣1:几何证明选讲)如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.(Ⅰ)证明:DB=DC;(Ⅱ)设圆的半径为1,BC=,延长CE交AB于点F,求△BCF外接圆的半径.【考点】NC:与圆有关的比例线段.【专题】5B:直线与圆.【分析】(I)连接DE交BC于点G,由弦切角定理可得∠ABE=∠BCE,由已知角平分线可得∠ABE=∠CBE,于是得到∠CBE=∠BCE,BE=CE.由已知DB⊥BE,可知DE为⊙O的直径,Rt△DBE≌Rt△DCE,利用三角形全等的性质即可得到DC=DB.(II)由(I)可知:DG是BC的垂直平分线,即可得到BG=.设DE的中点为O,连接BO,可得∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°.得到CF⊥BF.进而得到Rt△BCF的外接圆的半径=.【解答】(I)证明:连接DE交BC于点G.由弦切角定理可得∠ABE=∠BCE,而∠ABE=∠CBE,∴∠CBE=∠BCE,BE=CE.又∵DB⊥BE,∴DE为⊙O的直径,∠DCE=90°.∴△DBE≌△DCE,∴DC=DB.(II)由(I)可知:∠CDE=∠BDE,DB=DC.故DG是BC的垂直平分线,∴BG=.设DE的中点为O,连接BO,则∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°.∴CF⊥BF.∴Rt△BCF的外接圆的半径=.【点评】本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等、三角形的外接圆的半径等知识,需要较强的推理能力、分析问题和解决问题的能力.23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.【专题】11:计算题;35:转化思想;4R:转化法;5S:坐标系和参数方程.【分析】(1)曲线C1的参数方程消去参数t,得到普通方程,再由,能求出C1的极坐标方程.(2)曲线C2的极坐标方程化为直角坐标方程,与C1的普通方程联立,求出C1与C2交点的直角坐标,由此能求出C1与C2交点的极坐标.【解答】解:(1)将,消去参数t,化为普通方程(x﹣4)2+(y﹣5)2=25,即C1:x2+y2﹣8x﹣10y+16=0,将代入x2+y2﹣8x﹣10y+16=0,得ρ2﹣8ρcosθ﹣10ρsinθ+16=0.∴C1的极坐标方程为ρ2﹣8ρcosθ﹣10ρsinθ+16=0.(2)∵曲线C2的极坐标方程为ρ=2sinθ.∴曲线C2的直角坐标方程为x2+y2﹣2y=0,。

2013高考全国统一考试(精校版)全国一卷第一节单项填空 (共15小题,每小题1分,满分15分)从A、B、c、D四个选项中.选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
1.-- My name is Jonathan. Shall I spell it for you?--_____________.A.No problem.B. Of course, you should.C. If you don’t mindD. That’s all right.2. Wouldn’t it be ______ wonderful world if all nations lived in ______ peace with one another?A. a, /B. the, /C. a, theD. the, the3. The English ______ in England between AD450 and 1150 was very different from the English we_______ at present.A. speaking; spokenB. spoken; speakC. spoken; speakingD. speaking; are speaking4. We're excited to learn the news ________ China sent three astronauts into space between June and Augustthis year.A. whatB. whichC. thatD. as5. I _________glasses since I was in primary school and I hate them. They make me look like a bookworm.A. have wornB. have been wearingC. have been wornD. was wearing6. He is very popular among his students as he always tries to get them ________ in his lectures.A. interestingB. interestedC. being interestedD. to interest7. Susan was expecting her favourite singers, but to her disappointment, ______ appeared.A. someB. noneC. everyoneD. no one8. Although Rio knew little about marketing, he succeeded ______ other more well-informed managersfailed.A. asB. unlessC. whatD. where9. Clean water and fresh air are essential for our daily life, _______ we can’t liv e.A. by whichB. without whichC. thatD. on which10. —Can I borrow your car, Mum?—If you________.A. must B.can C.will D.may11.Only with the greatest of luck _______ to escape from the rising flood waters.A. managed sheB. she managedC. did she manageD. she did manage12. It was not until she took off her dark glasses _____ I realized she was a famous film star.A. whoB. thatC. whereD. before13. -- Have you ever been to the city of Beijing, our capital?-- Yes, only once. I ______ there only for two days.A. had stayedB. were stayingC. have stayedD. stayed14. Why this excellent newspaper allows such an article to be printed is _______ me.A. aboveB. outsideC. besideD. beyond15.----I’m sorry. I shouldn’t been so angry with you that day.----______. I was a bit out of control myself.A. That’s rightB. All rightC. Forget itD. Got it第二节完形填空(共20小.:每小1.5分.满分30分)阅读下面短文.从短文后各题所给的四个选项《A、B. C和D》中,选出可以填入空白处的最佳选项,并在答题卡上将该项小涂黑。

绝密★启用前2013年普通高等学校招生全国统一考试(全国卷)理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页.考试时间120分钟.满分150分.答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在第Ⅰ卷答题卡和第Ⅱ卷答题纸规定的位置. 参考公式:样本数据n x x x ,,21的标准差nx x x x x x s n 22221)()()(-++-+-=其中x 为样本平均数球的面积公式24R S π=第Ⅰ卷(选择题 共60分)注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上. 2.第Ⅰ卷只有选择题一道大题.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数ii++121(i 是虚数单位)的虚部是 A .23 B .21C .3D .1 2.已知R 是实数集,{}11,12+-==⎭⎬⎫⎩⎨⎧<=x y y N x xM ,则=M C N R A .)2,1(B .[]2,0C .∅D .[]2,13.现有10个数,其平均数是4,且这10个数的平方和是200,那么这个数组的标准差是 A .1 B .2 C .3 D .44.设n S 为等比数列{}n a 的前n 项和,0852=-a a ,则=24S S A .5 B .8 C .8- D .155.已知函数)62sin()(π-=x x f ,若存在),0(π∈a ,使得)()(a x f a x f -=+恒成立,则a的值是 A .6π B .3π C .4π D .2π 6.已知m 、n 表示直线,γβα,,表示平面,给出下列四个命题,其中真命题为 (1)βααβα⊥⊥⊂=则,,,m n n m (2)m n n m ⊥==⊥则,,,γβγαβα (3),,βα⊥⊥m m 则α∥β (4)βαβα⊥⊥⊥⊥则,,,n m n mA .(1)、(2)B .(3)、(4)C .(2)、(3)D .(2)、(4)7.已知平面上不共线的四点C B A O ,,,,若||,23BC -=等于A .1B .2C .3D .4 8.已知三角形ABC ∆的三边长成公差为2的等差数列,且最大角的正弦值为23,则这个三角形的周长是A .18B .21C .24D .15 9.函数xx x f 1lg )(-=的零点所在的区间是 A .(]1,0 B .(]10,1 C .(]100,10 D .),100(+∞ 10.过直线y x =上一点P 引圆22670x y x +-+=的切线,则切线长的最小值为A .22 B . 223 C .210 D .211.已知函数b ax x x f 2)(2-+=.若b a ,都是区间[]4,0内的数,则使0)1(>f 成立的概率是A .43 B .41 C .83D .8512.已知双曲线的标准方程为116922=-y x ,F 为其右焦点,21,A A 是实轴的两端点,设P 为双曲线上不同于21,A A 的任意一点,直线P A P A 21,与直线a x =分别交于两点N M ,,若题图第130=⋅FN FM ,则a 的值为A .916 B .59 C .925 D .516第Ⅱ卷(非选择题 共90分)注意事项:1. 请用0.5毫米的黑色签字笔将每题的答案填写在第Ⅱ卷答题纸的指定位置.书写的答案如需改动,要先划掉原来的答案,然后再写上新答案.2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效. 3. 第Ⅱ卷共包括填空题和解答题两道大题. 二、填空题:本大题共4小题,每小题4分,共16分. 13.如图所示的程序框图输出的结果为__________.14. 若一个底面是正三角形的三棱柱的正视图如下图所示,其顶点都在一个球面上,则该球的表面积为__________.15.地震的震级R 与地震释放的能量E 的关系为)4.11(lg 32-=E R .2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍. 16.给出下列命题: ①已知,,a b m都是正数,且bab a >++11,则a b <; ②已知()f x '是()f x 的导函数,若,()0x R f x '∀∈≥,则(1)(2)f f <一定成立; ③命题“x R ∃∈,使得2210x x-+<”的否定是真命题; ④“1,1≤≤y x 且”是“2≤+y x ”的充要条件.其中正确命题的序号是 .(把你认为正确命题的序号都填上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)第14题图已知向量),2cos 2sin 3()2cos ,1(y xx b x a +==→→与共线,且有函数)(x f y =.(Ⅰ)若1)(=x f ,求)232cos(x -π的值; (Ⅱ)在ABC ∆中,角C B A ,,,的对边分别是c b a ,,,且满足b c C a 2cos 2=+,求函数)(B f 的取值范围.18.(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,公差,50,053=+≠S S d 且1341,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设⎭⎬⎫⎩⎨⎧n n a b 是首项为1,公比为3的等比数列,求数列{}n b 的前n 项和n T .19.(本小题满分12分)已知四棱锥BCDE A -,其中1====BE AC BC AB ,2=CD ,ABC CD 面⊥,BE ∥CD ,F 为AD 的中点. (Ⅰ)求证:EF ∥面ABC ; (Ⅱ)求证:面ACD ADE 面⊥; (III )求四棱锥BCDE A -的体积.20.(本小题满分12分)在某种产品表面进行腐蚀性检验,得到腐蚀深度y 与腐蚀时间x 之间对应的一组数据:AB CDEF现确定的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再对被选取的2组数据进行检验.(Ⅰ)求选取的2组数据恰好不相邻的概率;(Ⅱ)若选取的是第2组和第5组数据,根据其它4组数据,求得y 关于x 的线性回归方程26139134ˆ+=x y,规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米,则认为得到的线性回归方程是可靠的,判断该线性回归方程是否可靠.21.(本小题满分12分)已知函数1)(2++=x bax x f 在点))1(,1(--f 的切线方程为03=++y x . (Ⅰ)求函数()f x 的解析式;(Ⅱ)设x x g ln )(=,求证:)()(x f x g ≥在),1[+∞∈x 上恒成立.22.(本小题满分14分)实轴长为34的椭圆的中心在原点,其焦点1,2,F F 在x 轴上.抛物线的顶点在原点O ,对称轴为y 轴,两曲线在第一象限内相交于点A ,且12AF AF ⊥,△12AF F 的面积为3.(Ⅰ)求椭圆和抛物线的标准方程;(Ⅱ)过点A 作直线l 分别与抛物线和椭圆交于C B ,,若2=,求直线l 的斜率k .参考答案及评分标准一.选择题(本大题共12小题,每小题5分,共60分.)B D B A D B B D BC C B二.填空题(本大题共4小题,每小题4分,共16分.)13.2 14.π31915. 2310 16. ①③ 三.解答题17.(本小题满分12分) 解:(Ⅰ)∵→a 与→b 共线∴yxx x 2cos 2cos2sin 31=+21)6sin()cos 1(21sin 232cos 2cos 2sin 32++=++=+=πx x x x x x y …………3分∴121)6sin()(=++=πx x f ,即21)6sin(=+πx …………………………………………4分211)6(sin 21)3(cos 2)3(2cos )232cos(22-=-+=--=-=-ππππx x x x…………………………………………6分 (Ⅱ)已知b c C a 2cos 2=+由正弦定理得:CA C A C C A C ABC C A sin cos 2cos sin 2sin cos sin 2)sin(2sin 2sin cos sin 2+=++==+∴21cos =A ,∴在ABC ∆中 ∠3π=A …………………………………………8分21)6sin()(++=πB B f∵∠3π=A ∴320π<<B ,6566πππ<+<B …………………………………………10分∴1)6sin(21≤+<πB ,23)(1≤<B f∴函数)(B f 的取值范围为]23,1( …………………………………………12分 18.(本小题满分12分) 解:(Ⅰ)依题意得⎪⎩⎪⎨⎧+=+=⨯++⨯+)12()3(5025452233112111d a a d a d a d a …………………………………………2分 解得⎩⎨⎧==231d a , …………………………………………4分1212)1(23)1(1+=+=-+=-+=∴n a n n d n a a n n 即,.……………………………6分(Ⅱ)13-=n nna b ,113)12(3--⋅+=⋅=n n n n n a b …………………………………………7分 123)12(37353-⋅+++⋅+⋅+=n n n T n n n n n T 3)12(3)12(3735333132⋅++⋅-++⋅+⋅+⋅=- ……………………9分n n n n T 3)12(3232323212+-⋅++⋅+⋅+=--nnn n n 323)12(31)31(3231⋅-=+---⋅+=- ∴n n n T 3⋅= …………………………………………12分19.(本小题满分12分)解:(Ⅰ)取AC 中点G,连结FG 、BG , ∵F,G 分别是AD,AC 的中点∴FG ∥CD,且FG=21DC=1 .∵BE ∥CD ∴FG 与BE 平行且相等∴EF ∥BG . ……………………………2分ABC BG ABC EF 面面⊂⊄,∴EF ∥面ABC ……………………………4分 (Ⅱ)∵△ABC 为等边三角形 ∴BG ⊥ACABCDEF G又∵DC ⊥面ABC,BG ⊂面ABC ∴DC ⊥BG ∴BG 垂直于面ADC 的两条相交直线AC,DC ,∴BG ⊥面ADC . …………………………………………6分 ∵EF ∥BG ∴E F ⊥面ADC∵EF ⊂面ADE ,∴面ADE ⊥面ADC . …………………………………………8分 (Ⅲ)连结EC,该四棱锥分为两个三棱锥E -ABC 和E -ADC .43631232313114331=+=⨯⨯+⨯⨯=+=---ACD E ABC E BCDE A V V V .………………………12分 另法:取BC 的中点为O ,连结AO ,则BC AO ⊥,又⊥CD 平面ABC ,∴C CD BC AO CD =⊥ , , ∴⊥AO 平面B C D E ,∴AO 为BCDE A V -的高,43232331,2321)21(,23=⨯⨯=∴=⨯+==-BCDE A BCDE V S AO . 20.(本小题满分12分)解:(Ⅰ)设6组数据的编号分别为1,2,3,4,5,6.设抽到不相邻的两组数据为事件A ,从6组数据中选取2组数据共有15种情况:(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6),其中事件A 包含的基本事件有10种. …………………………………………3分所以321510)(==A P .所以选取的2组数据恰好不相邻的概率是32. ………………………6分(Ⅱ) 当10=x 时,;2|1026219|,262192613910134ˆ<-=+⨯=y ……………………………………9分 当30=x 时,;2|1626379|,263792613930134ˆ<-=+⨯=y所以,该研究所得到的回归方程是可靠的. …………………………………………12分 21.(本小题满分12分)解:(Ⅰ)将1-=x 代入切线方程得2-=y ∴211)1(-=+-=-ab f ,化简得4-=-a b . …………………………………………2分222)1(2)()1()(x xb ax x a x f +⋅+-+=' 12424)(22)1(-===-+=-'bb a b a f . …………………………………………4分解得:2,2-==b a∴122)(2+-=x x x f . …………………………………………6分 (Ⅱ)由已知得122ln 2+-≥x x x 在),1[+∞上恒成立化简得22ln )1(2-≥+x x x即022ln ln 2≥+-+x x x x 在),1[+∞上恒成立 . …………………………………………8分 设22ln ln )(2+-+=x x x x x h ,21ln 2)(-++='xx x x x h ∵1≥x ∴21,0ln 2≥+≥xx x x ,即0)(≥'x h . …………………………………………10分 ∴)(x h 在),1[+∞上单调递增,0)1()(=≥h x h∴)()(x f x g ≥在),1[+∞∈x 上恒成立 . …………………………………………12分22.(本小题满分14分)解(1)设椭圆方程为22221(0)x y a b a b+=>>,12,AF m AF n ==由题意知⎪⎪⎩⎪⎪⎨⎧==+=+6344222m n n m c n m …………………………………………2分解得92=c ,∴39122=-=b .∴椭圆的方程为131222=+y x …………………………………………4分 ∵3=⨯c y A ,∴1=A y ,代入椭圆的方程得22=A x ,将点A 坐标代入得抛物线方程为y x 82=. …………………………………………6分(2)设直线l 的方程为)22(1-=-x k y ,),(),,(2211y x C y x B 由2= 得)22(22212-=-x x ,化简得22221=-x x …………………………………………8分联立直线与抛物线的方程⎪⎩⎪⎨⎧=-=-yx x k y 8)22(12,得0821682=-+-k kx x∴k x 8221=+① …………………………………………10分联立直线与椭圆的方程⎪⎩⎪⎨⎧=+-=-124)22(122y x x k y得0821632)2168()41(2222=--+-++k k x k k x k∴22241821622k kk x +-=+② …………………………………………12分 ∴2222418216)228(222221=++---=-kkk k x x 整理得:0)4121)(2416(2=+--k kk∴42=k ,所以直线l 的斜率为42 . …………………………………………14分。

2013年高考试题及答案一、语文试题(一)文言文阅读1. 阅读下面的文言文,完成下列各题。
(文言文段落省略)(1)下列对文中划线部分的断句,正确的一项是:A. 正确断句B. 错误断句C. 错误断句D. 错误断句(2)下列对文中加点词语的解释,不正确的一项是:A. 解释正确B. 解释不正确C. 解释正确D. 解释正确(二)现代文阅读阅读下面的文章,完成下列各题。
(现代文段落省略)1. 根据文章内容,下列说法不正确的一项是:A. 说法正确B. 说法不正确C. 说法正确D. 说法正确二、数学试题(一)选择题1. 下列哪个选项是正确的数学表达式?A. x + y = zB. 2x - 3y = 5C. 3x^2 + 4y^2 = 9D. 4x^3 - 5y^3 = 102. 如果函数f(x) = ax^2 + bx + c(a ≠ 0)的图像是一个开口向上的抛物线,那么:A. a > 0B. a < 0C. c > 0D. b = 0(二)解答题1. 解方程组:\[\begin{cases}x + y = 5 \\2x - y = 1\end{cases}\]三、英语试题(一)阅读理解阅读下面的短文,然后回答问题。
(短文内容省略)1. What is the main idea of the passage?A. 主旨AB. 主旨BC. 主旨CD. 主旨D(二)完形填空(完形填空段落省略)1. In paragraph 1, the word "astonishing" is closest in meaning to:A. surprisingB. boringC. tiringD. confusing四、综合试题(一)历史1. 下列关于中国历史的叙述,哪一项是错误的?A. 叙述AB. 叙述BC. 叙述C(错误)D. 叙述D(二)地理1. 根据题目所给的地图,确定以下地点的相对位置:A. 地点AB. 地点BC. 地点CD. 地点D五、答案(一)语文答案1. (1)正确断句:A(2)不正确的解释:B2. 不正确的说法:B(二)数学答案1. 正确的数学表达式:B2. 函数图像开口向上的条件:A(三)英语答案1. 主意:C2. 完形填空中“astonishing”的意思:A(四)综合答案1. 历史错误叙述:C2. 地理相对位置:B请注意,以上内容仅为示例,实际的高考试题和答案会根据当年的考试大纲和具体题目而有所不同。

可编辑修改精选全文完整版2013年普通高等学校招生全国统一考试(精校版)全国一卷英语试题第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小脱.从题中所给的A. B.C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What will the couple do soon probably?A.Go to change some clothes.B.Write an essay together.C.Eat out together.2.Whe re are the two speakers probably now?A. In a restaurant.B.At a garage.C. In a hospital.3.Why didn’t the woman drive her car?A. Her car broken down.B. The gas ran out.C. Her car was lent,4.What’s the probabl e relationship between the speakers?A.Colleagues.B.Good friends.C.Boyfriend and girlfriend5.What’s the man’s decision?A. Repairing the typewriter.B. Buying a typewriter.C. Thinking about repairing.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话。
每段对话后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话前,你将有时间阅读各个小题,每小题5秒钟:听完后,各小题给出5秒钟的做答时间。

绝密★启封并使用完毕前2013年普通高等学校招生全国统一考试语文注意事项:1. 本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
第Ⅰ卷1至8页,第Ⅱ卷9至10页。
2. 答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3. 全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束,将本试题和答题卡一并交回。
第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题老子其人其书的时代,自司马迁《史记》以来只有异说,清代学者崇尚考据,对此议论纷纷,如汪中作《老子考异》,力主老子为战国时人,益启争端。
钱穆先生说:“老子伪迹不彰,真相大白,则先秦诸子学术思想之系统条贯始终不明,其源流派别终无可言.”大家都期待这个问题有新的解决线索.过去对于古书真伪及年代的讨论,只能以材料证明纸上材料,没有其它的衡量标准,因而难有定论。
用来印证《老子》的古书,大多收到辨伪家的怀疑,年代确不可移的,恐怕要数到《林非子》。
《吕氏春秋》和《淮南子》,但这几木书戍书太晚,没有多少作用.近年战国秦汉简帛侠籍大黄出上,为学术界提供了许多前所未见的地下材料,这使我们有可能重新考虑《老子》的时代问题。
1973牛长沙马王堆三亏汉基出土的串书,内有《老子》两种版本,甲本字体比较早,不避汉高祖讳,应抄写于高祖即帝位前,乙本避高祖讳,可以抄写于文帝初。
这两本《老子》抄写年代都晚,无益于《老子》著作年代的推定,但乙本前面有《黄帝书》四篇,系。
黄”、“老”合抄之本,则从根本上改变了学术界对早期道家的认识。
郭沐若先生曾指出,道家都是以“发明黄老道德意”为其指归,故也可称之为黄老学派.《老子》和《黄帝书》是道家的经典,在汉初被妙写在《老子》前面的《黄帝书》显然在当时公众心目中已据有崇高位置,不会是刚刚撰就的作品。
同时,《黄帝书》与《申子》、《慎子》、《韩非子》等有许多共通文句,而申不害、慎到、韩非二人均曾学黄老之术,这些共通之处可认作对《皇帝书》的引用阐发。
2013年普通高等学校招生全国统一考试(全国卷)语文试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共6页。
满分150分钟考试结束后,将本试卷和答题卡一并交回。
【注意事项】:1.答题前,考生务必用0.5毫米黑色签字将自己的姓名、座号、考生号、区县和科类填写在答题卡和卡和试卷规定的位置上。
2.第1卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答.答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求怍答的答案无效。
第Ⅰ卷选择题(共30分)一、(12分,每小题3分)1.下列词语中加点的字,读音全都正确的一组是()A.女红.(gōng)安土重.迁移(zhòng)商埠.(fǔ) 花团锦簇.(cù)B.莅.临(lì)大放厥.词(jué)挟.制(xié)蔫.头呆脑(yān)C.懦.弱(nuò)年高德劭.(shāo)两栖.(qī)沁.人心脾(qīn)D.遽.然(jù)精神抖擞.(sǒu)塌.陷(tā)一柱擎.天(qíng)2.下列各句中,加点的成语使用恰当的一项是()A.客厅墙上挂着我们全家在桂林的合影,尽管照片有些褪色,但温馨和美的亲情历历在目....。
B.为了完成在全国的市场布局,我们三年前就行动了,特别是在营销策略的制订上可谓处心积虑....。
C.沉迷网络使小明学习成绩急剧下降,幸亏父母及时发现,并不断求全责备....,他才戒掉了网瘾。
D.他在晚会上出.神入化...的近景魔术表演,不仅令无数观众惊叹不已,还引发了魔术道具的热销。
3.下列各句中,没有语病的一句是()A.波士顿马拉松赛的两声爆炸,无疑给大型体育比赛的安保工作敲响了警钟,如果确保赛事安全,成为组织方必须面对的新难题。
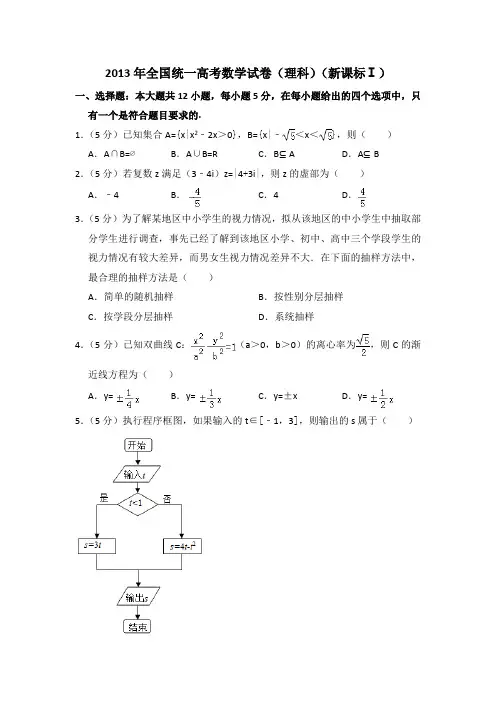
2013·全国卷(文科数学)1. 设全集U ={1,2,3,4,5},集合A ={1,2},则∁U A =( ) A .{1,2} B .{3,4,5} C .{1,2,3,4,5} D .∅1.B [解析] 所求的集合是由全集中不属于集合A 的元素组成的集合,显然是{3,4,5}.2. 已知α是第二象限角,sin α=513,则cos α=( )A .-1213B .-513 C.513 D.12132.A [解析] cos α=-1-sin 2 α=-1213.3. 已知向量=(λ+1,1),=(λ+2,2),若(+)⊥(-),则λ=( ) A .-4 B .-3 C .-2 D .-13.B [解析] (+)⊥(-)⇔(+)·(-)=0⇔=,所以(λ+1)2+12=(λ+2)2+22,解得λ=-3.4. 不等式|x 2-2|<2的解集是( ) A .(-1,1) B .(-2,2)C .(-1,0)∪(0,1)D .(-2,0)∪(0,2)4.D [解析] |x 2-2|<2等价于-2<x 2-2<2,即0<x 2<4,即0<|x |<2,解得-2<x <0或者0<x <2,故所求的不等式的解集是(-2,0)∪(0,2).5. (x +2)8的展开式中x 6的系数是( ) A .28 B .56 C .112 D .2245.C [解析] 含x 6的项是展开式的第三项,其系数为C 28×22=112.6. 函数f (x )=log 2⎝⎛⎭⎫1+1x (x >0)的反函数f -1(x )=( ) A.12x -1(x >0) B.12x -1(x ≠0) C .2x -1(x ∈) D .2x -1(x >0)6.A [解析] 令y =log 2⎝⎛⎭⎫1+1x ,则y >0,且1+1x =2y ,解得x =12y -1,交换x ,y 得f -1(x )=12x-1(x >0). 7. 已知数列{a n }满足3a n +1+a n =0,a 2=-43,则{a n }的前10项和等于( )A .-6(1-3-10) B.19(1-310)C .3(1-3-10) D .3(1+3-10)7.C [解析] 由3a n +1+a n =0,得a n ≠0(否则a 2=0)且a n +1a n =-13,所以数列{a n }是公比为-13的等比数列,代入a 2可得a 1=4,故S 10=4×⎣⎡⎦⎤1-⎝⎛⎭⎫-13101+13=3×⎣⎡⎦⎤1-⎝⎛⎭⎫1310=3(1-3-10).8. 已知F 1(-1,0),F 2(1,0)是椭圆C 的两个焦点,过F 2且垂直于x 轴的直线交C 于A ,B 两点,且|AB |=3,则C 的方程为( )A.x 22+y 2=1B.x 23+y 22=1 C.x 24+y 23=1 D.x 25+y 24=1 8.C [解析] 设椭圆C 的方程为x 2a 2+y 2b 2=1(a >b >0),与直线x =1联立得y =±b 2a (c =1),所以2b 2=3a ,即2(a 2-1)=3a ,2a 2-3a -2=0,a >0,解得a =2(负值舍去),所以b 2=3,故所求椭圆方程为x 24+y 23=1.9. 若函数y =sin(ωx +φ)(ω>0)的部分图像如图1-1所示,则ω=( )图1-1A .5B .4C .3D .29.B [解析] 根据对称性可得π4为已知函数的半个周期,所以2πω=2×π4,解得ω=4.10. 已知曲线y =x 4+ax 2+1在点(-1,a +2)处切线的斜率为8,则a =( )A .9B .6C .-9D .-610.D [解析] y ′=4x 3+2ax ,当x =-1时y ′=8,故8=-4-2a ,解得a =-6.11. 已知正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB ,则CD 与平面BDC 1所成角的正弦值等于( )A.23B.33C.23 D.1311.A [解析] 如图,联结AC ,交BD 于点O .由于BO ⊥OC ,BO ⊥CC 1,可得BO ⊥平面OCC 1,从而平面OCC 1⊥平面BDC 1,过点C 作OC 1的垂线交OC 1于点E ,根据面面垂直的性质定理可得CE ⊥平面BDC 1,∠CDE 即为所求的线面角.设AB =2,则OC =2,OC 1=18=32,所以CE =CC 1·OC OC 1=4 23 2=43,所以sin ∠CDE =CE CD =23.12.、 已知抛物线C :y 2=8x与点M (-2,2),过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若MA →·MB →=0,则k =( )A.12B.22C. 2 D .212.D [解析] 抛物线的焦点坐标为(2,0),设直线l 的方程为x =ty +2,与抛物线方程联立得y 2-8ty -16=0.设A (x 1,y 1),B (x 2,y 2),则y 1y 2=-16,y 1+y 2=8t ,x 1+x 2=t (y 1+y 2)+4=8t 2+4,x 1x 2=t 2y 1y 2+2t (y 1+y 2)+4=-16t 2+16t 2+4=4.MA →·MB →=(x 1+2,y 1-2)·(x 2+2,y 2-2)=x 1x 2+2(x 1+x 2)+4+y 1y 2-2(y 1+y 2)+4 =4+16t 2+8+4-16-16t +4=16t 2-16t +4=4(2t -1)2=0,解得t =12,所以k =1t =2.13. 设f (x )是以2为周期的函数,且当x ∈[1,3)时,f (x )=x -2,则f (-1)=________13.-1 [解析] f (-1)=f (-1+2)=f (1)=1-2=-1. 14.、 从进入决赛的6名选手中决出1名一等奖,2名二等奖,3名三等奖,则可能的决赛结果共有____种.(用数字作答)14.60 [解析] 从6人逐次选出1人,2人,3人分别给奖项即可,方法数为C 16C 25C 33=60.15. 若x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥0,x +3y ≥4,3x +y ≤4,则z =-x +y 的最小值为________.15.0 [解析] 已知不等式组表示区域如图中的三角形ABC 及其内部,目标函数的几何意义是直线y =x +z 在y 轴上的截距,显然在点A 取得最小值,点A (1,1),故z min =-1+1=0.16.、 已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,OK =32,且圆O 与圆K 所在的平面所成的一个二面角为60°,则球O 的表面积等于________.16.16π [解析] 设两圆的公共弦AB 的中点为D ,则KD ⊥DA ,OD ⊥DA ,∠ODK 即为圆O 和圆K 所在平面所成二面角的平面角,所以∠ODK =60°.由于O 为球心,故OK 垂直圆K 所在平面,所以OK ⊥KD .在直角三角形ODK 中,OK OD =sin 60°,即OD =32×23=3,设球的半径为r ,则DO =32r ,所以32r =3,所以r =2,所以球的表面积为4πr 2=16π.17.、 等差数列{a n }中,a 7=4,a 19=2a 9.(1)求{a n }的通项公式;(2)设b n =1na n,求数列{b n }的前n 项和S n .17.解:(1)设等差数列{a n }的公差为d , 则a n =a 1+(n -1)d .因为⎩⎪⎨⎪⎧a 7=4,a 19=2a 9,所以⎩⎪⎨⎪⎧a 1+6d =4,a 1+18d =2(a 1+8d ), 解得a 1=1,d =12.所以{a n }的通项公式为a n =n +12. (2)因为b n =1na n =2n (n +1)=2n -2n +1,所以S n =21-22+22-23+…+2n -2n +1=2n n +1. 18.、 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c )(a -b +c )=ac . (1)求B ; (2)若sin A sin C =3-14,求C . 18.解:(1)因为(a +b +c )(a -b +c )=ac , 所以a 2+c 2-b 2=-ac .由余弦定理得cos B =a 2+c 2-b 22ac =-12,因此B =120°.(2)由(1)知A +C =60°, 所以cos (A -C )=cos A cos C +sin A sin C=cos A cos C -sin A sin C +2sin A sin C =cos(A +C )+2sin A sin C =12+2×3-14 =32, 故A -C =30°或A -C =-30°, 因此C =15°或C =45°. 19.、 如图1-3所示,四棱锥P —ABCD 中,∠ABC =∠BAD =90°,BC =2AD ,△P AB 和△P AD 都是边长为2的等边三角形.图1-3(1)证明:PB ⊥CD ;(2)求点A 到平面PCD 的距离.19.解:(1)证明:取BC 的中点E ,联结DE ,则四边形ABED 为正方形.过P 作PO ⊥平面ABCD ,垂足为O .联结OA ,OB ,OD ,OE .由△P AB 和△P AD 都是等边三角形知P A =PB =PD ,所以OA =OB =OD ,即点O 为正方形ABED 对角线的交点.故OE ⊥BD ,从而PB ⊥OE .因为O 是BD 的中点,E 是BC 的中点,所以OE ∥CD .因此PB ⊥CD .(2)取PD 的中点F ,联结OF ,则OF ∥PB . 由(1)知,PB ⊥CD ,故OF ⊥CD .又OD =12BD =2,OP =PD 2-OD 2=2,故△POD 为等腰三角形,因此OF ⊥PD . 又PD ∩CD =D ,所以OF ⊥平面PCD .因为AE ∥CD ,CD ⊂平面PCD ,AE ⊄平面PCD ,所以AE ∥平面PCD .因此O 到平面PCD 的距离OF 就是A 到平面PCD 的距离,而OF =12PB =1,所以点A 到平面PCD 的距离为1. 20.、、 甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为12,各局比赛的结果相互独立,第1局甲当裁判.(1)求第4局甲当裁判的概率;(2)求前4局中乙恰好当1次裁判的概率.20.解:(1)记A 1表示事件“第2局结果为甲胜”, A 2表示事件“第3局甲参加比赛时,结果为甲负”, A 表示事件“第4局甲当裁判”. 则A =A 1·A 2,P (A )=P (A 1·A 2)=P (A 1)P (A 2)=14.(2)记B 1表示事件“第1局比赛结果为乙胜”,B 2表示事件“第2局乙参加比赛时,结果为乙胜”, B 3表示事件“第3局乙参加比赛时,结果为乙胜”, B 表示事件“前4局中乙恰好当1次裁判”. 则B =B 1·B 3+B 1·B 2·B 3+B 1·B 2, P (B )=P (B 1·B 3+B 1·B 2·B 3+B 1·B 2) =P (B 1·B 3)+P (B 1·B 2·B 3)+P (B 1·B 2)=P (B 1)P (B 3)+P (B 1)P (B 2)P (B 3)+P (B 1)P (B 2) =14+18+14 =58. 21.、 已知函数f (x )=x 3+3ax 2+3x +1.(1)当a =-2时,讨论f (x )的单调性;(2)若x ∈[2,+∞)时,f (x )≥0,求a 的取值范围.21.解:(1)当a =-2时,f (x )=x 3-3 2x 2+3x +1, f ′(x )=3x 2-6 2x +3.令f ′(x )=0,得x 1=2-1,x 2=2+1.当x ∈(-∞,2-1)时,f ′(x )>0,f (x )在(-∞,2-1)上是增函数; 当x ∈(2-1,2+1)时,f ′(x )<0,f (x )在(2-1,2+1)上是减函数; 当x ∈(2+1,+∞)时,f ′(x )>0,f (x )在(2+1,+∞)上是增函数. (2)由f (2)≥0得a ≥-54.当a ≥-54,x ∈(2,+∞)时,f ′(x )=3(x 2+2ax +1)≥3⎝⎛⎭⎫x 2-52x +1=3⎝⎛⎭⎫x -12(x -2)>0, 所以f (x )在(2,+∞)上是增函数,于是当x ∈[2,+∞)时,f (x )≥f (2)≥0. 综上,a 的取值范围是⎣⎡⎭⎫-54,+∞. 22.、、 已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,离心率为3,直线y =2与C 的两个交点间的距离为 6.(1)求a ,b ;(2)设过F 2的直线l 与C 的左、右两支分别交于A ,B 两点,且|AF 1|=|BF 1|,证明:|AF 2|,|AB |,|BF 2|成等比数列.22.解:(1)由题设知ca =3,即a 2+b 2a 2=9,故b 2=8a 2.所以C 的方程为8x 2-y 2=8a 2. 将y =2代入上式,并求得x =±a 2+12.由题设知,2a 2+12=6,解得a 2=1.所以a =1,b =2 2.(2)证明:由(1)知,F 1(-3,0),F 2(3,0),C 的方程为8x 2-y 2=8.①由题意可设l 的方程为y =k (x -3),|k |<22,代入①并化简得(k 2-8)x 2-6k 2x +9k 2+8=0.设A (x 1,y 1),B (x 2,y 2),则x 1≤-1,x 2≥1,x 1+x 2=6k 2k 2-8,x 1x 2=9k 2+8k 2-8.于是|AF 1|=(x 1+3)2+y 21=(x 1+3)2+8x 21-8=-(3x 1+1),|BF 1|=(x 2+3)2+y 22=(x 2+3)2+8x 22-8=3x 2+1.由|AF 1|=|BF 1|得-(3x 1+1)=3x 2+1,即x 1+x 2=-23.故6k 2k 2-8=-23,解得k 2=45,从而x 1x 2=-199.由于|AF 2|=(x 1-3)2+y 21=(x 1-3)2+8x 21-8=1-3x 1,|BF 2|=(x 2-3)2+y 22=(x 2-3)2+8x 22-8=3x 2-1,故|AB |=|AF 2|-|BF 2|=2-3(x 1+x 2)=4, |AF 2|·|BF 2|=3(x 1+x 2)-9x 1x 2-1=16. 因而|AF 2|·|BF 2|=|AB |2,所以|AF 2|,|AB |,|BF 2|成等比数列.。
2013年全国统一高考历史试卷(新课标Ⅰ)一、选择题(4×12分)1.(4分)在周代分封制下,墓葬有严格的等级规定。
考古显示,战国时期,秦国地区君王墓葬规模宏大,其余墓葬无明显等级差别;在经济发达的东方六国地区,君王、卿大夫、士的墓葬等级差别明显。
这表明( )A.经济发展是分封制度得以维系的关键B.分封制中的等级规定凸显了君主集权C.秦国率先消除分封体制走向集权统治D.东方六国仍严格遵行西周的分封制度2.(4分)自汉至唐,儒学被奉为“周(公)孔之道”,宋代以后儒学多被称作“孔孟之道”,促成这一变化的是( )A.宗法血缘制度逐渐瓦解B.仁政理念深入人心C.程朱理学成为统治思想D.陆王心学日益兴起3.(4分)有学者说,在古代雅典,“政治领袖和演说家根本就是同义语”。
这一现象是雅典( )A.政治体制的产物B.社会矛盾缓和的反映C.频繁改革的结果D.思想文化繁荣的体现4.(4分)1688年,英国议会迎立荷兰执政威廉为国王,并拥立他的妻子玛丽(詹姆士二世的女儿)为女王,目的是( )A.加强英国与荷兰的友好关系B.否定王位世袭男性优先原则C.通过双王相互牵制防止独裁D.为光荣革命披上合法的外衣5.(4分)恩格斯称赞一位近代科学家的研究成就是“自然科学的独立宣言”,他指的应是( )A.哥白尼的“日心说”否定了宗教神学崇信的“地心说”B.伽利略创立的实验科学推动了近代科学的发展C.牛顿创立经典力学完成了科学史上的划时代飞跃D.达尔文的生物进化论颠覆了关于人类起源的传统观念6.(4分)现代化是晚清历史发展的一个趋向,最能体现这一趋向的是( )A.洋务运动﹣戊戌政变﹣清末新政B.洋务运动﹣戊戌变法﹣辛亥革命C.鸦片战争﹣中法战争﹣甲午战争D.太平天国运动﹣义和团运动﹣辛亥革命7.(4分)1928年中共六大通过的《政治议决案》指出:各省自发的农民游击战争,只有和“无产阶级的城市的新的革命高潮相联结起来”,才可能变成“全国胜利的民众暴动的出发点”。
2013年普通高等学校招生全国统一考试(湖南卷)英语PartⅠListening Comprehen s ion (30 marks) Section A(22.5 marks)will hear six conversations between two speakers. For each this se se c tion, y o u u will Directions: In this conversation, there are several questions and each question is followed by three choices marked A, B and C. Listen carefully and then choose the best answer for each question. You will hear each conversation TWICE. Conversation 1 1. Where is the man going? A. Kennedy. B. London. C. New York. 2. When should the man arrive at the airport? A. By 8:15. B. By 9:00. C. By 9:25. Conversation 2 3. What is the woman doing? A. Taking a taxi. B. Doing shopping. C. Waiting for the man. 4. Where are the two speakers going to meet? A. At home. B. In a shop. C. In a restaurant. Conversation 3 5. What is the woman looking for? A. A pan. B. Carrots. C. Tomatoes. 6. What will the speakers probably have tonight? A. French fries. B. Noodles. C. Fried chicken. Conversation 4 7. What will the project focus on? A. A dog. B. A fish. C. A cat. 8. What can we know about John? A. He has conducted the survey. B. He is making cards now. C. He will do the introduction. 9. Who can handle the summarizing? A. Carol. B. Tom. C. Mary. Conversation 5 ‟s vacation? 10. What can we know about the womanA. She will stay on the beaches. B. She will go camping in the jungle. C. She will spend 3 weeks in South Africa. 11. Which does the woman need to bring? A. A map. B. A tent. C. Some clothes. 12. Who will prepare the meals? A. The man. B. The guide. C. The woman. Conversation 6 13. What are the two speakers doing? A. Discussing a lecture. B. Visiting a museum. C. Attending a party. 14. Which job has Jane applied for? A. Salesgirl. B. Waitress. C. V olunteer. 15. What is the probable relationship between the two speakers? A. Teacher and student. B. Father and daughter. C. Classmates. Section B (7.5 marks)Directions: In this section, you will hear a short passage. Listen carefully and then fill in the numbered blanks with the information you have heard. Fill in each blank with NO MORE THAN THREE WORDS. You will hear the short passage TWICE.Part II Language Knowledge (45 marks) Section A(15 marks) Directions: For each of the following unfinished sentences there are four choices marked A, B, C and D. Choose the one that best completes the sentence.21. Happiness and success often come to those ________ are good at recognizing their own strengths. A. whom B. who C. what D. which 22. “What do you want to be?” asked Mrs. Crawford. “Oh, I ________ president,” said the boy, with a smile. A. have been B. am C. was D. will be 23. You must learn to consult your feelings and your reason ________ you reach any decision. A. although B. before C. because D. unless 24. Around two o ‟clock every night, Sue will start talking in her dream. It somewhat ________ us. A. bothers B. had bothered C. would bother D. bothered 25. The sun began to rise in the sky, ________ the mountain in golden light. A. bathed B. bathing C. to have bathed D. have bathed 26. If nothing ________, the oceans will turn into fish deserts. A. does B. had been done C. will do D. is done 27. — Have you heard about the recent election? — Sure, it ________ the only thing on the news for the last three days. A. would be B. is C. has been D. will be 28. Do not let any failures discourage you, for you can never tell ________ close you may be to victory. A. how B. that C. which D. where How to Speak English 16. ___________I. Speak oftenThe more often you speak, the 17. ___________ it becomes II. Relax & 18. ___________ the message● Don‟t focus on the grammar rules only. ● Talk about something 19. ___________. III. Practise what you want to saySpeak to 20. ___________ a few times. 29. You cannot accept an opinion ________ to you unless it is based on facts. A. offering B. to offer C. having offered D. offered 30. Every day ________ a proverb aloud several times until you have it memorized. A. read B. reading C. to read D. reads 31. ________ warm at night, I would fill the woodstove, then set my alarm clock for midnight so I could refill it. A. Staying B. Stayed C. To stay D. Stay 32. He ________ sleep, although he tried to, when he got on such a hunt for an idea until he had caught it. A. wouldn‟t B. shouldn ‟t C. couldn ‟t D. mustn ‟t 33. The university estimates that living expenses for international students ________ around $8,450 a year, which ________ a burden for some of them. A. are ;is B. are ;are C. is ;are D. is ;is 34. — I don ‟t understand why you didn ‟t go to the lecture yesterday afternoon. — had done B. was doing C. would do D. am doing 35. Not once ________ to Michael that he could one day become a top student in his class. A. occurred it B. it did occur C. it occurred D. did it occur Section B (18 marks)Directions: For each blank in the following passage there are four words or phrases marked A, B, C and D. Fill in each blank with the word or phrase that best fits the context.When I was 8 years old, I once decided to run away from home. With my suitcase 36 and some sandwiches in a bag, I started for the front door and said to Mom, “I ‟m leaving.”“If you want to 37 , that‟s all right,” she said. “But you came into this home without anything and you can leave the same way.” I 38 my suitcase and sandwiches on the floor heavily and started for the door again. “Wait a minute,” Mom said. “I want your 39 back. You didn‟t wear anything when you arrived.” This This really really really angered angered angered me. me. me. I I I tore tore tore my my my clothes clothes clothes off off off——shoes, shoes, socks, socks, socks, underwear underwear underwear and and and all all all——and 40 , , ““Can Can I I I go go now?now?””“Y es,” Mom answered, “but once you close that door, don ‟t expect to come back.” I I was was was so so 41 that that I I I slammed slammed slammed ((砰地关上) ) the door the door and stepped stepped out out out on on on the the the front front front porch. porch. 42 I realized realized that that that I I I was was was outside, outside, outside, with with with nothing nothing nothing on. Then on. Then I I noticed noticed noticed that that that down down down the the the street, street, street, two two two neighbor girls neighbor girls were walking toward our house. I ran to 43 behind a big tree in our yard at once. After a while, I was 44 the girls had passed by. I dashed to the front door and banged on it loudly. “Who Who‟‟s there?” I heard. “It It‟‟s Billy! Let me in!” The voice behind the 45 answered, “Billy doesn‟t live here anymore. He ran away from home.” Glancing behind me to see if anyone else was coming, I begged, “w, c A w, c‟‟mon, Mom! I ‟m 46 your son. Let me in!”The door inched open and Mom ‟s smiling face appeared. “Did you change your 47 about running away?away?”” she asked. “What What‟‟s for supper?” I answered. (277 words)36. A. packed B. returned C. cleaned D. repaired 37. A. drop out B. go by C. move around D. run away 38. A. pressed B. shook C. threw D. pulled 39. A. bag B. clothes C. sandwiches D. suitcase 40. A. explained B. suggested C. continued D. shouted 41. A. angry B. sorry C. frightened D. ashamed 42. A. Certainly B. Naturally C. Suddenly D. Possibly 43. A. play B. bide C. rest D. wave 44. A. sure B. proud C. eager D. curious 45. A. house B. tree C. door D. yard 46. A. also B. still C. even D. already 47. A. conclusion B. promise C. concern D. decision Section C (12 marks)Directions: Complete the following passage by filling in each blank with one word that best fits the context.When kids in parts of the world want to play, they often make soccer balls out of trash tied together with string. “ 48 the areas used for playing fields are often rough and rocky, millions of real balls go flat (变瘪) 49 24 24 hours,hours,hours,”” says says Tim Tim Tim Jahnigen, Jahnigen, Jahnigen, a a a California California California businessman. businessman. businessman. Determined Determined Determined to to to solve solve solve this this this problem, problem, 50 created an indestructible ball called the One World Futbol. The ball is made of 51 special material, e thylene-vinyl ethylene-vinyl acetate foam . It ‟s lightweight, it ‟s flexible, and and—— 52 important important——it holds its shape. The One World Futbol needs no pump 53 won won‟‟t wear out, even on rough surfaces. When tested, 54 withstood (经受住经受住) being crushed by a car, and even being chewed on by a lion. Although Although it it it costs costs costs more more more to to to produce produce 55 a a typical typical typical soccer soccer soccer ball, ball, ball, Jahnigen Jahnigen Jahnigen estimates estimates estimates the the the One One One World World Futbol can last 30 years. So far, it ‟s been given to kids in 143 countries. (154 words)Part III Reading Comprehension (30 marks)Directions: Read the following three passages. Each passage is followed by several questions orunfinished statements. For each of them there are four choices marked A, B, C and D. Choose the one that fits best according to the information given in the passage.APlanning a visit to the UK? Here we help with ways to cut your costs. A VOID BIG EVENTS Big Big sporting sporting sporting events, events, events, concerts concerts concerts and and and exhibitions exhibitions exhibitions can can can increase increase increase the the the cost cost cost of of accommodation and make it harder to find a room. A standard double room at the Thistle Brighton on the final Friday of the Brighton Comedy Festival (19 Oct.) cost £169.15 at . A week later, the same room cost £118.15. 118.15. If you can be flexible and want to know dates to avoid —or you ‟re looking for a big event to pass your time time——check out sites such as , which allow you to search for events in the UK by city, date and category. STAYAWSTAYAWAY AY FROM THE STATION If traveling to your destination by train, you may want to find a If traveling to your destination by train, you may want to find a good base close to the station, but you could end up paying more for the sake of convenience at the start of your holiday. Don Don‟‟t be too choosy about the part of town you stay in. Booking two months in advance, the cheapest room at Travelodge ‟s Central Euston hotel in London for Saturday 22 September was £95.95. A room just a tube journey away at its Covent Garden hotel was £75.75. And at Farringdon, a double room cost just £62.95. LOOK AFTER YOURSELF Really central hotels in cities such as London, Edinburgh and Cardiff can cost cost a a a fortune, fortune, fortune, especially especially especially at at at weekends weekends weekends and and and during during during big big big events. events. events. As As As an an an alternative alternative alternative consider consider consider checking checking checking into into into a a self-catering self-catering flat flat flat with with with its its its own own own kitchen. kitchen. kitchen. Often Often Often these these these flats flats flats are are are hidden hidden hidden away away away on on on the the the top top top floors floors floors of of of city city city centre centre buildings. A great example is the historic O ‟Neill Flat on Edinburgh ‟s Royal Mile, available for £420 for five days in late September, with room for four adults. GET ON A BIKE London London ‟s …Boris bikes ‟ have attracted the most attention, but other cities also have similar programmes that let you rent a bicycle and explore at your own pace, saving you on public transport or car parking costs. Among the smaller cities with their own programmes are Newcastle (casual members pay around £1.50 for two hours) and Cardiff (free for up to 30 minutes, or £5 per day). (358 words)56. The Brighton Comedy Festival is mentioned mainly to show big events may __________. A. help travelers pass time B. attract lots of travelers to the UK C. allow travelers to make flexible plans D. cause travelers to pay more for accommodation 57. “Farringdon Farringdon”” in Paragraph 5 is most probably __________. A. a hotel away from the train station B. the tube line to Covent Garden C. an ideal holiday destination D. the name of a travel agency 58. The passage shows that the O ‟Neill Flat __________. A. lies on the ground floor B. is located in central London C. provides cooking facilities for tourists D. costs over £100 on average per day in late September 59. Cardiff ‟s program allows a free bike for a maximum period of __________. A. half an hour B. one hour C. one hour and a half D. two hours 60. The main purpose of the passage is __________. A. to tell visitors how to book in advance B. to supply visitors with hotel information C. to show visitors the importance of self-help D. to offer visitors some money-saving tips BIn my living room, there is a plaque (匾) that advises me to “Bloom (开花开花) where you are planted.” It reminds reminds me me me of of of Dorothy. Dorothy. Dorothy. I I I got got to to know know know Dorothy Dorothy Dorothy in in in the the the early early early 1980s, 1980s, 1980s, when when when I I I was was was teaching teaching teaching Early Early Early Childhood Childhood Development Development through through through a a a program program program with with with Union Union Union College College College in in in Barbourville, Barbourville, Barbourville, Kentucky. Kentucky. Kentucky. The The The job job job responsibilities responsibilities required occasional visits to the classroom of each teacher in the program. Dorothy stands out in my memory as one who “bloomed bloomed”” in her remote area. Dorothy Dorothy taught taught taught in in in a a a school school school In In In Harlan Harlan Harlan County, County, County, Kentucky, Kentucky, Kentucky, Appalachian Appalachian Appalachian Mountain Mountain Mountain area. area. area. To To To get get get to to to her her school from the town of Harlan, I followed a road winding around the mountain. In the eight-mile journey, I crossed the same railroad track five times, giving the possibility of getting caught by the same train five times. Rather than feeling excited by this drive through the mountains, I found it depressing. The poverty level was shocking and the small shabby houses gave me the greatest feeling of hopelessness. From From the the the moment moment moment of of of my my my arrival arrival arrival at at at the the the little little little school, school, school, all all all gloom gloom gloom ((忧郁) ) disappeared. disappeared. disappeared. Upon Upon Upon arriving arriving arriving at at Dorothy Dorothy‟‟s s classroom. classroom. classroom. I I I was was was greeted greeted greeted with with with smiling smiling smiling faces faces faces and and and treated treated treated like like like a a a queen. queen. queen. The The The children children children had had had been been prepared prepared to to to show show show me me me their their their latest latest latest projects. projects. projects. Dorothy Dorothy Dorothy told told told me me me with with with a a a big big big smile smile smile that that that they they they were were were serving serving serving poke poke greens salad and cornbread for “dinner dinner”” (lunch). In case you don ‟t know, poke greens are a weed-type plant that grows wild, especially on poor ground. Dorothy Dorothy never never never ran ran ran out out out of of of reports reports reports of of of exciting exciting exciting activities activities activities of of of her her her students. students. students. Her Her Her enthusiasm enthusiasm enthusiasm never never never cooled cooled down. When it came time to sit for the testing and interviewing required to receive her Child Development Associate Certification, Dorothy was ready. She came to the assessment and passed in all areas. Afterward, she invited me to the one-and-only steak house in the area to celebrate her victory, as if she had received her Ph. D. degree. After the meal, she placed a little box containing an old pen in my hand. She said it was a family heirloom (传家宝), but to me it is a treasured symbol of appreciation and pride that cannot be matched with things. (360 words) 61. “Early Childhood Development ” in Paragraph 1 refers to __________. A. a program directed by Dorothy B. a course given by the author C. an activity held by the students D. an organization sponsored by Union college 62. In the journey, the author was most disappointed at seeing __________. A. the long track B. the poor houses C. the same train D. the winding road 63. Upon arriving at the classroom, the author was cheered up by __________. A. a warm welcome B. the sight of poke greens C. Dorothy‟s latest projects D. a big dinner made for her 64. What can we know about Dorothy from the last paragraph? A. She was invited to a celebration at a restaurant. B. She got a pen as a gift from the author. C. She passed the required assessment. D. She received her Ph. D. degree. 65. What does the author mainly intend to tell us? A. Whatever you do, you must do it carefully. B. Whoever you are, you deserve equal treatment. C. However poor you are, you have the right to education, D. Wherever you are, you can accomplish your achievement. CIt It‟‟s such a happy-looking library, painted yellow, decorated with palm-tree stickers and sheltered from the Florida sun by its own roof. About the size of a microwave oven, it ‟s pedestrian-friendly, too, waiting for book lovers next to a sidewalk in Palm Beach country Estates, along the northern boundary of Palm Beach Gardens. It It‟‟s a library built with love. A A year year year ago, ago, ago, shortly shortly shortly after after after Janey Janey Janey Henriksen Henriksen Henriksen saw saw saw a a a Brian Brian Brian Williams Williams Williams report report report about about about the the the Little Little Little Free Free Free Library Library organization, a Wisconsin-based nonprofit that aims to promote literacy and build a sense of community in a neighborhood neighborhood by by by making making making books books books freely freely freely available, available, available, she she she announced announced announced to to to her her her family family family of of of four, four, four, ““That That‟‟s what what we we we‟‟re going to do for our spring break!”Son Austin, now a 10th-grader, didn‟t see the point of building a library that resembles a mailbox. But Janey insisted, and husband Peter unwillingly got to work. The 51-year-old owner of a ship supply company modified a small wooden house that he ‟d built years earlier for daughter Abbie ‟s toy horses, and made a door of glass. After After adding adding adding the the the library library library‟‟s s final final final touches touches touches ((装点), ), the the the family family family hung hung hung a a a signboard signboard signboard on on on the the the front, front, front, instructing instructing users to “take a book, return a book,” and making the Henriksen library, now one of several hundred like it nationwide and among more than 2,500 in the world, the only Little Free Library in Palm Beach County. They stocked it with 20 or so books they‟d already read, a mix of science fiction, reference titles, novels and kids ‟ favorites. “I told them, keep in mind that you might not see it again,” said Janey, a stay-at-home mom. Since then, the collection keeps replenishing (补充) itself, thanks to ongoing donations from borrowers. The library now gets an average of five visits a day. The The projectproject project‟‟s s best best best payoff, payoff, payoff, says says says Peter, Peter, Peter, are are are the the the thank-you thank-you thank-you notes notes notes left left left behind. behind. behind. ““e W e had had had no no no idea idea idea in in in the the beginning that it would be so popular.” (317 words) 66. In what way is the library “pedestrian-friendly pedestrian-friendly””? A. It owns a yellow roof. B. It stands near a sidewalk. C. It protects book lovers from the sun. D. It uses palm-tree stickers as decorations. 67. Janey got the idea to build a library from __________. A. a visit to Brian Williams B. a spring break with her family C. a book sent by one of her neighbors D. a report on a Wisconsin-based organization 68. The library was built __________. A. by a ship supply company B. on the basis of toy horses C. like a mailbox D. with glass 69. What can we infer about the signboard? A. It was made by a user of the library. B. It marked a final touch to the library. C. It aimed at making the library last long. D. It indicated the library was a family property. 70. The passage tells us that the users __________. A. donate books to the library B. get paid to collect books for the library C. receive thank-you notes for using the library D. visit the library over 5 times on average daily Part IV Writing (45 marks)Section A (10 marks)Directions: Read the following passage. Fill in the numbered blanks by using the information from the passage.Write NO MORE THAN THREE WORDS for each answer.While there is no widely accepted definition of MOOCs, their key features are open access :they are currently currently free free free to to to participants, participants, participants, no no no entry entry entry qualifications qualifications qualifications are are are required, required, required, they they they support support support an an an unlimited unlimited unlimited number number number of of participants and as yet, very few include any form of accreditation (认证). Currently offered by some famous universities, MOOCs are attractive to people who do not have the financial financial resources resources resources to to to meet meet meet the the the growing growing growing costs costs costs of of of university university university education, education, or or who who who do do do not not not have have have formal formal qualifications. They also allow participants to study at their own pace. The potential for MOOCs to deliver education is obviously vast—they could be considered as a huge step step forwards forwards forwards in in in widening widening widening participation. participation. participation. They They They also also also have have have the the the potential potential potential to to to provide provide provide a a a unique unique unique window window window on on universities that offer popular and valuable courses, they may attract some participants to register for formal fee-paying fee-paying programmes programmes programmes at at at the the the same same same or or or other other other universities universities universities and and and are are are likely likely likely to to to promote promote promote new new new ways ways ways of of of on-line on-line education. However, it is still very early days for MOOCs. The quality of the education provision is highly variable, with many courses offering only recordings of lectures, and delivery is particularly difficult in some special fields that require practical classes, research projects or extensive library access. Besides, wider engagement with participants requires very considerable resource. Even limited feedback or examination becomes a major task if there are several thousand students in the class. Considering the challenges, some people argue MOOCs will soon evaporate (蒸发). But they certainly provide good opportunity for widening higher education, are a means of raising awareness of universities to audiences of tens or hundreds of thousands, and are well worthy of serious consideration. (271 words) Section B (10 marks)Directions: Read the following passage. Answer the questions according to the information given in the passage.“Let ’s Talk ”:The Free Advice ProjectA A few few few weeks weeks weeks ago, ago, ago, I I I took took took a a a walk walk walk around around around Washington Washington Washington Square Square Square Park. Park. Park. I I I met met met all all all the the the usual usual usual people people :street performers, the Pigeon Guy, a group of guitarists singing in harmony. But off to the side, sitting on a bench was a woman doing something vastly different —giving free advice. A week or two later, I set up an interview with her and we discussed her project at length. ● free participation at present ● 72. _________ for entry qualifications ● support of countless participants ● rare inclusion of accreditation ● being attractive to people » who 73. _________ university education or » who have 74. _________ ● being flexible in the study pace ● widening participation significantly ● 76. _________ a unique window on universities ● attracting students to register for formal progarmmes ● promoting on-line education Key features Attractions 75. _________ 77. _________ ● highly variable quality of the education provision ● 78. _________ of some special courses ● demand for very considerable resource The future● uncertainty » possibly 79._________ ● certainty » widening higher education » raising awareness of universities » being well worth 80. _________ seriously Title : 71. _____ Lisa Podell, 32, started the Free Advice Project this past May. It began as an experiment ;she sat in Washington Square Park for a day with a sign that read “Free Advice ” as a simple way to reach out to people. Podell was astonished at the strong response. Podell Podell admits admits admits that that that she she she was was was doubtful doubtful doubtful at at at first, first, first, but but but now now now she she she describes describes describes the the the project project project as as as mutually mutually mutually ((相互地) beneficial. People learn from her —but she also learns from them. She says that the majority of those who come to her are dealing with some pretty heavy issues, and they expect her not only to listen, but also provide real answers. Having Having worked worked worked as as as a a a full full full time time time teacher teacher teacher and and and now now now as as as an an an adolescent adolescent adolescent advisor, advisor, advisor, Podell Podell Podell believes believes believes that that that talking talking things out is an important in the decision-making process. Sometimes, people walk around all day, keeping their problems in their own head and thinking about them in the same way. Podell simply strives to provide people with perspective. I asked if there is a future plan for the Free Advice Project. Podell said she would like to promote it to each public space in New York, which would be carried out by various volunteers across the city. It It was was was truly truly truly inspiring inspiring inspiring to to to meet meet meet someone someone someone with with with such such such a a a big big big heart, heart, heart, especially especially especially in in in New New New Y Y ork —where where it it it is is sometimes very hard to find anybody to listen. (303 words)81. In what way was Podell different from other people in the park? (No more than 6 words) (2 marks) ___________________________________________________________________________________ 82. What do people in need expect Podell to do? (No more than 10 words) (3 marks) ___________________________________________________________________________________ 83. According to Podell, what should people do when making decisions? (No more than 6 words) (2 marks) ___________________________________________________________________________________ 84. How would Podell promote her project in New York? (No more than 15 words) (3 marks) ___________________________________________________________________________________ Section C (25 (25 marks)Directions: Write an English composition according to the instructions given below. 请以下列词语为关键词写一篇英语短文。
1.2013年普通高等学校招生全国统一考试英语(课标卷I)选择题答案第一、二、三部分36-40 CCDAB41-45 DABAC 46-50 CDDBA 51-55 BCADB 56-60 AACCB61-65 DCDDB 66-70 BCABD第二节:One Possible VersionDear Peter,How are you doing?I’m writing to tell you that my uncle Li Ming is going to your city for a conference, and I’ve asked him to bring you the Chinese painting you’ve asked for before.Also, I’d like you to do me a favor. Would you please meet my uncle at the airport and take him to his hotel since this is his first visit to the U.S.? Thank you in advance!His flight number is CA985, and it will arrive at 11:30 am, August 6. My uncle is tall and he is wearing glasses. And he will be in a blue jacket.Looking forward to your reply.Yours,Li Hua2.2013年普通高等学校招生全国统一考试英语(课标卷II)选择题:16-20: ADBBA 21-25: CBDCA 26-30: CDBCA31-35: DDBCA 36-40: BADBA 41-45: DBDCD 46-50: CABCDDear Tom,How are you doing? I wonder if you could sell some Chinese knots for me. I made them myself with red silk threads, cloth and other materials. They look really beautiful in the shape of a diamond, about 5 inches long and 4 inches wide. In china, these knots stand for friendship, love and good luck. People can either give them as gifts to friends or hang them in their houses. They are only 12.99 US dollars each. If anyone wants to know more about the knots, let them write to me. Also, do let me know if you need further information. Thank you!Li hua.2013年普通高等学校招生全国统一考试英语(大纲卷)选择题答案:第一、二、三部分:1.A 2.C 3.A 4.C 5.B 6.B 7.B 8.A 9.B 10.A11.B 12.A 13.C 14.A 15.A 16.B 17.C 18.B 19.C 20.C21.D 22.A 23.A 24.C 25.D 26.B 27.C 28.A 29.B 30.B31.D 32.B 33.A 34.D 35.C 36.A 37.D 38.B 39.B 40.A41.C 42.B 43.D 44.C 45.A 46.C 47.D 48.B 49.C 50.A51.D 52.D 53.B 54.C 55.A 56.B 57.A 58.D 59.B 60.A61.D 62.B 63.D 64.C 65.D 66.C 67.A 68.B 69.A 70.C71.D 72.C 73.A 74.C 75.B非选择题答案:第二节:英语答案第1页(共2页)Dear Tom,How are you doing? I wonder if you could sell some Chinese knots for me. I made them myself with red silk threads, cloth and other materials. They look really beautiful in the shape of a diamond, about 5 inches long and 4 inches wide. In china, these knots stand for friendship, love and good luck. People can either give them as gifts to friends or hang them in their houses. They are only 12.99 US dollars each. If anyone wants to know more about the knots, let them write to me. Also, do let me know if you need further information. Thank you!Li hua.4. 2013年普通高等学校招生全国统一考试英语(北京卷)第二部分: 第一节:单选21-25: DACBB 25-30: CDBDA 31-35: BCCDA第二节: 完形36-40: CAADB 41-45:BCDCD46-50:ACBDA 51-55:BDCAB第三部分: 阅读56-60: BADAC 61-65: CDBBA 66-70:DDACC 71-75: EDBAF第四部分:作文第一节:情景作文内容要点:1. 告别2.生病3.照顾. 4.夸奖Last Monday, my father said goodbye to my mother and me and went on a business trip. He would be awayfor three days. Just the next morning, I found my mother wasn’t feeling well. She had a cold. I immediatelywent to get her some medicine and then prepared some noodles for her, with my special care. My mother recovered quickly. When my father came back home, my mother told him what had happened he praised me for what I had done. I feel very happy that I have done something for my mother第二节开放作文I think the picture is telling us that there is usually a difference between one’s dream and reality. Peopleneed to learn to face it. Everyone has his dream, however, it is not so easy for people to realize their dreamsevery time. Just like the man in the picture, instead of the big fish he wishes for. He actually catches a smallone. In my opinion, People need to learn to accept the reality and keep on trying. With another try, they may gain what they dream of.5. 2013年普通高等学校招生全国统一考试英语(天津卷)单选1-15 BABDC BCAAD ACDBD完形16-35 CDABA BCDBA CDCBA ABACD阅读36-55 ABCDD ACDBC BCBDA ACDBDGood afternoon, my dear friends,My name is Li Jin. I feel excited to have the honor of running for vice president of our English Club. I think I am fully qualified for the job.Firstly, I am easygoing and can communicate with others in English fluently. Secondly, as a dynamic person, I have rich experience in organizing activities, such as English parties and all kinds of lectures. I will make good plans and spare no efforts to do more exchanges with other schools by holding English Speech Competition and debates if I get the chance. If I am lucky enough to be elected, I will make great contributions to serve students and try to make their life more colorful! I sincerely hope you can give me a chance. Thank you!6.2013年普通高等学校招生全国统一考试英语(上海卷)第一大题第1至第10小题,每题1分;第11至第16小题,每题2分;第17至第24小题,每题1分,共30分。
2013年普通高等学校招生全国统一考试(福建卷)英语试题第I卷(选择题共115分)第一部分听力(共两节,满分30分)第一节1. What does the man want to do?A. Take photos.B. Buy a camera.C. Help the woman.2. What are the speakers talking about?A. A noisy night.B. Their life in town.C. A place of living.3. Where is the man now?A. On his way.B. In a restaurant.C. At home.4. What will Celia do?A. Find a player.B. Watch a game.C. Play basketball.5. What day is it when the conversation takes place?A. Saturday.B. Sunday.C. Monday.笫二节(共15小题;每小题1.5分,满分22.5分)听第6段材料,回答第6、7题。
6. What is Sara going to do?A. Buy John a gift.B. Give John a surprise.C. Invite John to France.7. What does the man think of Sara's plan?A. Funny.B. Exciting.C. Strange.听第7段材料,回答第8、9题。
8. Why does Diana say sorry to Peter?A. She has to give up her travel plan.B. She wants to visit another city.C. She needs to put off her test.9. What does Diana want Peter to do?A. Help her with her study.B. Take a book to her friend.C. Teach a geography lesson.听第8段材料,回答第10至12题。
浙江省2013年度《全国建设工程造价员资格》考试试卷
建筑工程计价试题(闭卷)
一、单项选择题(15题,每题1分,共15分。
将正确答案选项的编号填入答题卡相应位置。
选对得分,不选、选错均不得分。
题中中未作说明的工料机价格均以2010版定额本为准。
)
1、下列说法中不正确的是
A、本定额中所使用的砂浆是按普通砂浆和预拌砂浆考虑的
B、本定额中的混凝土构件浇捣,制作未包括添加剂
C、定额中的人工消耗置包括了直接用工、其他用工及人工幅度差
D、定额中遇有两个或两个以上系数时,按连乘法计算
2、内的室内楼梯间和各类并道的建筑面积,应按所依附的速筑物的( )计算.并入建筑钧的建筑面积内.
A、结构层
B、自然层
C、单层空间
D、多层空间
3、挖土方的工程量按设计图示尺寸以体积计算,此处的土方体积是指(
A、虚方体积
B、夯实后体积
C、松填体积
D、天然密实体积
4、下列关于桩长的说法正确的是()。
A、计算预制钢筋混凝土方桩工程量时,桩长不包括桩尖
B、计算预应力钢筋混凝土管桩工程量时.桩长包括桩尖
C、沉管灌注桩的设计桩长包括预制桩尖
D、人工挖孔桩的孔深按打桩前的自然地坪标高至设计桩底标高的长度计算
5、在砖混结构中,浇注构造柱和砌砖墙的工序是()。
A、先浇后砌
B、先砌后浇
C、同时进行
D、不分先
6、下列关于防水工程计量规则说法错误的是()。
A、设计无规定时,伸缩缝的弯起部分按250mm计.
B、设计无规定时,天窗的弯起部分按250mm计
C、平面与立面连接处高度在500mm以内的立面面积并入平面防水面积计算
D、涂抹防水按露面面实铺面积计算
7、下列项目中,不是以平方米为单位计算的是()。
A、泡沫玻璃 B.膨胀珍珠岩板
C、聚氨酯硬泡(喷涂)
D、硬泡聚氨酯保温板
8、块料镶贴和装饰抹灰的“零星项目不适用于()。
A、挑檐
B、天沟 C.雨蓬底面 D、扶手
9、附墙柱的侧面抹灰()。
A、计算墙面抹灰工程量时不计算
B、执行柱抹灰定额
C、计算柱面抹灰工程量时不予增加
D、并入相应墙面抹灰工程量计算
10、关于门窗工程中的工程量计算规则,下列说法中正确的为()。
A、门窗均按框外围面积计算
B、普通木门窗均按设计洞口面积计算
C、弧形门窗和无框玻璃门按展开面积计算
D、门窗均按设计图示尺寸以展开面积计算
11、天朋工程中有关工程量的计算.不正确的说法是()。
A、天棚吊顶不分跌级与平面,基层与饰面板均按设计图示尺寸以展开面积计算
B、天棚吊顶面层应扣除0.3m2以外的独立柱所占面积
C、夹板天棚面层应扣除灯孔所占面积
D、灯槽按展开面积以“m2”计算
12、油漆工程中不以展开面积计算工程量的构件为()
A、钢屋架
B、H型钢梁、吊车梁
C、钢爬梯
D、钢管柱
13、美术字安装,按宇的()以个计算。
A、实际面积
B、展开面积
C、投影面积
D、最大外围矩形面积
14、某写字楼室内天棚装饰面距设计室内地坪为3.5m,该层层高为4. 5m,满堂脚手架()。
A、不计笔
B、仅计算基本层
C、仅计算一个增加层
D、计算基本层和一个增加层
15、雨篷结构的外边线与1砖(砖规格240*115*53)外墙结构中心线的宽度为
2.2m,其建筑面积计算的原则为()。
A、不计算
B、按雨遑结构板的水平投彩面积计算
C、按雨篷的外围面积计算
D、按雨篷结构板的水平投影面积的1/2计算
二、多项选择题(5题,毎题2分,共10分。
将正确答案选项的编号填入答题卡相应位置,选对得分,不选、错选均不得分;少选无错项,每项得0.5分。
题中未作说明的工料机价格均以2010版定额本为准。
)
1、下列费用中,属于建筑工程材枓费的有()
A、周转性材料费
B、材料二次搬运费
C、材料运杂费
D、材料采购保管费
E、对材料进行一股性鉴定、检查发生的费用。
2、下列各项中属于砖基础工程量清单项目特征内容的是().
A、垫层的材料种类、厚度
B、基础深度
C、基础类型
D、砖品种、规格、强度等级
E、砂浆种类,强度等级
3、下列中不属于空腹钢构件的是()
A.钢管柱 B、H型钢柱 C、格构柱
D、蜂窝梁
E、L型钢柱
4、卷材屋面防水,定额中未考虑的因素有以下几种()。
A.附加层B、金属压条 C、接缝
D、收头
E、胶粘剂
5、楼地面工程中的零星项目适用于()。
A、楼梯侧面装饰
B、石材嵌边
C、台阶侧面装饰
D、门洞空圈
E、0.5m2以内少量分散的楼地面块料装修
三、定额套用和换算(3题,每小题5分。
共15分,题中未作说明的工料机价格均以2010版定额本为准。
)(表内计置单位统一与定额本同口径,所有计算结果均保留2位小数)
综合计算题(2题,共60分。
题中未作说明的工料机价格均以2010版定额本为准)。
计算题一(45分)
某别墅工程,设地下室一层,地上为二层框架结构。
其中,地下室部分的相关设计说明及施工图纸如下:
设计说明
(1)混凝土:除垫层以外.其余均釆用C30/P8泵送商品混凝土浇捣(含外墙、柱、基础底板及顶板);
(2)砌体:内墙采用240*115*90混凝土多孔砖,以1砖墙砌筑,砌筑砂浆为M7.5水泥砂浆;
(3)门窗:M1221洞口尺寸1200*2100。
门窗立樘与门窗幵启方向的墙面平齐,如图所示:
(4)部分室内装修做法如下表所述。
室内装修表(部分)
序
号
部位装修做法
1 地面①600*600mm地砖面层(密缝), 20mm厚1:3水泥砂浆铺贴;
②1.2mm厚JS涂科防水层,四周沿墙、柱翻高250mm;
③20mm厚1:3水泥砂浆找平层
④基房结构
2 地面
踢脚
线
①120mm高地砖面层,1:2水泥砂浆粘贴;
②基层结构
3 内墙
(含
柱面)
①耐水防霉涂料三遍:
②20mm 厚1:2水泥砂浆抹灰(遍数同定额):
③基层姑构
施工图纸(详见下页)
(一)试按照以上条件.在答卷内列式计算除楼梯间(含门洞空圈)外的地下室地面清单工程量,并根据地面做法内容;在答卷内的“分部分项工程量清单表”中,按08清单计价规范编制该地面消单。
(注:工程量计算结果均
保留2位小数)
(二)试根据以上条件,按答卷内“工程量计算及定额套用表”的要求,列式计算以下工程内容的工程,并套用相应定额(注:工程量计算结果均保留2位小数):
1、地下室底板(不包括垫层)、地下室墙和》-0.05m结构平面中LL1、LL4 梁的混凝土浇捣.以及-0.05m结构平面中LL
2、LL
3、LL5梁的模板(注:采用复合木模,模板工程量按混凝土与模板接触面的面枳计算):
2、除楼梯间(含门洞空圈)外的地下室地面防水,地面、地面踢脚线及内墙(柱)面饰面(含涂料)(注:计算涂料工程量时,不扣除构件与构件垂直相交的交接处面积.但应扣除蹒脚线所占的面积):
3、地下室的垂直运输。
计算题二(15分)
某十八层市区临街综合大楼,含地下室一层,单层建筑面积均为I500m2,其中:地下室层高5m,地上建筑首层、二层层高4.5m,其余标准层层高为3.6m, 设计室外地坪标高-1.00m.檐口底标高与屋面齐平。
该工程以清单招标方法按施工总承包形式进行发包(无专业发包)
(一)试根据上述内容,在答卷内的“工程类别及理由说明表”中填写该工程的工程类别,并说明理由。
(二)试根据上述内容和以下所提供的假设条件,结合2010版施工费用定额关于招标控制价的编制规定,以综合单价法按答卷内“工程费用计算表”所列费用项目和要求,计算该招标控制价的各项费用及工程造价(注:费用计算结果均四舍五入保留2位小数)。
假设条件:
1、该综合大楼建筑工程的清单分部分项工程费为3000万元,其中人工
费600万元、机械费250万元:施工技术措施费为500万元,其中人工费65
万元、机械费85万元:其他项目费100万元:
2、相应的材料费用已按市场信息价格考虑:相应的人工费、机械费不考
虑市场信息价格的价差因素;
3、该工程定额工期500天,拟定合同工期425天(涉及冬雨季施工因素);
4、施工场狭小.材料需考虑二次搬运因素:工程质量目标为合格工程,要
求做好竣工验收前的己完工程成品保护工作;
5、该工程民工工伤保险费和危险作业意外伤害保险费费率根据N市规定
分别为0.159%和、0.199%,取费基数为税前工程造价(但不包含此两项规费
费用自身)。
浙江省2013年度《全国建设工程造价员资格》试卷考试——建筑工程计价试题(参考答案)
一、单选题
1-5 ABDDB 6-10 BBCDB 11-15 ACDAA
二、多选题
1.CD
2.BCDE
3.ABE
4.AB
5.ACE。