n维向量,线性相关性
- 格式:ppt
- 大小:2.52 MB
- 文档页数:35


n维向量组a1a2a3a4线性相关线性相关,指的是两个或多个变量之间存在着一定程度上的相关性。
只要任意两个变量间有任何线性关系,它们就被认为是线性相关的。
维向量组a1a2a3a4之间存在线性相关性,那么关于它们的内容有:1. 维向量组a1a2a3a4可以表示为m维空间里的n个线性方程,即a1、a2、a3、a4都可以表示为:$x_1c_1 + x_2c_2 + x_3c_3 + x_4c_4 = 0$ 。
2. a1a2a3a4之间的线性关系可以表示为:一个变量值的变化会改变其他变量的值,或者说某一变量的变化会引起其他变量的变化。
3. 根据a1a2a3a4的线性相关性,在满足一定约束条件时,可以求出4个变量之间的相对关系。
4. a1a2a3a4之间的线性相关性包括两个方面:一是它们本身存在线性关系,二是它们之间存在线性关系。
5. 维向量组a1a2a3a4之间的线性相关性可以通过线性回归分析等方法来进行评估和确定。
6. 定量分析维向量组a1a2a3a4之间的线性相关性,可以通过Kendall系数法,Spearman等秩相关系数等方法来测定。
7. 维向量组a1a2a3a4之间的线性相关性可以用多元线性回归模型进行预测和分析,来验证其定量分析结果。
8. 利用维向量组a1a2a3a4之间的线性相关性可以分析多个指标之间的关系,从而实现建模和预测。
9. 如果维向量组a1a2a3a4之间的线性关系很强,那么可以用回归模型来表示,从而可以实现估算变量值,也可以给出变量的可信区间。
10. 利用维向量组a1a2a3a4之间的线性关系可以计算特征向量的投影,可以解决多维特征间相关性的研究问题,使特征维度减少,数据表达更加简洁。

向量组的线性相关性1、n 维向量由n 个数组成的有序数组()12,,,n a a a 称作一个n 维向量,记作()12,,,n a a a α= ,其中i a 称作α的第i 个坐标。
设()12,,,n a a a α= ,()12,,,n b b b β= ,当()1,2,,i i a i n b == 时,称α与β相等,记作αβ=。
称()12,,,n a a a α= 为n 维列向量,αT 为n 维行向量。
分量全为0的向量称为零向量。
向量()12,,,n a a a α= 的各分量的相反数所组成的向量,称为α的负向量,记作α-,即()12,,n a a a α=---- 。
向量加法定义:()1122,,,n n a b a b a b αβ+=+++ ;向量减法定义:()()1122,,,n n a b a b a b αβαβ-=+-=--- 。
向量α与数乘积定义;k 为任意实数,则()12,,,n k k k k αααα= n 维向量的加法和数乘运算满足下面性质(设α、β、γ表示n 维向量,k 、l 表示数量)。
(1)αββα+=+;(2)()()αβγαβγ++=++;(3)0αα+=;(4)()0αα+-=;(5)()k k k αβαβ+=+;(6)()k l k l ααα+=+。
2、向量的线性表示设12,,,s ααα ,β均为n 维向量,若存在一组数12,,,s k k k ,使得1122k k αβα=+++ s s k α,则称向量β是向量组12,,,s ααα 的一个线性组合,也称向量β可由向量组12,,,s ααα 线性表示。
3、向量组的线性相关性对于m 个n 维向量12,,,m ααα ,若存在不全为零的数12,,,m k k k ,使得11220m m k k k ααα+++= ,则称这m 个向量线性相关;否则,称它们线性无关。
通过线性相关和线性无关的定义可推出:(1)单独一个0向量,线性相关;高 数向量组的线性相关性知识点速记(2)含有0向量的向量组,线性相关;(3)单独一个非0向量,线性无关;(4)由n 个标准单位向量()11,0,0,,0=ε ,()20,1,0,,0=ε ,…,()0,,0,1n =ε 组成的向量组,线性无关。

第四章向量及向量空间§1 n维向量及其线性相关性§2 向量组的秩§3 线性方程组解的结构§4 向量空间§1 n维向量及其线性相关性●n维向量●线性相关性定义1 n 个有次序的数所组成的数组称为n 维向量,这n 个数称为该向量的n 个分量,第i 个数称为第i 个分量。
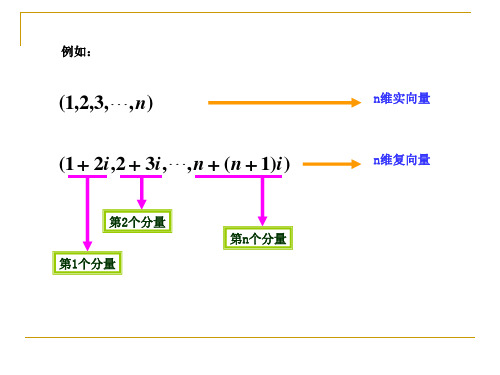
,,,12n a a a i a ◆分量全为实数的向量称为实向量◆分量为复数的向量称为复向量本书中除特别指明者外,一般只讨论实向量◆n 维向量写成一行的称为行向量◆n 维向量写成一列的称为列向量(),,,n a a a 1212 n a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭◆实数域R 上全体n 维向量组成的集合称为n 维实向量空间记为R n说明:◎行向量和列向量总被看作是两个不同的向量。
◎所讨论的向量在没有指明是行向量还是列向量时,都当作列向量。
◎通常情况下,列向量用黑色小写字母a ,b ,α,β等表示,行向量则用a ,b ,αT ,βT 表示。
◎行向量和列向量也分别称为行矩阵和列矩阵,并规定都按矩阵的运算规则进行运算。
◎若干个同维数的列向量(行向量)所组成的集合称为向量组。
11121314342122232431323334a a a a A a a a a a a a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭()1234,,,αααα=123T T T βββ⎛⎫ ⎪= ⎪⎪⎝⎭结论:含有限个向量的有序向量组与矩阵一一对应.有限向量组例如定义2 设a∈R n, k i∈R, (i=1, 2, …, m),则向量ik1a1 + k2a2 + … + k m a m称为向量组a, a2, …, a m在实数域R上的一个线性组合。
1k1, k2, …, k m 称为这个线性组合的系数.定义:若记b= k1a1 + k2a2 + … + k m a m, a2, …, a m线性表示。
则称向量b 可由向量组a1b 可由向量组a1, a2, …, a m线性表示方程组xa1 + x2a2 + … + x m a m = b有解1例:设()123100,,010001E e e e ⎛⎫ ⎪== ⎪ ⎪⎝⎭100203170001⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭123237e e e =++237b ⎛⎫ ⎪= ⎪ ⎪⎝⎭那么线性组合的系数e 1, e 2, e 3的线性组合一般地,对于任意的n 维向量b ,必有1231000010000100001n b b b b ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=+++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭123n b b b b b ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭n 阶单位矩阵E n 的列向量叫做n 维单位坐标向量.1231000010000100001n b b b b ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪=+++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭123n b b b b b ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭1000010000100001n E ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭例零向量是任何一组向量的线性组合.例向量组a 1, a 2, …, a s 中的任一向量a j (1≤j ≤s )都是此向量组a 1,a 2, …, a s 的线性组合。
