超声波检测主要定律

超声波检测(船舶教材)（幻灯片稿本编写：孟传亨）§1超声波检测物理基础1 机械振动和机械波1.1 机械振动：一个物理量的值在观测时间内不停地经过极大值和极小值的周期变化，这种变化状态称为振动。

如果振动量是个力学量，如位移、角位移等，所作的振动称之为机械振动。

图1－1(教材中的图2－1和图2－2)表示了机械振动的两个示例。

1.1.1两个表征振动的参数：周期T：完成一次全振动所需的时间，常用单位秒(s)。

频率f：单位时间内完成全振动的次数，单位为赫芝(Hz)。

1Hz＝1次/秒＝秒－1；1MHz＝106Hz。

1.1.2振动方程：最简单最基本的直线振动称为谐振动，任何复杂的振动都可视为多个谐振动的合成。

描述谐振动质点M位移y与时间t关系的谐振动方程如下：y＝Acos(ωt＋φ) （1－1）式中：y——为振动幅度在任一瞬间时t的数值；A——为振幅，是y的最大值；ω——角频率(角速度)，ω＝2πf；φ——初始相位角，即t＝0时质点M的相位；(ωt＋φ)——质点M在t时刻的相位。

可用图1－2（教材中的图2－6）来进一步说明物体谐振动时，位移是时间的正弦或余弦函数。

1.2 机械波和声波：1.2.1机械波的形成机械振动在介质中的传播称为机械波，机械振动在弹性体中的传播称之为弹性波（声波）。

图1—3（教材中的图2－3）是弹性体的模型，可用来说明机械波的形成。

1.2.2产生机械波的两个条件：1.作机械振动的波源；2.传播振动的介质。

1.2.3超声波如果以频率f来表征声波，并以人的可闻频率为分界线，则可把声波划分为次声波（f＜20Hz）、可闻声波（20Hz≤f≤20kHz）和超声波（f＞20kHz）。

在超声波检测中最常用的频率范围为0.5～10MHz。

1.2.4三个表征波动的参数：频率f：波在单位时间内通过给定点的完整波的个数称为波的波动频率；波长λ：波在一个周期内传播的距离称为波长；波速c：声波在单位时间所传播的距离称为波速。

超声波测试原理及应用超声波是频率在2104Hz 1012Hz的声波。

超声广泛存在于自然界和日常生活中，如老鼠、海豚的叫声中含有超声成分，蝙蝠利用超声导航和觅食；金属片撞击和小孔漏气也能发出超声。

人们研究超声始于1830年，F. Savart曾用一个多齿轮，第一次人工产生了频率为2.4 104Hz的超声；1912年Titanic客轮事件后，科学家提出利用超声预测冰山；1916年第一次世界大战期间P. Langevin领导的研究小组开展了水下潜艇超声侦察的研究，为声纳技术奠定了基础；1927年，R. W. Wood 和A. E. Loomis 发表超声能量作用实验报告，奠定功率超声基础；1929年俄国学者Sokolov提出利用超声波良好穿透性来检测不透明体内部缺陷，以后美国科学家Firestone使超声波无损检测成为一种实用技术。

超声波测试把超声波作为一种信息载体，它已在海洋探查与开发、无损检测与评价、医学诊断等领域发挥着不可取代的独特作用。

例如，在海洋应用中，超声波可以用来探测鱼群或冰山、潜艇导航或传送信息、地形地貌测绘和地质勘探等。

在检测中，利用超声波检验固体材料内部的缺陷、材料尺寸测量、物理参数测量等。

在医学中，可以利用超声波进行人体内部器官的组织结构扫描（B超诊断）和血流速度的测量（彩超诊断）等。

本实验简单介绍超声波的产生方法、传播规律和测试原理，通过对固体弹性常数的测量了解超声波在测试方面应用的特点；通过对试块尺寸的测量和人工反射体定位了解超声波在检验和探测方面的应用。

实验所用的仪器设备和主要器材包括：JDUT-2型超声波实验仪、GOS-620型示波器（20MHz）、CSK-IB型铝试块、钢板尺、耦合剂（水）等。

实验一、超声波的产生与传播能够产生超声波的方法很多，常用的有压电效应方法、磁致伸缩效应方法、静电效应方法和电磁效应方法等.我们把能够实现超声能量与其他形式能量相互转换的器件称为超声波换能器。

求波长的公式：λ(波长)=c(波声速)÷f(频率) 求声阻抗的公式：Z=ρ(密度)×c(波声速) 折射定律：221'1'1sin sin sin sin sin S SL L S S L L L L c c c c c ββααα==== C L1、C S1——第一介质中的纵波、横波波速 C L2、C S2——第二介质中的纵波、横波波速L α、L 'α、s 'α——纵波入射角、反射角、横波反射角 L β、s β——纵、横波折射角求斜探头入射角：sin α=C L1÷C S2×sin β 第一临界角：αⅠ=arcsin C L1÷C L2 第二临界角：αⅡ= arcsin C L1÷C s2第三临界角：αⅢ= arcsin C s1÷C L1当入射角在αⅠ～αⅡ时，钢中只有纯横波 当入射角大于αⅢ时，钢中只有表面波求波高公式：先算出二者间的差值，再加上基准值 △=20lg （H 2/H 1） 求水钢界面声强透射率：21221)(4Z Z Z Z T += 计算薄工件的衰减系数（厚度小于200mm ）：)/()(2)lg(20mm dB xm n B B n m--=δαm 、n 为底波反射次数；B m 、B n 为第m 、n 次波高 δ——反射损失；x ——薄板厚度 计算厚工件的衰减系数：)/(26)lg(2021mm dB xB B -=α计算圆盘圆辐射纵波声场的半扩散角（指向角）： θ0=arcsin1.22λ/D s ≈70λ/D s （°） 近场区长度的计算： N=D 2/4λ矩形波源辐射纵波声场的半扩散角（指向角）： ψ0=arcsin λ/a ≈57λ/a(°)近场区长度为：N=Fs/πλ=、D 2/4λ 纵波声场两种介质的近场区长度：已知水层厚度为L ，基于钢中的近场区长度： N=D s 2/4λ2-LC 1/C 2基于水中的近场区长度： N=（D s 2/4λ2-L ）C 1/C 2 未扩散区长度b=1.64N 计算平底孔回波声压：220x F F P P fs f λ=P 0：探头波源的起始声压 Fs ：探头波源面积=πD 2s/4 Ff ：平底孔缺陷的面积=πD 2f /4 X ：平底孔至波源的距离 二者回波分贝差：1221lg40x D x D f f长横孔回波声压计算公式：xD xF P P f sf 220λ=两者的分贝差：312321lg10xD x D f f球孔回波声压计算公式：xD x F P P fs f 40λ=两者的分贝差：212221lg20xD x D f f大平底面回波声压公式：xF P P sB λ20=不同距离的大平底面回波分贝差：12lg 20x x。

超声波检测级考试计算公式汇总TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-超声波检测2级基础知识计算公式超声波频率：f>20000Hz 声波频率：20Hz<f<20000Hz 次声波频率：f<20Hz金属材料超声波检测常用频率：~10MHz 机械振动：T =1f谐振动方程：y =Acos (ωt +φ)阻尼振动方程：y =A 0e −βt cos (ωt +φ0) 受迫振动方程：y =Acos (Pt +φ) 机械波主要物理量：c =λf 或λ=c /f 平面波波动方程：y =Acosω(t −xc )柱面波波动方程：y =A √x cosω(t −xc) 球面波波动方程：y =Ax cosω(t −xc ) 无限大固体介质中声速 纵波：c L =√Eρ√1−σ(1+σ)(1−2σ)横波：c s =√Gρ√12(1+σ)表面波：c R =0.87−1.12σ1+σ√E ρ12(1+σ)同一介质中:c L c s=√2(1−σ)1−2σc R c s=0.87+1.12σ1+σc L >c s >c R c L ：c s ：c R =:1:细长棒中纵波波速：c Lb =√Eρ钢中波速：c L =5900m /s c s =3230m /s 水中波速：c L =1480m /s有机玻璃波速：c L =2730m /s c s =1460m /s 液体、气体中纵波声速：c =√Bρ超声场特征值声压：P =−ωAsinω(t −x c ⁄) 声压幅值：P m =ρcωΑ=ρcu 质点振动速度：u =2πfΑ 声阻抗：Z =P u =ρc ⁄ 声强：I =P 22Z声强级（贝尔）：Δ=lg (I 2I 1⁄)分贝差（dB ）：Δ=10lg (I 2I 1⁄)=20lg (P 2P 1⁄)=20lg (H 2H 1⁄) 奈培（NP ）：Δ=ln (P 2P 1⁄)1NP= 1dB=单一平面反、透射率 声压：r =P rP 0=Z 2−Z 1Z 2+Z 1t =P tP 0=2Z 2Z 2+Z 1声强：R =(Z 2−Z 1Z 2+Z 1) T =4Z 1Z 2(Z 2+Z 1)2T+R=1 t-r=1 声压往复透射率： T =4Z 1Z 2(Z 1+Z 2)2超声波倾斜入射界面 纵波折反射定律：sinαL C L=sinα′L C L1=sinα′s C s1=sinβL C L2=sinβs C s2第一临界角：αⅠ=arcsinC L1C L2第二临界角：αⅡ=arcsin C L1C s2横波折反射定律：sinαs C s1=sinα′s C s1=sinα′L C L1=sinβL C L2=sinβs C s2第三临界角：αⅢ=arcsinC s1C L1有机玻璃/钢临界角：αⅠ=° αⅡ=° αⅢ= ° 平面波在曲界面上的反射平面波入射球面时，曲面轴线上的反射声压：P x =P 0|f x ±f| ,f=r/2平面波入射到柱面时，曲面轴线上的反射声压：P x =P 0√|f x ±f| ,f=r/2平面波在曲界面上的反射平面波入射球面透镜时，曲面轴线上的反射声压： P x =tP 0|f x ±f| ,f=r/2平面波入射到柱面透镜时，曲面轴线上的反射声压： P x =tP 0√|f x ±f| ,f=r/2超声波衰减薄板（t<200mm ）工件衰减系数：α=20lg (B m B n ⁄)−δ2(n −m )x厚>200mm 板材及轴类件衰减系数：α=20lg (B 1B 2⁄)−6−δ2x纵波发射声场圆盘波源近场区长度：N ≈D s 24λ=F s πλ波速指向性和半扩散角半扩散角：θ0=arcsin 1.22λD s ⁄≈70λD s ⁄ 波束未扩散区：b ≈D s 22.44λ=1.64N矩形波源的纵波声场YOZ半扩散角：φ0=arcsinλ2b ≈57λ2bXOZ半扩散角：θ0=arcsinλ2a ≈57λ2a矩形波源的近场区长度：N=F sπλ纵波近场区在两种介质中分布水/钢近场区：基于钢计算N′=N钢−L C水C钢=D s24λ钢−L C水C钢基于水计算N′=（N水−L)C水C钢=(D s24λ水−L)C水C钢规则反射体平底孔直径一定，距离增加一倍，其回波下降12dB平底孔距离一定，直径增加一倍，其回波升高12dB长横孔直径一定，距离增加一倍，其回波下降9dB长横孔距离一定，直径增加一倍，其回波升高3dB短横孔直径和长度一定，距离增加一倍，其回波下降12dB 短横孔直径和距离一定，长度增加一倍，其回波上升6dB 短横孔长度和距离一定，直径增加一倍，其回波升高3dB 球孔直径一定，距离增加一倍，其回波下降12dB球孔距离不变，直径增加一倍，其回波上升6dB大平底面距离增加一倍，其汇报下降6dB。

精心整理一、1、示波屏上的波高与声压成正比。

既：△=20lgP2/P1=20lgH2/H1(1NP=8.68dB1dB=0.115NP)2、声压反射率r和投射率t分别为：34567二1、近场区长度：N=D2S /4λ=R2S/λ=FS/πλ=FS?/Cλ2、圆盘源辐射的纵波声场的第一零值发散角；θ0=arcsin1.22λ/Ds≈70λ/Ds3、波束未扩散区与扩散区：b=1.64N4、矩形波源的近场区长度N=Fs/πλ，未扩散区b=1.64N，半扩散角θ0=arcsinλ/2a≈57λ/2a，5、近场区在两种介质中的分布；公式N=D2S/4λ只适用均匀介质。

在水、钢两种介质中，当水层厚度较小时，进场区就会分布在水、钢两种介质中，设水层厚度为L，则钢中剩余进场区长度N为：N=N2-LC1/C2=D2S/4λ-LC1/C2，612（一3（分别为B=70、C=30、D=15mm）。

4、信噪比；△=20lgH信/H噪。

四1、（1）按声程调节扫描速度时：一次波探伤时（τ∫≤T），缺陷至入射点的声程x∫=nτ∫，则缺陷在工件中的水平距离为：l=x∫sinβ=nτ∫sinβ、深度为：d∫=x∫cosβ=nτ∫cosβ。

二次波探伤T＜τ∫∫≤2T时，则缺陷在工件中的水平距离为：l=x∫sinβ=nτ∫sinβ、∫深度为：d=2T-x∫cosβ=2T-nτ∫cosβ。

∫（2）按水平调节扫描速度时：一次波探伤（τ≤T）时，∫2h=[(Kd)2+(r+d)2]0.5-rl=rπθ/180=rπ/180*tg-1Kd/r+d结论：当探头从圆柱曲面内壁作周向探测时，弧长l总比水平距离l值小，但深度h却总比平板工件中的缺陷深度d值大。

（注意，如缺陷深度h大于壁厚，则为焊缝杂波）3、最大探测壁厚；Tm/D≤1/2(1-sinβ)≤1/2(1-K/(1+K2)0.5一般把筒体可探测的内外半径范围定位r/R≥80%4、不同距离处的大平底与平底孔回波分贝差为；△B?=20lgP B/P?=20lg2λχ2?/лD2?χB+2α(χ?-χB)α—材质衰减系数；χ?—探测面至缺陷的距离；χВ—探测面至底面的距离（工件的厚度）不同平底孔、距离的回波分贝差为；5（1（26、S2将位于管子的缺陷波F内（一次波）F外（二次波）之后，这样，有利于对缺陷判别。

一、1、示波屏上的波高与声压成正比。

既：△=20lgP2/P1=20lgH2/H1(1NP=8.68dB1dB=0.115NP)2、声压反射率r和投射率t分别为：r=Pr /PO=Z2-Z1/Z2+Z1t=Pt/PO=2Z2/Z2+Z13、声强反射率R和投射率T分别为：R=r2=(Z2-Z1/Z2+Z1)2T=4Z1Z/(Z2+Z1)2由以上几式得：t-r=1T+R=14、声压往复透射率T往：探头接收到的回波声压Pa与入射波声压PO之比。

既：T往=Pa/PO=4Z1Z/(Z2+Z1)25、反射、折射定律：sinαL /CL1=sinα1L/CL1=sinα1S/CS1=sinβL/CL2=sinβS/CS26、第一临界角。

αⅠ=arcsinCL1/CL2第二临界角。

αⅡ=arcsinCL1/CS2第三临界角：αⅢ=arcsinCS1/CL17、（1）薄板工件的衰减系数测定：α=(20lgBm/Bn-δ)/2x(n-m)对于多次反射：α=[20lgBm/Bn-δ(n-m)]/2x(n-m)（2）厚板工件的衰减系数测定：α=(20lgB1/B2-6-δ)/2x对于2次波、3次波；α=(20lgB2/B3-3.5-δ)/2x。

对于1次波、3次波；α=(20lgB1/B3-9.5-δ)/4x。

二1、近场区长度：N=D2S /4λ=R2S/λ=FS/πλ=FS?/Cλ2、圆盘源辐射的纵波声场的第一零值发散角；θ=arcsin1.22λ/Ds≈70λ/Ds3、波束未扩散区与扩散区：b=1.64N4、矩形波源的近场区长度N=Fs/πλ，未扩散区b=1.64N，半扩散角θ=arcsinλ/2a≈57λ/2a，5、近场区在两种介质中的分布；公式N=D2S/4λ只适用均匀介质。

在水、钢两种介质中，当水层厚度较小时，进场区就会分布在水、钢两种介质中，设水层厚度为L，则钢中剩余进场区长度N为：N=N2-LC1/C2=D2S/4λ-LC1/C2，6、横波近场区长度；方形N=FS /πλs2*cosβ/cosα圆形N=D2/4λs2*cosβ/cosα横波声场中，第二介质中的近场区长度：N`=N-L2=FS/πλs2*cosβ/cosα-L1tgα/tgβF S-波源面积λs2-介质Ⅱ中横波波L1-入射点至波源的距离L2-入射点至假想波源的距离半扩散角；对于圆片形声源：?0=arcsin1.22λS2/DS=70λS2/DS对于矩形正方形声源：?0=arcsinλS2/2a=57λS2/2a三1、计算垂直线性误差D=（∣d1∣+∣d2∣）%。

超声波探伤常用计算公式标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]一、1、示波屏上的波高与声压成正比。

既：△=20lgP2/P1=20lgH2/H1(1NP= 1dB=2、声压反射率r和投射率t分别为：r=Pr / PO=Z2-Z1/Z2+Z1t=Pt/ PO=2Z2/Z2+Z13、声强反射率R和投射率T分别为：R=r2 =(Z2-Z1/Z2+Z1)2 T=4Z1Z/(Z2+Z1)2由以上几式得：t-r=1 T+R=14、声压往复透射率T往：探头接收到的回波声压Pa与入射波声压PO之比。

既：T往=Pa /PO=4Z1Z/(Z2+Z1)25、反射、折射定律：sinαL /CL1=sinα1L/CL1= sinα1S/CS1=sinβL/CL2=sinβS/CS26、第一临界角。

αⅠ=arcsinCL1/CL2第二临界角。

αⅡ=arcsinCL1/CS2第三临界角：αⅢ=arcsinCS1/CL17、（1）薄板工件的衰减系数测定：α=(20lgBm/Bn-δ)/2x(n-m)对于多次反射：α=[20lgBm/Bn-δ(n-m)]/2x(n-m)（2）厚板工件的衰减系数测定：α=(20lgB1/B2-6-δ)/2x 对于2次波、3次波；α=(20lgB2/δ)/2x。

对于1次波、3次波；α=(20lgB1/δ)/4x。

二1、近场区长度：N=D 2S /4λ= R 2S /λ= F S /πλ= F S /C λ 2、圆盘源辐射的纵波声场的第一零值发散角； θ0=λ/Ds ≈70λ/Ds 3、波束未扩散区与扩散区：b=4、矩形波源的近场区长度N=Fs/πλ，未扩散区b=， 半扩散角θ0=arcsin λ/2a ≈57λ/2a ，5、近场区在两种介质中的分布；公式N=D 2S /4λ只适用均匀介质。

在水、钢两种介质中，当水层厚度较小时，进场区就会分布在水、钢两种介质中，设水层厚度为L ，则钢中剩余进场区长度N 为：N=N 2-LC 1/C 2= D 2S /4λ- LC 1/C 2，6、横波近场区长度；方形 N=F S /πλs2*cos β/cos α圆形 N=D 2/4λs2*cos β/cos α横波声场中，第二介质中的近场区长度： N`=N-L 2= F S /πλs2*cos β/cos α-L 1tg α/tg βF S -波源面积 λs2-介质Ⅱ中横波波 L 1-入射点至波源的距离 L 2-入射点至假想波源的距离半扩散角；对于圆片形声源：0=λS2/D S =70λS2/D S对于矩形正方形声源：0=arcsin λS2/2a=57λS2/2a三1、计算垂直线性误差D=（∣d 1∣+∣d 2∣）% 。

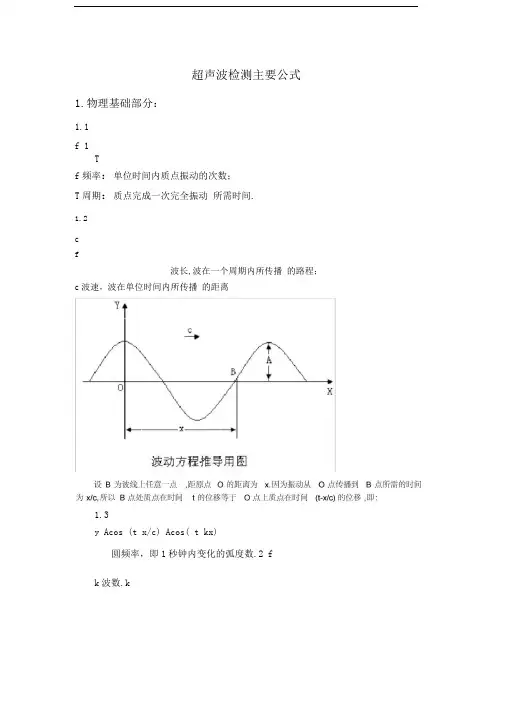
超声波检测主要公式1.物理基础部分：1.1f -Tf频率：单位时间内质点振动的次数；T周期：质点完成一次完全振动所需时间.1.2c波长,波在一个周期内所传播的路程; c波速，波在单位时间内所传播的距离Array波动方程推导用图设B为波线上任意一点，距原点0的距离为X.因为振动从0点传播到B点所需的时间为x/c,所以B点处质点在时间t的位移等于0点上质点在时间(t-x/c)的位移,即：1.3y Acos (t x/c) Acos( t kx)圆频率,即1秒钟内变化的弧度数k波数.^ -—c1.42I _E m2ZI 声强.在垂直声波传播方向上，单位面积上在单位时间内通过的平均声能. p 声压弹性质点在传播声时，相邻质点所受到的附加 压力. Z 声阻抗.其能直接表示介质的声 学性质.数值上Zc1.5dB 20 lg -P l 20lg 也p 2 H 2P 1和p 2两个比较声压.分母中的p 2为基准声压.已和H 2两个比较的反射回波幅 度.分母中的H 2为基准反射回波幅度. 1.6 声速c EkVE 介质的杨氏弹性模量，等于介质承受的拉应力F / S 与相对伸长 L/L 之比. 即:E 3L/ L介质的密度.等于介质的质量M 与其体积V 之比,即 M/Vk 与介质的泊松比有关的常数.介质的泊松比，等于介质横向相对缩短 1 d/d 与纵向相对伸长 L/L之比，即 1/1.7 在钢中c/c t1.82; C r 0.92c t1.8反射折射定律sin I sin isin tsin isin tc nc i1c t1c i2c t2l , h t 分别是第一介质的纵波入射角，纵波反射角，横波反射角C l1,C t1,Q 2,Q 2分别是第一介质纵波速 度,横波速度，第二介质纵波速度,横波速度i , t分别是第二介质纵波折 射角,横波折射角1.9第一临界角:纵波斜入射时，第二介质折射纵波的折 射角等于90°时的纵波入射角为第一临界角。

说明超声波反射,折射定律和和式中各参数的物理意义超声波在工业、医疗、科研等多个领域具有广泛的应用。

了解超声波的反射、折射定律及其相关参数的物理意义，有助于我们更好地应用这一技术。

本文将详细解释超声波反射、折射定律以及和式中各参数的物理意义。

一、超声波反射定律超声波在遇到界面时，会发生反射现象。

超声波反射遵循以下定律：1.入射角等于反射角：当超声波从一个介质入射到另一个介质时，入射角（入射波与法线的夹角）等于反射角（反射波与法线的夹角）。

2.反射波与入射波在同一平面内：反射波、入射波和法线三者共面。

3.反射系数：反射系数是描述反射波与入射波幅度比的一个参数，用R表示。

其计算公式为：R = (反射波幅度) / (入射波幅度)反射系数的取值范围在-1到1之间，正值表示同相位反射，负值表示反相位反射。

二、超声波折射定律当超声波从一个介质进入另一个介质时，会发生折射现象。

超声波折射遵循以下定律：1.斯涅尔定律：入射角（θ1）和折射角（θ2）的正弦值之比等于两个介质的波速之比，即：sin(θ1) / sin(θ2) = v1 / v2其中，v1和v2分别为两个介质的波速。

2.折射波与入射波在同一平面内：折射波、入射波和法线三者共面。

3.折射系数：折射系数是描述折射波与入射波幅度比的一个参数，用n表示。

其计算公式为：n = (折射波幅度) / (入射波幅度)折射系数的取值范围在0到1之间。

三、和式中各参数的物理意义在超声波反射、折射定律中，和式通常表示为：E = E0 * (R * cos(θ1) + n * cos(θ2))其中，E表示接收到的超声波总能量，E0表示入射的超声波能量，R表示反射系数，n表示折射系数，θ1表示入射角，θ2表示折射角。

各参数的物理意义如下：1.E0：入射的超声波能量，反映超声波在传播过程中的强度。

2.R：反射系数，描述反射波与入射波的关系，用于分析反射波的强度和相位。

3.n：折射系数，描述折射波与入射波的关系，用于分析折射波的强度。

超声波检测主要公式1.物理基础部分 :1.11fTf频率：单位时间内质点振动的次数;T周期：质点完成一次完全振动所需时间 .1.2cf波长 ,波在一个周期内所传播的路程;c波速 ,波在单位时间内所传播的距离设 B 为波线上任意一点 ,距原点 O 的距离为 x.因为振动从 O 点传播到 B 点所需的时间为 x/c,所以 B 点处质点在时间 t 的位移等于 O 点上质点在时间 (t-x/c)的位移 ,即:1.3y A cos (t x / c) A cos( t kx)2圆频率 ,即1秒钟内变化的弧度数 . 2 fT2k 波数 .kc1.4Ip m 2 2ZI 声强 .在垂直声波传播方向上 ,单位面积上在单位时间 内通过的平均声能 . p 声压.弹性质点在传播声时 , 相邻质点所受到的附加 压力. Z 声阻抗 .其能直接表示介质的声 学性质 .数值上 Zc1.5dB 20 lgp 120lg H1p 2 H 2p 1和 p 2 两个比较声压 .分母中的 p 2为基准声压 . H 1和H 2 两个比较的反射回波幅 度.分母中的 H 2为基准反射回波幅度 .1.6声速 cE kE 介质的杨氏弹性模量 , 等于介质承受的拉应力F / S 与相对伸长L/ L 之比.即 : EF / SL / L介质的密度 .等于介质的质量 M 与其体积 V 之比 ,即M / Vk 与介质的泊松比有关的常数 .介质的泊松比 , 等于介质横向相对缩短1d / d 与纵向相对伸长L / L之比 ,即 1 /1.7在钢中 c l / c t 1.82;c r 0.92c t1.8反射折射定律sinsin, sin tsin lsinlltcl1cl 1ct1cl 2ct 2l ,l ,, t 分别是第一介质的纵波 入射角 ,纵波反射角 ,横波反射角 .c l1 ,c t1, c l 2 , c t 2 分别是第一介质纵波速度 ,横波速度 , 第二介质纵波速度 ,横波速度l ,t分别是第二介质纵波折 射角 , 横波折射角1.9第一临界角 : 纵波斜入射时，第二介质折射纵波的折射角等于 90o时的纵波入射角为第一临界角。

常用计算公式1、 周期（T ）： fT 1=单位为秒（ｓ） 2、波长（λ）、频率（ｆ）、波长（λ）之间的关系式：fC=λ C=λ·f λ=C/f f=C/λ波速大，波长大,C ↑ λ↑；频率小，波长越长，f ↓ λ↓。

3、近场区长度：直探头的近场区长度：πλλλλAD D N =≈-=44222 式中 D ——为圆形压电晶片的直径；λ——为超声波波长；A ——方晶片（或矩形晶片）面积。

斜探头的近场区长度：αβπλπλCos Cos A A N •==式中 A 0——晶片折射后的有效面积；λ——为超声波波长；A ——晶片面积；β、α——折射角、入射角。

非扩散的区域为近场长度（N ）的1.67倍，大于1.67 N 为扩散区。

4、声束指向角：圆盘声源声束指向角DDλλθ7022.1sin 10≈=-式中 D ——为晶片的直径；λ——为超声波波长。

方晶片声束指向角计算式：aaλλθ5708.1sin 10≈=-5、分贝差：2121lg 20lg20H H P P ==∆ （dB ） 6、声压反射率（r ）：21120Z Z Z Z P P r r +-==；声压透射率（t ）：12202Z Z Z P P t t+==；声压往复透射率（ＴP）：2212100)(4Z Z Z Z P P P P P P T t a t a P +=⋅==7、反射定律：入射角的正弦与反射角的正弦之比等于声速之比1'1'1T TL L L C Sin C Sin C Sin ααα==折射定律：入射角的正弦与折射角的正弦之比等于声速之比8、材质的衰减系数：Bm n mndB V ⨯-)(2g 201)n m (－－＝　α （单位：dB/mm ）9声压反射率及当量：（1）大平底：F22 g 201X dB λπΦ∆　＝、(2)平底孔：f A A f A BX X P P d ΦΦ==∆Φlg 40lg 20fAA f X X g 401lg 40+ΦΦ=当量：4010dBAf A fX X ∆••Φ=Φ(3)长横孔：33lg 10lg 20f A A f A X X P P dB ΦΦ==∆ΦfA A f X X g 301lg 10+ΦΦ=当量：10310)(dBAf A f X X ∆••Φ=Φ（4）短橫孔：4242lg10lg20fA A Af f AXL X L P P dB 短短短ΦΦ==∆Φ当量：10424210dB Af fA A f XL X L ∆•Φ=Φ短短（5）球孔：22lg20lg 20fA Af A d X d X d P P dB ==∆221T T L L L C Sin C Sin C Sin ββα==当量：20210)(dB Af A f X X d d ∆••=（短橫孔、球孔在钢轨探伤中较少运用） 例题：1. 一个垂直性好的探伤仪，荧光屏上波幅为80％，衰减24dB 后波幅为多少？ 解：由公式21g201P P dB ＝得 280g20124P ＝ P 2＝5 答：衰减24dB 后波幅有5％。