当前位置：文档之家 › 机械设计基础 南理工

机械设计基础 南理工

  • 格式：ppt
  • 大小：5.85 MB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

南京理工大学机械设计基础(上)答案_(8)[1]

南京理工大学机械设计基础(上)答案_(8)[1]

rb1 = r1 cos α =
mz1 cos 20 o 2
z3 i z1 14 = i14 = i15 ⋅ i54 = 15 = z z i45 25 1 + 2′ 3 z4 z2 ω 150 × 25 ω4 = 1 = = 267.85rad / s i14 14 1+
方向与 ω 1 相同。 九． 解： 1．
cos β =
mn ( z1 + z 2 ) 2(20 + 48) = = 0.9927 2a 2 × 68.5 β= 6.93. z v1 = z1 20 = = 20 3 cos β 0.9927 3
五、2、静平衡至少需要一个平衡质量 动平衡至少需要两个平衡质量 3、减小速度波动，增加惯性以通过死点，飞轮最好安装在高速轴上。 六、解：
n4 − n H 45 × 50 45 = = n 2 ' − n H 30 × 50 30
令 n4 转向为正 则 20
− nH 45 6 = − 20 − n H 30 1000 r = −66.67 15 min
nH = −
四、解： 1． m
转向与 n4 相反。
a=
2
( z1 + z 2 ) =
南京理工大学课程考试答案及评分标准
2、
课程名称：
机械设计基础（I）
学分：3.0 大纲编号： 012241041 满分分值： 100 考试时间： 120 分钟
a=
m n ( z1 + z 2 ) 2 cos β
试卷编号：01224104108 考试方式： 闭卷
一、 1、AB、CD 之一为虚约束；K、K‘之一为虚约束；G 处为局部自由度； H、H‘之一为虚约束。 F=3n-2pL-pH=3×5-2×6-2=1 2、A、B 之一为虚约束 CDEFG、IJKLH 之一为虚约束 F=3n-2pL-pH=3×5-2×7-0=1 二、 （1）lAB>lCD 时为转动导杆机构 （2）lAB<lCD 时为摆动导杆机构 三、 （1）η为理论轮廓 （2）基圆 r0

南京理工大学机械设计基础(上)答案 (10)

南京理工大学机械设计基础(上)答案 (10)


1 2
10

50
10

260(mm)


1 2
Z1tga1
tg
Z2 tga2
tg 1.4639
第1页 共2页
南京理工大学课程考试答案及评分标准
课程名称： 机械设计基础（Ⅰ）
学分：3.0 教学大纲编号： 012241041
试卷编号： 012124104110 考试方式： 闭卷 满分分值： 100 考试时间： 120 分钟
10 cos
15.7(mm) 10
cos
20

29.5(mm)来自a12 mZ1

Z2
1 2
10

(20

50)

350(mm)
（3）
a a 2 cos20.8a8a
c3o5s1(mm3)50 352

c
os20

0.9343534
南京理工大学课程考试答案及评分标准
课程名称： 机械设计基础（Ⅰ）
学分： 3.0 教学大纲编号： 012241041
试卷编号： 01224104110 考试方式： 闭卷 满分分值： 100 考试时间： 120 分钟
一、（每题 5 分，共 10 分） 1． F=3x5-2x7-0=1 2． F=3x5-2x7-0=1
以构件 2 (滑轮) 为示力体,进行力分析: R12 方向垂直向上,切于摩擦圆右侧
R12 Q P
R12

0

Q
D 2

P

D 2
P 50 0 Q 50 o
提升重物时的效率：

南京理工大学机械设计基础(下)答案01224104209

南京理工大学机械设计基础(下)答案01224104209
6
试卷编号： 01224104209
一.填空题(每题 2 分) 1.计算载荷等于名义载荷乘以载荷系数. 2. d1 (小径), d 2 (中径) 3.压溃、剪切(断) 4.成形联接、弹性环联接 5.定位、轻载联接和安全销 6.链节距偶数倍长 7. d1 =
P 180o 2 sin z1
8.点蚀和齿跟折断 9.磨损和胶合 10． P, Pν和ν 二.简答题 1.⑴ σ m =
Fr 3
σ max 应力不对称程度 σ min σ max :最大应力, σ min :最小应力
2.干摩擦、边界摩擦、流体摩擦和混合摩擦.2 分
②定位不准确 ⑤密封槽不对
(2 分) (2 分)
3分 ③轴承无法拆卸 (1 分) ⑥静止件与运动件相碰 (2 分)
3分 3.带靠两边拉力差工作,带分别在紧边和松边时弹性伸长量不同,因此带在包角范围内必然有收缩或伸 长,与带轮表面产生相对滑动,这种现象称为弹性滑动现象.(3 分) 弹性滑动现象降低了带传动效率,加速带磨损,并使两带轮的圆周速度不相等.(2 分) 4.转轴:承受弯矩和扭矩,例如齿轮轴.(2 分) 传动轴:传递扭矩,汽车上的传动轴.(1 分) 心轴:只承受弯矩,自行车前轴(2 分) 5.验算 P 值:保证摩擦副表面有一层润滑油膜(1 分)
2.略 3.⑴1 为左旋,2 右旋 ⑵逆时针,右旋 ⑶ (2 分) (2 分)
2
2
2
2
σ max + σ min
2 σ max − σ min ⑵σ m = 应力变动部分 2
⑶γ =
应力不变部分
1分 1分 2分 1分 4.①轴肩过高 ④没有定位
Ft 2
Fr 2 Fa 2
3分 (2 分) (1 分)

南京理工大学机械设计基础(宋梅丽)——滚动轴承

南京理工大学机械设计基础(宋梅丽)——滚动轴承
内、外圈、滚动体: GCr15 、 GCr15-SiMn 等 轴 承 钢 ， 热 处 理 后 硬度：HRC60~65 保持架:低碳钢板冲压而成，高速轴承多采用有色金 属（如黄铜）或塑料、聚四氟乙烯保持架。
21
三、滚动轴承的特点
优点： 1）f小起动力矩小，η高
2）运转精度高（可用预紧方法消除游隙）
3）轴向尺寸小
内径代号 直径系列代号
宽度系列代号 类型代号
29
（1）轴承类型
基本代号右起五位
1 —调心球轴承 3 —圆锥滚子轴承 5 —推力球轴承 6 —深沟球轴承 7 —角接触球轴承
N —圆柱滚子轴承
30
（2）尺寸系列
基本代号右起三、四位
1）直径系列——右起第三位 表示轴承有相同内径时，可有不同的外径
31
2）宽度系列——右起第四位 表示同一内径和外径的轴承可以有不同的宽度
——圆锥滚子轴承3类（n较低时） Fr较大，Fa较小时 ——深沟球轴承
Fa较大，Fr较小时 ——深沟球轴承+推力球轴承 推力角接触轴承
3）要求n<nlim——极限转速 6、7、N——nlim较高 5——nlim较低
4）轴的刚性较差，轴承孔不同心——调心轴承
5）便于装拆和间隙调整——内、外圈分离的轴承 6）3、7两类轴承应成对使用，对称安装 7）旋转精度较高时——较高的公差等级和较小的游隙 8）优先考虑用普通公差等级的深沟球轴承
（5）推力球轴承——5 只能承受轴向载荷。为防止钢球 与滚道间滑动，工作时必须加一 定的轴向载荷。
二、滚动轴承的代号
基本代号是轴承代号的基础。前置代号和后置代号都是轴承代 号的补充，只有在遇到对轴承结构、形状、材料、公差等级、 技术要求等有特殊要求时才使用，一般情况可部分或全部省略。

机械设计基础学位考试大纲含模拟试卷

机械设计基础学位考试大纲含模拟试卷
南京理工大学成人本科教学 《机械设计基础》考试大纲
一、课程的教学目标与基本要求
本课程通过理论教学使学生掌握最常用机构的组成形式、机构的运动特性、 选用原则、 机器动力学方面的基本理论和基本知识，并具有初步的分析和设计能 力。掌握通用机械零件的设计原理、方法和机械设计的一般规律，具有设计一般 通用零部件和一般机器装置的能力；逐渐形成规范的设计思想和逻辑思维能力； 具有运用标准、规范、手册和查阅有关技术资料的能力；掌握典型机械零件的实 验方法及技能； 了解一些机械领域的新成果和发展动向。培养学生掌握机械设计 的基本理论、基本方法、基础知识和具备一定的机械设计基本技能。
难点 1）周转轮系和复合轮系的传动比的计算 第 12 章轴 重点 1）轴的类型与特点，心轴、转轴、传动轴的定义概念 2）轴上零件常用轴向和周向定位方法，轴的结构设计原则 3）按扭矩进行轴的强度计算方法 4）轴的弯扭矩强度计算方法，当量弯矩和当量弯矩折算系数 5）轴的刚度计算原则 难点 1）轴的结构改错 2）轴的弯扭矩强度计算方法 第 13 章 轴承 重点 1）滑动轴承中摩擦的分类 2）向心滑动轴承的类型、结构与特点 3）常用滑动轴承轴瓦和轴承衬的材料与特点 4）滑动轴承轴瓦上油沟开设的原则，润滑剂选择原则和润滑装置 5）非全液体摩擦滑动轴承的计算的内容及意义 6）滚动轴承的结构与特点 7）常用滚动轴承的类型、特点及选用原则 8）常用轴承代号及含义 9）滚动轴承的载荷特点及失效形式 10）滚动轴承的额定寿命、当量动载荷、额定动载荷 11）角接触滚动轴承的派生轴向力和实际轴向载荷 12）滚动轴承的寿命计算 13）滚动轴承组合结构设计的原则，轴系组合结构改错 难点 1）非全液体摩擦滑动轴承的计算 2）角接触滚动轴承派生轴向力和实际轴向载荷计算 3）滚动轴承支承轴系的组合结构设计 第 14 章联轴器、离合器与制动器 重点 1） 联轴器、离合器与制动器作用及特点 2） 联轴器的常用类型、特点及选用 3） 离合器的类型及特点 4） 制动器的类型和工作原理 难点 1）联轴器、离合器与制动器的合理选用

机械设计基础 南理工7

机械设计基础 南理工7

P P P

d 1 1 d 1 d d 2 2 d 2 d d d d
hh h
LL L
L=nP(n=2) L=nP(n=2) L=nP(n=2)
dd d dd 2 2 d2 dd 1 1 d1


7）螺旋升角ψ(lead angle)—— 中径圆柱面上螺旋线的切线与垂直 于螺旋线轴线的平面的夹角：
内 内 内 螺 螺 螺 纹 纹 纹
矩形螺纹 (square thread)
内 内 内 螺 螺 螺 纹 纹 纹
3° 3° 3°
d d d d d2 d 22 d d1 d 11
P P P
P P P
d d d d d2 d 22 d d1 d 11
外 外 外 30° 螺 30° 螺 30° 螺 纹 P 纹 P 纹 P
2008年4月12日
3）螺钉(cap screw joints) 与螺栓区别——要求螺纹部分直径较粗;要求全螺纹
RR tt XX bb
dd k k nn
ll
dd
2008年4月12日
4）紧定螺钉(withstand screw) 锥 端——适于零件表面硬度较低不常拆卸场合 平 端——接触面积大、不伤零件表面，用于顶紧硬度较大 的平面，适于经常拆卸 圆柱端——压入轴上凹抗中，适于紧定空心轴上零件的位置 轻材料和金属薄板


4）螺距P (pitch) —— 螺纹相邻两牙型上对应点间的轴向距离。
5）导程L(lead) —— 螺纹上任一点沿同一螺旋线旋转一周移 动的轴向距离。
6）线数n (number of threads) —— 螺纹螺旋线数目，一般为便于
制造n≤4。 L=nP 。

南京理工大学机械设计基础(下)试卷01224104206

南京理工大学机械设计基础(下)试卷01224104206

3.
图示传动中，蜗杆 1 （左旋）主动，转向如图所示。为使轴Ⅱ、Ⅲ上传动件轴向力抵消一 部分，试确定： （1）蜗轮 2 的旋向和转向。 （2）斜齿轮 3 、 4 的旋向和转向。 （3）用图表示轴Ⅱ上传动件的各分力。 （4）圆锥齿轮 5 应如何配置。 （即圆锥齿轮 5 应在哪个位置）（12 分） 。
1
4.
（1）分析图示结构设计的错误（用数字标出并说明） 。 （2） 画出正确结构（10 分）
2的热平衡核算不满足要求时，可以采用哪些措施？ 3、 齿轮传动产生动载荷的原因是什么？ 4、 三角带传动中，为什么要验算下列几项： （1） 5m / s ≤ ν ≤ 25m / s （2） δ 1 ≥ 120
o
考试时间： 120 分钟
组卷年月： 2002.04 组卷教师：陈敏 审定教师：范元勋 一．选择题： 1.5 分/题，共 12 分） （ 1．柱销式联轴器是属于▁▁▁联轴器。 （1）固定式 （2）可移式 （3）弹性 （4）安全 2．三角带传动中带轮最常用的材料是▁▁▁。 （1） A3 （2） 45 号钢 （3） HT 15 − 33
（3） D1 ≥ Dmin 5、 说明螺栓联接，螺钉联接的结构特点及其应用上的不同之处。 6、 设计非液体摩擦向心滑动轴承应验算什么？ 四、分析计算和结构改错题： 1．轴支承在 30314 滚动轴承上，轴端锥齿轮所受的轴向力为 Fa ， （自己确定其方向） 。左轴承 （4）塑料 记为 1 ，右轴承记为 2 ，如图示安装。 （1）说明轴承代号的含义。 （2）若轴承径向力 R1 > R2 ，试写出两轴承上轴向载荷的计算式。 （12 分）
'
2.
其传递的扭矩 T = 1200 N .m ， 若使用 M 16 图示刚性联轴器， 螺栓孔分布圆直径 D = 160mm ， 的普通螺栓（螺纹内径 d1 = 13.84mm ） ，被联接件接合面的摩擦系数 f = 0.25 ，防滑系数

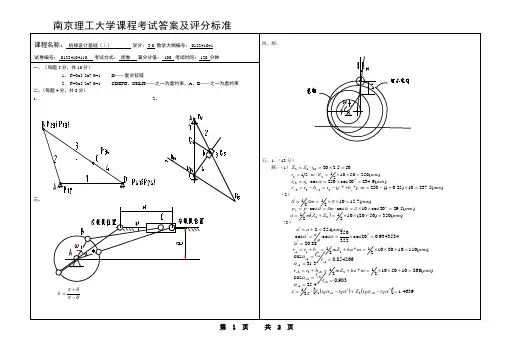
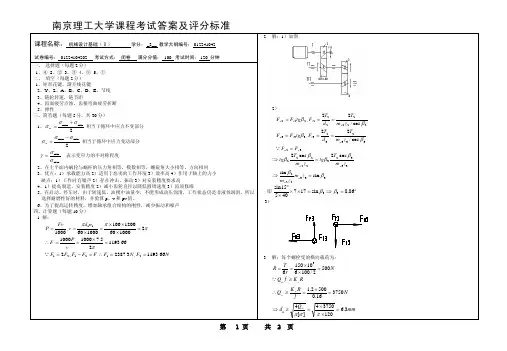
南京理工大学机械设计基础(下)答案01224104202

南京理工大学机械设计基础(下)答案01224104202
2）危险轴承的寿命：
Lh =
16670 f t c ε 16670 1 × 39800 10 / 3 ( ) = ( ) ≈ 206010.9h n fp p 1000 1 × 2349.97
5. 解：1 处：定位高度超过轴承内圈厚度 2 处：轴长应比轮毂处稍短 3 处：同 1 处 4 处：没有起到固定作用 5 处：应为梯形槽 6 处：转动件与静止件接触
南京理工大学课程考试答案及评分标准
2. 解：1）如图
课程名称：
机械设计基础（Ⅱ） 考试方式： 闭卷
学分： _3__ 教学大纲编号： 012241042 满分分值： 100 考试时间： 120 分钟
试卷编号： 01224104202
一、 选择题（每题 2 分） 1、④ 2、② 3、③ 4、③ 5、① 二、 填空（每题 2 分） 1、矩形花键，渐开线花键 2、Y、Z、A、B、C、D、E，节线 3、链轮转速，链节距 4、齿面疲劳点蚀，齿根弯曲疲劳折断 5、弹性 三、简答题（每题 5 分，共 30 分） 1、 σ m =
第 2
页
共
2
页
pp一选择题每题2分12345二填空每题2分1矩形花键渐开线花键2yzabcde节线3链轮转速链节距4齿面疲劳点蚀齿根弯曲疲劳折断5弹性三简答题每题5分共30分sssm12minmax相当于循环中应力不变部分s2minmaxss?a相当于循环中应力变动部分maxminss表示变应力的不对称程度2在主平面内蜗轮与蜗杆的压力角相等模数相等螺旋角大小相等方向相同3优点
2）
σ max + σ min
2
Fa 2 = Ft 2 tgβ 2 , Ft 2 = Fa 3 = Ft 3 tgβ 3 , Ft 3 =
相当于循环中应力不变部分

南京理工大学机械设计基础(上)答案 (6)

南京理工大学机械设计基础(上)答案 (6)

试卷编号:0122410406 考试方式: 闭卷
ω 6 = ω 6′
i6′7 =
一. 1.B 2.A 3.C 4.A 5.C 6.C 7.C 8.B 9.B 10.A 二. 1.周期性速度波动;非周期性速度波动 2.原动件;等于 3.压力角;越好 4.法;基 5.定轴轮系;周转轮系 三. 1. ON 1 和 ON 2 分别为轮 1 和轮 2 的两齿廓在节点处的曲率半径 所以,
四. 1.分布于该回转件上各个质量的离心力的合力等于零;同时,离心力所引起的力偶的合力偶矩也等于 零. 2.1)主动轴与中间轴的夹角必须等于从动轴与中间轴的夹角,即 β 1 = β 3 中间轴两端的叉面必须位于同一平面内. 五. 1.将 2 处高副转化为低副 2.
F=3×11-2×16-0=1
其中:E 为复合铰链;B 为局部自由度;I,J 及其相连构件为虚约束 2. (1)1,2,2,3 为周转轮系,轮 4 的轴线为行星架.
1主动轴与中间轴的夹角必须等于从动轴与中间轴的夹角即31中间轴两端的叉面必须位于同一平面内
南京理工大学课程考试答案及评分标准
课程名称:
机械设计基础(I) 学分:3.0 大纲编号: 012241041 满分分值: 100 考试时间: 120 分钟
i46 =
z5 z6 =2 z 4 z 5′ z7 = 60 z 6′
∴ i17 = i14 i46 i6′7 = 40
(2)轮 7 的转向为顺时针方向. 3.解:在一个运动循环内,
Wd = M r
Wd 2π = ∫ M r d =
0 2π
1 × 2π × 400 2
i12 =
O2 P O1 P O2 P N 2 P = O1 P N 1 P

南京理工大学机械设计基础(下)答案1

南京理工大学机械设计基础(下)答案1

2）蜗杆右旋，蜗轮右旋 3）
第1页 共1页
三、 填空（每题 2 分） 1、小，大 2、深沟球轴承，80，圆锥滚子轴承，40 3、蜗轮上
四、 简答题
1、改进措施：1）加装风扇；2）增加散热片；3）蛇形冷却水管 （6 分） 2、 因为拧紧螺母后，螺栓初受到预紧力的作用外，还受到螺纹阻力矩的作用，使螺栓产生扭转切应力。
为了考虑扭转切应力对螺栓强度的影响，可将所受轴向预紧力增大 30%。（4 分） 3、—工作情况系数，考虑齿轮系统外部原因引起的附加动载荷对齿轮工作的影响。
140 100
1.4
e, X 2
0.41,Y
0.85
P1 X 1R1 Y1 A1 R1 200N
Pห้องสมุดไป่ตู้ X 2 R2 Y2 A2 0.41100 0.85 100 126N
4. 解：1 处：轴承定位高度超过内圈厚度；
2 处：轴段长应比轮毂稍短，且定位高度超过轴承内圈厚度；
3 处：圆螺母固定应有退刀槽。
— 动载荷系数，考虑齿轮副本身的误差引起的附加动载荷对齿轮工作的影响。
— 齿向载荷分布系数，考虑沿齿宽方向载荷分布不均的影响。
— 齿间载荷分布系数，考虑同时啮合的各对轮齿间载荷分配不均的影响。（4 分） 五、 设计计算题
1. 解：1）方向如图示
2. 解：1） 3 左旋，4 右旋
2） Ft1
2T1 d1t
2T1 mn z1 / cos
, Fr1
FT 1 cos
tg , Fa1
Ft1 tg
3）
3. 解：
S1 0.7R1 0.7 200 140N , S2 0.7R2 0.7 100 70N
A1 S1 , A2 S1

南京理工大学机械设计基础——链传动

南京理工大学机械设计基础——链传动

第八章 链传动
§8—1 概述
a
2 2
1 1

一、链传动工作原理与特点
优点:1)无弹性滑动和打滑,平均传动比恒定 2)张紧力小 3)效率高 4)可在恶劣环境下工作
缺点:1)瞬时传动比不恒定 2)传动平稳性差 3)有冲击和噪音 4)无过载保护作用
二、链传动的主要类型 按工作特性分：起重链，牵引链，传动链 传动链接形式分：滚子链；齿形链
齿顶圆直径 齿根圆直径
见表8-3
p d1
ha
r1 360°/z
da

二、链轮齿形 三圆弧一直线(凹齿形)
16A - 1×80 GB1243.1-83 80节 单排
链号16， p＝25.4
三、链轮的结构型式 １．实心链轮 ２．孔板式链轮 ３．组合式链轮
四、链轮的材料 要求：１）轮齿接触强度和耐磨性 ２）小链轮材料优于大链轮
16A 10A 12A
08A
24A 20A
28A 40A 36A 32A
小链轮转速n1 (r/min)
2、链轮齿数Z1、Z2及i
Z1过少— 1）传动不均性和动负荷增大
2）P增大后， 角增大，链绕进、出轮磨损加剧
3）当p一定时，z少，d小，圆周力（=2T/d）↑加 速轮与链的破坏
Z2过多—外壳尺寸大、重量加大； 节圆外移, 易脱链
③张紧不适当，松边垂度过大，起动、制动、反向、 突然卸载或超载必出现惯性冲击，增大了动负荷。
§8—6 链传动的受力分析
链传动中主要作用力有：
1、工作拉力 2、离心拉力
Fe 1000P V
Fc=qV2
3、垂度拉力（图８－１１）
Ff max Ff , Ff

南京理工大学机械设计基础(上)答案 (9)

南京理工大学机械设计基础(上)答案 (9)

(
)
B1 B0 B1 B2 10.3 = = = 1.745 Pb πm cos 20 3.14 × 2 × cos 20 (4)由于 ε α > 1 ,故可实现连续传动
(3) ε α = 2,左旋 由 d = mq ,得 q = d
m
= 12
BC1 AB
= 60 o
z3 90 = 1+ =6 z1 18
南京理工大学课程考试答案及评分标准
课程名称:
机械设计基础(Ⅰ) 学分: 2.0 教学大纲编号: 012241041 满分分值: 100 考试时间: 120 分钟 五,解:1, (1)由标准安装中心距 a = 试卷编号: 0122410409 考试方式: 闭卷 一,计算自由度 1,解:n=4 Pl=5 PH=0 所以 F=3n-2Pl-PH=3×4-2×5-0=2 2,解:n=4 Pl=5 PH=1 所以 F=3n-2Pl-PH=3×4-2×5-1=1 C 处有局部自由度 F 或 G 为虚约束 二,解:1,P12 为 A 点;P23 为 B 点;P34 为⊥BC 的无穷远处 P14 为 C 点;P13 为既在 AB 线上又在过 C 点⊥BC 的无穷远处, 因此 P13 在无穷远处;P24 为 AC 与 AB 的交点 A 2,P13 为 A 点;P23 为⊥CD 的无穷远处;P12 为 P 点 六,解:1.行星轮系 1-2-3-4, z 3 = 2 z 2 + z1 = 90 V2=VP=ω1lAP=10×10×0.01=1m/s. 三,解:ψ = 2 ar 60 o
K=
180 + θ =2 180 θ
z5 d = 5 = 2 z4 d4 ∴ i15 = i14 i45 = 12 n ∴ n5 = 1 = 100r / min (方向与 n 相反) i15 i45 =

南京理工大学机械设计基础上——解析法设计凸轮的轮廓曲线

南京理工大学机械设计基础上——解析法设计凸轮的轮廓曲线

§4—4 用解析法设计凸轮的轮廓曲线一、滚子从动件盘形凸轮1．理论轮廓曲线方程（1）直动从动件盘形凸轮机构图示偏置直动滚子从动件盘形凸轮机构。

求凸轮理论廓线的方程，反转法给整个机构一个绕凸轮轴心O 的公共角速度-ω，这时凸轮将固定不动，而从动件将沿-ω方向转过角度ϕ，滚子中心将位于B 点。

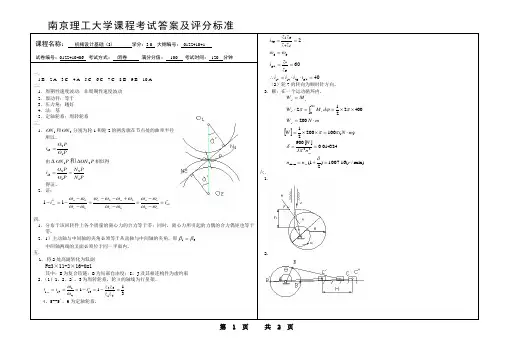
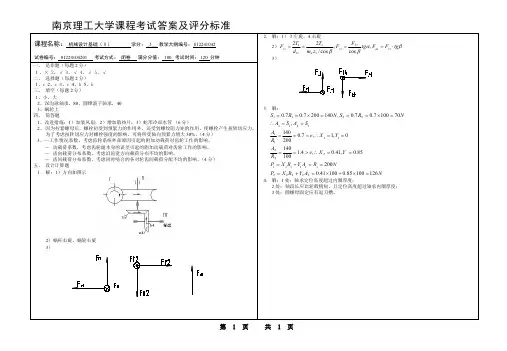
B 点的坐标，亦即理论廓线的方程为：⎭⎬⎫++=-+=ϕϕϕϕsin )(cos sin cos )(00s s e y e s s x （4-15） 220e r s a -=，r a 为理论廓线的基圆半径，对于对心从动件凸轮机构，因e=0，所以s 0=r a ⎭⎬⎫+=+=ϕϕs i n )(c o s )(s r y s r x a a （4-16） （2）摆动从动件盘形凸轮机构图所示为摆动滚子从动件盘形凸轮机构。

仍用反转法使凸轮固定不动，而从动件沿-ω方向转过角度ϕ，滚子中心将位于B 点。

B 点的坐标，亦即理论廓线的方程为：⎭⎬⎫-+-=-+-=)sin(sin )cos(cos 00ϕψψϕϕψψϕl a y l a x （4-17） ψ0为从动件的起始位置与轴心连线OA 0之间的夹角。

alr r l a T 2)(arccos 20220+-+=ψ （4-18） 在设计凸轮廓线时，通常e 、r 0、r T 、a 、l 等是已知的尺寸，而s 和ψ是ϕ的函数，它们分别由已选定的位移方程s =s (ϕ)和角位移方程ψ=ψ（ϕ）确定。

2．实际廓线方程滚子从动件盘形凸轮的实际廓线是圆心在理论廓线上的一族滚子圆的包络线。

由微分几何可知，包络线的方程为：⎪⎭⎪⎬⎫=∂∂=0),,(0),,(1111ϕϕϕy x f y x f （4-20） 式中x 1、y 1为凸轮实际廓线上点的直角坐标。

对于滚子从动件凸轮，由于产生包络线（即实际廓线）的曲线族是一族滚子圆，其圆心在理论廓线上，圆心的坐标由式（4-15）~（4-17）确定，所以由（4-20）有：0)()(),,(2212111=--+-=T r y y x x y x f ϕ0)(2)(2),,(1111=----=∂∂ϕϕϕϕd dy y y d dx x x y x f式（a ）和（b ）联立求解x 1和y 1，即得滚子从动件盘形凸轮的实际廓线参数方程： ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛±=221221//ϕϕϕϕϕϕd dy d dx d dx r y y d dy d dx d dy r x x T T （4-21） 上面的一组加减号表示一根外包络廓线，下面的一组加减号表示另一根内包络廓线。

机械设计基础 南理工11-12-14

机械设计基础 南理工11-12-14

按承载情况分
转轴——Shafts in bending(弯曲) and torsion(扭转).
心轴——Shafts in bending(弯曲) only.
自行车前轴属于哪种？
传动轴——Shafts in torsion(扭转) mainly。
Speed Reducer Drive Motor
轴承端盖与机座间加垫片 以调整轴的位置。
(7)锁紧挡圈、紧定螺钉或销 Set Screw, Pin 承载能力低，可同时兼做周向定位。
(8)圆锥面（+挡圈、螺母） Cone (+ retaining ring, nut ) 适于承受冲击和同心度要求较高的轴 端零件，可兼做周向定位。
2、零件的周向定位 Circumferential Fixing
对于转轴：已知支点(Point of support)，扭矩(Torque)、弯 矩(Bending Moment)可求. Take a helical gear shaft for example 1)Show the component forces that act in the vertical and Fr horizontal planes.
§11-2
The Configuration Design of Shafts
轴的结构设计
① 轴和轴上零件要有准确、牢固的工作位置。
② 轴上零件装拆、调整方便。 ③ 轴应具有良好的制造工艺性等。 ④ 尽量避免应力集中(Stress Concentration)。 一、拟定轴上零件的装配(assembly)方案 原则：1、轴的结构越简单越合理。 2、装配越简单、方便越合理。
Ft RH1 L2 C
Fa
a)

南京理工大学机械设计基础(上)试卷 (2)

南京理工大学机械设计基础(上)试卷 (2)

2、 证明一对渐开线直齿轮的传动比与两齿廓在节点处的曲率半径成反比。
五 、计算 1. 图示轮系中，设已知 z1 15 ， z 2 25 ， ' z 2 20 ， z 3 60 ，又 n1 200r / min ， n3 50r / min ，试求系杆 H 的转速 n H 的 大小和方向。
2. 在图示凸轮机构运动简图中，作出基圆，标出其基圆半径 r0 以及推杆的行程 H。
2 分） 1、构件所具有的 的数目称为自由度，作平面运动的自由构件具有 个 自由度。 2、瞬心是两个作平面相对运动刚体上瞬时 为零的 。 3、偏置曲柄滑块机构存在的几何条件为 。当以滑块为驱动件时，该机构存 在 位置。 4、凸轮机构从动件常用规律中，有刚性冲击的有 运动规律，而有柔性冲击 的有 。 5、两渐开线齿轮啮合传动时，当两轮的 略有改变时，两齿轮仍能保持 原 传动，此特性称为齿轮传动的可分性。 三 、简答（10 分） 1. 什么叫外啮合渐开线标准直齿轮的标准中心距 a？如何计算？ 2. 机构具有确定运动的条件是什么？
考试时间： 120 组卷教师：
宋梅利
审定教师：王华坤
一 、选择： （10 分） 1. 轮系运动时，各轮轴线位置固定不动的称为 A 、 周转轮系 ； B 、 定轴轮系 ； C 、 行星轮系 2. 在轴夹角β 固定的实用单万向联轴节中，当主动轴转过 360 时，从动轴的转角 A、小于 360°； B、等于 360°； C、大于 360° 3. 对于动平衡的回转件，则 A 、 一定是静平衡的； B 、 不一定是静平衡的； C 、必定不是静平衡的。 4.对于速比恒定的机构，在等效构件确定后，其等效转动惯量 A、与原动件的位置有关； B、与等效构件的角速度有关； C、与原动件的位置无关； 5. 当两渐开线齿轮的中心距略有改变时，该对齿轮的 A 、 传动比不变，且啮合角也不变； B 、 传动比有变化，但啮合角不变； C 、 传动比不变，但啮合角有变化。

南京理工大学机械设计基础上答案01224104105

南京理工大学机械设计基础上答案01224104105

α1 = α 2
VB1 cos α 1 = VC 3 cos α 2
Pb1 = Pb 2
∴ m1 cosα1 = m2 cosα 2
2．转动副是具有一个独立相对转动的运动副；移动副是沿一个方向独立相对移动的运动副。它们都是 平面低副，具有一个自由度。 四． 1．B´C´和转动副 B´、C´为虚约束。 因为构件 1 和 3 上 B´、C´两点间的距离保持恒定。 2．如图：为避免根切
∴ z min
五． 1．
mz sin 2 α 2 * 2ha = sin 2 α
．
第 1 页
共
1
页
ω 1l1 = ω 3 ⋅ 2l1 ω3 1 = ω1 2 M 3r ⋅ ω 1 = − M 3 ⋅ ω 3 ω M 3r = − M 3 3 = −50 N ⋅ m ω1
六．1． 2。
* ha m = r sin 2 α =
* ∴ ha m≤
mz sin 2 α 2
考试方式： 闭卷
1 z z 1− 2 3 z1 z ′ 2
(i ).
z 3 = 99,
i H 1 = 10000 i H 1 = −100
ψ 1 = ψ 3 ∴ AB // CD,
(ii ) z 3 = 100,
2．
d d 3． > 5; < 5 b b
4．允许；引起附加 5．基；曲率 三． 1．这两个齿轮的模数和压力角分别相等
南京理工大学课程考试答案及评分标准
课程名称：
机械设计基础（I） 学分：3.0 大纲编号： 012241041 满分分值： 100 考试时间： 120 分钟
iH 1 =
1 i1H
=
1 = H 1 − i13

南京理工大学机械设计基础上试卷01224104101

南京理工大学机械设计基础上试卷01224104101

组卷年月： 2002.04
组卷教师： 宋梅利
审定教师： 张庆
一、 下图是连杆机构的运动简图（μ l =0.001m/mm） 。 1 计算该机构的自由度； （8 分） 2 问该机构是否存在曲柄； （8 分） 3 若 AB 的角速度为 90rad/s，试用瞬心法求滑块 E 的速度。 （14 分） （指图示机构位置下滑块的速度）
1
八、 如图所示，已知轮系中各齿轮齿数。求传动比i 1H ；计算其自由度。 （15 分）
五、如下图左将机组的力和质量都换算到等效构件AB上， ，在机组稳定运转时，它的一个运动循环 对应于曲柄AB的转角ψ P =2π。 等效驱动力矩M d 为常数， 等效阻力矩Mr的变化如下图右所示。 设机组各构件的等效转动惯量J R =0.14kg m2 且为常数，ωm=25rad/s。若δ=0.04，试确定需装 在轴A上的飞轮转动惯量J F 。 （ 大纲编号： 012241041 课程名称： 机械设计基础（Ⅰ） 考试方式： 闭卷 考试时间： 120 学分： 3 分钟 试卷编号：01224104101 满分分值： 100
档案编号：
三、 两个相同的渐开线标准直齿圆柱齿轮，其压力角α=200，齿顶高系数h a *=1，在标准安装下传 动。若两轮齿顶圆正好通过对方的啮合极限点N，试求两轮理论上的齿数。 （16 分） 四、 用作图法设计一偏置直动尖底从动件盘形 凸轮机构的部分凸轮廓线：推程和远休止 程所对应的部分。已知凸轮以等角速度回 转，回转方向、从动件的初始位置及偏置 方式如图所示，e=10mm，r b =35mm，从动件在推程以等速上升，行程为h=30mm，升程角φ =150O，远休止角φ s =30O。 （16 分）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
人为的实物组合（不是天然形成的）； 人为的实物组合（不是天然形成的）； 各运动单元具有确定的相对运动； 各运动单元具有确定的相对运动； 必须能作有用功，完成物流、 必须能作有用功，完成物流、信息的传递及能 量的转换。 量的转换。 Machine(机器 is a mechanical system which 机器) 机器 can transmit (传递 or transform (转换 energy, 传递) 转换) 传递 转换 materials or information.
1.4 Purpose It is hoped that, after studying this textbook, the student will grasp(掌握 the basic theory and 掌握) 掌握 obtain the basic knowledge and skills(技能 技能) 技能 needed in mechanisms synthesis and kinematic and dynamic(动力学的 analysis of machinery. 动力学的) 动力学的 The knowledge to be obtained from this 基本的) textbook is therefore fundamental(基本的 in 基本的 analyzing existing(现有的 machines and 现有的) 现有的 designing new ones.
What is Machanism?
机构： 机构：具有机器的前两个特征
人为的实物组合（不是天然形成的）； 人为的实物组合（不是天然形成的）； 各运动单元具有确定的相对运动； 各运动单元具有确定的相对运动； Mechanism(机构 is a basic system of 机构) 机构 links(构件 which can transform(转换 or 构件) 转换) 构件 转换 transmit(传递 force and motion. 传递) 传递
锥齿轮减速器
圆柱齿轮减速器
自动控制部分——用于实现机器执行机构之间的工 用于实现机器执行机构之间的工 自动控制部分 作协调，或者各机器之间的工作协调。 作协调，或者各机器之间的工作协调。
1.2 Several Concepts About This Course 构件（ 构件（Link） ） 零件(Machine element) 零件 主动件(driving member)——输入构件 主动件 输入构件 从动件(driven member)——输出构件 从动件 输出构件 机架(frame) 机架
The Basis Course先修课程： 先修课程： 先修课程 Higher mathematics高等数学， physics普通物理， 高等数学， 普通物理， 高等数学 普通物理 mechanical drawing机械制图， rational 机械制图， 机械制图 mechanics理论力学， etc. 理论力学， 理论力学
主动件(driving member)——输入构件 主动件 输入构件 驱动力（或力矩） 驱动力（或力矩）所作用的构件 从动件(driven member)——输出构件 从动件 输出构件 随着原动构件的运动而运动的构件 机架(frame)——机构中相对不动的构件 机构中相对不动的构件 机架
1.3 Study Content（研究内容） （研究内容） 分析)and synthesis（综合）of Analysis (分析 分析 （综合） mechanisms—most content of the lesson 结构和运动学(kinematics) 结构和运动学( ) 机构的组成； ①机构的组成； 机构运动的可能性和确定性； ②机构运动的可能性和确定性； 分析运动规律。 ③分析运动规律。 动力学(kinetics dynamics) 动力学 运动的关系·F=ma 力——运动的关系 F=ma 运动的关系 功——能 能
Link构件 构件——运动单元体 构件 运动单元体 basic element in kinematics analysis
Machine element(零件 零件)—— a 零件 basic element（元素） of （元素） manufacture（制造）, e.g. （制造） coupler（连杆） body, nuts（螺 （连杆） （ 母）, bolts（螺栓） etc. . （螺栓） 构件可由一个或几个零件组成。 构件可由一个或几个零件组成。 机构：能实现预期的机械运动的各 机构： 构件（包括机架）的基本组合体。 构件（包括机架）的基本组合体。
Mechanisms and Machine Theory
(机械原理)
School of Mechanical Engineering, NUST
Meili Song
作业公共邮箱： 作业公共邮箱： jigong07015001@ 密码： 密码：206206
本课程的教学环节
1.课堂讲授 2.一般作业 3.基本实验（3个） 1) 机构运动简图的测绘； 2) 机构运动参数测定； 3) 刚性回转件的动平衡。 4.综合训练环节（撰写小论文） 5.课堂小测验； 6.网上交流与答疑
1. Cylinder 缸体 or Frame 机架 2. Prank 曲柄 4’. Pinion 小齿轮 4”. Flywheel飞轮 飞轮 5. Gear 大齿轮 5’. Inlet cam进气凸轮 进气凸轮 5”.Outlet cam排气凸轮 排气凸轮 6. Inlet valve进气阀 进气阀 7. Outlet valve排气阀 排气阀
工作机—working machine：能完成机械预期的动 ： 如机器人的手爪、 作，如机器人的手爪、起重机等
该机器人的手爪协调 运动夹持球体实现任 意运动， 意运动，这是一种智 能型机器人。 能型机器人。
传动部分——transmission system：把原动机的 把原动机的 运动和功率传递给工作机的中间环节
机械原理课程参考书目
机械设计基础（ 王华坤 范元勋 机械设计基础（上） 兵器工业出 版社 机械原理》 郑文纬，吴克坚，高等教育出版社。 《机械原理》，郑文纬，吴克坚，高等教育出版社。 机械原理习题集》 南京理工大学印制。 《机械原理习题集》，南京理工大学印制。 Mechanisms And Machine Theory / Ye Zhonghe & Lan Zhaohui & M.R.Smith «Mechanisms and Dynamic of Machinenery», Hamilton H.Mahie, Fred W.Ocvirk,1987
Examples of Mechanism Slider-crank Gear mechanism mechanism 曲柄滑块机构 齿轮机构
1
2
Cam mechanism 凸轮机构
1 6
5
3 4
1
4'
5'
Composition(组成 of machine 组成) 组成 一台典型的现代化机器是由四个部分组成的，即 一台典型的现代化机器是由四个部分组成的， 原动机、传动机构、执行机构和控制系统。 原动机、传动机构、执行机构和控制系统。 原动机-prime mover：机械动力的来源，如内燃 机械动力的来源， 机械动力的来源 蒸气机、 机、蒸气机、电动机等
1.1 Study Object(研究对象 研究对象) 研究对象 1.2 Several Concepts About This Course 1.3 Study Content（研究内容） （研究内容） 1.4 Purpose（目的） （目的）
1.1 Study Object: Machinery(机械 机械)—— 机械 Machine（机器） and Mechanism(机构 机构): （机器） 机构 Machine（机器） （机器） Mechanism(机构 机构) 机构
Chapter1 Introduction Chapter2 Structural Analysis of Planar Mechanisms Chapter3 Kinematic Analysis of Mechanisms Chapter4 Planar Linkage Mechanisms Chapter 5 Cam Mechanisms Chapter 6 Gear Mechanisms Chapter 7 Gear Trains Chapter 8 Other Mechanisms in Common Use Chapter 9 Balancing of Machinery Chapter 10 Motion of Mechanical Systems and Its Regulation Chapter 11 Efficiency of Machine
主旋翼
尾 旋 翼
美国西科斯基公司生产的“黑鹰” 美国西科斯基公司生产的“黑鹰”直升机
“神舟五号”发射时的情景。发射塔、 神舟五号”发射时的情景。发射塔、 神舟五号 运载火箭都是庞大的机器。 都是庞大的机器 运载火箭都是庞大的机器。
What is Machine?
机器（三个特征）： 机器（三个特征）：
Attentions （本章重点） 本章重点）
Several concepts：机器、机构、构件、 ：机器、机构、构件、 零件、机架、原动件、 零件、机架、原动件、从动件
Homework
Read book p1-3.
撰写小论文基本要求
1、题目 、 机械工程发展史、机器人发展史、微型机器人发展史、 机械工程发展史、机器人发展史、微型机器人发展史、 机械原理发展史、智能机械发展史、航天器发展史、 机械原理发展史、智能机械发展史、航天器发展史、航 空器发展史、微型机械发展史等，机械在某一领域（ 空器发展史、微型机械发展史等，机械在某一领域（如 国防、医疗等）的应用和发展，或自选此类主题。 国防、医疗等）的应用和发展，或自选此类主题。 2、要求 、 (1) 通过大量文献的查阅和综述，对相关领域的发展历 通过大量文献的查阅和综述， 现状和趋势有一个深入了解，开阔思路， 史、现状和趋势有一个深入了解，开阔思路，增加课 程学习的目的性和主动性； 程学习的目的性和主动性； (2)着重培养大家的文献调研和总结能力，应查阅大量 着重培养大家的文献调研和总结能力， 着重培养大家的文献调研和总结能力 文章和资料，不允许对文献进行长篇拷贝； 文章和资料，不允许对文献进行长篇拷贝；