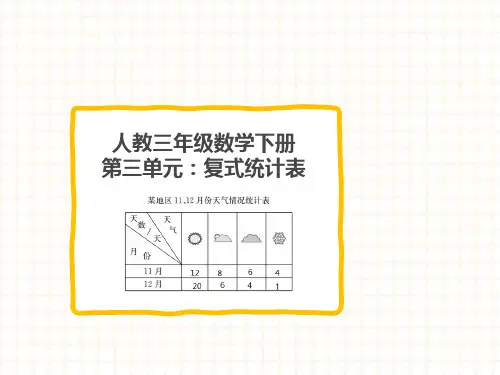
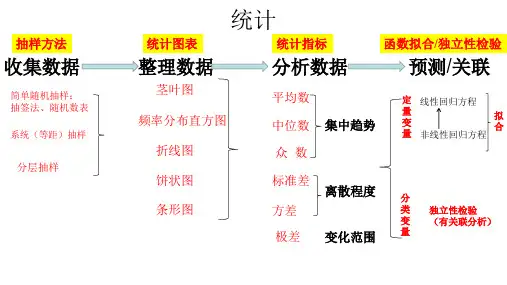
统计思维导图学习资料

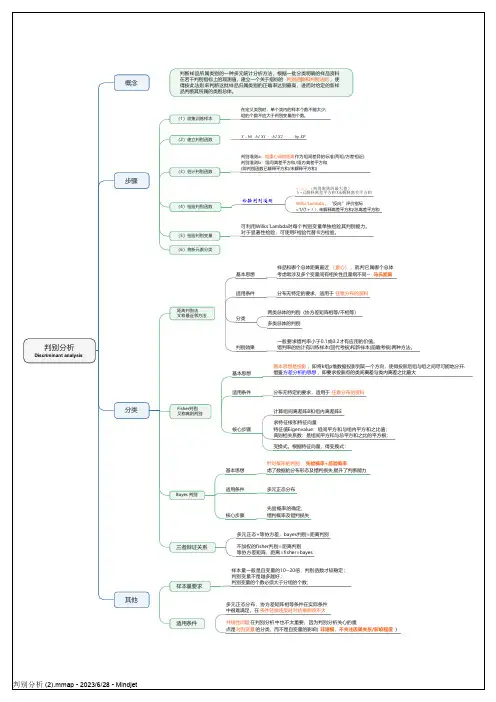
判别分析Discriminant analysis 概念判断样品所属类别的一种多元统计分析方法，根据一批分类明确的样品资料在若干判别指标上的观测值，建立一个关于指标的判别函数和判别法则，使得按此法则来判断这批样品归属类别的正确率达到最高，进而对给定的新样品判断其所属的类别总体。

步骤（1）收集训练样本在定义类别时，单个类内的样本个数不能太少;组的个数不应大于判别变量的个数。

（2）建立判别函数Y b0b1 X1b2 X2bp XP（3）估计判别函数判别准则a：组重心间的距离作为组间差异的标准(两组/方差相近）判别准则b：组间离差平方和/组内离差平方和(即判别函数已解释平方和/未解释平方和)（4）检验判别函数检验判别准则（判别准则的最大值）λ=已解释离差平方和/未解释离差平方和Wilks'Lambda，“反向”评价指标=1/(1+λ),未解释离差平方和/总离差平方和（5）检验判别变量可利用Wilks'Lambda对每个判别变量单独检验其判别能力。

对于显著性检验，可使用F检验代替卡方检验。

（6）将新元素分类分类距离判别法又称最近邻方法基本思想样品和哪个总体距离最近（重心），就判它属哪个总体考虑常涉及多个变量间有相关性且量纲不同--马氏距离适用条件分布无特定的要求，适用于任意分布的资料分类两类总体的判别（协方差矩阵相等/不相等）多类总体的判别判别效果一般要求错判率小于0.1或0.2才有应用的价值。

错判率的估计有训练样本(回代考核)和新样本(前瞻考核)两种方法。

Fisher判别又称典则判别基本思想基本思想是投影，即将k组p维数据投影到某一个方向，使得投影后组与组之间尽可能地分开.借鉴方差分析的思想，即要求投影点的类间离差与类内离差之比最大适用条件分布无特定的要求，适用于任意分布的资料核心步骤计算组间离差阵B和组内离差阵E求特征根和特征向量特征值Eigenvalue：组间平方和与组内平方和之比值；典则相关系数：是组间平方和与总平方和之比的平方根；变换式。

第7讲 条形统计图（思维导图+学问梳理+例题精讲+易错专练）一、思维导图二、学问点梳理学问点一：条形统计图条形统计图能清楚地表示每个项目的具体数据，易于比较出每个项目的数据之间的多少。

要点提示：条形统计图的优点是能直观地看出数据的多少。

直条越长，所表示的数据越大，直条越短，所表示的数据越小。

统计数据时，有时可以一格表示1个单位，假如数据较大，可以用1格表示多个单位，这样绘图、读图都比较简便。

学问点二：制作条形统计图制作条形统计图，直条的高度要和纵轴上的数字一一对应，直条与直条的间隔要均等。

条形统计图分为纵向和横向，横向条形统计图，适用于项目较多，数据不大的状况；竖向条形统计图，适用于项目较少，数据较大的状况。

留意：横向和纵向，原理一样，只是方向不一样。

三、例题精讲考点一：1格表示一个单位的条形统计图【典型一】聪聪制作了一幅统计图，下面选项（ ）有可能是这幅统计图的标题。

条形统计图A．5个班考试得满分的人数B．3个同学收集塑料瓶的数量C．杭州6～10月的月平均气温D．某学校周一～周五的同学人数【分析】观看这幅统计图可知：有5个直条，表示的数据分别是7、6、9、8、10，据此进行分析每个选项。

【详解】A．5个班考试得满分的人数分别是7个、6个、9个、8个、10个，符合题意；B．3个同学收集塑料瓶的数量，只需要3个直线，不符合题意；C．杭州6～10月的月平均气温，气温的单位摄氏度，依据生活常识以及数据特点，不符合题意；D．某学校周一～周五的同学人数，一个学校的人数不行能只有7个、6个、9个、8个、10个，不符合题意。

故答案为：A【点睛】此题考查的目的是理解把握条形统计图的特点及作用。

【典型二】下图是幼儿园购买水果状况统计图。

（1）这是一幅条形统计图，图中1格表示( )千克水果。

（2）购买最多的水果是( )。

（3）假如1千克苹果2.5元，幼儿园买这些苹果一共要( )元。

【分析】（1）观看这个条形统计图可知，1格表示1千克。

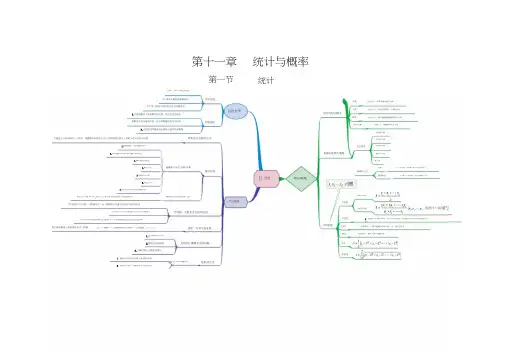
第十一章 第一节统计与概率统计他们都是衡量一组数据波动大小的量 学习误区分不清集中趋势和离散趋势 总体弄不清三种统计图的表达意义的侧重点 个体总结升华统计的相关概念样本知能提升 样本容量扇形统计图样本估计总体的方法 条形统计图统计图表折线统计图数据的收集与整理频率分布图3.确定组距与组数; 直方图画频率分布直方图的步骤 普查 调查的方式画统计图抽样调查从总体中，抽取部分个体进行调查的方式统计 知识梳理//算数平均数画频数分布折线图的方法 学法指导平均数覘養i •踽矿加权平均数众数的大小只与数据中的部分数据有关 中位数分析数据众数 极差利用统计量解决实际问题 方差标准差数形结合法极差、方差与标准差 为了一定的目的，对考察对象进行全面的调查在统计中，所提取的样本个数平均数的大小与每一个数据有关，任一数据的变动都会引起平均数的变动取直方图中每个矩形上边的中点，把这些点用线段依次连接起来即可 在统计中，所有考察对象的全体在统计中，组成总体的每一个考察对象即通过从总体中抽取一个样本，根据样本的情况去估计总体的相应情况，常用于设计实际应用题 中位数只与数据的排列位置有关，某些数据的变动对它没有影响3.对事件提出合理化的建议这三个量越小，这组数据的波动越小，也越稳定；反之亦然 理解各个统计量的作用，使分析数据更具有方向性 5.列频率分布表;在统计中，实际观测或调查的那部分个体平均数、众数和中位数的区别一组数据中，最大与最小数据的差7.写出统计图的名称和数据来源 4.确定分点 6.画直方图 3.注意题目的侧重点来选取合适的知识解题 2.植物长势的判断 2.计算数据中的最大值与最小值的极差（2）根据已知条件，绘制或补全各类统计图n 个数据按大小顺序排列，处于中间位置的一个数据（或中间两个数据的平均数）1.认真理解各个基本概念的实质，找出区别与联系 （1）观察分析各类统计图表，解决相关问题1.比赛成绩的评估 1.收集数据；（放到统计图内）一组数据中，出现次数最多的那个数（注：有时会有多个）■s 常见的命题形式总体、样本的概念混乱。

统计与可能性思维导图六年级
了解思维导图的朋友，总会被它对称的 ️状束缚！作为一种思维的可视化工具，㴯怎样更好的表达思维才是最关键的。

思维导图似乎很容易被模仿，因为它的绘制技巧实在太简单了，对结构布局和线条字体的要求，一看便知。

但是，如果真的希望利用思维导图来提高学习效率，只有将这一强大的思维工具和具体的学科学习相结合！在具体学科学习中应用思维导图至少有两大难点，关键词的提炼和知识间联系的建立。

前者需要学习者有极强的概括能力，后者则要求对知识有高位的整体思考，总的来说，都是需要有自己的理解和体会！在此基础上，才有个性化和创造性！以下分享的是初中数学统计与概率知识的思维导图，全班共45人，交回44人，完成时间是上周一到五，这届孩子是从初一到初三陆续学习，应用思维导图，本次作业没有做任何指导，只是要求通读七八九年级统计与概率部分的章节，用自己的方式呈现知识结构。

从作业中，我们看到了不同的风格。

有的侧重于结构，提炼了一些关键词。

有的侧重于知识的复习，不仅有知识点还有相应的例子。

有的突出本质，没有过多的在色彩上下功夫。

有的则图文并茂，带来一种美的享受！总之，相信孩子们在绘制的过程中，都有丰富的思维经历和情感体验，在此，我们并不做任何对比，因为并没有一个恰当的标准可以衡量每一个孩子的这段经历！为每一个孩子点赞 ️……另，排列顺序按交过来的顺序，随机拍摄，没有特别含义！。

四年级数学上册统计与概率的思维导图
统计与概率是四年级数学中的重要知识点，下面我们就从思维导图来谈一谈统计与概率。

思维导图包括以下内容：统计主要有调查、汇总和分析三个维度；概率有四个概念——事件、改变可能性表示成比例、概率求解及概率比较；另外还有一个分类手段——概率分析图。

首先，调查是统计中的重要内容，它涉及到调查对象、调查数据、收集方式等问题。

至于汇总，则涉及到分类表、频率表、饼图、面积图等形式。

最后，分析则是对调查汇总数据进行分析，采用不同形式并对数据有准确描述，如平均数、中位数、众数等。

在概率方面，先要弄清概念事件、改变可能性表示成比例、概率求解及概率比较四个概念，之后，从不同的概率的角度进行把握，采用表格、计算公式、概率分析图三种方式具体表现出来。

通过上述思维导图，我们对四年级数学上册的统计与概率的知识有了进一步的认识，四年级数学的知识变得更加清晰，引导学生从概念层面入手，掌握它们之间的联系，增强理解能力，掌握统计与概率有效把握它们的规律。