16.1.2分式的基本性质通分导学案3

格式：doc
大小：74.00 KB
文档页数：2

下载文档原格式

16.1.2(2)分式基本性质2节

分式的基本性质第三课时通分
复习引课
探究新课
计算
（1）1/2+1/3=
（2）3/4+5/6=
那我们学的分式是否也可以像分数一样通过通分进而计算呢？
一、尝试解决
二、请同学们自主学习课本第7页，寻找最简公分母
三、探究分式通分的步骤：
思考的问题：
（1）分式通分的意义是什么？分式通分的根据是什么？分式通分时应特别注意什么？
教材9页7题通分
今天我的收获是————————————————————
16．1.2（2）通分
什么事通分？最简公分母？
例题讲解
（1）
（2）
（2）
自主完成
△巩固新知
□分式分子分母是单项式的通分公分母好确定，而分子分母是多项式的公分母需先分解因式后再通分学生掌握的不好
总体要求：1.“统一”设计“分段”教学；2.围绕“三维”落实“三问”；3.充实“心案”活化“形案”。
（2）分式通分的关键是什么？如何确定几个分式的最简公分母？
（3）通分与约分有何区别
例1通分
（1）
（2）
（2）
学生解答
阅读教材，小组合作交流
学生交流后师生共同归纳
学生自己做完以上各题后，以小组为单位进行交流，沟通，及时发现问题，解决问题
△以小学学过的旧知引课，从而过渡到今天的新知
通过小组讨论交流得出出最简公分母的概念
教教师活动
学生活动
△设计意图
◇资源准备
□评价○反思
小结
1．通分：
（1）和（2）和
2．通分：
（1）和（2）和
（3）和（4）和
学生小结心得
学生板前做，师评

16.1.2分式的基本性质

A B A B A M （M 0） BM AM （M 0） BM
分数的基本性质：分数的分子分母都乘以（或除以）同一个不等于零的数，分数的值不变.
下列各组分式，能否由左边变形为右边？ 2 a(a b) (2) x 与 x( x 1) a (1) 与 2 ab a b 3y 3 y( x 1) x xa xy y (3) 与 (4) 2 与 y ya x x
1 , (3) x² － y²
1 x² ＋xy
(x＋y)(x－y) ∵ x² － y² ＝____________, x² ＋xy＝__________, x (x ＋ y )先把 Nhomakorabea母分解因式
1 1 ∴ 与的最简公分母为____________, x(x＋y)(x－y) x² － y² x² ＋xy xx 1 x ³ － xy x (x ＋ y)( x² － y) 因此＝________________, x² － y² x－y x 1 x³ － xy ² y) x (x ＋ y)( x－＝ ________________, x² ＋xy
约分：
3 6
1 1 通分：和 2 3
4、分数的基本性质是什么？
分数的基本性质：分数的分子分母都乘以（或除以）同一个不等于零的数，分数的值不变。
a 分式 2 a
分式 n
2
1 （a≠0)与 2 相等吗？
（n≠0)与
说说你的理由。
mn
n 相等吗？ m
分式的基本性质：
分式的分子与分母都乘以（或除以）同一个不等于零的整式，分式的值不变.
2x(x＋2) (x－2)
就是这两个分式的最简公分母.
a b c , 2 , (3)分式 2 a 4a 4 4a 8a 4 3a 6

16.1.2分式的基本性质学案

东辛店中学人教版初中数学八年级教学案
课题
16.1.2分式的基本性质
课时
第1课时
课型
新授
主备人
王金涛
学习目标
1．理解分式的基本性质.
2．会用分式的基本性质将分式变形.
学习重点
理解分式的基本性质.
学习难点
灵活应用分式的基本性质将分式变形。
学习过程
一情境导入
1.[思考]：下列两式成立吗？为什么？
2.一般地，对于任意一个分数有：
四．课堂小结
这节课你有什么收获，请你 (2) =
（3) = (4) =
2．判断下列约分是否正确：
（1） = （2） = （3） =0
3．约分：（1）（2）（3）
4．通分：
（1）和（2）和（3）
5.应用提高：不改变分式的值，使下列分式的分子、分母不含“－”号：
（1）（2）（3）
6.在化简分式时，小颖和小明的做法出现了分歧：
小颖：
小明：
你对他们俩的解法有何看法？说说看！
学生感悟
(教师修订)
3.
为什么？
二、探究新知
活动1分式的基本性质
1.类比分数的基本性质，你能想到分式的基本性质吗？（试着用自己的语言叙述）
2.分式的基本性质
分式的分子与分母同乘（或除以），分式的值.
可用式子表示为：＝＝（C≠0）
其中A,B,C是整式。
3.应用填空
（1） =
分析：依据分式的基本性质（1）看分母如何变化，想分子如何变化。
（2）看分子如何变化，想分母如何变化。
活动2通分和约分
1.联想分数的通分和约分，有例1你能想出如何对分式进行通分和约分吗？

分式的基本性质---通分导学案3

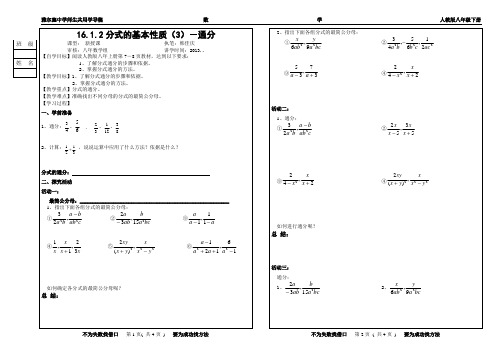
学生自主学习学案审核人：科目初二数学课题分式的基本性质--通分授课时间月日设计人班级八姓名序号 3 学习目标 1. 理解并掌握分式的基本性质及最简公分母的含义； 2.灵活运用分式基本性质将分式通分变形。

重难点会求分式的最简公分母，灵活运用分式基本性质将分式通分。

【学习过程】一、独立看书4页:(10分钟）二、独立完成下列预习作业：1、利用分式的基本性质，将分式的分子和分母同乘适当的整式，不改变分式的值，使几个分式化为分母相同的分式，这样的分式变形叫做分式的 .2、根据你的预习和理解找出：①x 1与y3的最简公分母是； ②a x 与ab y 的最简公分母是； ③ab b a +与22a b a -最简公分母是；④231yz x 与22xy 的最简公分母是 . 如何确定最简公分母？三、合作交流，解决问题：1、通分：⑴b a 223与cab b a 2- ⑵26x ab ，29y a bc2、通分：⑴52-x x 与53+x x ； ★⑵2121a a a -++，261a -．解： =b a 223 =-cab b a 2 =-52x x =+53x x 解：四、巩固提高：1、分式223ab c 和28bc a -的最简公分母是 . 分式11-y 和11+y 的最简公分母是 . ★2、化简：._______44422=++-a a a 3、化简分式2b ab b +的结果为（） A 、b a +1 B 、b a 11+ C 、21b a + D 、b ab +1 ★4、若分式的分子、分母中的x 与y 同时扩大2倍，则分式的值（） A 、扩大2倍 B 、缩小2倍 C 、不变 D 、是原来的2倍 ★5、不改变分式的值，使分式的各项系数化为整数，分子、分母应乘以（） A 、10 B 、9 C 、45 D 、90 ★6、不改变分式3253232-+-+-x x x x 的值，使分子、分母最高次项的系数为整数，正确的是（） A 、3252322-+++x x x x B 、3252322-++-x x x x C 、3252322+--+x x x x D 、3252322+---x x x x 7、通分：⑴bd c 2与243b ac ★⑵2)(2y x xy +与22yx x -⑶bca y ab x 229,6 ★⑷16,12122-++-a a a ay x y x 913110151+- )0,0(≠≠+y x yx xy。

人教版数学八年级上册15.1.2分式的基本性质(3)-通分(教案)

-掌握通分的步骤与方法：包括找出分式的最小公倍数作为新的分母，然后分别对分子和分母进行等比例扩大，实现分式的通分。重点讲解如何寻找最小公倍数及其在通分中的应用。
-运用通分解决实际问题：将通分应用于解决具体的数学问题，如分数比较大小、分式加减运算等，强调通分在实际计算中的重要性。
举例：比较两个分式$\frac{2}{3}$和$\frac{5}{4}$的大小，需要先通分，将它们转化为同分母的分式，如$\frac{8}{12}$和$\frac{15}{12}$，从而直观地判断大小。
本节课，我们将学习分式的通分，掌握通分的步骤，并通过实例练习，使同学们能够熟练运用通分解决分式加减的问题。
二、核心素养目标
1.培养学生的逻辑推理能力，通过分式通分的探究，理解数学知识之间的内在联系，提高解决问题的逻辑思维。
2.培养学生的数学运算能力，掌握通分的具体方法，灵活运用到分式的加减运算中，提升运算速度和准确度。
3.培养学生的数学建模能力，将现实生活中的问题转化为分式计算问题，通过通分解决实际问题，增强数学应用意识。
4.培养学生的数学抽象能力，从具体的分式实例中提炼出通分的概念和性质，体会数学抽象的过程，提高数学素养。
三、教学难点与重母不同的分式化为分母相同的分式，以便进行加减运算。这是本节课的核心内容，教师需通过直观的图示和实际例题，让学生深刻理解通分的意义和作用。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《分式的基本性质（3）-通分》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要将不同分母的分数进行比较或运算的情况？”（如购物时比较不同规格商品的价格）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索通分的奥秘。

16.1.2分式的基本性质(3)-通分

a b ab
a
b
a 1 , a 1 1 a
2、
a 1 6 , 2 a 2a 1 a 1
2
3、 5 x 20 , x 2 9 x 20 , 5 x
x5
5
x
活动五： 1、分式 x 2 ， 2 x 3 ，
( x 1) 2
(1 x )3
5 的最简公分母（ x 1
要为成功找方法
雅尔塞中学师生共用学导稿 3、
数 4、 a 3 , a 3
学四、学习体会
人教版八年级下册
3 5 1 , 2 , 2 4a b 6b c 2ac 2
5
7
5、 x , x 1 , 3x
1
x
2
五、课后拓展
活动四：通分： 1、
b a 已知 1 1 1 ，求的值。
（6） x 2 x , x 2 x
2
1
3、已知 x y z ，求 xy yz xz 的值。 2 3页 )
要为成功找方法
不为失败找借口
第6页 ( 共4页 )
要为成功找方法
2、计算： 1 1 ，说说运算中应用了什么方法？依据是什么？
2 3
分式的通分：二、探究活动活动一：最简公分母：__________________________________________________________ 1、指出下面各组分式的最简公分母： ①
③ 4 x2 , x 2
2
x
④ ( x y) 2 , x 2 y 2
2 xy
x
3 ab , 2a 2 b ab 2 c
1 x 2 , , x x 1 3x

八年级数学《分式的约分和通分》教案

“三部五环”教学模式设计《16.1.2分式的基本性质（2）》教学设计
活动三变式训练，巩固新知题组一：选择题
1、下列说法错误的是（） A ．
a 21与24a b
通分后分别为242a a 与2
4a
b B ．
z xy 231与y
x 2
31
通分后分别为z y x x 223与z
y x yz
2
23 C ．
n m +1与m
n -1
的最简公分母为2
2
n m - D ．
)(1n m a -与m
n -1
最简公分
母为))((m n n m a -- 2、下列约分正确的是（） A ．
33
=+m
m B.
022=--y x y x C.
b
a
b x a x =++ D.
1-=-+-y x y x 题组二：快速解答 1、约分
2、通分（1）
2
261
21xy
y x -与（2）
6
4312---+x x x
x 与题组三：挑战自我
【师生活动】
教师相机出示题组，其中题组一口答，题组二、三纸笔演练
（题组二的1题分组练习，交叉评价），生思考并独立完成，
教师巡视指导，相机提名板演，重点关注学困生的表现，
及时辅导、补救。

【设计意图】
培养学生自主学习的思想，观察其成效
板书设计
16.1.2分式的约分和通分（2）。

16.1.2 分式的基本性质

0.01x 5 ⑵ 0.6a 5 b ⑴ 3 0.3 x 0.04 2
0 .7 a
5 1 x y 5 , (3) 6 5 1 x y 6 5
5bΒιβλιοθήκη 例5：约分- 25a bc 5abc 5ac 5ac （） 1 2 15ab c 5abc 3b 3b
2 3 2 2
x2 9 x 3x 3 x 3 （2） 2 2 x 6x 9 x3 x 3
xy 2.若把分式中的 x 和 x y
的值(
y
都扩大3倍,那么分式
A
).
A．扩大3倍 C．扩大4倍
B．扩大9倍 D．不变
1 1 2a 3ab 2b 已知， 3 ，求分式的值。 a b a ab b
3x 3xy x y 2 6x ( 2x )
2
例3：不改变分式的值，使下列分子与分母都不含“－”号
2x 2x ⑴ 5y 5y
3a 3 a ⑵ 7b 7b 10 m 10 m ⑶ 3n 3n
例4：不改变分式的值，把下列各式的分子与分母的各项系数都化为整数.
x x x (2) 2 3 y( x 1) 3 y
3
将左边分式的分子与分母都除以 ( x 1)
2
例2
填空
ab (1) 2 ab ab
2
(a ab)
2a b ( 2ab b ) , (b 0) 2 2 a ab
2
x ( 1 ) (2) 2 , x 2x x 2
a b a b 2a 2a 2 2ab 2 2 2 2 ab c ab c 2a 2a b c
2x 3x （2）与 x5 x5

分式的基本性质教案

通过具体例子，引导学生回忆前面学段学过的分数约分、通分的依据-----分数的基本性质，再用类比的方法得出分式的基本性质.在这个活动中，首先激活了学生原有的知识，体现了学生的学习是在原有知识的基础上自我生成的过程.
问题与情境活动 2 问题（1）类比分数的基本性质，你能想出分式有什么性质吗？
（2）应用分式的基本性质时需要注意什么？
学生归纳出以下要点： ① 分子、分母应同时做乘、除法中的同一种变换； ②所乘（或除以）的必须是同一个整式； ③所乘（或除以）的整式应该不等于零. 在活动中教师要注意：（1）学生能否用数学语言表述新知识；（2）学生对“性质”的运用注意事项是否理解.
师生行为
设计意图
教师提出问题学生思考、讨论后在全班交流. 分式的分子与分母都乘（或除以）同一个不等于 0 的整式，分式的值不变.这个性质叫做分式的基本性质.用式子表示为：
A A•C A A÷C = ， = B B•C B B ÷C
其中 A,B,C 是整式.
教师引导学生用语言和式子表示分式的基本性质，这是学生运用类比的方法可以做到的.在这一活动中，学生的知识不是从老师那里直接复制或灌输到头脑中来的，而是让学生自己去类比发现，即让学生自己经历发现结论的过程，并总结出结论，从而实现学生主动参与、探索新知识的目的.
问题与情境活动 6 教学反思
师生行为这节新授课的设计，目的是让学生学会学习，学会思考，学会创造，进而培养学生用数学的思想方法，思考并解决实际生活中所遇到的各种问题，这也是学生适应未来生活必须的基本素质。
设计意图对本节课教学效果的评价.
教学过程设计

16.1.2分式的基本性质-通分导学案

15.1.2分式的基本性质---通分班级：姓名：学习目标：1、经历用类比、观察、联想的方法探索分式通分的方法的过程，理解通分与最简公分母的意义.2、能正确熟练地运用分式的基本性质将分式通分.课前回顾：约分(1)1616822-+-a a a （2）ba b a +---2 （2）y x y x -+--32 学习过程：一、自学探究1、回顾：将异分母分数854123，，化成同分母分数为._____85____,41___,23=== 2、分数的通分是：把分母的分数化成分母的分数叫做分数的通分。

其根据是。

3、启发：分式的通分与分数的通分类似，那么什么是分式的通分呢？其根据又是什么？4、尝试概括：分式通分的定义：。

分式的通分的根据是5、最简公分母：(1)分式ba x abc a 22,,b 的最简公分母是 ; 22,y x y y x x --的最简公分母是 .22222,2,,bab a b a b ab a b a b a b b a a +-+++--+的最简公分母是 . (2)请概括最简公分母：最简公分母的系数是各分母的系数的 , 字母取各分母所有因式的的积。

二、新知运用:1、指出下列各组分式的最简公分母. （1）；（2）；（3）.2、举例：例1、通分： ().5352)2(,2a 3122+--x x x x c ab b a b 与与解：（1）最简公分母是 . =b 22a 3 = cab b a 2-= = （2）最简公分母是 . =-52x x = =+53x x =3、巩固练习：通分： (1),43bd 2c 2bac 与；（2) (3) ;)(2222y x x y x xy -+与(4) (5) (6)xx x 26912--与三、知识总结：1、分式的通分是： . 分式的通分的根据是: .2、分式的最简公分母是：四、当堂检测：1、判断下列通分是否正确：解：∵ 最简公分母是∴ ,2、填空：（1）将通分后的结果是；（2）分式与的最简公分母是__________。

分式的基本性质(3)通分_教案

15.1.2 分式的基本性质（3）----通分教学设计教学目标1．进一步理解分式的基本性质.2．学习掌握分式的约分和通分．3．通过学习分式的基本性质，约分、通分法则，渗透类比的思想方法.教学重点掌握通分的法则教学难点运用分式的基本性质，将分式进行变形教学过程设计一、复习回顾二、复习引入1.分数的通分计算解：(1)(2)变形的依据是分式的基本性质，重点是求出分母的最小公倍数。

分数的通分：根据分数的基本性质，把几个异分母的分数分别化成与原来的分数相等的同分母的分数。

师生活动：教师指出(1)是约分，依据是分式的基本性质，那么(2)是什么变形呢？从而引入新课。

2.分数通分的知识梳理根据分数的基本性质，把几个异分母的分数分别化成与原来的分数相等的同分母的分数，叫分数的通分.1.通分的依据是：分数的基本性质2.通分的基本方法是：先找出分数的分子、分母的最小公倍数,再通分.3.通分的目的：化为同分母分数设计意图：从学生熟悉的分数通分入手，回顾分数的计算及知识梳理，自然衔接新课。

三、类比归纳，讲授新课观察课前的填空题：教师指出是各分母的最简公分母；并得到分式通分的概念：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同2 2 2分母的分式，叫做分式的通分。

我们把各分母的所有因式的最高次幂的积，叫做最简公分母.探究：如何确定最简公分吗1.定系数：各分母系数的最小公倍数2.定字母：各分母中含有的所有字母3.定指数：各字母最高次幂设计意图：通过分数概念的类比，学生能轻松得出分式的概念，并进行类比记忆。

通过事例探究如何确定最简公分母。

例4.解：最简公分母是2a2b2c.师生活动：教师给出例题的示范，并指出由分母的变化决定分子的变化。

跟踪训练1通分：最简公分母是解：最简公分母是(x+5)(x-5).教师总结：分母是多项式时，先因式分解，再将每一个因式看成一个整体，最后确定最简公分母．跟踪训练2通分：解：最简公分母是(a+b)(a-b).跟踪训练3跟踪训练4找出各组分式的最简公分母师生活动：请学生到白板上板演，教师巡视并答疑解惑。

16.1.2分式的基本性质3

C. 12xy2
D. 12x 2 y 2 。
1 x , 最简公分母是 x x 2( x 1)
(1)
B 综合训练题： 1 1 通分：与 2 2 4x 2x x 4
3 mn 与 2 2 2m n m n p
(2)
2x 3x 与 x 25 2 x 10
2
七、学习反思：
师生活动：
四、训练案： A 基础训练题： 2 xy x 通分：与 2 2 （x y） x y2
五、当堂检测: 1.三个分式 A. 4 xy 2.分式 3.通分：
2
六、作业布置: ）。
教材 9 页第 7 题。
y x 1 , 2, 的最简公分母是（ 2 x 3 y 4 xy
B. 3y 2
1 x 例：通分：（1）x 2 4 与 4 2 x
师生活动：
3 分式
m m mn , , 的最简公分母是---2 3 m n n m 2 m n
3x 4 与 2 5y 2y
3ac （4）通分：：分式的通分步骤: （1）求最简公分母（2）将所有分式的分母变为最简公分母. （3）分子扩大相应的倍数。 3、我的疑问
嫩江县第二中学数学学科学案
使用时间 3.4—3.8 周序号 3 课型新授课设计人姚静哲教研组长签字
师生活动：
包组领导签字
年级八年
学生姓名
课题：16.1.分式的基本性质（3）------通分学习目标：1、理解分式通分的概念； 2、会利用分式的基本性质进行分式的通分。学习重点：分式的通分。学习难点：分式的分母是多项式的通分。使用说明与学法指导：本学案使用一课时，学习时与分数的通分进行类比。一、导入、解读学习目标： 1.分式的基本性质：一个分式的分子与分母同乘（或除以）一个 2.分数的通分： 7 与 1 12 8 二、预习案（自主学习） 1、预习内容: 教材 7 页思考之后的内容，解决两个问题：（1）什么叫做分式的通分？（2）怎样确定最简公分母？ 2 a -1 2、自我检测: （2） 3a 9 与 a 2 9 a 1 1 1 分式 , 2 , 的最简公分母是---2b 3b 4ab x y xy , 的最简公分母是--- 2 分式 2( x y ) x y 2 ，分式的值___________。三、探究案： 1、检测预习效果 2、合作、探究与展示：

分式的基本性质导学案

16、1、2分式的基本性质（3）——（通分）学习目标：1、了解分式通分的步骤和依据。

2、掌握分式通分的方法。

3、通过思考、探讨等活动，发展学生实践能力和合作意识。

重点：分式的通分。

难点：准确找出不同分母的分式的最简公分母。

一.知识准备1、把下列多项式分解因式：(1) x x 22-= ； (2) 42-a =；(3) 442+-x x = ； (4) 222ay axy ax +-=。

2、计算，并回顾如何进行计算？（1）31-21 （2）152103+ 3、利用上题尝试进行计算：（1）b a 1-1 （2）ab a 232+ 二、自主探究：1、填空：（1）()ab a 623=，()abb a 63= （2）())(1y x x x -=， ())(3y x x y x -=- 2、分式ba x abc a 22,,b 的最简公分母是; 22,y x y y x x --的最简公分母是. 3、通分（1） b a 223与cab b a 2-（2）52-x x 与53+x x解：（1）最简公分母是. （2）最简公分母是.归纳：找最简公分母的方法：通分的关键是准确找出各分式的4、巩固练习通分：(1)243bd 2c b ac 与； (2) 222)(2y x x y x xy -+与（3） a b -1与22ba a - （4）22y x x -，y x -2，y x +3；5、小结：三、课堂检测：1、通分：（1）bc a y ab x229,6 （2）16,12122-++-a a a a（3）x x xx 32,1,1+（4）a a a --11,1（5）2,422+-x x x （6）bc a bab a 215,32-（提高题）2、分式121,11,121222++-+-a a a a a 的最简公分母是（）Ａ.22)1(-a Ｂ.)1)(1(22+-a a Ｃ.)1(2+a Ｄ.4)1(-a。

分式导学案

分式导学案韶关市一中实验学校校本教材◆导学案年级：八年级学科：数学课题：16.1.1从分数到分式课型：新授课主备人：郑智化审核人：张邦国班级：姓名：使用时间：一、课前复习什么是整式？什么是单项式？什么是多项式？二、学习目标展示1、了解分式的概念.2、理解分式有意义的条件，分式的值为零的条件；能熟练地求出分式有意义的条件，分式的值为零的条件. 三、目标导学及释标根据下面的导学内容，自学课本P 2-4 （一）、分式的概念： 1、完成课本P 2[思考] 2、以上的式子v +20100，v-2060，a s ，s v ，有什么共同点？它们与分数有什么相同点和不同点？<归纳>：一般地，如果A ，B 表示两个，并且B 中含有，那么式子B A叫做分式。

3、完成课本P4练习2 ，填在下面。

(补充：πx)分式：整式：区别：（二）、理解分式有意义的条件1、问题：分式有意义，分式中的分母应满足什么条件？2、仿照课本P3例1的解题步骤完成课本P4练习3（1）（3）（5），写在下面。

（三）、（补充）分式的值为零的条件 1、当m 为何值时，分式的值为0？（1）（2） (3)1-m m 32+-m m 112+-m m_______________________ 六、作业：课本4P 练习第3题（2）（4）（6）韶关市一中实验学校校本教材◆导学案年级：八年级学科：数学课题：16.1.2分式的约分课型：新授课主备人：郑智化审核人：张邦国班级：姓名：使用时间：一、课前小测1、下列各式a π，11x +，15x+y ，22a b a b --，-3x 2，0•中，是分式的有___________；是整式的有___________；2、分式24x x -，当x_______时，分式有意义；当x_______时，分式的值为零 3、使分式||1x x -无意义，x 的值是（） A 、0 B 、1 C 、-1 D 、±1 4、下列分式，当x 取何值时有意义．（1）2132x x ++；（2）2323x x +- 二、学习目标展示1、理解分式的基本性质.2、会用分式的基本性质将分式约分. 三、目标导学及释标根据下面的导学内容，自学课本P 4-6（一）、理解分式的基本性质：1、请同学们思考：41与123相等吗？244与61相等吗？为什么？2、说出41与123之间变形的过程，244与61之间变形的过程，并说出变形依据？3、分数的基本性质是：思考：类比分数的基本性质，你能想出分式有什么性质吗？【归纳】：分式的基本性质：分式的分子与分母同乘以（或除以）一个的整式，分式的值不变。

16.1.2分式的基本性质---通分课件

1.通分的定义
2.最简公分母的定义 3.找最简公分母的方法：
1.(多项式)因式分解； 2.各分母系数的最小公倍数。 3.各分母所含相同字母（或因式）的最高次幂。 4.各分母所含有其他的字母（或因式）。
2
最简公分母：
12
a b
1、各分母系数的最小公倍数。 2、各分母所含相同字母（或因式）的最高次幂。 3、各分母所含有其他的字母（或因式）。 4、所得的系数与各字母（或因式）的最高次幂的积（其中系数都取正数）注：最简公分母与公因式的区别？
1.通分：
2c 3ac (1) 与 2 bd 4b
x 2 xy (2) 与 2 2 2 x y x y
1.将下列分数通分：
2 4 (1) 、 3 5 2 × 10 5 = 3 × 15 5 4 × 12 3 = 5 × 15 3
5 7 (2) 、 6 8 5 × 20 4 = 6 × 24 4 7× 3 21 = 8× 3 24
你能说出分数通分的数学原理吗？
填空：
a + b 3a + 3ab
2
4ab
=
12a b
2
,
2a - b 4ab - 2b 2 = 2 , 6a 12a b
2
1.你运用什么数学原理进行分式变形？
分式变形后，各分母有什么变化？
a + b 3a + 3ab = 2 4ab 12a b
2
2a - b 4ab - 2b 2 = 2 6a 12a b
2
这样的分式变形叫什么？
通分的定义：
利用分式的基本性质，把不同分母的分式化为相同分母的分式，这样的分式变形叫分式的通分。
（三）例题分析

人教版数学八年级上册15.1.2分式的基本性质(3)通分教学设计

五、作业布置
为了巩固本节课所学的通分知识，提高学生的实际应用能力，特布置以下作业：
1.基础巩固题：完成课本15.1.2节后的练习题1、2、3，重点考查学生对通分概念的理解和基本方法的掌握。
2.提高拓展题：完成课本15.1.2节后的练习题4、5，这两题涉及最简公分母的寻找和分式的加减运算，旨在提高学生的解题技巧和思维能力。
（二）讲授新知
1.通分概念：讲解通分的定义，即把几个异分母的分式化为与原来分式相等且分母相同的分式。
2.通分方法：介绍通分的方法，包括分解因式法、提公因数法等，重点讲解寻找最简公分母的方法。
3.步骤演示：通过具体例题，演示通分的过程，强调每一步的注意事项。
4.性质总结：引导学生总结通分的性质，如通分后分式的值不变等。
1.创设情境导入：
-通过生活中的实际例子，如购物时不同单价商品的比较，引出通分的概念，让学生感受到通分在现实生活中的应用。
-利用多媒体展示分式ቤተ መጻሕፍቲ ባይዱ分的动态过程，帮助学生形象理解通分的含义。
2.知识探究：
-采用问题驱动的教学方法，引导学生思考如何将不同分母的分式化为相同分母的分式。
-通过小组合作，让学生自主探究寻找最简公分母的方法，并在小组内分享经验。
四、教学内容与过程
（一）导入新课
1.生活实例引入：以购物时比较不同单价商品的数量为例，提出问题：“如何将不同单价的商品数量进行比较？”引导学生思考，激发学习兴趣。
2.回顾相关知识：带领学生回顾分式的基本性质，特别是分式的加减运算，为学习通分打下基础。
3.提出问题：引导学生思考，在进行分式加减运算时，为什么需要将分母统一？如何统一分母？
5.设计不同难度的练习题，使学生在解决问题的过程中，逐步提高自己的数学思维能力。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

16.1.2分式的基本性质---通分
学习目标：1、经历用类比、观察、联想的方法探索分式通分的方法的过程，理
解通分与最简公分母的意义.
2、能正确熟练地运用分式的基本性质将分式通分.
学习重点：确定最简公分母.
学习难点：分母是多项式的分式的通分.
学习过程：
一、自学探究
1、回顾：将异分母分数854123，，化成同分母分数为._____8
5____,41___,23=== 2、分数的通分是：把分母的分数化成分母的分数叫做分数的通分。