cl13第十三章压杆稳定

第13章压杆稳定§13.2 两端铰支细长压杆的临界压力1 2 3 两端铰支细长压杆的临界压力推导讨论分析矩形截面的细长压杆的失稳1. 两端铰支细长压杆的临界压力推导如图：两端铰支杆受压力F 作用x 处截面的弯矩M =∑研究微弯平衡状态22d d w M x EI =M Fw=−Fw EI−=22d d w F w x EI=−即 2F k EI=记已知: M Fw =−1. 推导两端铰支细长压杆的临界压力sin 0A kl= (0,1,2,)kl n n π= n k lπ=(2) x = l 时，w = 02F k EI =2()n l π=得 222n EIF lπ=若， 则 故A 不能为零，必有 0A =0w ≡sin 0kl =取 压力为最小。

22cr EIF lπ=——欧拉公式两端铰支压杆的临界压力:1. 推导两端铰支细长压杆的临界压力0,sin B w A kx==2. 讨论分析22cr EIF lπ=两端铰支压杆的临界压力 sin w A x lπ= 只适用于线弹性下两端铰支的理想压杆。

A 数值不能确定。

I -各个方向约束情况相同时，应该取最小的形心主惯性矩。

1） 2）弯曲曲线公式 ，半个正弦波曲线。

3）几点说明：举例：矩形截面在哪个平面内失稳？（绕哪个轴转动）3y h 121bI =3z bh121=I bh yI I Z ∴所以矩形截面压杆首先在xz 平面内失稳弯曲（即绕y 轴转动）.3 . 矩形截面的细长压杆失稳。

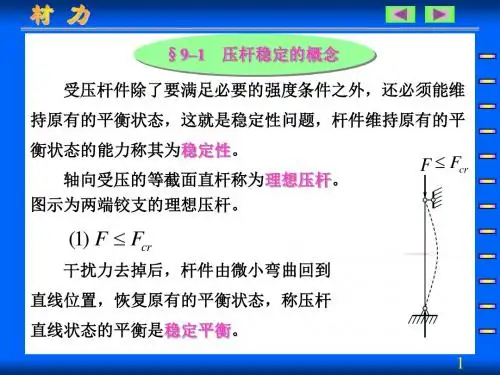
第十三章 压杆稳定§13.1 压杆稳定的概念构件受外力作用而处于平衡状态时，它的平衡可能是稳定的，也可能是不稳定的。

一、压杆稳定直杆在压力作用下，保持原直线状态的性质。

二、失稳（屈曲）压杆丧失其直线形状的平衡而过渡为曲线平衡。

三、临界压力压杆保持其直线状态的最小压力，cr F 。

§13.2 两端铰支细长压杆的临界压力在压杆稳定性问题中，若杆内的应力不超过材料的比例极限，称为线弹性稳定问题。

图示坐标系中，距原点为x 的任一截面的挠度为y ， 则该截面得弯矩为：y F M(x)cr =代入挠曲线近似微分方程，即EIM(x)-y d 22=dx 得： EIF k k dx cr y ,0y y d 2222==+ 方程通解为：0cos Asin y =+=kx B kx 由杆端的边界条件：0y 0===时，和l x x求得 ： 0A s i n ,0==kxB 解得：),2,1,0(⋅⋅⋅⋅==n ln k π222F l EIn cr π= 除n=0外，无论n 取何值，都有对应的cr F ，1n =压杆失稳时的最小荷载是临界载荷22F lEI cr π=上式称为两端铰支细长压杆的临界荷载的欧拉公式。

杆越细长，其临界载荷越小，即杆越容易失稳。

对两端铰支细长压杆，欧拉公式中的惯性矩I 应是横截面最小的惯性矩，即形心主惯性矩中的做小值min I§13.3其他支座条件下细长压杆的临界压力几种常见约束方式的细长压杆的长度因数与临界载荷例题：两端铰支压杆如图11-8所示，杆的直径20mm d =，长度800mm l =，材料为Q235钢，200GPa E =，200MPa p σ=。

求压杆的临界载荷cr F 。

解：根据欧拉公式2394122220010201024.2kN ()64(10.8)cr EI F l ππμ-⨯⨯⨯⨯===⨯⨯此时横截面上的正应力3cr P 26424.21077MPa 2010F A σσπ-⨯⨯===≤⨯⨯ 图 11-8上式表明压杆处于弹性范围，所以用欧拉公式计算无误。

第十三章 压杆稳定1 基本概念及知识要点1.1基本概念理想受压直杆、理想受压直杆稳定性 、屈曲、 临界压力。

1.2 临界压力细长压杆（大柔度杆）用欧拉公式计算临界压力（或应力）；中柔度杆用经验公式计算临界压力（或应力）；小柔度杆发生强度破坏。

1.3 稳定计算为了保证受压构件不发生稳定失效，需要建立如下稳定条件，进行稳定计算：st crn FF n ≥=－稳定条件2 重点与难点及解析方法2.1临界压力临界压力与压杆的材料、截面尺寸、约束、长度有关，即和压杆的柔度有关。

因此，计算临界压力之前应首先确定构件的柔度，由柔度值确定是用欧拉公式、经验公式还是强度公式计算临界压力。

2.2稳定计算压杆的稳定计算是材料力学中的重要内容，是本课程学习的重点。

利用稳定条件可进行稳定校核，设计压杆截面尺寸，确定许用外载荷。

稳定计算要求掌握安全系数法。

解析方法：稳定计算一般涉及两方面计算，即压杆临界压力计算和工作压力计算。

临界压力根据柔度由相应的公式计算，工作压力根据压杆受力分析，应用平衡方程获得。

3典型问题解析3.1 临界压力mm .hA I i min 551132===mm.aA I i 31632===例题13.1材料、受力和约束相同，截面形式不同的四压杆如图图13－1所示，面积均为3.2×103mm 2，截面尺寸分别为(1)、b=40mm 、(2)、a=56.5mm 、(3)、d=63.8mm 、(4)、D=89.3mm,d=62.5mm 。

若已知材料的E =200GPa ，σs =235MPa ，σcr =304－1.12λ，λp =100，λs =61.4，试计算各杆的临界荷载。

[解]压杆的临界压力，取决于压杆的柔度。

应根据各压杆的柔度，由相应的公式计算压杆的临界压力。

(1)、两端固定的矩形截面压杆，当b=40mm 时λ＞ λP 此压杆为大柔度杆，用欧拉公式计算其临界应力(2)、两端固定的正方形截面压杆，当a=56.5mm 时所以9.1291055.1135.031=⨯⨯==-i l μλkN 3752121=⋅=⋅=A EAF cr crλπσ922==ilμλ0.7d 图13－1kN63510321094121304363=⨯⨯⨯⨯-=⋅=-.).(A F cr cr σmm.d D A I i 2274122=+==kN6441023109200362=⨯⨯⨯=⋅=-..A F cr cr σλs <λ<λP 此压杆为中柔度杆，用经验公式计算其临界应力σcr2=304-1.12λ2=304-1.12×92=200.9MPa(3)、两端固定的实心圆形截面压杆，当d =63.8mm 时λs <λ<λP 此压杆为中柔度杆，用经验公式计算其临界应力(4)、两端固定的空心圆形截面压杆，当D =89.3mm ，d =62.5mm 时λ<λs 此压杆为短粗杆，压杆首先发生强度破坏，其临界应力解题指导：1．计算压杆的临界压力时，需要综合考虑压杆的材料、约束、长度、惯性半径，即需要首先计算压杆的柔度，根据柔度值，代入相应的公式计算压杆的临界压力。