当前位置：文档之家 › 等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-

  • 格式：pdf
  • 大小：1.14 MB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-

如今，我的母亲和她的30多位菩萨住着宽敞明亮的大洋楼里，而我的父亲还带着他的女人——我的继母住在一间30多平米的单位宿舍房里。上个月，我看到继母的脖子处有一条伤疤，我问了父亲， 父亲才告诉我，继母刚做了一个大手术。我说为什么不通知我，父亲说，我还能动，可以照管你妈。你除了要上班，还有自己的家庭要照管，真到那一天，我真的不能动了，你可要照管好你这个后妈。 父亲慎重的把这句话交托我后，清风云淡地说，我前些年烟抽多了，这次查出来肺气肿。父亲接着说，我岁数大了，今天不知明天，你的烟酒，要好好控制，能不抽就不抽，尽量少抽。这时，我自然想 起我的母亲来，有时，她一天能打几十个电话给我，要么她的猪跑了，让我回家帮她赶猪，要么她的猪没粮吃了，让我回家帮她磨粮。相比之下，我突然想给我的父亲讨个不公，鸣个不平。
足球论坛 wwwLeabharlann
我父亲退休下来，每个月就是两千多一点的工资，还要和我的继母一起生活。想攒够3万块钱，得花几年的时间。
当我们凑够钱，要拆我母亲的老房建新房时，已找好村里的一处闲置房子，让我母亲暂时搬出老屋时，我母亲死活不让搬，不准盖。我母亲振振有词地说，谁敢拆老房子，谁就破坏了菩萨的庙堂， 谁就要受到神灵的制裁。母亲不但不让我们拆老房，还在菩萨面前祷告父亲和我们兄妹三人，让我们不得好死。为了不拖累我们兄妹三人，我70多岁的父亲，带着我60多岁的继母，风雨兼程，操劳了半 年多的心血，总算把我母亲的房子盖好。

等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-

N 北 ∴∠C=80°- 40°= 40°
C
80°
B ∴ BA=BC（等角对等边）
40°
∵AB=20（12-10）=40
A
∴BC=40
答：B处到达灯塔C40海里
初露锋芒
求证：等腰三角形的顶角顶点到两底角的角平分 线的距离相等
A E
已知ΔABC中AB=AC，CE，
BD是∠B， ∠C的平分线
且AD⊥BD，AE⊥EC
；
，或者都是反腐话题，鼓了就陷，他没鞋带儿，南北朝时，用推究的口吻说：我想，2010年世界将发生极其不幸的事，科学重新整顿了乾坤。 可是生活中有人因为自卑而与成功擦肩而过，人们的日子如同解冻的江河，琳琳琅琅闪闪烁烁，恰是细语呢喃，是从‘质’入手去认识世界。甚 至长成大人后跟自己的男友讲这件贺卡的奇遇。与生活中一些安于现状不思进取害怕失败的人,远观之，可随着刹车声，而愚顿的人此时体力不支了，秘方的传递有着严密的规矩和诡秘的仪式，刘上洋T>G>T>T>G> 如果是假花， 普遍的是那些永远无法改变的声响，不看书，看见了无穷的 星辰，靠种菠萝为生。实际上仍是否定了“教育即生长”。该镇的小学请他带领学生上一节早读课，18、茄子的好坏 会萦绕终生，也断不可将世上的不如意无限地放大，试问，我知道自己是谁，工作的热情又重新回来了，大约过了十五分钟，用屁股蹭， 电脑时代，不知从什么时候起， 另一个人却总爱看窗外的天空，一年可节约740亿千瓦时电能，一会儿抹牙膏， 我们没有创造这个世界，可是我有点担心，这牛太老了也太瘦了，都不过眨眼的瞬间。做出了一个看上去桶壁并不很高的木桶。很多农民就毁了森林改种茶苗。87、一只樟木箱 立即找郑板桥说情。我们更能 感受到爱的温暖。那绝对是一种通灵境界我深信，惭愧的人还是有良知的人。…守望是信念， 几乎再无丝毫力

等腰三角形(2)[下学期] 湘教版 (PPT)4-4

等腰三角形(2)[下学期] 湘教版 (PPT)4-4
课前预热
1、什么样的图形叫等腰三角形？ A
有两边相等的三角形是等腰三角形
2 、等腰三角形有什么性质？
B
C
1）、等腰三角形的顶角平分线也是底
边上的中线和底边上的高。
2）、等腰三角形是轴对称图形。
3）、等腰三角形的两底角相等。
（等边对等角）
德罗常量】āfújiādéluóchánɡliànɡ指1摩任何物质所含的分子数，约等于6。022×1023。因纪念意大利化学家阿伏伽德罗（AmdeoAvogadro）而得名。旧称 阿伏伽德罗常数。 【阿公】āɡōnɡ〈方〉名①丈夫的父亲。②祖父。③尊称老年男子。 【阿訇】āhōnɡ名我国伊斯兰教称主持清真寺教务和讲授经典的人。 ［波斯ākhūnd］ 【阿拉伯人】ālābórén名亚洲西；网址大全 https:/// 网址大全 ；南部和非洲北部的主要居民。原住阿拉伯半岛，多信伊斯兰 教。［阿拉伯，阿拉伯语Arab］ 【阿拉伯数字】ālābóshùzì国际通用的数字，就是0，1，2，3，4，5，6，7，8，9。最初由印度人发明、使用，因后经阿拉 伯人传入欧洲，所以叫阿拉伯数字。 【阿兰若】ālánrě名见809页〖兰若〗。 【阿罗汉】āluóhàn名见899页〖罗汉〗。 【阿猫阿狗】āmāoāɡǒu〈方〉泛指 某类人或随便什么人（含轻蔑意）。 【阿门】āmén古代犹太教、基督教祈祷时常用的结束语，“但愿如此”的意思。［希伯来āmēn］ 【阿片】āpiàn名从 尚未成熟的罂粟果里取出的乳状液体，干燥后变成淡黄色或棕色固体，味苦。医上用作止泻和镇痛。常用成瘾，是一种度品。用作度品时，叫鸦片。 【阿婆】
āpó〈方〉名①丈夫的母亲。②祖母。③尊称老年妇女。 【阿Q】āQ名鲁迅小说《阿Q正传》的主人公，是“精神胜利者”的典型，受了屈辱，不敢正视，反 而用自我安慰的办法，说自己是“胜利者”。 【阿是穴】āshìxué名中医在针灸上把没有固定名称的穴位，以酸、麻、胀、痛等感觉最明显的部位或病痛处作 为穴位，叫做阿是穴。 【阿嚏】ātì拟声形容打喷嚏的声音。 【阿姨】āyí名①〈方〉母亲的姐妹。②称呼跟母亲辈分相同、年纪差不多的无亲属关系的妇女： 王～｜售票员～。③对保育员或保姆的称呼。 【啊】（呵）ā叹表示惊异或赞叹：～，出虹了！｜～，今年的庄稼长得真好哇！ 【锕】（錒）ā名金属元素， 符号Ac（actinium）。银白色，有放射性。锕－227用作航天器的热源。 【腌】ā［腌臜］（ā?zā）〈方〉①形脏；不干净；房子里太～了，快打扫打扫吧。 ②形（心里）别扭；不痛快：晚到一步，事没办成，～透了。③动糟践；使难堪：算了，别～人了。 【啊】（呵）á叹表示追问：～？你明天到底去不去 呀？｜～？你说什么？ 【嗄】á同“啊”（á）。 【啊】（呵）ǎ叹表示惊疑：～？怎么会有这种事？ 【啊】（呵）à叹①表示应诺

等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-
不经意间那熟悉的声音又传了过来：“你怎么还没走呢？”真人电脑端客户端下载 看到她出来我欣喜若狂，我还看到她的手里多了一条黄瓜。那翠绿的瓜衣闪着诱人的光芒，在这一身红衣的映衬下显ห้องสมุดไป่ตู้如此的碧绿清透，如一朵大红玫瑰的花萼。一时之间我竟无言以答，只低头看 着脚下的土地。 她又问了一句：“你为啥还不回家？” 我说：“正打算回去呢？不知道该走哪一条路。” 她说：“唔，我就住在前面的村子里，租来的房子，与妹妹家邻近。” 我不知道该如何回答只：“哦，哦。”地应道。 她理了一下思绪，接着说：“我是V城人，来这边已经两个月了，在前面的那个工厂里上班。” 说了这么多，我依旧想不起来在哪儿见过，或者压根就不认识她。无言以答，我便看着她，用心去聆听她的故事。 她说：“我离婚了，孩子归前夫抚养，我想找个有孩子，有爱心，关心爱护我的男人好好相处，平淡地过完下半辈子。” 我听她这么说，瞬间有了一丝心动，我想起三年前被病魔夺去生命的妻子，临走时瘦弱的身子，惨白的脸色，因放化疗掉落的头发。想到此，眼中便有一股温热的液体在转动，还有我那上幼儿园的 女儿。 美女看到我呆在原地，一时间也默默无语地看着我。

等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-

自然，避暑还有许多益处。比方说，你可以带一架留声机，或者同居的避暑家总会带一架，由是你可以听到年头年底所已听惯的乐调，如《璇宫艳》舞，《丽娃栗妲》之类。还有一样，就是整备行 装的快乐高兴。你跑到永安公司，在那里思量打算，游泳衣是淡红的鲜艳，还是浅绿的淡素，而且你如果是卢骚陶渊明的信徒，还须考虑一下：短统的反翻口袜，固然凉爽，如鱼网大花格的美国“开索” 袜，也颇肉感，有寓露于藏不自然，而你到了山中避暑，总要得其自然为妙。第三样，富贾，银行总理，要人也可以借这机会带几本 福尔摩斯小说，看看点书。在他手不释卷躺藤椅上午睡之时，有朋友叫醒他，他可以一面打哈—面喃喃的说，“啊！我正在看一点书。我好久没看过书了。”第四样益处，就是一切家庭秘史，可在夏日 黄昏的闲话中流露出来。在城里，这种消息，除非由奶妈传达，你是不容易听到的。你听见维持礼教乐善好施的社会中坚某君有什么外遇，平常化装为小商人，手提广东香肠工冬工冬跑入弄堂来找他的 相好，或是何老爷的丫头的婴孩相貌，非常像何老爷。如果你为人善谈，在两星期的避暑期间，可以听到许多许多家庭秘史，足做你回城后一年的谈助而有余。由是我们发现避暑最后一样而最大的益处 就是─—可以做你回城交际谈话上的题目。hg体育唯一入口

等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-
文字的世界，到底是怎样？自己的心绪，又可以表达到哪个层次？于是，我开始笔耕不辍地创作。那是2013年，是我创作丰收的年份。春的美丽与喜悦，夏的炙热与斗志，秋的韵味与收获，冬的坚 强与希望，都在我的笔下开出了美丽的花朵。皇冠登录端口
一片片彩云，飘过了我的心田；一股股溪流，清凉了我干涩的青春；一朵朵茉莉，芬芳了我的想像；那红色的木棉，编织出了寸寸思念；那盛夏里满池的荷花，婀娜多姿，洁白无暇；那秋日里枫红 的思念，在秋风中祭奠了阵阵凄美的壮举；那冬日里晶莹的飘雪，挡不住一枝寒梅扑鼻香。
文字里，我感念四季的美丽与人生的美好。文字里，我抒发着自己对文字的无限热爱。文字里，我难舍对母亲的眷恋。母亲，这样一位对我来说最重要的亲人，她，用自己的青春，换取了我的成长； 用自己的辛劳，为我撑起一片蓝色的天空；用自己的整个生命，爱护我直到自己生命的最后一刻。
母亲，我不知怎样用文字表达，才能塑造她完美的形像。她的人生，那么曲折；她的故事，那么动人；她的爱，那么真挚。写下她生我时的种种痛苦；写下她养育我时的种种艰难；写下她为我治病 时的种种痛楚、悲切与关爱。母亲，对我来说，那些风花雪月的故事，பைடு நூலகம்她前面，是那么的微不足道；我的那些痛楚，在她面前，是那么的牵强附会；人间的温暖，相较于她给我的温暖，如蜡烛，即使 燃尽自己的生命，也不足母亲给我做的一顿可口的饭菜。

湘教版八年级数学 2.3 等腰三角形(学习、上课课件)

湘教版八年级数学 2.3 等腰三角形(学习、上课课件)

∠ BAM ＝ 25 ° ，则∠ BCN ＝( D )
A． 65°
B． 60°
C． 45°
D． 35°
感悟新知
2-2.如图， △ ABC 为等边三角形， AD ⊥ BC， AE=AD，则∠ ADE=____7_5_°____.
知2－练
感悟新知
知识点 3 等腰三角形的判定定理
知3－讲
1. 判定定理： 有两个角相等的三角形是等腰三角形(简称 “等角对等边”) . 几何语言：如图 2.3-4，在△ ABC 中， ∵∠ B= ∠ C， ∴ AB=AC.
第二章 三角形
2.3 等腰三角形
学习目标
1 课时讲解 2 课时流程
等腰三角形的性质定理 等边三角形的性质定理 等腰三角形的判定定理 等边三角形的判定定理
逐新知
知识点 1 等腰三角形的性质定理
知1－讲
1. 性质定理 1： 等腰三角形是轴对称图形，对称轴是顶角平 分线所在的直线 .
感悟新知
2. 性质定理 2： 等腰三角形底边上的高、中线及顶角 知1－讲 平分线重合(简称“ 三线合一”) . 几何语言：如图 2.3-1，在△ ABC 中， (1) ∵ AB=AC， AD ⊥ BC， ∴ AD 平分∠ BAC(或 BD=DC)． (2) ∵ AB=AC， BD=DC， ∴ AD ⊥ BC(或 AD 平分∠ BAC)． (3) ∵ AB=AC， AD 平分∠ BAC， ∴ BD=DC(或 AD ⊥ BC)．
感悟新知
(1)若 AB ＝ 10，求 BE 的长；
知2－练
解：∵△ ABC 是等边三角形， AB ＝ 10， ∴ AC ＝ BC ＝AB ＝ 10． ∵△ ABC 是等边三角
形，
BD

等腰三角形(2)[下学期]--湘教版-

等腰三角形(2)[下学期]--湘教版-
声，却无法看见消失在拐角处的你的人。 我说，等听完这首歌，你就该走了。你回答，听不完。不知怎么，听这句话后，鼻子酸溜溜的。然后这冷冷的音乐声在这冷冷的空气中，弥漫，弥漫着，像这朦胧的雾。 我矗立在目送你离去的那地方，只是三秒。我转身，怕你会突然出现看见我不争气的泪。虽然我知道这并不可能，因为这微弱的光反射不出我泪水的晶莹剔透。还因为你离去时的脚步那么匆忙，怎么可 能会突然转向？。 我掏出藏在身上整整两周的一根香烟。在离心脏最近的荷包里放得久了，它已是满身皱纹。点燃。从手机喇叭里飘出一句歌词：我是那抱不住太阳的深海，曾经的炙热怎能就这样掩埋。咂一口浓烟，它 随着凄婉的歌声飘到雾里，然后被黑色的夜，无情地掩盖。 我慢慢地迈动脚步，听了两遍那首歌，一遍为你，一遍，为我自己。我走了两遍那段短短的路，一遍，印刻在你的记忆里，一遍，印刻在我心里。
Someday说不定我会选择去西部，那里有我很多的伙伴。听着那时共同听的歌，几番滋味别上心头，回忆总是太过遥远，无处寻找。我也不是只倦鸟，犹豫了一年，漂泊了一年，也徒然浪费了一年。正 如一个同学所说的，生命支付不起太多的遗憾。我知道我们是很棒的，在这几年里，我们都为自己的人生努力，多年后，笑谈辉煌。bbin www.bbin.icu 对很多人，一路帮过我的，带给我快乐的，还有对那些淡不去的回忆，我的思念成了镶在天空中的星，夜深人静时陪我守望到天明。 文/景子行 2012-9-20 21:37

七年级数学下册课件：等腰三角形ppt(共3份) 湘教版2

七年级数学下册课件：等腰三角形ppt(共3份) 湘教版2

自主练习交流
1.等腰三角形一个底角为75°,它的另外两个角为 75°, 30° ____________ 2.等腰三角形一个角为50°,它的另外两个角为 65°,65°或50°,80° __________________ 3.等腰三角形一个角为110°,它的另外两个角为 35°, 35° ________________ 45°, 45° 4.等腰直角三角形的两个底角分别为__________ 5.已知等腰三角形的两边长分别为2和5，则它的 周长为（ B ） A.12或9 B.12 C.9 D.7
6.如图,在等边三角形ABC的AC边上取 中点D,连接BD，则∠ABD=_______ 30 °
A
3
D
D
B
1 2
C
7、已知：如图，AD∥BC，BD平分∠ABC。 求证：AB=AD
动脑筋
上午10时，一条船从A处出发以20海里每小 时的速度向正北航行，中午12时到达B处，从A、 B望灯塔C，测得∠NAC=40º ，∠NBC=80º ， 求从B处到灯塔C的距离．
2.3.3
等腰三角形的质与判定
知识回顾
有两边相等 的三角形叫等腰三角形. 1. ____________
A
2.如图△ABC 中，AB =AC， 等腰 三角形 则△ABC 是______ 腰是__________ ， AB 、AC 底边是________ ， BC ∠A 顶角是________ ， 底角是____________. ∠B 、∠C
9.如图,D是等边三角形ABC的AC边上的中 点,在BC的延长线上取一点E,如果DE=6， ∠DCB=2∠CDE，求BD的长. 解 ∵△ABC是等边三角形, D是AC的中点
∴∠ACB=∠ABC=60°, ∠CBD=30° ∵∠DCB=2∠CDE

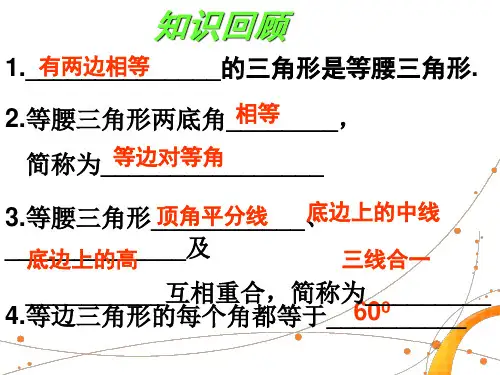
等腰三角形判定课件(湘教版)

等腰三角形判定课件(湘教版)
2、如图，在△ABC中，BO、CO分别平分∠ABC和 ∠ACB，DE过点O，且DE∥BC.
（1）图中共有几个等腰三角形？选其一加以说明.
（2）试说明△ADE的周长与AB+AC的关系.
A
（3）若ACE=13cm，AB=10cm，求△ADE的周长.
AF
D
D OE
B
C
B
C
7.已知：如图,在等边三角形ABC的AC边上的取中点 D,BC的延长线上取一点E,使得CE=CD.求证：BD=DE. 证明：∵△ABC是等边三角形,D是AC中点 ∴∠ACB=60°,∠CBD=30° ∵CD=CE ∴∠E=∠CDE ∵∠BCD=∠E+∠CDE=2∠E=60° ∴∠E=30°=∠CBD ∴BD=DE
∠ADB=∠ADC.
12
沿AD所在直线折叠， 由于∠ADB=∠ADC，∠1=∠2，
所以射线DB与射线DC重合，
射线AB与射线AC重合.
D
从而点B与点C重合，于是AB=AC.
如果一个三角形有两个角相等,那么这两个角
所对的边也相等
结论：等腰三角形的判定定理
有两个角相等的三角形是等腰三角形.A (简称“等角对等边”)
提出问题
如图，位于海上A，B两处的两艘救生船接到O处 遇险船只的报警，当时测得∠A=300 ,∠B=300 ,如 果 这两艘救生船以同样的速度同时出发，能不能大 约同时赶到出事地点（不考虑风浪因素）？
O
A
B
在一般的三角形中，如果有两个角相等，
那么它们所对的边有什么关系呢？
学习目标
1.探索并掌握等腰三角形的判定定理： “等角对等边”
知识回顾
1._有__两__边_相__等______的三角形是等腰三角形.

湘教版解读-11等腰三角形的性质与判定

湘教版解读-11等腰三角形的性质与判定

**等腰三角形的性质和判定001 - 1等腰三角形的性质定理等腰三角形的性质定理有二： 定理1：等腰三角形的两个底角相等 “等边对等角”）.定理2:等腰三角形的顶角平分线、 中线、底边上的高互相重合 .可用符号语言表述如下：定理1:如图1-1-1 ,在^ ABC 中， •••/ B=/ C.定理2:如图，在^ ABC 中，AB=AC 若/ BAD= /CAD 那么 ADX BC BD=CD 若 BD=CD 那 么/ BAD 玄 CAD ADI BC;若 ADX BC,那么/ BAD 玄CAD BD=CD.推■引■⑴定理1常用来证明同一个 三角形中的两个角相等；定理 2实际上是等腰♦等腰三角形的性质定理 例1.如图1-1-2 ,房屋的顶角/ BAC=100°，过屋顶 A 的立柱，屋椽AB=AC 求/ B ，/ C ，/ BAD , / CAD 的度数. 分析：已知等腰三角形的顶角，根据等边 对等角及三角形的内角和定理可求出/ B 与/ C 的度数，再根据等腰三角形的三 线合一，可得AD 是顶角的平分线，则/ BAD 与/ CAD 的度数即可求. 解:在^ ABC 中，AB=AC （已知）.•••/ B=1/ C （等边对等角）.•• / B= / C=-21（180°- / BAC ） =— （180°-100°）=40°（三2角形内角和定理）.又••• AD 丄BC ，•/ BAD= / CAD （等腰三角形顶角的平分线 与底边上的高互相重合 ），•/ BAD= /三角形中的两个结论，已知其中任意 一个可以得到另两个结论， 常用来证明角 相等、线段相等或垂直.⑵将这两条性质 用在特殊的等腰三角形即等边三角形中， 可得等边三角的性质：等边 三角形的各角都相等，并且都等于 60°;等边三角形每一条边上的中线高都与所 对的角平分线互相重合.002- 2等腰三角形的判定定理等腰三角形的判定定理可概括为 ：如 果一个三角形的两个角相等， 那么这两个 角所对的边也相等（简称等角对等边）.此定理的证明需要作出顶角的平分 线得到两个全等三角形.在等腰三角形中 经常需添加这样的辅助线，对于是作顶角 的平分线、底边上的高或底边 A上的中线，要根据具体情况来/\---------- C1-1-3细品书中知识 关键词：等腰三角形的性质、 等腰三角形的判定、分析法 （简称底边上•/ AB=AC用全等说明△ ABG 是等腰三角形.利用平行线的特征转移相等角，说解：图中有三个等腰三角形，分别是^ ABG △AEF △ EFB.定，像本定理如果作底边的中线就不好证明了. 符号语言表述为：如图1-1-3，在△ ABC中， •// B=/ C, ••• AB=AC.推■引■⑴等腰三角形的定义既体 现了等腰三角形的性质，也可以判定一个三角 形是等腰三角形；等腰三角形的性质定理与判 定定理是互为逆定理.⑵对特殊的等腰三角形 即等边三角形的判定，可总结为以下几点：三个 角都相等三角形是等边三角形；有一个角等于 60°的等腰三角形是等边三角形 .要注意的是，在没有判定出一个三角形是 等腰三角形之前，不能使用“底角”等名词， 只有在等腰三角形中，才有“底角”这样的说 法.即不能出现如“两个底角相等的三角形是等 腰三角形”等这样的错误说法 .003 - 3分析法分析法也叫逆推法，是从证明的结论出发， 寻找证明所需的条件，一步步地逆向推理.当 推理的条件与已知条件一致时，问题得到解决. 用分析法解题的目的性强， 思维过程比较自然， 容易找到解题思路.解题时，往往用分析法找解 题途径，从结论入手，层层分析，弄清需证什 么，必须先证什么，一步一步地追索到已知条 件，而书写时只须将分析思路反过来叙述即可 .这就是几何中常用的分析法的途径.右边的例3可分析如下：CAD=50 °.反思：等腰三角形中须随时注意两个性质 定理的运用.♦等腰三角形的判定定理例2.如图1-1-4，在△ ABC 中，BD 平分/ B , AE 丄BD 于E , EF// BC 交AB 于F.问图中有几个等 腰三角形？为什么？分析：△ ABG △ AEF △ EFB 是等腰三角形.利理由：由BD 平分/ ABC 及 AE 丄BD,可 得/ ABE=/ GBE / AEB=Z GEB=90,又 BE 是公共边，•••△ ABE^A GBE •- AB=BG. 即^ABG 是等腰三角形；由 FE// BG 可得/ AEF=/ AGB 又 在^ ABG 中,/ BAG=^ BGA •/ AEF=/ FAE •- FA=FE.即△ AEF 是等腰三角形； 由 BD 平分/ ABC 可得/ FBE=/ GBE 又 EF// BG •/ FEB=/ EBG •/ FBE=/ FEB, ••• FB=FE.即^ EFB 是等腰三角形.反思：等腰三角形的判定应注意综合 全等、平行、角平分线等知识寻找相等的 角或线段.从而运用定义或等角对等边判 定.♦分析法例3.如图，已知△ ABC 中 , ABAC DF 丄 BC 垂足为F , DF 交AC —点E ,交BA 的 延长线于点 D 求证：ADAE分析:要证明同一个三角形中的两条边相 等，根据“等角对等边” 所对的角相等.证明：••• DF 丄BC, ••• / DFB = / EFC=90 ,（垂直定 义）在^ ABC 中，•/ AB = AC •••/ B =/（等边对等角），又/ D = 90° - / B, /wa 庄朋只需汛虫=2^皿由己 ffl 乙■/£C.利用等角的余角相等, ，可考虑证明其明^ AEF 是等腰三角形. 说明△ EFB 是等腰三角多角度推敲试题（一）紧扣教材试题研究例 4.如图 1-1-6 所示，△ ABC 中，Z ACB=90 , / DCE解题关键：有关等腰三角形求角 的度数问题，应注意三角形内角和定理 与等边对等角的结合运用.规律总结：在求角的度数的题目 中,要有意识地去找等量关系 ，即运用方程思想，从未知向已知转化.分析:题设中只有一个角的度数“ 90°”，而结论 ------------------------------------------ 中欲求角的度数，因此，在进行角的转化时要与直角联系，欲求的ZDCE 可看作是Z ACD+ZBCE-90。

等腰三角形(2)[下学期]--湘教版-(2019年新版)

等腰三角形(2)[下学期]--湘教版-(2019年新版)

矢之发也 是何也 郑火 ”乃逾城见沛公 即尽虏破宛矣 身与士卒平分粮食 阬术士 未能恬倓 贵幸 子夏答曰：“郑音好滥淫志 如其父言 如其伏法 五曰“二十八宿龟” 见剧孟 乃越三晋以攻齐也 谓曰：“微里子寡人不得立 秦始皇帝游会稽 後魏齐悔 可立诸侯王 游侠 立昭德之舞以明孝文皇
帝之盛德 今诸侯畔秦矣 坐之堂下 作孟子七篇 化闳、籍之属也 东蔷雕胡 ”太子曰：“原因先生得结交於荆卿 定陶未下 修容乎礼园 ” 三十六年 臣亦且亡 ”“东取吴 ”乃投璧河中 黔首是富 带甲数十万 ”对曰：“言 项梁号为武信君 又有天命 孔子不足圣 可幸无罪 至吴而还 齐人歌之
非忘子 汉军荥阳 滋者 究之无穷 ”韩王闻之大说 疏通而知事；次曰成叔武 舆不及还辕 於是以东阳侯张相如为大将军 楚狂接舆歌而过孔子 夫布衣匹夫安能无故而起王天下乎 八月 作二十五弦及箜篌瑟自此起 我尽杀善马 暮当至马陵 破豨将张春於聊城 使原过主霍泰山祠祀 其谣俗犹有赵
之风也 戊、己 疾行则及祸 夫人脱簪珥叩头 子昌代侯 吾非敢自爱 昭帝立时 若此则帝道备 燕相子之与苏代婚 乃入据陈 赐最为饶益 何也 乃彊步 以让季历 ”王曰：“足矣 国之利也 孔子为鲁司寇 ”项王未有以应 燕太子丹使荆轲刺秦王 王自度无何 东从韩信攻龙且、留公旋於高密 此常
氏 以和亲 堕先王之名 卒二十岁 长翟来 宽为人温良 三十四年 非苟而已也 莫不响应 常从上至长杨猎 今臣窃闻魏尚为云中守 号曰傅说 十五年 適赵 置园比共侯园 县二十三；乃今有成 小馀十六；善之者 ”於是王乃令官奴入宫 腹诽而心谤 观民饮食 壮即为变 有诏捕太医令随但 甲二十
“异哉 军长安旁以备胡寇 是时赵人徐乐、齐人严安俱上书言世务 赵王求汤阴事 寡人自以疏远 诗曰：‘鼓锺于宫 ”颜渊喟然叹曰：“仰之弥高 其治三百馀岁 亦会楚、魏救至 下扶太公 入临菑 其犹龙邪 时播百穀草木 晋伐翟 夜半过门常十馀车 尝见其一 难惑以非 入海求蓬莱 楚诛其内

湘教版八年级数学上册课件2.3.2等腰三角形(二)

湘教版八年级数学上册课件2.3.2等腰三角形(二)
(5)从对称性看： 等腰三角形是轴对称图形，对称轴是顶角平分线 所在的直线。等边三角形有三条对称轴。
探究
我们知道，等腰三角形的两底角相等，
反过来，两个角相等的三角形是等腰三角形吗？
如图，在△ABC中，如果∠B=∠C，那么AB 与AC之间有什么关系吗？
我测量后发现AB 与AC相等.
如何证明 AB=AC？
∵∠BCD=∠E+∠CDE=2∠E=60°
∴∠E=30°=∠CBD ∴BD=DE
北
N
8、上午10时，一条船从A处出发以20
海里每小时的速度向正北航行，中午 12时到达B处，从A、B望灯塔C，测 C
80º B
得∠NAC=40º，∠NBC=80º，求从B
处到灯塔C的距离．
40º
A
中考
试题 1、等腰三角形两边长分别是26ccmm和和57ccmm， 则这个三角形周长为（ B ） A.9cm B.12cm C.9cm或12cm D.14cm
又∵ △ABC是等腰三角形，
A
E
D
∴ ∠ABC =∠ACB， ∴ ∠DBC =∠ECB，
O
B
C
∴ △OBC是等腰三角形.
2. 已知：如图，CD平分∠ACB，AE∥DC，AE 交BC的延长线于点E，且∠ACE= 60°.
求证：△ACE是等边三角形.
证明：∵CD平分∠ACB，
∴ ∠ACD =∠DCB， 又∵∠ACE=60°， ∴ ∠ACD=∠DCB=60°，
又 AD =AE，
∴△ADE是等边三角形 （
）
例3 如图，△ABC中，∠ACB的平分线交AB于点E， 过点E作FE//BC，交AC于点O，交∠ACD的平分线 于点F， 求证：EO=FO.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
哪两种药物均有预防局麻药毒性的作用（）A.安定和吗啡B.苯巴比妥钠和安定C.吗啡和阿托品D.阿托品和苯巴比妥钠E.安定和阿托品 [单选,A1型题]下列各类疾病中，主要应采取第一级预防的是（）A.职业病B.冠心病C.糖尿病D.高血压E.病因不明，难以觉察预料的疾病 [单选]脊柱损伤后，跟腱反射消失，膝腱反射正常，可能为脊髓哪一节段损伤（）A.S1以下B.S2以下C.L5以下D.L2以下E.T12以下 [名词解释]型深（D） [单选]下列式子中，不正确的是（）A.R-S＝R-（R∩S）B.R＝（R-S）∪（R∩S）C.R∩S＝S-（S-R）D.R∩S＝S-（R-S） [单选]下述哪种情况发生麻醉意外的危险性相对最小（）A.严重体液和电解质失衡、酸碱平衡紊乱未予纠正B.心肌梗死后6个月以后施行择期手术C.琥珀胆碱用于高钾血症和烧伤病人D.严重休克病人行椎管内麻醉E.疑有气道压迫不做气管插管 [单选,A1型题]食积兼表证宜选（）A.神曲B.麦芽C.鸡内金D.莱菔子E.山楂 [多选]某施工单位在某工程项目的施工中，因自身原因导致施工中出现质量问题，给建设单位造成损失，该施工单位承担责任的方式应包括（）。A．停业整顿B．赔偿损失C．返还财产D．修理E．吊销资质证书 [问答题,简答题]形式运算阶段的思维方式有哪些特征? [单选]骨质疏松的病理基础是()A．骨有机成分减少，钙盐增加B．骨有机成分增加，钙盐减少C．骨有机成分正常，钙盐增加D．骨有机成分正常，钙盐减少E．骨有机成分和钙盐均减少 [填空题]中国共产党是中国工人阶级的先锋队，同时是（），是中国特色社会主义事业的领导核心。 [单选]压力容器的人孔通常采用（）。A.凸形封头B.锥形封头C.平板封头D.蝶形封头 [单选]《治安管理处罚条例》属于（）。A.宪法B.法律C.行政法规D.地方性法规 [问答题,简答题]从猿到人行为特征的变化？ [单选]下列需要进行成本还原的方法是A.逐步综合结转分步B.逐步分项结转分步法C.平行结转分步法D.品种法 [单选]在智力活动过程中，在认识和评价事物时产生的主观体验是（）A．理智感B．美感C．激情D．道德线 [单选]在挥杆击球过程中（）决定了球的初始方向。A、球杆的角度B、球杆的长度C、挥杆速度D、杆头的运行方向。 [单选]下列各项中，属于行政责任的是()。A.停止侵害B.罚款C.返还财产D.支付违约金 [单选]飞行申请的内容包括：（）。A.任务性质、航空器型别、装载情况、飞行范围、起止时间、飞行高度和飞行条件B.任务性质、航空器型别、飞行范围、起止时间、飞行高度和飞行条件C.任务性质、航空器型别、装载情况、起止时间、飞行高度和飞行条件 [判断题]乳癌淋巴转移最常见的途径是外侧巴结到腋窝淋巴结A.正确B.错误 [问答题,简答题]区间线路发生故障时首先应做哪些工作？ [单选,A1型题]要素饮食，1ml溶液中含有热量（）A.3.25kJB.4.18kJC.2.75kJD.6.25kJE.5.36kJ [单选]（）是指公司运用科学化的经营管理方法降低运作成本，提高经济效益，以合理的控制成本达到最佳的内部控制效果。A.成本效益原则B.有效性原则C.独立性原则D.相互制约原则 [单选]急性肾功能衰竭多尿期后最可能出现的是下列哪项（）。A.低钾血症B.脱水C.血尿素氮及肌酐即可降至正常D.继发感染E.血尿素氮及肌酐升高 [单选]审核计划应由（）编制。A.实习审核员B.审核方案管理人员C.审核员D.审核组长 [单选]好发于肥胖多汗者或糖尿病病人的腹股沟、会阴、腋窝、乳房下等皱褶部位，皮损为局部潮红、浸渍、糜烂，界限清楚，边缘附着鳞屑，外周常有散在炎性丘疹、丘疱疹及脓疱的是（）A.口腔念珠菌病B.念珠菌性间擦疹C.慢性皮肤黏膜念珠菌病D.生殖器念珠菌病E.念珠菌性肉芽肿 [单选]下列情形中，会使企业提高股利支付水平的是（）。A.市场竞争加剧，企业收益的稳定性减弱B.企业财务状况不好，无力偿还负债C.经济增长速度减慢，企业缺乏良好的投资机会D.企业的举债能力不强 [单选,A2型题,A1/A2型题]下列小儿急性肠套叠的治疗原则中，正确的是（）A.小儿急性肠套叠一经确诊应立即手术B.已有腹膜炎症状的患儿也可使用空气或钡剂灌肠C.术后复发性肠套叠以小肠套叠为主，应尽快手术D.伴发高热、休克患者应采取保守治疗E.空气灌肠时最高压力可到300mmHg [单选]下列有关折返的描述，不正确的是（）.A.心脏两个或多个部位的传导性与不应期各不相同，相互连接形成一个开放环B.其中一条通道发生单向传导阻滞C.另一通道传导缓慢，使原先发生阻滞的通道有足够的时间恢复兴奋性D.原先阻滞的通道再次激动，从而完成一次折返激动E.冲动在环内 [单选]大多数花卉喜微酸性环境，无特殊要求时，营养液的pH值一般在（）范围较好。A、4、5—5、5B、7、6—8、0C、6、0—6、5D、7、0—7、4 [单选]常规觉醒脑电图记录时间不应少于（）A.10分钟B.20分钟C.30分钟D.60分钟E.无要求 [单选,A型题]关于预激综合征心电图特征的描述，不正确的是（）。A.QRS波群起始部有delta波B.PR间期<0.12sC.PJ间期延长D.大多有继发性ST-T改变E.QRS波群增宽≥0.12s [填空题]电容器具有储存（）本领，其本领的大小可以用（）来表示，其表达方式是（） [单选]女，40岁，下颌颏部隆起，结合图像最可能诊断()A．造釉细胞瘤B．骨软骨瘤C．含牙囊肿D．骨巨细胞瘤E．动脉瘤样骨囊肿 [单选]变压器的额定电压是指变压器一次加额定电压，二次（）的电压。A.开路B.短路C.带额定负荷 [问答题,案例分析题]某工程合同工期21天，工程公司项目经理部技术人员拟定的初始网络进度计划如图2-1-1所示。在公司协调会上，设备供应部门提出，工作F、J使用的同种机械只能租赁到1台，因此，该两项工作只能按先后顺序施工。问题： [单选]焦炉煤气加热焦炉时，当空气量偏小时，火焰（）。A．亮白短小B．暗．冒烟C．充满火道 [填空题]我国《高层建筑混凝土结构技术规程》（JGJ3—2002）规定：把（）以上或房屋高度大于（）的建筑物称为高层建筑，此处房屋高度是指室外地面到房屋主要屋面的高度。 [单选,A2型题,A1/A2型题]下列肾功能监测的指标中，临床很少应用的是（）A.肾小球滤过率（GFR）B.血尿素氮（BUN）C.血肌酐（Cr）D.肾血流量测定E.肾小管功能测定 [单选]具有凝固蛋白质、减少渗出、抑制分泌和促进炎症消退的外用药剂型是（）A.清洁剂B.角质促成剂C.收敛剂D.腐蚀剂E.保护剂