晶胞空间利用率的计算教学文案

晶体密度、空间利用率的通用计算方法以金属晶体为例进行分析，计算方法如下：第一步，确定晶胞含有的微粒数。

若1个晶胞中含有x 个微粒，则： (1)1个晶胞中原子利用的体积 = x ·4 π r 3 / 3 ，其中r 表示金属原子半径。

(2)1个晶胞质量 = x ·M / N A ，其中M 表示金属的摩尔质量，N A 表示阿伏加德罗常数。

若计算对象是离子晶体，该式亦然成立，M 则表示离子化合物的摩尔质量。

第二步，计算晶胞体积。

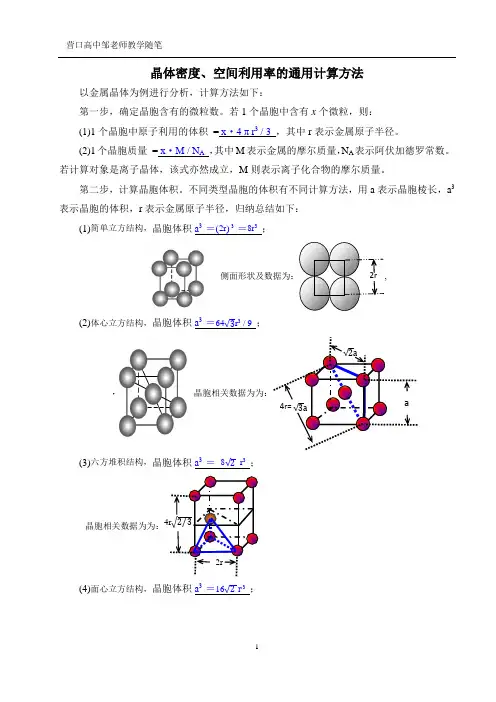
不同类型晶胞的体积有不同计算方法，用a 表示晶胞棱长，a 3表示晶胞的体积，r 表示金属原子半径，归纳总结如下：(1)简单立方结构，晶胞体积a 3 ＝(2r ) 3 ＝8r 3 ；侧面形状及数据为：,(2)体心立方结构，晶胞体积a 3 ＝64√3r 3 / 9 ；(3)六方堆积结构，晶胞体积a 3 ＝ 8√2 r 3 ；晶胞相关数据为为：(4)面心立方结构，晶胞体积a 3 ＝16√2 r 3 ；a√2a√3a4r= 2r(1)有关晶体密度的计算通用关系式：x·M /N A＝ρ·a3，依据是晶体密度等于晶胞密度，具体计算时把各类型晶胞的体积，代入关系式即可，下式亦同。

(2)有关空间利用率的计算通用关系式：x·4 πr3 / 3＝w%·a3，其中w% 表示晶胞空间利用率。

注意事项：(1)在实际计算时要注意长度单位换算，晶胞棱长及原子半径单位常用pm，而密度中的体体积单位常用(cm)3，存在换算关系1pm=10-10cm。

(2)若计算离子晶体密度，方法大同小异，需要综合考虑阴、阳离子半径来求晶胞体积。

常见金属晶胞结构与性质归纳一览表：。

常见晶体空间利用率的计算晶体空间利用率是晶格中原子或分子所占体积与晶胞体积之比。

它是描述晶体中原子或分子排列紧密程度的重要参数，对于研究晶体物理性质及合成新材料具有重要意义。

本文将介绍常见晶体空间利用率的计算方法。

晶体空间利用率的计算可以从两个角度出发：从输入晶体结构的角度，或者从晶胞的角度。

以下将分别对两种方法进行介绍。

1.从输入晶体结构的角度计算晶体空间利用率在这种方法中，需要输入晶体的原子或分子坐标，以及晶胞参数。

计算晶体空间利用率的一种常见方法是使用球形原子假设。

首先，计算晶胞中原子或分子的体积。

对于球形原子或分子，其体积可以通过球体积公式进行计算：V=4/3πr³，其中V为原子或分子体积，r为原子或分子的半径。

可以根据晶体结构中的原子或分子坐标，计算每个原子或分子的体积，并累加得到晶胞中原子或分子的总体积。

然后，计算晶胞的体积。

晶胞的体积可以通过晶胞参数计算得到。

对于立方晶胞，其体积可以简单地计算为晶胞参数的乘积。

对于其他类型的晶胞，可以使用相应的晶胞体积公式进行计算。

最后，将晶胞中原子或分子的总体积除以晶胞的体积，即可得到晶体的空间利用率。

2.从晶胞的角度计算晶体空间利用率在这种方法中，需要输入晶胞的晶胞参数，即晶胞的边长和角度。

首先，需要根据输入的晶胞参数，计算晶胞的体积。

对于正交晶体，晶胞的体积可以通过边长的乘积计算得到。

对于其他类型的晶胞，可以使用相应的晶胞体积公式进行计算。

然后，估算晶胞中原子或分子的体积。

可以使用球形原子假设，根据原子或分子的半径计算每个原子或分子的体积，并根据晶胞中的原子或分子数目进行累加，得到晶胞中原子或分子的总体积。

最后，将晶胞中原子或分子的总体积除以晶胞的体积，即可得到晶体的空间利用率。

需要注意的是，以上介绍的方法仅适用于球形原子或分子的情况。

对于非球形的原子或分子，空间利用率的计算更加复杂，需要考虑原子或分子间的相互作用、晶胞对称性等因素。

金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中，给出了金属晶体四种堆积方式的晶胞空间利用率。

空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。

下面就金属晶体的四种堆积方式计算晶胞的空间利用率。

一、简单立方堆积：在简单立方堆积的晶胞中，晶胞边长a等于金属原子半径r的2倍，晶胞的体积V晶胞=(2r)3。

晶胞上占有1个金属原子，金属原子的体积V原子=4πr3/3 ，所以空间利用率V原子/V晶胞 = 4πr3/ （3×(2r)3）=52.33﹪。

二、体心立方堆积：在体心立方堆积的晶胞中，体对角线上的三个原子相切，体对角线长度等于原子半径的4倍。

假定晶胞边长为a ，则a2 + 2a2 = (4r)2， a=4 r/√3 ，晶胞体积V晶胞 =64r3/ 3√3 。

体心堆积的晶胞上占有的原子个数为2，原子占有的体积为V原子=2×（4πr3/3）。

晶胞的空间利用率等于V原子/V晶胞 =（2×4πr3×3√3）/（3×64r3）= 67.98﹪。

三、面心立方最密堆积在面心立方最密堆积的晶胞中，面对角线长度是原子半径的4倍。

假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。

面心立方堆积的晶胞上占有的原子数为4，原子占有的体积为V原子 = 4×（4πr3/3）。

晶胞的空间利用率等于V原子/V晶胞 =（4×4πr3）/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。

晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形，边长a = 2r ,夹角分别为60°、120°，底面积s = 2r×2r×sin(60°) 。

六方最密堆积晶胞空间利用率计算六方最密堆积晶胞空间利用率计算是晶体学中的一种重要计算。

它可以帮助我们确定晶体的空间结构，从而实现最有效的流体流动。

一、定义：
六方最密堆积晶胞空间利用率是指在某种物理结构空间中，每个晶胞最多能容纳多少个原子，以及每个原子能占用多大空间的计算方式。

二、计算公式：
六方最密堆积晶胞空间利用率的计算公式为：六方最密堆积晶胞空间利用率=（原子数/晶胞最大容量）*100％。

三、实施过程：
（1）计算晶胞最大容量：首先，计算该晶体的晶胞型号，比如六方晶体、立方晶体甚至多余晶体，晶胞的形状可能是正方体、长方体或多边形。

（2）计算原子数：其次，统计该晶体中实际存在的原子数，包括离子式原子，共价键原子，以及成簇原子，计算出总的原子数。

（3）最后，用公式计算即可得出该晶体的六方最密堆积晶胞空间利用
率。

四、预期结果：
通过六方最密堆积晶胞空间利用率的计算，可以得出某一晶体的晶胞利用率，即介绍反映其空间结构的一份重要的定量报告。

它可以帮助我们了解晶体的实际状态，如特定空间布局，原子位置等，从而实现最有效的流体流动。

六方最密堆积晶胞空间利用率计算为了计算六方最密堆积晶胞的空间利用率，我们首先需要了解晶胞的构成和排列方式。

六方最密堆积晶胞由最密堆积的球体构成，每个球体的圆心与它周围六个球体的圆心相接触，形成一个六边形排列。

在六方最密堆积晶胞中，每个晶胞都由两个六方紧密堆积平面和一个六方紧密堆积间隙填充而成。

六方紧密堆积平面的排列方式是ABAB...，每两个平面之间间隔一个六方紧密堆积间隙。

每个六方紧密堆积间隙由三个边长等于晶胞边长的球体填充。

我们可以通过计算晶胞中球体所占的体积来计算空间利用率。

对于一个六方最密堆积晶胞，其中的三个球体构成了一个等边三角形。

我们可以将这个等边三角形划分为两个等腰直角三角形，每个直角三角形的底边长度等于晶胞的边长，高等于底边长度的一半。

根据直角三角形的面积公式，我们可以计算出一个直角三角形的面积为S = 0.5 * base * height = 0.5 * a * (a/2) = (a^2)/4，其中a为晶胞的边长。

由于晶胞中共有两个等腰直角三角形，所以晶胞中球体所占的总体积为V = 2 * S = (a^2)/2晶胞的体积为V_cell = a^3，所以六方最密堆积晶胞的空间利用率可以表示为：Utilization = V / V_cell = ((a^2)/2) / (a^3) = 1 / (2a)根据上述计算公式，我们可以得到六方最密堆积晶胞的空间利用率。

这个数值表示了晶体中实际占据的体积与晶胞总体积之间的比例。

六方最密堆积晶胞的空间利用率比较高，可以达到50%。

这也是为什么这种晶体结构在材料科学和工程中有着广泛应用的原因之一总之，六方最密堆积晶胞的空间利用率是晶胞中球体所占的体积与晶胞总体积之间的比例。

它是计算晶体结构密排程度的一种指标，也可以帮助我们理解晶体的物理特性和力学性能。

晶胞空间利用率教学设计导语：晶体结构是材料科学中非常重要的一部分，因为它们的结构直接决定了材料的性能和用途。

了解晶胞空间利用率的概念和计算方法，对于学生深入理解材料科学具有重要的意义。

本文将介绍一个教学设计，旨在帮助学生理解晶胞空间利用率的概念并掌握其计算方法。

一、教学目标1.了解晶体结构中晶胞的概念和作用；2.理解晶胞的空间利用率概念；3.掌握计算晶胞空间利用率的方法；4.能够运用所学知识解决相关实际问题。

二、教学步骤1.导入介绍晶体结构及其重要性，并引出晶胞的概念。

通过实例解释晶胞在晶体结构中的作用。

2.讲解晶胞的概念简要介绍晶胞的定义和特征，包括晶胞的形状、大小、组成等。

通过幻灯片或黑板画图示意，帮助学生直观理解晶胞的概念。

3.引入晶胞空间利用率通过实例引出晶胞空间利用率的概念，解释其意义和计算方法。

提问学生关于晶胞空间利用率的问题，引导学生思考晶胞空间利用率与晶体结构的关系。

4.计算晶胞空间利用率详细介绍晶胞空间利用率的计算方法，包括晶胞体积、原子或离子的体积等相关参数的计算。

通过例题演示计算过程，指导学生掌握计算方法。

5.应用实例提供一些实际问题，要求学生运用所学知识计算晶胞空间利用率并分析结果。

通过小组讨论和展示，培养学生的分析和解决问题的能力。

6.总结与拓展总结晶胞空间利用率的概念和计算方法，回顾教学内容，并给予学生一些拓展阅读材料，让他们对晶体结构和晶胞空间利用率有更深入的理解和应用。

三、教学评价1.课堂表现观察学生在课堂上的参与情况，包括回答问题的准确性、提出问题的质量、与同学的讨论等。

2.小组讨论展示评价小组在解决应用实例问题中的表现，包括计算准确性、分析合理性以及解决问题的方法。

3.作业和考试布置相应的作业和开展考试，检查学生对于晶胞空间利用率的掌握程度和能力。

四、教学资源1.教学课件或投影仪2.幻灯片或黑板3.实例题和习题4.拓展阅读资料总结：通过这个教学设计，学生将能够深入理解晶胞空间利用率的概念和计算方法，在实践应用中培养他们的问题解决能力和创新思维。