当前位置：文档之家 › 新课标高考物理二轮复习宇宙多星系统模型课件

新课标高考物理二轮复习宇宙多星系统模型课件

  • 格式：ppt
  • 大小：641.50 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

新人教高中物理必修二6.5宇宙航行第二课时 课件 (共22张PPT)

新人教高中物理必修二6.5宇宙航行第二课时 课件 (共22张PPT)

【例题】 (多选)如图所示,甲、乙、丙是位于同
一直线上的离其他恒星较远的三颗恒星, 甲、丙围
绕乙在半径为R的圆轨道上运行.若三颗星质量均为
M,万有引力常量为G,则( )
A. 甲星所受合外力为
5G M 2 4R 2来自B. 乙星所受合外力为 G M 2
R2
C. 甲星和丙星的线速度相同 D. 甲星和丙星的角速度相同
思考：人造卫星在低轨道上运行，要想让其
在高轨道上运行，应采取什么措施？
三、变轨
卫星变轨原理
V mA
F引
F引
G
Mm r2
F引＜F向 F引＞F向
F引 F向
F向
m
v2 r
M
在A点万有引力相同
A点速度—内小外大（在A点看轨迹）
卫星变轨原理
思考：人造卫星在低轨道上运行，要想让其在 高轨道上运行，应采取什么措施？
。2021年3月18日星期四2021/3/182021/3/182021/3/18
• 15、会当凌绝顶，一览众山小。2021年3月2021/3/182021/3/182021/3/183/18/2021
• 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/3/182021/3/18March 18, 2021
对接方法：
• 飞船首先在比空间站低的轨道运 行，当运行到适当位置时，再加 速运行到一个椭圆轨道。
• 通过控制轨道使飞船跟空间站恰 好同时运行到两轨道的相切点， 此时飞船适当减速，便可实现对 接，如图示。
空间站
飞船
2、宇宙飞船和轨道空间站在同一轨道上运动， 若飞船想与前面的空间站对接，飞船为了 追上轨道空间站，可采取的方法是： ( )

2019届二轮复习 微专题3 宇宙双星及多星系统模型 课件(23张)

2019届二轮复习 微专题3 宇宙双星及多星系统模型 课件(23张)

速度相同，故vr11＝vr22，即vv21＝rr12＝mm21，B错误；
首页 上页 下页 尾页
A星受到B星的引力为F＝G
m1m2 d2
，等效为放在O点的星体对A
星的引力为F′＝G
m1m′ r21
，有G
m1m2 d2
＝G
m1m′ r21
，代入r1＝
m2 m1＋m2
d可得m′＝
m32 m1＋m22
m1ω12r1，GmL12m2＝m2ω22r2. (2)两颗星的周期及角速度都相同，即T1＝T2，ω1＝ω2. (3)两颗星的半径与它们之间的距离关系为：r1＋r2＝L. (4)两颗星到圆心的距离r1、r2与星体质量成反比，即mm21＝rr21.
首页 上页 下页 尾页
[应用提升练] 1．银河系的恒星中大约四分之一是双星系统，某双星系统 由质量不等的星体S1和S2构成，两星在相互间的万有引力作 用下绕两者连线上某一点C做匀速圆周运动．由天文观察测 得其运行周期为T，S1到C点的距离为r1，S2的质量为m，已 知引力常量为G，由此可求出两星间的距离r及两星的总质量 M分别为( )
量为m′的星体对它的引力，则m′＝
m32 m1＋m22
D．若在O点放一个质点，则此质点受到的合力一定为零
首页 上页 下页 尾页
[思路探究] (1)A星和B星做匀速圆周运动所需的向心力来源 是什么？ (2)万有引力公式F＝GMr2m中“r”指的是什么？ (3)A星和B星是否一直保持连线过“图中O点”？
m2 l2
，
对任一星受力分析，如图所示．由图中几
何关系和牛顿第二定律可得 3 F＝ma＝
mω2 l ，联立可得ω＝ 3
3Gm l3
，a＝ω2
l 3

新人教版高中物理必修二第六章第五节宇宙航行课件 (共51张PPT)

新人教版高中物理必修二第六章第五节宇宙航行课件 (共51张PPT)

4．梦想成真． 1957 年 10 月，苏联成功发射了第一颗人造地球卫星． 1969 年 7 月，美国“阿波罗 11 号”登上月球． 2003 年 10 月 15 日，我国航天员杨利伟踏入太空． 2010 年 10 月 1 日，我国的“嫦娥二号”探月卫星发 射成功． 2013 年 6 月 11 日，我国的“神舟十号”飞船发射成 功．
结合选项 C 知选项 D 错误．本题正确选项为 A、B、 C.
答案：ABC
2．(多选)三颗人造地球卫星 A、B、C 绕地球做匀速 圆周运动，如图所示，已知 mA＝mB＜mC，则对于三颗卫 星，正确的是( )
A．运行线速度关系为 vA＞vB＝vC B．运行周期关系为 TA＜TB＝TC
C．向心力大小关系为 FA＝FB＜FC D．半径与周期关系为RT2A3A＝RT2B3B＝RT2C3C 解析：由 GMr2m＝mvr2得 v＝ GrM，所以 vA＞vB＝
1.第一宇宙速度的理解. 2.人造卫星的线速度、角 速度、周期与半径的关 系.
知识点 宇宙航行
提炼知识 1．牛顿的“卫星设想”． 如图所示，当物体的初速度足够大时， 它将会围绕地球旋转而不再落回地面，成为 一颗绕地球转动的人造卫星．
2．原理． 一般情况下可认为人造地球卫星绕地球做匀速圆周 运动，向心力由地球对它的万有引力提供，即 GMr2m＝_m_v_r2，
1．人造卫星的 an、v、ω、T 由地球的质量 M 和卫星 的轨道半径 r 决定，当 r 确定后，卫星的 an、v、ω、T 便 确定了，与卫星的质量、形状等因素无关，当人造卫星的 轨道半径 r 发生变化时，其 an、v、ω、T 都会随之改变．
2．在处理人造卫星的 an、v、ω、T 与半径 r 的关系 问题时，常用公式“gR2＝GM”来替换出地球的质量 M， 会使问题解决起来更方便．

多星系统模型(共32张PPT)

多星系统模型(共32张PPT)
通过转换研究对象,有时可转化为求恒力做功,可 以用W=Flcos α求解。此法常应用于轻绳通过定 滑轮拉物体的问题中。
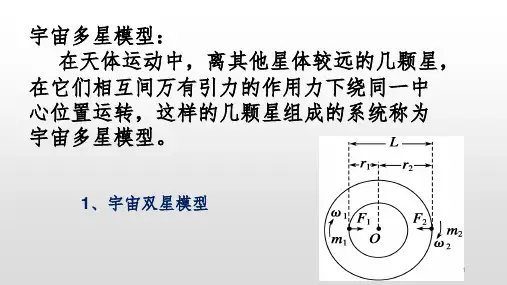
例5(微元法)如图所示,在水平面上,有一弯曲的槽道AB,槽道由半径分别为 R/2 和R的两个半圆构成。 例5(微元法)如图所示,在水平面上,有一弯曲的槽道AB,槽道由半径分别为 R/2 和R的两个半圆构成。 三颗行星始终位于同一直线上，中心行星受力平衡，其余两颗行星的引力提供向心力：
例3(图象法)一物体所受的力F随位移x变化的图象如图所示, 求在这一过程中,力F对物体做的功为多少?
例4(图像法)用锤子击打钉子,设木板对钉子的阻力跟钉子进入 木板的深度成正比,每次击打钉子时锤子对钉子做的功相同。已知第 一次击打钉子后,钉子进入的深度为1 cm,则第二次击打时,钉子进 入的深度是多少?
已知第一次击打钉子后,钉子进入的深度为1 cm,则第二次击打时,钉子进入的深度是多少? （2）三颗质量相等的行星位于三角形的三个顶点上，另一颗恒星位于三角形的中心o点，三颗行星以o点为圆心。 已知第一次击打钉子后,钉子进入的深度为1 cm,则第二次击打时,钉子进入的深度是多少? 质点自P滑到Q的过程中,克服摩擦力所做的功为？ 两行星转动的方向相同，周期、角速度、线速度的大小相等
现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时刻与小球运动方向一致,则此过程中拉力所做的功为 （1）四颗质量相等的行星位于正方形的四个顶点上，沿外接于正方形的圆轨道做匀速圆周运动
阻力f
kx
k
2 1
1 cm x
1区面积与2区面积相等 k/2=(k+kx)(x-1)/2
深度x
4.利用微元法求变力做功
将物体的位移分割成许多小段,因小段很小,每一小段上作用

高中物理必2课件：6.5 宇宙航行课件

高中物理必2课件：6.5 宇宙航行课件
简称 人造卫星。 学.科.网
由此可见，人造地球卫星运行遵 循的规律是：卫星绕地球做圆周运动，
地球对卫星的引力就是向心力。
想一想:卫星运动快慢跟什么有 关呢?
（二）卫星的绕行速度、角速度、周期和轨道半径的关系
1、线速度随轨道半径的关系：
GMm mV2
r2
r
V
GM r
可见：卫星绕行轨道半径越大，绕行速度越小。
各种各样的卫星……
思考：卫星的轨道 北
西
F
赤道平面
东
F
南
人造地球卫星的运行轨道
卫星绕地球做匀速圆周运动时，是地球的引力提供 向心力，卫星受到地球的引力方向指向地心，而做圆 周运动的向心力方向始终指向圆心，所以卫星圆周运 动的圆心和地球的地心重合。这样就存在三类人造地 球卫星轨道：
①赤道轨道，卫星轨道在赤道平面， 卫星始终处于赤道上方； ②极地轨道，卫星轨道平面与赤道 平面垂直，卫星通过两极上空； ③一般轨道，卫星轨道和赤道成
对第一宇宙速度的理解:
v1
GM R
gR
1.上式对其它天体也适用，R为天体半径, M为 天 体质量, g为天体表面的重力加度,G为引力 常量. 2.v1为发射卫星的最小发射速度,又是卫星进入
？ 轨道后最大线速度(也叫运行速度).
人造卫星的发射速度与运行速度
1、发射速度是指被发射物在地面附近离开发射装置时的 速度,并且一旦发射就再也没有补充能量,被发射物仅依 靠自身的初动能克服地球引力做功上升一定高度,进入 运行轨道.因卫星上升过程中要克服引力和空气阻力(在 大气层中时)做功消耗动能,所以卫星越高,发射速度越大。
v gR 二、宇宙速度
GM
1.第一宇宙对任何天体都适用）

新人教版物理必修2高中物理新课标第六章第五节比赛宇宙航行教学课件 (共18张PPT)

新人教版物理必修2高中物理新课标第六章第五节比赛宇宙航行教学课件 (共18张PPT)

• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
高中物理新课标人教版物理必修2
第六章
万户是世界上公认的“第一个尝试利用 火箭进行飞行的人”。为表彰他的功绩，国 际天文联合会将月球上的一座环形山命名为 “万户”。
已知
M地=5.98×1024 kg R地=6.40×106m，
求：V
R
练习：求近地卫星的周期
T 2 r3
GM 地
23.14
(6.37 106 )3 6.671011 5.981024 s
•
THE END 17、一个人如果不到最高峰，他就没有片刻的安宁，他也就不会感到生命的恬静和光荣。2021/3/172021/3/172021/3/172021/3/17
谢谢观看Biblioteka • 10、人的志向通常和他们的能力成正比例。2021/3/172021/3/172021/3/173/17/2021 4:26:27 PM • 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/3/172021/3/172021/3/17Mar-2117-Mar-21 • 12、越是无能的人，越喜欢挑剔别人的错儿。2021/3/172021/3/172021/3/17Wednesday, March 17, 2021 • 13、志不立，天下无可成之事。2021/3/172021/3/172021/3/172021/3/173/17/2021

2020届二轮复习 核心素养微专题3宇宙多星系统模型 课件(19张)

2020届二轮复习 核心素养微专题3宇宙多星系统模型 课件(19张)

A．四颗星圆周运动的轨道半径均为L2
B．四颗星圆周运动的线速度均为 C．四颗星圆周运动的周期均为2π
GLm2＋ 42
2L3 4＋ 2Gm
D．四颗星表面的重力加速度均为GRm2
解析：如图所示，四颗星均围绕正方形对角
线的交点做匀速圆周运动，轨道半径均为r＝
2 2
L.取任一顶点上的星体为研究对象，它受
m2 L2
cos
30°＝ma，得a＝ 3LG2m，D项正确.
[答案] BD
规律总结 宇宙多星模型特点
——————————————————————————— (1)天体运动中，三星、四星等多星模型是指相互作用且围绕 某一点做圆周运动的星体． (2)星体做圆周运动所需向心力由其他星体对它的万有引力的 合力提供，在多星系统中各星体运行的角速度相等．
G
m2 l2
，故选项A正确；由牛顿第二定律

G
m2 l2
＝ma可得a＝
3Gm l2
，故选项B错误；由
3
G
m2 l2
＝m
4π2r T2
，r＝
33 l可得T＝2π
3Gl3m，当l和m都变为原来的2倍，则周期变为原来的2倍，
选项C正确；由速度公式可得v＝
2πr T
＝
Gm l
，当l和m都变
为原来的2倍，则线速度不变，选项D错误．
(1)A星体所受合力大小FA； (2)B星体所受合力大小FB； (3)C星体的轨道半径RC； (4)三星体做圆周运动的周期T.
解析：(1)由万有引力定律，A星体
所受B、C星体引力大小为FBA＝
G
mAmB r2
＝G
2m2 a2
＝FCA，方向如图

宇宙多星系统模型PPT课件

宇宙多星系统模型PPT课件
6
(1)三星同线模型 ①如图所示，三颗质量相等的行星，一颗行星位于中心位
置不动，另外两颗行星围绕它做圆周运动。这三颗行星始终位
于同一直线上，中心行星受力平衡。运转的行星由其余两颗行 星的引力提供向心力：Grm2 2＋G2mr22＝ma 向
两行星运行的方向相同，周期、角 速度、线速度的大小相等。
7
②如图所示，三颗质量相等的行星位于一正三角形的顶点处， 都绕三角形的中心做圆周运动。每颗行星运行所需向心力都由其 余两颗行星对其万有引力的合力来提供。
宇宙多星模型： 在天体运动中，离其他星体较远的几颗星，
在它们相互间万有引力的作用力下绕同一中 心位置运转，这样的几颗星组成的系统称为 宇宙多星模型。
1、宇宙双星模型
1
2．双星系统模型问题的分析与计算
绕公共圆心转动的两个星体组成的系统，我们称之为双星系统，如图 6 所示，双星 系统模型有以下特点：
(1)各自需要的向心力由彼此间的万有引力相互提供，即
为G。(1)分析说明三绕一应该具有怎样的空间结构模式
(2)若相邻星球的最小距离均为a,求两种构成形式下天体运
动的周期之比
12
解析:(1)三颗星绕另一颗中心星运动时,其中任意一个绕行星球受 到另三个星球的万有引力的合力提供向心力,三个绕行星球的向心 力一定指向同一点,且中心星受力平衡,由于星球质量相等,具有对 称关系,因此向心力一定指向中心星,绕行星一定分布在以中心星为 重心的等边三角形的三个顶点上,如图甲所示。
明理由并写出你认为正确的结果。
10
解析:星体做圆周运动所需的向心力靠其他两个星体的万有引力的合
力提供,求两星体之间的万有引力时,应用星体之间的距离r,①③式正 确。正确解法为:

高中物理必修二课件-6.5宇宙航行23-人教版

高中物理必修二课件-6.5宇宙航行23-人教版
旋转绕而足地不够球大再转落动回的地__球__表__面__，__成__为_．一颗
人造地球卫星
2．原理：一般情况下可认为人造地球卫星绕地 球做_匀__速__圆__周__运动，向心力由地球对它的 Mm _万__有__引__力__提供，即_G___r_2 ___＝
图6－5－1
mvr2，则卫星在轨道上运行的线速度
T＝2π GrM3 ，r 越大，T 越大，
a＝GrM2 ，r 越大，a 越小．
•决注定意，：与地卫球星卫的星质的量an、、形v、状ω等、因T由素地无球关的．质量M和卫星的轨道半径r
【例3】a、b、c、d是在地球大
气层外的圆形轨道上运行的四颗
人造卫星．其中a、c的轨道相交 于P，b、d在同一个圆轨道上，b、 c轨道在同一平面上．某时刻四 颗卫星的运行方向及位置如图6 －5－3所示，下列说法中正确的
5.宇宙航行
[目标定位] 1.知道三个宇宙速度的含义，会推导第一宇宙速 度的公式．
2．理解掌握人造卫星的线速度、角速度、周期、向心加速度 与轨道半径的关系．
3．了解人造卫星的相关知识及我国卫星发射的情况，激发学 生的爱国热情．
• 一、人造地球卫星
1. 牛顿的设想：如图6－5－1所示，
在高山上水平抛出一物体，当物体的 初速度_______时，它将会围绕地球
图6－5－2
(2)特点：所有的轨道圆心都在地心．
• 2．处理思路及规律
将人造卫星视为绕地球(或其他天体)做匀速圆 周运动，所需向心力等于地球(或其他天体)对卫星的
万有引力，即：
GMr2m＝mvr2＝mω2r＝m2Tπ2r＝man.
所以 v＝ GrM，r 越大，v 越小，
ω＝ GrM3 ，r 越大，ω越小，

人教版(新教材)高中物理必修2：第4节 宇宙航行ppt课件

人教版(新教材)高中物理必修2：第4节 宇宙航行ppt课件
答案 AC
三、载人航天与太空探索
1961年4月12日，苏联航天员加加林进入了东方一号载人飞船。 1969年7月16日9时32分，运载阿波罗11号飞船的土星5号火箭在美国卡纳维拉尔 角点火升空，拉开人类登月这一伟大历史事件的帷幕。 2003年10月15日9时，我国_神__舟__五__号___宇宙飞船把中国第一位航天员杨利伟送入 太空。 2013年6月，神舟十号分别完成与天宫一号空间站的手动和自动交会对接。 2016年10月19日，神舟十一号完成与天宫二号空间站的自动交会对接。 2017年4月20日，我国又发射了货运飞船天舟一号，入轨后与天宫二号空间站进 行自动交会对接、自主快速交会对接等3次交会对接及多项实验。
二、人造地球卫星 1.1957年10月4日，世界上第一颗人造地球卫星发射成功。 1970年4月24日，我国第一颗人造卫星“__东__方__红__一__号__”发射成功。 2.地球同步卫星
(1)概念：相对于地面静止且与地球自转具有相同_周__期___的卫星，叫作地球同步卫 星。
(2)特点：六个“一定” ①转动方向一定：和地球自转方向__一__致__； ②周期一定：和地球自转周期相同，即T＝24 h； ③角速度一定：等于地球自转的角速度； ④轨道平面一定：所有的同步卫星都在赤道的__正__上__方__，其轨道平面必须与赤 道平面重合； ⑤高度一定：离地面高度固定不变(约3.6×104 km)； ⑥速率一定：线速度大小一定(约3.1×103 m/s)。
■归纳拓展
1.第一宇宙速度：第一宇宙速度是人造卫星近地环绕地球做匀速圆周运动的速度。 2.第一宇宙速度的计算式
(1)由 GMRm2 ＝mvR2推导可得_v__＝____G_R_M___。 也适用于其他星体的卫星 (2)由 mg＝mvR2推导可得__v_＝___g_R___。

宇宙多星系统模型资料讲解

宇宙多星系统模型资料讲解

[解析] 设两颗星的质量分别为m1、m2，做圆周运动
的半径分别为r1、r2，根据万有引力提供向心力可得： Grm1＋1mr222＝m1r14Tπ22，Grm1＋1mr222＝m2r24Tπ22，联立解得：m1＋ m2＝4π2Gr1T＋2 r23，即T2＝4Gπ2mr11＋＋mr223，因此，当两星总质量
(5)双星的运动周期 T＝2π
L3 Gm1＋m2
(6)双星的总质量公式 m1＋m2＝4Tπ22GL3
[典例 1] 冥王星与其附近的星体卡戎可视为双星系统，它们的质量
比约为 7∶1，同时绕它们连线上某点 O 做匀速圆周运动．由此可知
卡戎绕 O 点运动的 ( )
CD
A．角速度大小约为冥王星的 7 倍
B．向心力大小约为冥王星的 1/7 C．轨道半径约为冥王星的 7 倍
T22 2
解得T2=2
4(4④ 2) 2a3
7Gm
故 T1 = (4 。 2)(3 3)
T2
4
(1)各自需要的向心力由彼此间的万有引力相互提供，即
GmL12m2＝m1ω1 2r1，GmL12m2＝m2ω2 2r2
(2)两颗星的周期及角速度都相同，即 T1＝T2，ω1＝ω2
(3)两颗星的半径与它们之间的距离关系为：r1＋r2＝L
(4)两颗星到圆心的距离 r1、r2 与星体质量成反比，即mm12＝rr21
做周期相同的匀速圆周运动。研究发现，双星系统演化过
程中，两星的总质量、距离和周期均可能发生变化。若某
双星系统中两星做圆周运动的周期为 T，经过一段时间演
化后，两星总质量变为原来的 k 倍，两星之间的距离变为
原来的 n 倍，则此时圆周运动的周期为
()
n3

《宇宙双星模型》课件

《宇宙双星模型》课件
2023
《宇宙双星模型》 ppt课件
REPORTING
2023
目录
• 双星模型简介 • 双星系统的运动规律 • 双星模型在天文学中的应用 • 双星模型的研究前景与挑战 • 总结与展望
2023
PART 01
双星模型简介
REPORTING
定义与概念
总结词
双星模型是指由两个恒星组成的相对稳定的系统，它们通过引力相互作用，围 绕彼此旋转。
双星演化理论的完善
虽然已经建立了一套相对完善的双星演化理论，但随着观 测数据的不断增多和理论研究的不断深入，需要进一步完 善双星演化理论。
2023
PART 05
总结与展望
REPORTING
双星模型的意义与价值
理论意义
双星模型在天文学中具有重要的理论 意义，它为研究恒星演化、星系形成 和演化等提供了重要的理论基础。
双星系统中的两颗恒星通过相互吸引和旋转，形成稳定的双星结构。在星系形成 过程中，双星系统可以聚集周围的物质，形成更大的恒星群或行星系统，从而影 响整个星系的形状和演化。
双星在恒星演化中的作用
总结词
双星在恒星演化中起到关键作用，它们通过相互作用加速恒 星的演化进程。
详细描述
在双星系统中，两颗恒星之间存在相互作用，如物质交换和 轨道扰动等，这些作用可以加速恒星的演化进程。例如，双 星中的一颗恒星可能因为吸收了另一颗恒星的物质而迅速膨 胀，最终导致超新星爆发。
详细描述
双星模型是研究恒星系统的一个重要概念，它涉及到两个恒星在相互引力的作 用下，形成一个相对稳定的系统。这两个恒星可以是类似太阳的恒星，也可以 是其他类型的天体，如白矮星、中子星等。
双星系统的形成
总结词
双星系统的形成通常发生在恒星形成过程中，当两颗恒星在引力作用下逐渐靠近，最终形成一个双星系统。

2019年高考物理二轮专题复习：专题10 卫星变轨、双星模型课件

2019年高考物理二轮专题复习：专题10 卫星变轨、双星模型课件

02
典例精析
多星模型 (1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央 星体外，各星体的角速度或周期相同. (2)三星模型：
①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨
道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示).
爆发现象.在利用“慧眼”观测美丽的银河系时，若发现某双黑洞间的距离
为L(黑洞的半径远小于黑洞之间的距离)，只在彼此之间的万有引力作用下
做匀速圆周运动，其运动周期为T，引力常量为G，则双黑洞总质量为 ( A )
4π2L3 A. GT2
4π2L3 B.3GT2
GL3 C.4π2T2
4π2T3 D. GL2
(4)机械能：在一个确定的圆(椭圆)轨道上机械能守恒.若卫星在Ⅰ、Ⅱ、Ⅲ
轨道的机械能分别为E1、E2、E3，则E1<E2<E3.
01 模型
构建
考向认知
能力考点 师生共研
1.双星模型 (1)定义：绕公共圆心转动的两个星体组成的系统，我们称之为双星系统， 如图所示. (2)特点： ①各自所需的向心力由彼此间的万有引力相互提供，即 GmL12m2＝m1ω 12r1，GmL12m2＝m2ω 22r2 ②两颗星的周期及角速度都相同，即
确
；
由
开
普
勒
第
三
定
律
有
[12r1＋r2]3 2t2
＝
r31 T2
，
得
r1＋r2T t ＝ 4r1
r1＋r2 2r1 ，所以 B 错误；卫星在椭圆轨道中运行时，机械能是
守恒的，所以 C 错误；卫星从圆轨道进入椭圆轨道过程中在 A

高考物理二轮复习核心素养微专题3宇宙双星与多星问题课件

高考物理二轮复习核心素养微专题3宇宙双星与多星问题课件

模型 2 如图 2 所示，三颗质量相等的行星位于一正三角形的顶点处，都 绕三角形的中心做圆周运动。每颗行星运行所需向心力都由其余两颗行 星对其万有引力的合力来提供，即GLm2 2×2×cos 30°＝ma 向，其中 L＝ 2rcos 30°。三颗行星运行的方向相同，周期、角速度、线速度的大小相 等。
2．特点 (1)各自所需的向心力由彼此间的万有引力提供，即GmL12m2＝m1ω12r1， GmL12m2＝m2ω22r2。 (2)两颗星的周期及角速度都相同，即 T1＝T2，ω1＝ω2。 (3)两颗星的半径与它们之间的距离关系为 r1＋r2＝L。 (4)两颗星到圆心的距离 r1、r2 与星体质量成反比，即mm21＝rr21。
A．质量之积
B．质量之和
C．速率之和
D．各自的自转角速度
[解析] 两颗中子星运动到某位置的示意图如图所示。 每秒转动 12 圈，角速度已知， 中子星运动时，由万有引力提供向心力得
Gml21m2＝m1ω2r1
①
Gml21m2＝m2ω2r2
②
l＝r1＋r2
③
由①②③式得G（m1l＋2 m2）＝ω2l，所以 m1＋m2＝ωG2l3，
A．直线三星系统中甲星和丙星的线速度相同
B．直线三星系统的运动周期 T＝4πR
R 5GM
3 C．三角形三星系统中星体间的距离 L＝
12 5R
D．三角形三星系统的线速度大小为12
5GM R
[解析] 直线三星系统中甲星和丙星的线速度大小相同，方向相反，选项 A 错误；三星系统中，对直线三星系统有 GMR22＋G（2MR2）2＝M4Tπ22R，解
2. (2020·江西七校联考)宇宙中，两颗靠得比较近的恒星，只受到彼此之 间的万有引力作用，分别围绕其连线上的某一点做周期相同的匀速圆周 运动，称之为双星系统。由恒星 A 与恒星 B 组成的双星系统绕其连线上 的 O 点做匀速圆周运动，如图所示。已知它们的运行周期为 T，恒星 A 的质量为 M，恒星 B 的质量为 3M，引力常量为 G，则下列判断正确的 是( A )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

7 4 a.
60°＝ 3
(或由对称性可知OB＝OC＝RC，cos
∠OBD＝
FBx FB
＝
DB OB
＝
1 R2aC，得RC＝ 47a)． (4)三星体运动周期相同，对C星体，由FC＝FB＝
7
G
m2 a2
＝
m(2Tπ)2RC，可得T＝π
a3 Gm.
答案：(1)2
m2 3G a2
m2 (2) 7G a2
[应用提升练] 1．(多选)宇宙间存在一些离其他恒 星较远的三星系统，其中有一种三星 系统如图所示，三颗质量均为m的恒 星分别位于等边三角形的三个顶点 上，三角形边长为l，忽略其他星体 对它们的引力作用，三星在同一平面内绕三角形中心O做匀速 圆周运动，引力常量为G，下列说法正确的是( )
A．每颗星所受的万有引力为
G
m2 l2
，故选项A正确；由牛顿第二定律
3
G
m2 l2
＝ma可得a＝
3Gm l2

4π2r T2
，r＝
33 l可得T＝2π
3Gl3m，当l和m都变为原来的2倍，则周期变为原来的2倍，
选项C正确；由速度公式可得v＝
2πr T
＝
Gm l
，当l和m都变
为原来的2倍，则线速度不变，选项D错误．
宇宙多星系统模型
C目录 ONTENTS
科学思维
在宇宙中有一些彼此较近，而离其他星较远的几颗星组成的 孤立行星系统，称为多星系统，这类系统具有研究对象多 个、运动模型多样、受力情况复杂、科技联系密切等特点， 备受高考命题者青睐．对于这类问题，解题的关键是弄清运 动模式，确定好角速度、周期、轨道半径等数量关系．
m2 3G l2
B．每颗星做圆周运动的加速度与三星的质量无关
C．若距离l和每颗星的质量m都变为原来的2倍，则周期变为
原来的2倍
D．若距离l和每颗星的质量m都变为原来的2倍，则线速度变
为原来的4倍
解析：任意两星间的万有引力F＝G
m2 l2
，对任一星受力分析，
如图所示．由图中几何关系可得每颗星所受的万有引力为 3
FAB＝GmArm2 B＝G2am22，
FCB＝GmCrm2 B＝Gma22，方向如图所示．
由FBx＝FABcos
60°＋FCB＝2G
m2 a2
，FBy＝FABsin
Gma22，可得FB＝
F2Bx＋F2By＝
m2 7G a2 .
(3)通过分析可知，圆心O在中垂线AD的中点，则
RC＝
43a2＋12a2，可得RC＝
[示例] (多选)宇宙中存在一些离其他恒星较远的三星系统， 通常可忽略其他星体对它们的引力作用，三星质量相同．现 已观测到稳定的三星系统存在两种基本的构成形式：一种是 三颗星位于同一直线上，两颗星围绕中央星做圆周运动，如 图甲所示；另一种是三颗星位于等边三角形的三个顶点上， 并沿外接于等边三角形的圆形轨道运行，如图乙所示．设两 种系统中三个星体的质量均为m，且两种系统中各星间的距离 已在图甲、图乙中标出，引力常量为G，则( )
m2 L2
cos
30°＝ma，得a＝ 3LG2m，D项正确.
[答案] BD
规律总结 宇宙多星模型特点
——————————————————————————— (1)天体运动中，三星、四星等多星模型是指相互作用且围绕 某一点做圆周运动的星体． (2)星体做圆周运动所需向心力由其他星体对它的万有引力的 合力提供，在多星系统中各星体运行的角速度相等．
答案：CD
3．由三颗星体构成的系统，忽略其 他星体对它们的作用，存在着一种运 动形式，三颗星体在相互之间的万有 引力作用下，分别位于等边三角形的 三个顶点上，绕某一共同的圆心O在 三角形所在的平面内做相同角速度的圆周运动(图示为A、B、 C三颗星体质量不相同时的一般情况)．若A星体质量为2m， B、C两星体的质量均为m，三角形的边长为a，求：
(1)A星体所受合力大小FA； (2)B星体所受合力大小FB； (3)C星体的轨道半径RC； (4)三星体做圆周运动的周期T.
解析：(1)由万有引力定律，A星体
所受B、C星体引力大小为FBA＝
G
mAmB r2
＝G
2m2 a2
＝FCA，方向如图
所示，则合力大小为FA＝2
m2 3G a2 .
(2)同上，B星体所受A、C星体引力大小分别为
A．四颗星圆周运动的轨道半径均为L2
B．四颗星圆周运动的线速度均为 C．四颗星圆周运动的周期均为2π
GLm2＋ 42
2L3 4＋ 2Gm
D．四颗星表面的重力加速度均为GRm2
解析：如图所示，四颗星均围绕正方形对角
线的交点做匀速圆周运动，轨道半径均为r＝
2 2
L.取任一顶点上的星体为研究对象，它受
到相邻的两个星体与对角线上的星体的万有引力的合力为F合
＝
2
G
m2 L2
＋G
m2 2L2
.由F合＝F向＝m
v2 r
＝m
4π2 T2
·r，可解得v＝
GLm1＋ 42，T＝2π
4＋2L23Gm，故A、B项错误，C项
正确．对于星体表面质量为m0的物体，受到的重力等于万有 引力，则有m0g＝GmRm2 0，故g＝GRm2，D项正确．
(3) 47a
(4)π
a3 Gm
答案：AC
2．(多选)宇宙中存在一些质量相等且离其他恒星较远的四颗 星组成的四星系统，通常可忽略其他星体对它们的引力作 用．设四星系统中每个星体的质量均为m，半径均为R，四颗 星稳定分布在边长为L的正方形的四个顶点上，其中L远大于R. 已知引力常量为G.忽略星体自转效应，关于四星系统，下列说 法正确的是( )
A．直线三星系统中星体做圆周运动的线速度大小为
Gm L
B．直线三星系统中星体做圆周运动的周期为4π
L3 5Gm
C．三角形三星系统中每颗星做圆周运动的角速度为2
L3 3Gm
D．三角形三星系统中每颗星做圆周运动的加速度大小为
3Gm L2
[解析] 在直线三星系统中，星体做圆周运动的向心力由其他两星
对它的万有引力的合力提供，根据万有引力定律和牛顿第二定律，
有G
m2 L2
＋G
m2 2L2
＝m
v2 L
，解得v＝
1 2
5Gm L
，A项错误；由周期T＝
2πr v
知，直线三星系统中星体做圆周运动的周期为T＝4π
L3 5Gm
，
B项正确；同理，对三角形三星系统中做圆周运动的星体，有2G
m2 L2
cos 30°＝mω2·2cosL30°，解得ω＝
3Gm L3
，C项错误；由2G