定积分的几何应用(体积))

三角函数的定积分计算与旋转体体积应用在数学中，三角函数的定积分计算以及与旋转体体积的应用是一项重要的内容。

通过对三角函数的定积分计算，我们可以求解曲线与坐标轴所围成的面积、弧长以及旋转体的体积，具有广泛的实际应用价值。

本文将围绕这一主题展开论述。

一、三角函数的定积分计算三角函数包括正弦函数、余弦函数、正切函数等，它们在数学和物理等领域中的应用广泛。

在定积分计算中，我们常常需要求解三角函数的不定积分和定积分。

1. 不定积分对于三角函数的不定积分，我们可以运用一些基本的积分公式进行计算。

例如，正弦函数的不定积分公式为：∫sin(x)dx = -cos(x) + C其中，C为常数。

类似地，其他三角函数的不定积分公式可以通过类似的方法推导得到。

2. 定积分对于三角函数的定积分计算，我们常常需要根据具体的问题给出积分上下限，并利用一些定积分的性质进行计算。

以求解曲线 y = sin(x) 与 x 轴所围成的面积为例，我们可以将问题转化为计算以下定积分：∫[a,b]sin(x)dx其中，[a,b]表示积分的区间。

通过运用定积分的性质和三角函数的积分公式，我们可以求解出该定积分的值，从而得到曲线与坐标轴所围成的面积。

二、旋转体的体积应用三角函数的定积分计算不仅在求解曲线面积等几何问题中有应用，还可以用于解决旋转体体积的计算。

1. 单位圆的体积以单位圆为例，我们可以将其沿着 x 轴或 y 轴进行旋转，并通过计算旋转体的体积来求解单位圆的体积。

当单位圆沿 x 轴旋转时，我们可以将其看作是由曲线 y = sin(x) 与 x 轴所围成的旋转体。

对于曲线 y = sin(x) 与 x 轴所围成的旋转体，它的体积可以通过以下定积分进行计算：V = π∫[0,2π]sin^2(x)dx其中，[0,2π]表示旋转的区间。

通过对该定积分进行计算，我们可以得到单位圆的体积，进而应用于相关实际问题中。

2. 一般曲线的体积除了单位圆以外，我们还可以利用三角函数的定积分计算来求解其他曲线的旋转体体积。

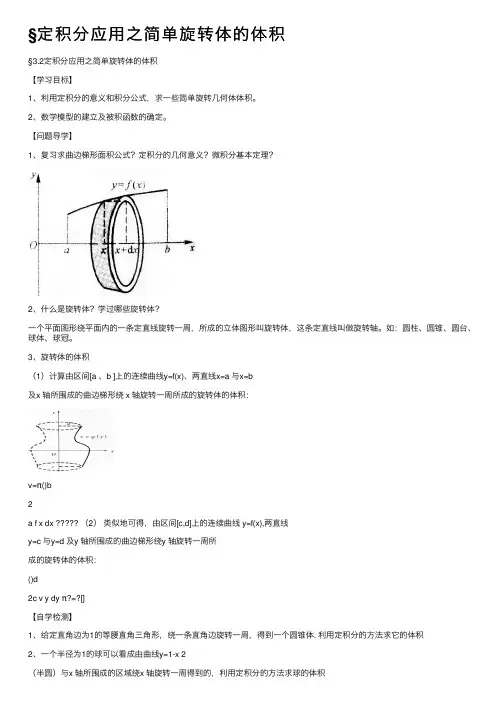
§定积分应⽤之简单旋转体的体积§3.2定积分应⽤之简单旋转体的体积【学习⽬标】1、利⽤定积分的意义和积分公式，求⼀些简单旋转⼏何体体积。

2、数学模型的建⽴及被积函数的确定。

【问题导学】1、复习求曲边梯形⾯积公式？定积分的⼏何意义？微积分基本定理？2、什么是旋转体？学过哪些旋转体？⼀个平⾯图形绕平⾯内的⼀条定直线旋转⼀周，所成的⽴体图形叫旋转体，这条定直线叫做旋转轴。

如：圆柱、圆锥、圆台、球体、球冠。

3、旋转体的体积（1）计算由区间[a 、b ]上的连续曲线y=f(x)、两直线x=a 与x=b及x 轴所围成的曲边梯形绕 x 轴旋转⼀周所成的旋转体的体积：v=π()b2a f x dx （2）类似地可得，由区间[c,d]上的连续曲线 y=f(x),两直线y=c 与y=d 及y 轴所围成的曲边梯形绕y 轴旋转⼀周所成的旋转体的体积：()d2c v y dy π?=?[]【⾃学检测】1、给定直⾓边为1的等腰直⾓三⾓形，绕⼀条直⾓边旋转⼀周，得到⼀个圆锥体. 利⽤定积分的⽅法求它的体积2、⼀个半径为1的球可以看成由曲线y=1-x 2（半圆）与x 轴所围成的区域绕x 轴旋转⼀周得到的，利⽤定积分的⽅法求球的体积3、求曲线y=e x 、x=0、x=12与x 轴围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积【当堂训练】4、求 y = x 2 与 y 2 = x 所围图形绕 x 轴旋转所成的旋转体体积5、将第⼀象限内由x 轴和曲线y 2=6x 与直线x=6所围成的平⾯图形绕x 轴旋转⼀周所得旋转体的体积等于6、求曲线x 轴、y 轴及直线x=1围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积7、求曲线y=1x、x=1、x=2 与x 轴围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积8、求曲线x=1与坐标轴围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积§3.2定积分应⽤之简单旋转体的体积1、3π2、43π3、(1)2e π-4、310π5、108π6、32π7、2π8、2π。

定积分的几何应用定积分是微积分中的重要概念，它有着广泛的应用。

其中之一就是在几何学中的应用。

本文将探讨定积分在几何学中的具体应用，并解释其背后的原理和意义。

一、平面图形的面积通过定积分，我们可以计算出复杂平面图形的面积。

假设有一个曲线方程y=f(x)，该曲线与x轴所围成的图形为A。

我们可以将A分解成无限个极小的矩形条，然后通过求和的方式来逼近A的面积。

具体而言，我们可以将横轴x划分为n个小区间，每个小区间的宽度为Δx。

然后，在每个小区间中，选择一个x值作为代表点，记作xi。

根据代表点xi和函数f(x)的值，我们可以计算出相应小矩形的高度为f(xi)。

由于每个小矩形的宽度Δx非常小，因此在计算总面积时，可以通过求和的方式逼近。

即可以得到如下的定积分表达式：A = ∫[a,b] f(x) dx其中[a,b]表示x的取值范围。

通过对上述定积分进行求解，即可得到图形A的面积。

二、曲线的弧长除了计算平面图形的面积外，定积分还可以用来计算曲线的弧长。

假设有一个曲线L，其方程为y=f(x)。

我们希望计算出曲线L的弧长。

与计算面积类似，我们同样可以将曲线L分解为无限个极小的线段，然后通过求和的方式来逼近曲线L的弧长。

具体而言，我们可以将横轴x划分为n个小区间，每个小区间的宽度为Δx。

然后，在每个小区间中，选择一个x值作为代表点，记作xi。

根据代表点xi和函数f(x)的值，我们可以计算出相应线段的长度为Δs。

同样地，由于每个小线段的长度Δs非常小，因此在计算总弧长时，可以通过求和的方式逼近。

即可以得到如下的定积分表达式：L = ∫[a,b] √(1 + [f'(x)]^2) dx其中[a,b]表示x的取值范围，f'(x)表示函数f(x)的导数。

通过对上述定积分进行求解，即可得到曲线L的弧长。

三、体积与质量除了平面图形的面积和曲线的弧长外，定积分还可以用来计算体积和质量。

当我们需要计算一个曲线绕某个轴旋转一周所形成的立体的体积时，定积分就派上用场了。

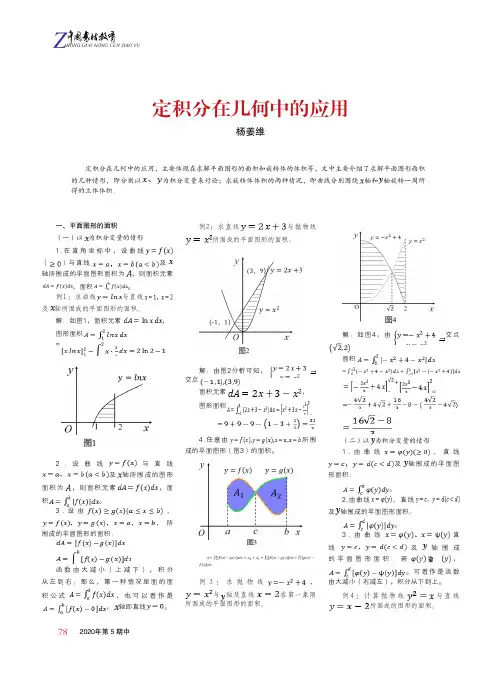
782020年第 5 期中定积分在几何中的应用杨姜维一、平面图形的面积（一）以为积分变量的情形1.在直角坐标中，设曲线（）与直线及轴所围成的平面图形面积为，则面积元素，面积。

例1：求曲线与直线及轴所围成的平面图形的面积。

解：如图1，面积元素，图形面积=2.设曲线与直线及轴所围成的图形面积为，则面积元素，面积。

3.设由，所围成的平面图形的面积：函数由大减小（上减下），积分从左到右；那么，第一种情况里面的面积公式，也可以看作是，轴即直线。

例2：求直线与抛物线所围成的平面图形的面积。

解：由图2分析可知，交点面积元素，图形面积4.任意由所围成的平面图形（图3）的面积。

例3：求抛物线，与轴及直线在第一象限所围成的平面图形的面积。

解：如图4，由交点面积+（二）以为积分变量的情形1.由曲线、直线及轴围成的平面图形面积：。

2.由曲线、直线及轴围成的平面图形面积：。

3.由曲线直线及轴围成的平面图形面积：若，。

可看作是函数由大减小（右减左），积分从下到上。

例4：计算抛物线与直线所围成的图形的面积。

定积分在几何中的应用，主要体现在求解平面图形的面积和旋转体的体积等，文中主要介绍了求解平面图形面积的几种情形，即分别以为积分变量来讨论；求旋转体体积的两种情况，即曲线分别围绕轴和轴旋转一周所得的立体体积。

JIAO HAI TAN HANG／教海探航解：如图5，由交点为方便计算，选取为积分变量，则有4.任意由曲线直线及轴围成的平面图形面积：。

二、旋转体的体积一个平面图形围绕其所在平面上的一条直线旋转一周而成的立体即为旋转体，常见的旋转体有圆柱体、圆锥、圆台、球体等,这些都有对应的体积公式，面对日常生活中所用到的水杯、花瓶等立体物件，求解体积时可考虑以下情况：（一）曲线绕轴旋转的情形由连续曲线与直线及轴所围成的曲边梯形绕轴旋转一周而成的立体，选为积分变量，该旋转体的体积元素，体积为。

（二）曲线绕轴旋转的情形由曲线、直线及轴围成的平面图形绕轴旋转一周所得的立体，选为积分变量，该旋转体的体积元素，体积为。

定积分的简单应用(二)求曲边梯形面积的方法是什么 定积分的几何意义是什么 微积分基本定理是什么引入:我们前面学习了定积分的简单应用一一求面积。

求体积问题也是定积分的一个重要应用。

F 面我们介绍一些简单旋转几何体体积的求法。

1. 简单几何体的体积计算的宽是x X i x i ，i 1,2,L ,n 。

这个“小长条”绕x 轴旋转一周就得到一个厚度是 X i 的小圆片，如图乙所示。

当 x i 很小时，第i 个小圆片近似于底面半径为y i f (x)的小圆柱。

因此，第i 个小圆台的体积V i 近似为V if 2(x)该几何体的体积V 等于所有小圆柱的体积和:这个问题就是积分问题，则有:复习:问题：设由连续曲线y f(x)和直线Xa ， xb 及x 轴围成的平面图形 (如图甲)绕x 轴分析:旋转一周所得旋转体的体积为V ，如何求Vfl J — bX图甲在区间［a, b ］内插入n 1个分点，使b ，把曲线y f (X)( a X b )分割成n 个垂直于x 轴的“小长条”，如图甲所示。

设第i 个“小长条”X i2 2V [ f (X i ) X i f (X 2)2X 2 L f (X n ) X n ]V : f 2(x)dxb 2 af (x)dxS)X o X i X 2 LX n 1X n归纳:设旋转体是由连续曲线y f(x)和直线X a ，X b 及x 轴围成的曲边梯形绕x 轴旋转2. 利用定积分求旋转体的体积分清端点3. 一个以y 轴为中心轴的旋转体的体积若求绕y 轴旋转得到的旋转体的体积，则积分变量变为y ,其公式为V类型一：求简单几何体的体积 例1：给定一个边长为a 的正方形，绕其一边旋转一周，得到一个几何体，求它的体积 思路:由旋转体体积的求法知，先建立平面直角坐标系，写出正方形旋转轴对边的方程，确定 积分上、下限，确定被积函数即可求出体积。

解：以正方形的一个顶点为原点，两边所在的直线为 X, y 轴建立如图所示的平面直角坐标系,如图BC : y a 。

定积分的几何应用定积分的几何应用内容摘要自十七世纪下半叶牛顿和莱布尼茨确定了微积分的基础以来，微积分已经经历了近四百年的发展，微积分不仅在数学领域，在现代科学各个领域都发挥了巨大的作用，微积分的思想更是达到了哲学的高度。

可以预见，微积分在将来的应用会越来越广泛，越来越深入，但微积分由于其思想的复杂性、系统性,给使用者带来了不便，本文就微积分在数学几何领域的应用做了一些总结和创新,得出了在直角坐标系和极坐标系情况下,平面图形的面积、旋转体体积、光滑曲线的弧长和旋转曲面的面积的求解方法，以方便相关领域的人士在工作和学习中参考使用。

【关键词】定积分几何坐标系面积体积弧长The application of definite integral geometryAbstractSince the second half of the seventeenth Century the Newtonian and Leibniz to determine the basis of calculus, calculus has experienced nearly four hundred years of development， not only in the field of mathematics calculus， in modern scientific fields have played an important role， the calculus idea is to achieve a high degree of philosophy。

Can foreknow, calculus in the future will be more widely used, more and more deeply， but due to the complexity of ideas of calculus, system， users have inconvenience， the calculus in mathematics geometry application some summary and innovation， derived in Cartesian coordinate and polar coordinate conditions， planar graph area, the volume of body of rotation， smooth arc length of a curve and a rotating surface area method， so as to facilitate the related people in the working and learning reference。

4.2定积分的简单应用(二)复习：（1） 求曲边梯形面积的方法是什么？（2） 定积分的几何意义是什么？（3） 微积分基本定理是什么？引入：我们前面学习了定积分的简单应用——求面积。

求体积问题也是定积分的一个重要应用。

下面我们介绍一些简单旋转几何体体积的求法。

1. 简单几何体的体积计算问题：设由连续曲线()y f x =和直线x a =，x b =及x 轴围成的平面图形（如图甲）绕x 轴旋转一周所得旋转体的体积为V ，如何求V ？分析：在区间[,]a b 内插入1n -个分点，使0121n n a x x x x x b -=<<<<<=L ，把曲线()y f x =（a x b ≤≤）分割成n 个垂直于x 轴的“小长条”，如图甲所示。

设第i 个“小长条”的宽是1i i i x x x -∆=-，1,2,,i n =L 。

这个“小长条”绕x 轴旋转一周就得到一个厚度是i x ∆的小圆片，如图乙所示。

当i x ∆很小时，第i 个小圆片近似于底面半径为()i i y f x =的小圆柱。

因此，第i 个小圆台的体积i V 近似为2()i i i V f x x π=∆该几何体的体积V 等于所有小圆柱的体积和：2221122[()()()]n n V f x x f x x f x x π≈∆+∆++∆L这个问题就是积分问题，则有：22()()b b a a V f x dx f x dx ππ==⎰⎰归纳：设旋转体是由连续曲线()y f x =和直线x a =，x b =及x 轴围成的曲边梯形绕x 轴旋转而成，则所得到的几何体的体积为2()b a V f x dx π=⎰ 2. 利用定积分求旋转体的体积（1） 找准被旋转的平面图形，它的边界曲线直接决定被积函数（2） 分清端点（3） 确定几何体的构造（4） 利用定积分进行体积计算3. 一个以y 轴为中心轴的旋转体的体积若求绕y 轴旋转得到的旋转体的体积，则积分变量变为y ，其公式为2()b a V g y dy π=⎰类型一：求简单几何体的体积例1：给定一个边长为a 的正方形，绕其一边旋转一周，得到一个几何体，求它的体积 思路：由旋转体体积的求法知，先建立平面直角坐标系，写出正方形旋转轴对边的方程，确定积分上、下限，确定被积函数即可求出体积。