大学固体物理考试题及答案参考培训课件

格式：doc
大小：116.50 KB
文档页数：4

下载文档原格式

/ 4

高校物理专业固体物理学期末考试答案详解

高校物理专业固体物理学期末考试答案详解物理专业固体物理学期末考试答案详解题一：多晶体和单晶体的区别和联系是什么？答：多晶体和单晶体是固体物质的两种不同形态。

多晶体是由许多晶粒组成的，晶粒之间存在取向差异，呈现出无规则的排列和晶格结构。

而单晶体则具有完美的晶格结构，晶粒排列有序。

多晶体和单晶体在结构和性质上存在一些区别和联系。

首先，在结构上，多晶体由许多晶粒组成，晶粒之间存在取向差异，形成无规则的排列和晶格结构；而单晶体由一个晶粒组成，晶粒之间排列有序且具有完美的晶格结构。

同时，在性质上，多晶体的物理性质通常是各晶粒性质的平均值，具有各向同性；而单晶体的物理性质在晶格各个方向上存在明显差异，具有各向异性。

此外，多晶体与单晶体在制备和应用中也存在差异。

多晶体比较容易制备，其制备成本低，适用于大规模生产；而单晶体的制备比较困难，制备成本高，适用于对晶体结构和性质要求较高的领域，如光电子器件和半导体材料等。

总结起来，多晶体和单晶体在结构、性质以及应用方面存在明显的区别。

多晶体具有无规则排列的结构，各向同性的性质，适用于大规模生产；而单晶体具有有序排列的结构，各向异性的性质，适用于对晶体结构和性质要求较高的领域。

题二：介绍一下福克斯效应和拉曼散射现象。

答：福克斯效应（Focke effect）是固体物理中的一种重要现象，描述了光在晶体中传播时的色散性质。

当光波传播到晶体中时，由于晶体中原子的周期性排列，光波的传播速度因晶体的折射率而发生变化，导致光波的传播方向发生偏折的现象。

福克斯效应的具体表现是，在晶体的X射线或电子束射线入射时，会出现衍射条纹，这些衍射条纹的位置和形状与晶体的结构相关。

通过对这些衍射条纹进行分析和测量，可以确定晶体的晶格常数和晶体结构。

另一方面，拉曼散射现象（Raman scattering）是指光波在与物质相互作用时发生频率或波长的变化。

当光波与物质相互作用时，由于光与物质分子之间的相互作用，光波的能量会改变，从而引起光波的频率或波长发生变化。

《固体物理学》基础知识训练题及其参考答案

《固体物理》基础知识训练题及其参考答案说明：本内容是以黄昆原著、韩汝琦改编的《固体物理学》为蓝本，重点训练读者在固体物理方面的基础知识，具体以19次作业的形式展开训练。

第一章作业1：1.固体物理的研究对象有那些？答：（1）固体的结构；（2）组成固体的粒子之间的相互作用与运动规律；（3）固体的性能与用途。

2.晶体和非晶体原子排列各有什么特点？答：晶体中原子排列是周期性的，即晶体中的原子排列具有长程有序性。

非晶体中原子排列没有严格的周期性，即非晶体中的原子排列具有短程有序而长程无序的特性。

3.试说明体心立方晶格，面心立方晶格，六角密排晶格的原子排列各有何特点？试画图说明。

有那些单质晶体分别属于以上三类。

答：体心立方晶格：除了在立方体的每个棱角位置上有1个原子以外，在该立方体的体心位置还有一个原子。

常见的体心立方晶体有：Li，Na，K，Rb，Cs，Fe等。

面心立方晶格：除了在立方体的每个棱角位置上有1个原子以外，在该立方体每个表面的中心还都有1个原子。

常见的面心立方晶体有：Cu, Ag, Au, Al等。

六角密排晶格：以ABAB形式排列，第一层原子单元是在正六边形的每个角上分布1个原子，且在该正六边形的中心还有1个原子；第二层原子单元是由3个原子组成正三边形的角原子，且其中心在第一层原子平面上的投影位置在对应原子集合的最低凹陷处。

常见的六角密排晶体有：Be，Mg，Zn，Cd等。

4.试说明, NaCl，金刚石，CsCl, ZnS晶格的粒子排列规律。

答：NaCl：先将错误!未找到引用源。

两套相同的面心立方晶格，并让它们重合，然后，将一套晶格沿另一套晶格的棱边滑行1/2个棱长，就组成Nacl晶格；金刚石：先将碳原子组成两套相同的面心立方体，并让它们重合，然后将一套晶格沿另一套晶格的空角对角线滑行1/4个对角线的长度，就组成金刚石晶格；Cscl:：先将错误!未找到引用源。

组成两套相同的简单立方，并让它们重合，然后将一套晶格沿另一套晶格的体对角线滑行1/2个体对角线的长度，就组成Cscl晶格。

固体物理40题上课讲义

1. 设晶体中的每个振子的零点振动能.试用德拜模型求晶体的零点振动能.证明:根据量子力学零点能是谐振子所固有的，与温度无关，故T=0K 时振动能0E 就是各振动模零点能之和。

()()()000012mE E g d E ωωωωωω==⎰h 将和()22332s V g v ωωπ=代入积分有402339168m m s V E N v ωωπ==h ，由于098m B D B D k E Nk ωθθ==h 得一股晶体德拜温度为~210K ，可见零点振动能是相当大的，其量值可与温升数百度所需热能相比拟．2. 试画出二维长方格子的第一、第二布里渊区.3. 证明：在磁场中运动的布洛赫电子，在K 空间中,轨迹面积A n 和在r 空间的轨迹面积S n之间的关系A n= (qB hc)2S n()d k d rc qv B q B dt dt⋅=-⨯=--⋅r rr u r h 解：dk qB dr dt c dt∴=⋅h t k qB r ch 两边对积分,即 =22()()n n A r c S k qB∴==h 4. 证明：面心立方晶格的倒格子为体心立方. 解：面心立方晶格的基矢为()()()a a a a j ,b ,c 222k i k i j =+=+=+r r r r r r r r r则面心立方原胞体积3V []4a abc ⋅⨯=r r r =a 2bc V π*⨯=r ru u r 面心立方倒格矢 ()()2384a i k i j a π=⋅+⨯+r r r r ()ai j k π-++r r r 2=()b a i j k π*=-+u u r r r r 2同理：，()ac i j k π*=+-u u r r r r 2a b c***u u r u u r u u r 显然，，为体心立方原胞基矢，因此面心立方晶格倒格子为体心立方 5. 证明：根据倒格子的定义证明简单立方格子体积与其倒格子体积成反比解:设简单立方晶格常数为a ，则基矢为a ,b ,c ,V a ai a j ak ===r r r r r r 3体积=其倒格矢2312b 2a a i V a ππ⨯==u u r u u r u u r r ，3122b 2a a j V a ππ⨯==u u r u r u u r r ，1232b 2a a k V aππ⨯==u r u u ru u r r则倒格子体积()31232[]V b b b Vπ*=⋅⨯=u r u u r u r6. 是否存在与库伦力无关的晶型，为什么？答：不存在与库仑力无关的晶型，因为①共价结合中电子虽不能脱离电负性的原子，但靠近的两个原子各给出一个电子，形成电子共有的形状，位于两原子之间通过库仑力把两个原子结合起来。

固体物理习题解答(课堂PPT)

第一章习题 1.1 何谓布喇菲格子？试画出NaCl晶体的结点所构成的布喇菲格子。
答：所谓布喇菲格子是指晶体由完全相同的原子组成，原子与晶格的格点相重合，而且每个格点周围的情况都一样。（Bravais格子）氯化钠结构：面心立方Na+布氏格子和面心立方Cl-的布氏格子套构而成的复式格子。
1
1.2 为何金刚石结构是复式格子？答：金刚石晶胞位于立方体体内原子和立方体角或面心原子价键的取向各不相同，所以是复式格子
2
2
4
ABC面的密勒指数为 (131) 11
（2）AC晶列的指数
C
cr
uuur uuur uuur AC OC OA
B
r
A
b
[cr
1
(ar
r b
)]
(ar
r b
)
1
r a(i
r j
r 2k
)
ar
2
2
所以AC晶列的晶列指数为 [112]
12
第二章习题
2.1 证明简单六角布喇菲格子的倒格子仍为简单六角布喇菲格子，并给出其倒格子的晶格常数。
设n为一个晶胞中的刚性原子球数，r表示刚性原子球半径， V表示晶胞体积，则致密度为
n 4r3
x 3 V
5
(1) 简单立方
a 任意一个原子球有6个最近邻，若原子以刚性球堆积，则有 a 2r,V a3
晶胞内包含一个原子，所以有： (2) 体心立方
x
4 (a)3
32
a3
6
任意一个原子球有8个最近邻，若原子
以刚性球堆积，则体心原子与处在8个
顶角位置处的原子球相切，因此，对
a
角线长度为 3a 4r r 3 a

大学固体物理试题及答案

·考试时间120 分钟试题Array班级学号姓名一、简答题（共65分）1.名词解释：基元，空间点阵，复式格子，密堆积，负电性。

（10分）2.氯化钠与金刚石是复式格子还是单式格子，各自的基元中包含多少原子？分别是什么原子？（6分）3.在固体物理中为什么要引入“倒空间”的概念？（5分）4.在晶体的物相分析中，为什么使用X光衍射而不使用红外光？（5分）5.共价键的定义和特点是什么？（4分）6.声子有哪些性质？（7分）7.钛酸锶是一种常见的半导体材料，当产生晶格振动时，会形成多少支格波，其中声学支和光学支格波各多少支？（5分）8.晶格振动的Einsten模型在高温和低温下都与实验定律符合吗？为什么？（5分）9.试画出自由电子和近自由电子的D～En关系图，并解释二者产生区别的原因。

（8分）10.费米能级E f的物理意义是什么？在绝缘体中费米能级处在导带、禁带、价带的哪个中？两块晶体的费米能级本来不同，E f1≠E f2，当两块晶体紧密接触后，费米能级如何变化？（10分）二、计算题（共35分）1．铜靶发射λ=0.154nm的X射线入射铝单晶（面心立方结构），如铝（111）面一级布拉格反射角θ=19.2º，试据此计算铝（111）面族的面间距d与铝的晶格常数a。

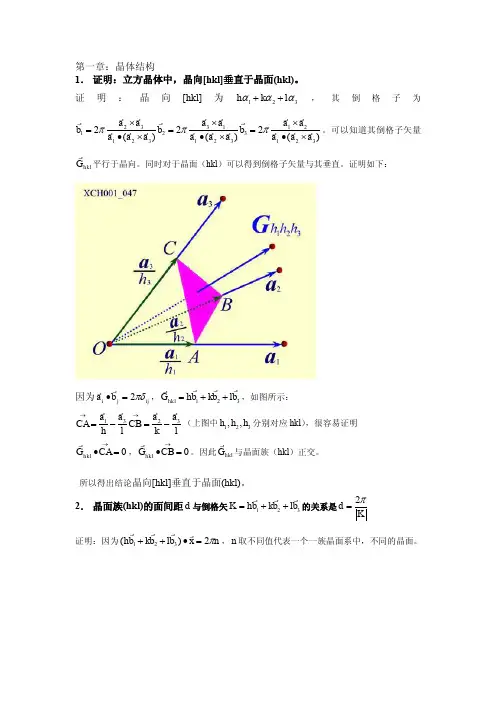
（10分）2．图示为二维正三角形晶格，相邻原子间距为a。

只计入最近邻相互作用，使用紧束缚近似计算其s能带E（k）、带中电子的速度v（k）以及能带极值附近的有效质量m*。

（15分）提示：使用尤拉公式化简3．用Debye模型计算一维单式晶格的热容。

（10分）参考答案一、简答题（共65分）1. （10分）答：基元：组成晶体的最小结构单元。

空间点阵：为了概括晶体结构的周期性，不考虑基元的具体细节，用几何点把基元抽象成为一点，则晶体抽象成为空间点阵。

复式格子：晶体由几种原子组成，但各种原子在晶体中的排列方式都是相同的（均为B格子的排列），可以说每一种原子都形成一套布拉菲子格子，整个晶体可以看成是若干排列完全相同的子格子套构而成。

固体物理习题答案PPT课件

上述八个矢量的垂直平分面，形成了第一布里渊区。
5 解： A2 b c,B 2 c a,C 2 a b
V c
V c
V c
V A (B C ) (2)3( b c )[ c ( a ) ( a b )] V c
A (B C )(A C )B (A B )C
6解：当 KCl 取 ZnS 结构时，晶体总相互作用
能为 utotN(zeRR q2)
已知：N=6.023*1023/mol, ρ=0.326埃，αZnS=1.6381,（见P103) 为NaCl结构时，Zλ=2.05*10-8erg, Z=6 当为ZnS 结构时，Z=4, Zλ=（4/6）*2.05*10-8erg
设ZnS 结构时，其晶格常数与NaCl结构相同，（为原子最近邻距离）
即 a=6.294埃（见P20，图20配位数为6，参见表10，表11， a=2*1.33+1.81=6.2埃），31/2a/4=2.72埃（为原子最近邻距
离）
u to 6 . 0 t 1 2 2 [ 3 0 6 4 2 2 . 0 1 5 8 e 0 0 2 . 3 . 7 2 2 1 . 6 6 2 . ( 3 7 4 . 8 1 8 2 1 8 0 1 0 e 1 5 0 0 ) 3 ] s 1 u . 8 K 5/ m 3 C
第二章习题答案
3解:
（c)衍射先只出现在同时满足以下二个方程的方
向上：（1）acosθ1=nλ,(2) bcosθ2=mλ
(
a,b
为二个方向矢量）
所以在二个锥面的交线上出现衍射极大。当底板
//原子面时，衍射花样为二个锥面的交线与底板
的交点。
（d）反射式低能电子衍射(LEED)中，只有表面层原子参与衍射，故为二维衍射，衍射点的周期大小与晶体表面原子排列方向上周期大小成反比。

(参考资料)固体物理习题带答案

D E ( ) ，其中，表示沿 x ， y ， z 轴的分量，我们选取 x ， y ， z
沿立方晶体的三个立方轴的方向。
显然，一般地讲，如果把电场 E 和晶体同时转动， D 也将做相同转动，我们将以 D' 表示转
动后的矢量。
设 E 沿 y 轴，这时，上面一般表达式将归结为：Dx xyE, Dy yyE, Dz zy E 。现在
偏转一个角度 tg 。（2）当晶体发生体膨胀时，反射线将偏转角度
tg ，为体胀系数
3
解：（1）、布拉格衍射公式为 2d sin ，既然波长改变，则两边同时求导，有
2d cos ，将两式组合，则可得 tg 。
（2）、当晶体发生膨胀时，则为 d 改变，将布拉格衍射公式 2d sin 左右两边同时对 d
考虑把晶体和电场同时绕 y 轴转动 / 2 ，使 z 轴转到 x 轴， x 轴转到 z 轴， D 将做相同
转动，因此
D'x Dz zy E
D'y Dy yyE
D'z Dx xy E 但是，转动是以 E 方向为轴的，所以，实际上电场并未改变，同时，上述转动时立方晶体
的一个对称操作，所以转动前后晶体应没有任何差别，所以电位移矢量实际上应当不变，即
第一章：晶体结构 1．证明：立方晶体中，晶向[hkl]垂直于晶面(hkl)。
证明：晶向 [hkl] 为 h1 k2 l3 ，其倒格子为
b1
2
a1
a2
a3
(a2 a3 )
b2
2
a1
a3 a1 (a2 a3)
b3
2
a1
a1
a2
(a2 a3)
。可以知道其倒格子矢量

固体物理-第一章习题解答参考ppt课件

d 2 r
a
G h h 1 h 2 h 3 2 h 1 h 2 h 3 2 h 1 h 2 h 3 2
上式中等效晶面指数{1,0,0}晶面族、（1,1,1)、(-1,-1,-1)晶面对应的面间距最大，面间距，
d a 3
格点体密度，
1 4
a3
最大面密度，
d.a 43
a 3
4 3a2
1/2属于该等边三角形
2a
(111)
a
2a
(111)
1/6属于该等边三角形
等边三角形面积，
S12a2asin600 3a2
2
2格点面密度，2 4S 3a.21.5 求立方晶系晶面族 h的k l面间距；
cb
a
晶胞基矢 a a i ,b a j,c a k
倒格子基矢 a r2 ir,b r2 r j,c r2 k r
界面方程：
kx
ky
2 a
kx
ky
2 a
2 kx ky a
kx
ky
2 a
与第1布里渊区界面围成的区域为第2布里渊区
.
第3布里渊区：
离原点再次远有４个倒格点 (h12,h20)(,h12,h20), (h10,h22)(,h10,h22)
界面方程：
kx
2
a
,kx
2
a
,
ky
2
a
,ky
2
a
与第1、2布里渊区界面围成区域为第3布里渊区
b
1 2
(b3
b1 )
c
1 2
(b1
b2)
与晶面族(hlk垂)直的倒格矢：
G hkl
h a

固体物理学答案详细版

原胞的体积 = c (a b) = 1 (3i
3j
3k ) (3i
3
j
)
=13.5*
-30
10
3
(m )
2
1.7 六方晶胞的基失为： a
3a
ai j ， b
2
2
3 ai
a j ，c
ck
2
2
求其倒格子基失，并画出此晶格的第一布里渊区
.
答：根据正格矢与倒格矢之间的关系，可得：
正格子的体积 Ω=a·（ b*c ） = 3 a2c 2
相应波矢：
4
,
5a
2 ,0, 2 , 4
5a
5a 5a
由于
4
qa
sin ，代入， m及 q 值
m
2
则得到五个频率依次为（以 rad/sec 为单位）
8.06
× 1013， 4.99 × 1013， 0，4.99 × 1013，8.06 × 1013
3.2 求证由 N 个相同原子组成的一维单原子晶格格波的频率分布函数可以表示为
1.3 二维布拉维点阵只有 5 种，试列举并画图表示之。答：二维布拉维点阵只有五种类型：正方、矩形、六角、有心矩形和斜方。分别如图所示：
正方 a=b a^ b=90°
六方 a=b a^b=120°
矩形 a≠b a^b=90 °
带心矩形 a=b a^b=90 °
平行四边形 a≠ b a^ b≠ 90°
故d
[( h )2
( k )2
(
l
)2]
1 2
a1
a2
a3
1.9 用波长为 0.15405nm 的 X 射线投射到钽的粉末上，得到前面几条衍射谱线的布拉格角

固体物理经典复习题及答案（供参考）

固体物理经典复习题及答案（供参考）⼀、简答题1.理想晶体答：内在结构完全规则的固体是理想晶体，它是由全同的结构单元在空间⽆限重复排列⽽构成的。

2.晶体的解理性答：晶体常具有沿某些确定⽅位的晶⾯劈裂的性质，这称为晶体的解理性。

3.配位数答: 晶体中和某⼀粒⼦最近邻的原⼦数。

4.致密度答：晶胞内原⼦所占的体积和晶胞体积之⽐。

5.空间点阵(布喇菲点阵)答：空间点阵(布喇菲点阵)：晶体的内部结构可以概括为是由⼀些相同的点⼦在空间有规则地做周期性⽆限重复排列，这些点⼦的总体称为空间点阵(布喇菲点阵)，即平移⽮量123d 、d 、h h h d 中123,,n n n 取整数时所对应的点的排列。

空间点阵是晶体结构周期性的数学抽象。

6.基元答：组成晶体的最⼩基本单元，它可以由⼏个原⼦(离⼦)组成，整个晶体可以看成是基元的周期性重复排列⽽构成。

7.格点(结点)答: 空间点阵中的点⼦代表着结构中相同的位置，称为结点。

8.固体物理学原胞答：固体物理学原胞是晶格中的最⼩重复单元，它反映了晶格的周期性。

取⼀结点为顶点，由此点向最近邻的三个结点作三个不共⾯的⽮量，以此三个⽮量为边作的平⾏六⾯体即固体物理学原胞。

固体物理学原胞的结点都处在顶⾓位置上，原胞内部及⾯上都没有结点，每个固体物理学原胞平均含有⼀个结点。

9.结晶学原胞答：使三个基⽮的⽅向尽可能的沿空间对称轴的⽅向，以这样三个基⽮为边作的平⾏六⾯体称为结晶学原胞，结晶学原胞反映了晶体的对称性，它的体积是固体物理学原胞体积的整数倍,V=n ，其中n 是结晶学原胞所包含的结点数, 是固体物理学原胞的体积。

10.布喇菲原胞答：使三个基⽮的⽅向尽可能的沿空间对称轴的⽅向，以这样三个基⽮为边作的平⾏六⾯体称为布喇菲原胞，结晶学原胞反映了晶体的对称性，它的体积是固体物理学原胞体积的整数倍,V=n ,其中n 是结晶学原胞所包含的结点数,是固体物理学原胞的体积11.维格纳-赛兹原胞(W-S 原胞)答：以某⼀阵点为原点，原点与其它阵点连线的中垂⾯(或中垂线) 将空间划分成各个区域。

大学固体物理考试题及答案参考

固体物理训练题之阳早格格创做1.晶体结构中，里心坐圆的配位数为 12 .晶体里里微瞅结构不妨瞅成是由一些相共的面子正在三维空间做周期性无限分集 .固体物理教本胞、结晶教本胞 .格波的能量量子，其能量为 ħωq ，准动量为 ħq .正接归一闭系 .分坐的值，即只可与 Na的整数倍. 7.晶体的面缺陷典型有热缺陷、挖隙本子、纯量本子、色心 .自由电子近似、独力电子近似、无碰碰假设、自由电子费米气体假设 .9.根据爱果斯坦模型，当T→0时，晶格热容量以指数的形式趋于整.10.晶体分离典型有离子分离、共价分离、金属分离、分子分离、氢键分离 . 11.正在千万于整度时，自由电子基态的仄稳能量为 0F 53E . 摩我定容热容为 B m ,23nk C V = .13.依照惯例，里心坐圆本胞的基矢为 ⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=)(2)(2)(2321j i a a k i a a k j a a，体心坐圆本胞基矢为 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=+-=++-=)(2)(2)(2321k j i a a k j i a a k j i a a. 14 .对于晶格常数为a 的简朴坐圆晶体,与正格矢k a j a i a R ˆˆˆ22++=正接的倒格子晶里族的里指数为 122 , 其里间距为 a 32π .15.根据晶胞基矢之间的夹角、少度闭系可将晶体分为 7大晶系，对于应的惟有14种布推伐格子.16.按几许构型分类，晶体缺陷可分为面缺陷、线缺陷、里缺陷、体缺陷、微缺陷 .17. 由共种本子组成的二维稀排晶体，每个本子周围有 6 个迩来邻本子.18.矮温下金属的总摩我定容热容为 3m ,bT T C V +=γ .19. 中子非弹性集射是决定晶格振荡谱最灵验的真验要领.1.固体浮现宏瞅弹性的微瞅真量是什么？本子间存留相互效率力.2.简述倒格子的本量.P29~303. 根据量子表里简述电子对于比热的孝敬，写出表白式，并道明为什么正在下温时不妨不思量电子对于比热的孝敬而正在矮温时必须思量？4.线缺陷对于晶体的本量有何效率？举例道明.P1695.简述基础术语基元、格面、布推菲格子.基元：P9组成晶体的最小基础单元，所有晶体不妨瞅成是基元的周期性沉复排列形成.格面：P9将基元抽象成一个代表面，该代表面位于各基元中等价的位子.布推菲格子：格面正在空间周期性沉复排列所形成的阵列.6.为什么许多金属为稀积结构?问：金属分离中, 受到最小能量本理的拘束，央供本子真与公有电子电子云间的库仑能要尽大概的矮(千万于值尽大概的大).本子真越紧稀，本子真与公有电子电子云靠得便越稀切，库仑能便越矮.所以，许多金属的结构为稀积结构.7.简述爱果斯坦模型，并道明其乐成之处、缺累之处及本果问：爱果斯坦模型：假定所有的本子以相共的频次振荡乐成之处：通过采用符合的爱果斯坦温度值，正在较大温度变更的范畴内，表里估计的截止战真验截止相称佳天切合.且热容量随着温度落矮而趋于整缺累之处：温度非常矮时，热容量按温度的指数形式落矮，而真验测得截止标明：热容量按温度的3次圆落矮本果：是爱果斯坦模型忽略了各格波的频次不共8.金属中公有化电子对于热容孝敬为什么战典范表里值存留较大偏偏好？正在什么情况下应付于电子的热容孝敬给予思量，为什么？由于电子是费米子，按照费米－狄推克分集战泡利不相容本理，果此公有化电子不克不迭局部弥补正在最矮能级上，而是弥补正在能戴中由矮到下准连绝的能级上.正在热激励效率下，惟有费米能附近能级上的电子存留一定跃迁到下能级的机会，进而对于热容有孝敬，而大普遍电子并不介进热激励，那时制成金属中公有化电子对于热容孝敬战典范表里值存留较大偏偏好本果.通过估计创制，电子对于热容量的孝敬战温度的一次圆成正比，而晶格振荡的热容量正在矮温时战温度的三次圆成正比，果此，正在温度趋于整的情况下，电子的热容量是主要圆里，该当给予思量.1.道明自由电子的能级稀度为2123224//)(E m V dE dZ E g ⎪⎭⎫ ⎝⎛==h π.道明：P1902.道明倒格矢332211b h b h b h G h ++=与正格子晶里族（321h h h ）正接. 道明：P303. 道明体心坐圆面阵的倒易面阵是里心坐圆.道明：P31oo o A a A a A a 864321===,,，0012090===γβα,，供： 3.倒易面阵单胞基矢；（2）倒易面阵单胞体积；（3）（210）仄里的里间距.P322. 已知金属钠Na 正在常温常压下的品量稀度3970cm g m /.=ρ，本子量为23，价电子数为1，试推算千万于温度时金属钠Na 的费米能量、费米温度、费米波矢战费米速度.P193×10-24g ，回复力常数为×10-1N/cm.一维单本子链中本子的振荡位移写成如下形式：)cos()(naq t A t x n πω2-=，供：（1）格波的色集闭系；（2）供出由5个本子组成的一维本子晶格的振荡频次.4. 已知金属铜Cu 是里心坐圆晶体，晶格常数a=3.61 10-10m ，每个本子电离时搁出一个自由电子，试推算千万于温度时金属铜的费米能量、费米温度、费米波矢战费米速度.P194V （r ）= r m n r αβ-+表述.若m=2，n=10，而且二本子形成宁静的分子，仄稳时其核间距离为310-10m ，离解能为4eV ，试估计：α战β（10-12J ）P726.一维复式格子的晶格常数为2a，回复力常数为β，大本子品量为M，小本子品量为m，（1）列出本子疏通圆程及解的形式.（2）供特别波的色集闭系w(q).英文文件要领[6]M. D. Segall, Philip J. D. Lindan, M. J. Probert et al.First-principles simulation: ideas, illustrations and the CASTEP code, J.Phys.: Cond. Matt. 2002, 14: 2717–2744。

医科大学精品课件：固体物理作业及答案

久期方程变为
E eikb 0 eikb* E
E2 ( )E ( 2 ) 0
E ( )2 42
2
2
6.5 一维单原子链，原子间距a，总长度为L＝Na
1) 用紧束缚近似方法求出与原子s态能级相对应的能带函数
2) 求出其能态密度函数
的表达式
3) 如每个原子s态中只有一个电子，计算T=0K时的费密能级
6.4 由相同原子组成的一维原子链，每个原胞中有两个原子，
原胞长度为a，原胞内两个原子的相对距离为b ：
(1) 根据紧束缚近似，只计入近邻相互作用，写出原子 s态
相对应的晶体波函数的形式。
(2) 求出相应能带的 E (K) 函数。
黄昆书 4.6 题
解：这是相同原子组成的一维复式格子，设第一套原子格点位置为xn，则第二套原子格点位置为xn+b
解：（1）
势能的平均值
势能的平均值
令
V a2 m2 b2 m 2
96
6
在近自由电子近似模型中，势能函数的第n个傅里叶系数
第一个带隙宽度
Eg1 2V1
8b2
3
m 2
a2
2 3
m 2
第二个带隙宽度
Eg2 2V2
b2
2
m 2
a2
16
2
m 2
6.3 设有二维正方晶格，晶体势场为
U (x, y)
—— s态原子能级相对应的能带函数
—— s原子态波函数具有球对称性
—— 任选取一个格点为原点 —— 最近邻格点有12个
O
12个最邻近格点的位置
O
—— 类似的表示共有12项 —— 归并化简后得到面心立方s态原子能级相对应的能带

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

固体物理练习题
1.晶体结构中，面心立方的配位数为 12 。

2.空间点阵学说认为晶体内部微观结构可以看成是由一些相同的点子在三维空间作周期性无限分布。

3.最常见的两种原胞是固体物理学原胞、结晶学原胞。

4.声子是格波的能量量子，其能量为 ħωq ，准动量为 ħq 。

5.倒格子基矢与正格子基矢满足正交归一关系。

6.玻恩-卡曼边界条件表明描述有限晶体振动状态的波矢只能取分立的值，即只能取 Na
的整数倍。

7.晶体的点缺陷类型有热缺陷、填隙原子、杂质原子、色心。

8.索末菲的量子自由电子气模型的四个基本假设是自由电子近似、独立电子近似、无碰撞假设、自由电子费米气体假设。

9.根据爱因斯坦模型，当T→0时，晶格热容量以指数的形式趋于零。

10.晶体结合类型有离子结合、共价结合、金属结合、分子结合、氢键结合。

11.在绝对零度时，自由电子基态的平均能量为 0F 5
3E 。

12.金属电子的 B m ,23nk C V = 。

13.按照惯例，面心立方原胞的基矢为 ⎪⎪⎪⎩
⎪⎪⎪⎨⎧+=+=+=)(2)(2)
(2321j i a a k i a a k j a a ρρρρρρρ
ρρ ，体心立方原胞基矢为 ⎪⎪⎪⎩
⎪⎪⎪⎨⎧-+=+-=++-=)(2)(2)
(2321k j i a a k j i a a k j i a a ρρρρρρρρρ
ρρρ 。

14 .对晶格常数为a 的简单立方晶体,与正格矢k a j a i
a R ˆˆˆ22++=正交的倒格子晶面族的面
指数为 122 , 其面间距为 a 32π 。

15.根据晶胞基矢之间的夹角、长度关系可将晶体分为 7大晶系，对应的只有14种布拉伐格子。

16.按几何构型分类，晶体缺陷可分为点缺陷、线缺陷、面缺陷、体缺陷、微缺陷。

17. 由同种原子组成的二维密排晶体，每个原子周围有 6 个最近邻原子。

18.低温下金属的总摩尔定容热容为 3m ,bT T C V +=γ 。

19. 中子非弹性散射是确定晶格振动谱最有效的实验方法。

1.固体呈现宏观弹性的微观本质是什么？
原子间存在相互作用力。

2.简述倒格子的性质。

P29~30
3. 根据量子理论简述电子对比热的贡献，写出表达式，并说明为什么在高温时可以不考虑电子对比热的贡献而在低温时必须考虑？
4.线缺陷对晶体的性质有何影响？举例说明。

P169
5.简述基本术语基元、格点、布拉菲格子。

基元：P9组成晶体的最小基本单元，整个晶体可以看成是基元的周期性重复排列构成。

格点：P9将基元抽象成一个代表点，该代表点位于各基元中等价的位置。

布拉菲格子：格点在空间周期性重复排列所构成的阵列。

6.为什么许多金属为密积结构?
答：金属结合中, 受到最小能量原理的约束，要求原子实与共有电子电子云间的库仑能要尽可能的低(绝对值尽可能的大)。

原子实越紧凑，原子实与共有电子电子云靠得就越紧密，库仑能就越低。

所以，许多金属的结构为密积结构。

7.简述爱因斯坦模型，并说明其成功之处、不足之处及原因
答：爱因斯坦模型：假定所有的原子以相同的频率振动
成功之处：通过选取合适的爱因斯坦温度值，在较大温度变化的范围内，理论计算的结果和实验结果相当好地符合。

且热容量随着温度降低而趋于零
不足之处：温度非常低时，热容量按温度的指数形式降低，而实验测得结果表明：热容量按温度的3次方降低
原因：是爱因斯坦模型忽略了各格波的频率差别
8.金属中共有化电子对热容贡献为什么和经典理论值存在较大偏差？在什么情况下应对电子的热容贡献予以考虑，为什么？
由于电子是费米子，遵循费米－狄拉克分布和泡利不相容原理，因此共有化电子不能全部填充在最低能级上，而是填充在能带中由低到高准连续的能级上。

在热激发作用下，只有费米能附近能级上的电子存在一定跃迁到高能级的机会，从而对热容有贡献，而大多数电子并没有参与热激发，这时造成金属中共有化电子对热容贡献和经典理论值存在较大偏差原因。

通过计算发现，电子对热容量的贡献和温度的一次方成正比，而晶格振动的热容量在低温时和温度的三次方成正比，因此，在温度趋于零的情况下，电子的热容量是主要方面，应该予以考虑。

1.证明自由电子的能级密度为2123224//)(E m V dE dZ E g ⎪⎭
⎫ ⎝⎛==h π。

证明：P190 2.证明倒格矢332211b h b h b h G h ++=与正格子晶面族（321h h h ）正交。

证明：P30
3. 证明体心立方点阵的倒易点阵是面心立方。

证明：P31
1.一个单胞的尺寸为o
o o A a A a A a 864321===,,，0012090===γβα,，求：
（1）倒易点阵单胞基矢；（2）倒易点阵单胞体积；（3）（210）平面的面间距。

P32
2. 已知金属钠Na 在常温常压下的质量密度3970cm g m /.=ρ，原子量为23，价电子数为1，试推算绝对温度时金属钠Na 的费米能量、费米温度、费米波矢和费米速度。

P193
3.设原子质量为m=8.35×10-24g ，恢复力常数为β=1.5×10-1N/cm 。

一维单原子链中原子的振动位
移写成如下形式：)cos()(naq t A t x n πω2-=，求：
（1）格波的色散关系；
（2）求出由5个原子组成的一维原子晶格的振动频率。

4. 已知金属铜Cu 是面心立方晶体，晶格常数a=3.61 ⨯10-10m ，每个原子电离时放出一个自由电子，试推算绝对温度时金属铜的费米能量、费米温度、费米波矢和费米速度。

P194
5.设两原子间的相互作用能可由
V （r ）= r m n r αβ
-+
表述。

若m=2，n=10，而且两原子构成稳定的分子，平衡时其核间距离为3 ⨯10-10m ，离解能为4eV ，试计算：α和β（1eV=1.60⨯10-12J ）
P72
6. 一维复式格子的晶格常数为2a ，恢复力常数为β，大原子质量为M ，小原子质量为m ，（1）列出原子运动方程及解的形式。

（2）求出格波的色散关系ω(q )。

英文文献格式[6]M. D. Segall, Philip J. D. Lindan, M. J. Probert et al. First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Cond. Matt . 2002, 14: 2717–2744。