李宏毅-B站机器学习视频课件Ensemble (v6)

李宏毅机器学习课程——Lifelonglearning学习笔记概述lifelong learning⾮常直观，意思是机器不能前边学后边忘。

常见的⽅法是对前边的task中学习出来的参数加⼀个保护系数，在后⾯的任务中，训练参数时，对保护系数⼤的参数很难训练，⽽保护系数⼩的参数则容易⼀些。

下⾯的图⾮常直观，颜⾊的深浅代表loss的⼤⼩，颜⾊越深loss越⼩。

在task1中θ2的变化对loss的变化⾮常敏感，⽽θ1则不敏感，所以在task2中尽量只通过改变θ1来减⼩loss，⽽不要改变θ2。

在lifelong learning中，loss的计算公式如下：L′(θ)=L(θ)+λΣi b i(θi−θb i)2其中b i就是对θ的保护系数，θi表⽰本次task中需要学习的参数，θb i是从之前的task中学习到的参数。

不同的⽅法差异就在于b i的计算。

这⾥将会结合Coding整理⼀下遇到的三个⽅法。

Coding这部分针对HW14，介绍了EWC，MAS，SCP三种⽅法，这⾥讲解⼀下具体的代码实现，并定性地分析⼀下这些⽅法是如何把哪些重要的参数保护起来。

EWCEWC中不同的保护系数f i使⽤如下的⽅法计算得到：F=[∇log(p(y n|x n,θ∗A))∇log(p(y n|x n,θ∗A))T]F的对⾓线的各个数就是各个θ的保护系数。

p(y n|x n,θ∗A)指的就是模型在给点之前 task 的 data x n以及给定训练完 task A (原来)存下来的模型参数θ∗A得到y n(x n对应的 label ) 的后验概率。

其实对参数θi，它的保护系数就是向量log(p(y n|x n,θ∗A))对θ1的偏导数∂log(p(y n|x n,θ∗A))∂θ1与⾃⾝的内积。

当对这个参数敏感时，这个偏导数会变⼤，当预测结果正确率⾼时，p(y n|x n)也会⾼，最终都会使的保护系数变⼤。

某⼀个参数⽐较敏感，这个参数下正确率⾼时，这个参数就会被很好地保护起来。

李宏毅2021春机器学习课程笔记——⽣成对抗模型模型本⽂作为⾃⼰学习李宏毅⽼师2021春机器学习课程所做笔记，记录⾃⼰⾝为⼊门阶段⼩⽩的学习理解，如果错漏、建议，还请各位博友不吝指教，感谢！！概率⽣成模型概率⽣成模型（Probabilistic Generative Model）简称⽣成模型，指⼀系列⽤于随机⽣成可观测数据的模型。

假设在⼀个连续或离散的⾼维空间\(\mathcal{X}\)中，存在⼀个随机向量\(X\)服从⼀个未知的数据分布\(p_r(x), x \in\mathcal{X}\)。

⽣成模型根据⼀些可观测的样本\(x^{(1)},x^{(2)}, \cdots ,x^{(N)}\)来学习⼀个参数化的模型\(p_\theta(x)\)来近似未知分布\(p_r(x)\)，并可以⽤这个模型来⽣成⼀些样本，使得⽣成的样本和真实的样本尽可能地相似。

⽣成模型的两个基本功能：概率密度估计和⽣成样本（即采样）。

隐式密度模型在⽣成模型的⽣成样本功能中，如果只是希望⼀个模型能⽣成符合数据分布\(p_r(x)\)的样本，可以不显⽰的估计出数据分布的密度函数。

假设在低维空间\(\mathcal{Z}\)中有⼀个简单容易采样的分布\(p(z)\)，\(p(z)\)通常为标准多元正态分布\(\mathcal{N}(0,I)\)，我们⽤神经⽹络构建⼀个映射函数\(G : \mathcal{Z} \rightarrow \mathcal{X}\)，称为⽣成⽹络。

利⽤神经⽹络强⼤的拟合能⼒，使得\(G(z)\)服从数据分布\(p_r(x)\)。

这种模型就称为隐式密度模型（Implicit Density Model）。

隐式密度模型⽣成样本的过程如下图所⽰：⽣成对抗⽹络⽣成对抗⽹络（Generative Adversarial Networks，GAN）是⼀种隐式密度模型，包括判别⽹络（Discriminator Network）和⽣成⽹络（Generator Network）两个部分，通过对抗训练的⽅式来使得⽣成⽹络产⽣的样本服从真实数据分布。

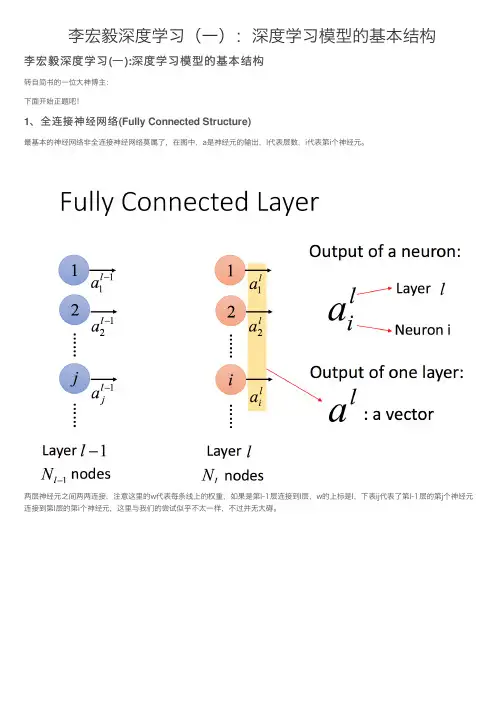
李宏毅深度学习（⼀）：深度学习模型的基本结构李宏毅深度学习(⼀):深度学习模型的基本结构转⾃简书的⼀位⼤神博主：下⾯开始正题吧！1、全连接神经⽹络(Fully Connected Structure)最基本的神经⽹络⾮全连接神经⽹络莫属了，在图中，a是神经元的输出，l代表层数，i代表第i个神经元。

两层神经元之间两两连接，注意这⾥的w代表每条线上的权重，如果是第l-1层连接到l层，w的上标是l，下表ij代表了第l-1层的第j个神经元连接到第l层的第i个神经元，这⾥与我们的尝试似乎不太⼀样，不过并⽆⼤碍。

所以两层之间的连接矩阵可以写为如下的形式：每⼀个神经元都有⼀个偏置项：这个值记为z，即该神经元的输⼊。

如果写成矩阵形式如下图：针对输⼊z，我们经过⼀个激活函数得到输出a：常见的激活函数有：这⾥介绍三个：sigmoidSigmoid 是常⽤的⾮线性的激活函数，它的数学形式如下：特别的，如果是⾮常⼤的负数，那么输出就是0；如果是⾮常⼤的正数，输出就是1，如下图所⽰：.sigmoid 函数曾经被使⽤的很多，不过近年来，⽤它的⼈越来越少了。

主要是因为它的⼀些 缺点：**Sigmoids saturate and kill gradients. **（saturate 这个词怎么翻译？饱和？）sigmoid 有⼀个⾮常致命的缺点，当输⼊⾮常⼤或者⾮常⼩的时候（saturation），这些神经元的梯度是接近于0的，从图中可以看出梯度的趋势。

所以，你需要尤其注意参数的初始值来尽量避免saturation的情况。

如果你的初始值很⼤的话，⼤部分神经元可能都会处在saturation的状态⽽把gradient kill掉，这会导致⽹络变的很难学习。

Sigmoid 的 output 不是0均值. 这是不可取的，因为这会导致后⼀层的神经元将得到上⼀层输出的⾮0均值的信号作为输⼊。

产⽣的⼀个结果就是：如果数据进⼊神经元的时候是正的(e.g. x>0 elementwise in f=wTx+b)，那么 w 计算出的梯度也会始终都是正的。