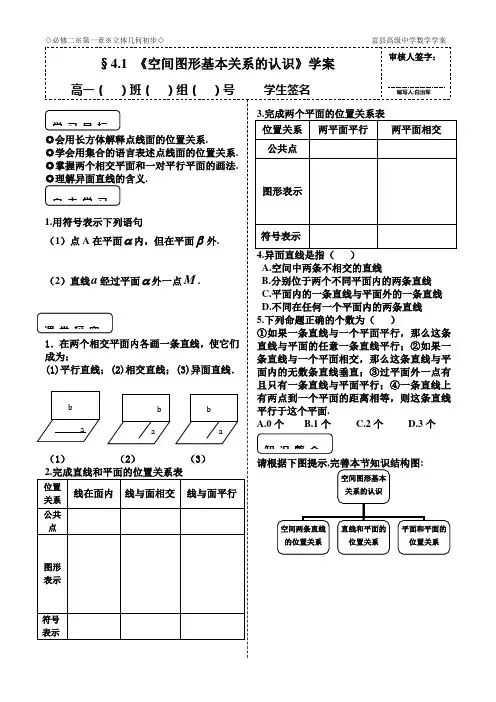
空间图形基本关系的认识1
- 格式:ppt
- 大小:76.00 KB
- 文档页数:10



第二部分空间与图形(一)线与角本单元是小学数学总复习的第二部分“空间与图形”领域的知识,通过系统的整理与复习,使学生巩固和加深理解小学阶段所学的“空间与图形”的知识,进一步沟通知识之间的联系,发展学生的空间观念,提高解决实际问题的能力,为进一步学习和发展奠定基础。
这部分的内容主要包括;图形的认识、图形的测量、图形与变换、图形与位置四部分。
其中第一部分又包括:线与角、平面图形、立体图形,第二部分包括长度、面积和体积。
教学目标:1.引导学生系统整理学过的图形,沟通图形之间的联系,形成知识网络。
2.结合具体的物体或图形,引导学生从不同的角度研究立体图形,沟通立体图形与平面图形之间的联系,发展学生的空间观念。
3.能运用所学的的知识和技能解决日常生活中的简单问题,体会数学与生活的密切联系。
4.引导学生交流整理知识的方法。
对这部分内容进行复习时应重点指导学生再次感知图形特征,以此强化、扩展和沟通图形之间的联系,再通过一定的练习进行巩固。
根据内容特点和小学生的年龄特征,教材在安排图形的认识的复习时分了两大部分。
第一部分是“系统整理,沟通联系”,主要是引导学生系统整理学过的图形,沟通图形之间的联系,形成有机联系的“空间与图形”的知识网络;第二部分是“把握特征、练习深化”,主要是从“线与角”、“平面图形”、“立体图形”三个方面引导学生在头脑中再现各种图形的特征,进行整理与内化,并通过一些典型的练习,进一步巩固和深化学生对图形的认识。
对于线与角的教学,教材给了四个方面的问题,引导学生对线与角的知识进行回顾与整理。
第一个问题是引导学生复习“直线、线段、和射线”的有关知识。
教学时可以先让学生画一画,然后进行交流;也可以让学生列表进行比较。
第二个问题是。
引导学生复习垂直与平行。
教学时可以先让学生画一画,并说说判断直线垂直或平行的基本方法。
第三个问题是引导学生比较角的大小,复习角的测量等知识。
教学时,要让学生说说测量角的方法,并让每个学生用量角器量角。



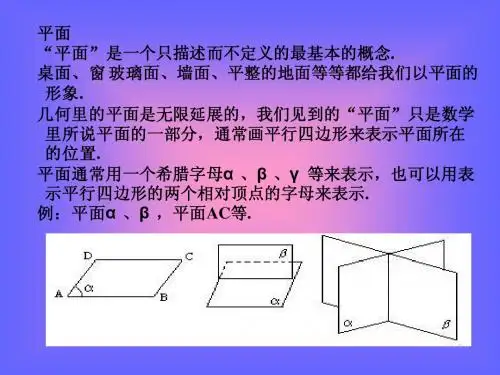
空间几何的相交和平行关系空间几何是研究三维形体的相对位置和关系的学科,而其中最基本和重要的概念之一就是相交和平行关系。
在本文中,我们将探讨这两个概念的含义以及它们在空间几何中的应用。
1. 相交关系相交关系是指两个或多个图形在空间中有交集的情况。
具体来说,当两个或多个图形的部分或全部相互穿越时,我们可以说它们相交。
在空间几何中,常见的相交关系有以下几种:1) 点与直线的相交:当一条直线与一个点相交,即该点在直线上,我们可以说点与直线相交。
2) 点与平面的相交:当一个点与一个平面相交,即该点在平面上,我们可以说点与平面相交。
3) 直线与直线的相交:当两条直线在空间中有一个公共点时,我们可以说它们相交。
4) 直线与平面的相交:当一条直线与一个平面有一个公共点时,我们可以说它们相交。
5) 平面与平面的相交:当两个平面在空间中有一条直线作为它们的交集时,我们可以说它们相交。
相交关系在几何推理和几何证明中起着重要的作用。
通过分析图形的相交关系,我们可以得出很多有用的结论和性质,进而解决问题。
2. 平行关系平行关系是指两个或多个图形在空间中没有交集的情况。
具体来说,当两个或多个图形的部分或全部没有交点时,我们可以说它们平行。
在空间几何中,常见的平行关系有以下几种:1) 直线与直线的平行:当两条直线在空间中没有交点,且它们的方向相同或重合时,我们可以说它们平行。
2) 直线与平面的平行:当一条直线与一个平面没有交点,且这条直线在这个平面上的任意一条平行线上时,我们可以说它们平行。
3) 平面与平面的平行:当两个平面没有交集,且它们的法向量平行时,我们可以说它们平行。
平行关系在几何推理和几何证明中也是非常重要的。
通过研究图形的平行性质,我们可以得出很多结论和性质,从而解决各种实际问题。
总结:空间几何中的相交和平行关系是非常基础且重要的概念。
相交关系指的是两个或多个图形在空间中有交集,而平行关系指的是两个或多个图形在空间中没有交集。



小学数学认识空间几何和立体形的基本概念数学作为一门抽象的学科,对于小学生来说可能会有些难以理解。
但是通过引入实物和具体的例子,可以帮助学生更好地理解和掌握数学知识。
在小学数学中,认识空间几何和立体形是很重要的一部分。
本文将介绍小学数学中认识空间几何和立体形的基本概念,并通过实例来加深理解。
1. 认识空间几何空间几何是研究空间中的点、线、面以及它们之间的相互关系的学科。
在小学数学中,初步认识空间几何可以从认识基本几何图形开始,如点、线、面等。
一、点点是空间中没有长度、宽度和高度的几何图形。
它只有位置,用字母来表示,如A、B。
点可以用铅笔在纸上标出来,也可以用线段来表示。
二、线段线段由两个端点确定,具有有限的长度。
线段用两个字母表示,如AB。
线段的长度可以通过实际测量得到。
三、面面是由无限条线段组成的平坦的二维几何图形。
用外形类似的实物,如纸片、墙面等可以形象化地帮助学生理解。
面可以用大写字母表示,如P。
2. 认识立体形立体形是由线、面等组成的有一定厚度、体积的几何图形。
在小学数学中,主要会学习球体、立方体、长方体的基本概念。
一、球体球体是由无数条长度相等的曲线围成,且中心到任意一点的距离都相等,形状像圆球。
球体可以通过实物,如足球、篮球等来进行形象认识。
二、立方体立方体是有六个面,每个面都是一个正方形,且相邻两个面是平行的。
立方体可以通过实物,如魔方、盒子等来进行形象认识。
三、长方体长方体是有六个面,其中相对的两个面是相等的长方形。
长方体可以通过实物,如书本、钢笔盒等来进行形象认识。
通过认识和学习这些立体形的基本概念,可以帮助小学生了解和区分不同的几何图形,培养他们的空间认知能力。
3. 实例分析为了更好地理解空间几何和立体形的基本概念,我们以一个实例进行分析。
小明有一本长方体的书,书的宽度是10厘米,高度是20厘米,长度是30厘米。
请问这本书的体积是多少?解答:根据题目所给的信息,我们可以通过计算长方体的体积来得出答案。