第三章理想光学模型(8)
- 格式:ppt
- 大小:564.50 KB
- 文档页数:30








![[数学]第3章 理想光学系统](https://uimg.taocdn.com/6cc9e79b960590c69fc3760f.webp)

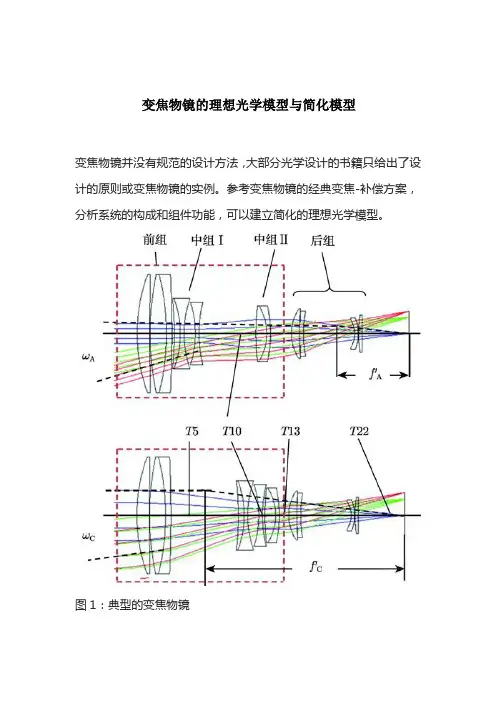
变焦物镜的理想光学模型与简化模型变焦物镜并没有规范的设计方法,大部分光学设计的书籍只给出了设计的原则或变焦物镜的实例。
参考变焦物镜的经典变焦-补偿方案,分析系统的构成和组件功能,可以建立简化的理想光学模型。
图1:典型的变焦物镜在图1中,变焦组的前组和两个中组构成望远系统(afocal系统)。
在短焦端Config A,中组I紧贴前组,构成负光焦度的复合前组,中组II为正光焦度的后组,构成倒置的伽利略望远镜。
在长焦端Config C,中组I紧贴中组II,构成负光焦度的复合中组,前组为正光焦度,构成正置的伽利略望远镜,角放大率为ρ,加上后组,系统焦距为f`C。
显然f`C>f`A,比率f`C/f`A,就是变焦比ZR。
. 1.变焦物镜的理想光学模型图2:变焦物镜的理想光学模型如果把前组、中组与后组都近似看作薄透镜,就可以得到理想光学模型,如图2所示。
其中第1、第2和第3透镜构成afocal系统,即伽利略望远镜。
(1)在短焦端Config A假定透镜1与透镜2是密接透镜组,则有通常有望远镜的反向角放大率假定光阑在透镜3和透镜4之间,且这两个透镜的间隔很小,略去主光线通过两个透镜的角度变化,则在前后组间隔内主光线与光轴的夹角为它也是像空间的视场角。
反远摄物镜的前后组的间隔表达式为设轴上大光线入射高为h A,后组的入射高为h`,则有系统焦距为(2)在长焦端Config C望远镜的反向角放大率设轴上大光线入射高为h C,则有系统焦距为由此可以得到变焦比:在理想光学模型中,短焦端和长焦端相当于倒置和正置的伽利略望远镜,系统正是通过“内调焦”实现变焦。
. 2.变焦物镜的简化模型作为设计初值,假定如下:我们得到一组解,各参数的关系为在短焦端 Config A:上式中,-h pA是前组透镜外径的一半。
在长焦端 Config C:上式中,-h pC是前组透镜外径的一半。
系统参数如下:(a)变焦区间:(b)角视场变化范围:(c)望远镜前后组间隔:(d)系统总长:(e)像空间角视场:(f)后组入射高:. 3.变焦物镜的计算过程一个变焦物镜的设计,一般预先给出了像高y`,相对孔径1/F和变焦比ZR,由计算得到ρ与r。
应用光学第3章 理想光学系统3.1 理想光学系统的概念及性质3.2 理想光学系统的基点和基面、焦距3.3 理想光学系统的成像3.4 理想光学系统的组合3.5 透镜3.1 理想光学系统的概念及性质3.1.1 理想光学系统的概念3.1.2 理想光学系统的性质实际的光学系统要求用一定宽度的光束、对一定大小的范围成像。
在估计其成像质量时,需利用理想光学系统成像的概念。
如果光学系统对任意大的范围,以任意大的光束成像都是完善的,这样的光学系统便定义为理想光学系统。
1)物空间的每一点对应于像空间中的一点,且只有唯一的一点与之相对应,这两个对应点称为物像空间的共轭点。
2)物空间中的每一条直线对应于像空间中的一条直线,且只有唯一的一条直线与之相对应,这两条对应直线称为物像空间的共轭线。
3)物空间的任意一点位于直线上,那么其在像空间内的共轭点也必位于该直线的共轭线上。
4)物空间中的任一平面对应于像空间中的一个平面,且只有唯一的一个平面与之相对应,这两个对应平面称为物像空间的共轭面。
3.2 理想光学系统的基点和基面、焦距3.2.1 焦点、焦平面3.2.2 主点和主平面3.2.3 焦距3.2.4 节点和节平面图3-1 基点和基面图3-2 无限远轴外点和物方焦平面上点发出的光束a)无限远轴外点发出的光束 b)物方焦平面上点发出的光束如图3-1所示,延长入射光线A1E1和出射光线GkF′得交点Q′,同样延长光线A′kEk及物方的共轭光线G1F交于Q点。
根据光路的可逆性,物方光线FG1入射于光学系统后,其像方光线必沿E kA′k出射,物方光线A1E1入射于光学系统后,其像方光线必沿GkF′方向出射,显然Q和Q′是一对共轭点,分别过Q和Q′作垂直于光轴的平面QH、Q′H′交光轴于H点和H′点,此两平面同样也是共轭的。
由图可知QH=Q′H′=h,故其放大率β=+1,称这对放大率为+1的共轭面为主平面,QH称为物方主平面(前主面或第一主面),Q′H′称为像方主平面(后主面或第二主面)。