当前位置：文档之家 › 点的速度合成定理

点的速度合成定理

  • 格式：ppt
  • 大小：489.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

牵连运动为定轴转动时点的加速度合成定理

牵连运动为定轴转动时点的加速度合成定理

理论力学
aa ae ar aC
即当牵连运动为转动时，动点的绝对加速度等于牵连加速度、相对 加速度与科氏加速度的矢量和。这就是牵连运动为转动时点的加速 度合成定理。
设动点沿直杆 OA 运动，杆 OA 又以角速度 绕O 轴匀速转动。
将动坐标系固结在杆上。在瞬时 t ，动点在 OA杆的M 位置， 它的相对速度、牵连速度分别为 vr 和 ve ，经时间间隔 t后， 杆OA 转动 角，动点运动到 OA 杆的M 点处，这时动点的相 对速度、牵连速度分别为 vr 和 ve ，如图6-10（a）所示。
又由图6-10（c）可知 ve ve1 ve2 （c）
式中，ve1 表示由于牵连速度方向变化而引起的牵连速度增量；ve2 表示由于存在相对运动使牵连速度大小变化而引起的牵连速度增量。
将式（b）、式（c）一起代入式（a），可得
aa
lim vr1 t0 t
lim vr2 t0 t
lim ve1 t0 t
将式（e）、式（f）和式（6-11）一并代入式（d），于是牵连
运动为转动时点的加速度合成定理得到证明，
即式（d）可写成
aa ae ar aC
所得结论也适用于一般情况。科氏加速度的表达式为
aC 2e vr
根据矢量积运算法则，aC 的大小为
aC 2evr sin
式中， 是矢量e与vr 的夹角；
lim ve2 t0 t
lim ve ve t0 t
lim OM OM
t0
t
vr
其方向也垂直于 vr，并与 转向一致。
由于这两项附加加速度的大小相同，方向一致，所以，两项合
并成一项，用 aC 表示，它的大小为
aC 2vr
它的方向与 vr 垂直，并与 转向一致。这项加速度称为科氏加速度。

8-2 速度合成定理

8-2 速度合成定理

ve──t瞬时动点的牵连速度 动为任何运动的情况。
2
速度合成定理的应用
曲柄滑杆机构
•应用速度合成定理时，动点和动系的选择原则 (1)动点相对动系必须有相对运动； (2)动点的相对运动轨迹要简单清晰。 •解题方法 (1)几何法 (2)解析法
3
例1：凸轮顶杆机构
相对轨迹
绝对轨迹
v
vr
φ
va
ve
φ
牵连轨迹
uuuuur uuuuur uuuuuur
MM
uuuuur
'
MMuu1uuur
M1M
'
uuuuuur
lim MM ' lim MM1 lim M1M '
t0 t
t0 t
t0 t
uuuuuur
uuuuuur
lim M1M ' lim MM 2
t0 t
t0 t
由速度定义可知
uuuuur
uuuuur
uuuuuur
lim
t 0
MM t
'
va
lim
t 0
MM1 t
ve
lim MM 2 t0 t
vr
上一节 下一节 返回上级1 菜单
Ⅰ(t)
vr
va
ve
o o
ⅡΔ o
va ve vr
称为速度合成定理 速度合成定理的几何意义：
速度平行四边形
va──t瞬时动点的绝对速度
速度合成定理适用于绝
vr──t瞬时动点的相对速度 对运动、相对运动和牵连运
Q O1A l2 r2 2r sin 1/ 2 ve r / 2
Q ve 1g2r

点的速度合成定理

点的速度合成定理

va v r y
ve ＊
x
x
va
ve
tan30 2 3e
3
vr
2va
4 3e
3
vABva
2 3e
3
■ 点的速度合成定理 ★ 应用举例
1、选择动点、动系、定系
要选择合适的动点、动系。
解 2、运动分析
题
绝对运动与相对运动都是指点的运动，它可能作
步
直线运动或曲线运动。 牵连运动则是指参考体的运动即刚体的运动，它
O x
牵连点：M′（脚牵印连）点（：甲？板上）
va vr ve 三者关系？
★ 速度合成定理
z y
z o
x
刚性金属丝
y
O
小环
x
动点：小环（沿金属丝滑动）
定系（ oxy）z ：固定于地面
动系（ oxyz ）：固连于刚性金属丝
★ 速度合成定理
☆
z
zz
动 系 的
o z y x o x y o
oy
x
运
骤 可能作平动、转动或其它较复杂的运动。
3 、速度分析及其求解
牵连速度：某瞬时动系上与动点相重合的那一点
（称为牵连点）相对于定系的速度；
由 va vrve 作平行四边形，其对角线为v a ；
va vr ve 满足“6-4=2”方可求两个未知量。
■ 点的速度合成定理 ★ 讨论与思考
例 1中
动点：滑块A 动系：固连于O1B杆 绝对运动：绕O点的圆周运动 相对运动：沿滑杆的直线运动
牵连运动：绕O1轴的定轴转动
y
B
x
●A
O1
动点： O1B杆上的A点 动系：固连于OA杆

大连理工大学理论力学第13课

大连理工大学理论力学第13课

l 2 r 22 ve ve r 1 2 2 O1 A l2 r2 l r
已 知 ： O A 常 数 , O A r , O O 1 l , O A 水 平 。 求 ： 1。 rl r 2 r 2 vr ve 1 2 2 2 2 2 2 l r l r l r
重点：
1.点的复合运动的基本概念。 2.明确一个动点、两个坐标系和三种运动。
3.点的速度合成定理、加速度合成定理及其应用。
难点：
1.正确判定动点的相对运动，能正确地在动系上观察动点 的运动。 2.牵连点的概念，以及牵连速度、牵连加速度和 科氏加速度的判断与计算。
3.动点、动系的选择。
点的速度合成定理：
vr2 aax ' ' 2 v cos r r
aa aax ' aay '
2
2
方向由其方向余弦确定
例7-11 刨床的急回机构如图所示。当曲柄OA 以匀
3.加速度
n aa aet aen
例7-11
a r aC
大小 2 r ? 12 O1 A ? 21vr √ √ √ √ 方向 √ 沿 x 轴投影
n ax t e t e
2 2 2 2 rl l r a rl （l r ) 2 1 3 2 2 2 2 2 2 2 2 O1 A l r l r l r
例7-10
已知：vr ,ω, φ, CO=r 求：aa 解：1. 动点：气体微团C， 动系 ： Ox’y’ 2. 绝对运动：未知
相对运动：曲线运动（AB）
牵连运动：定轴转动（O轴)

第七章 第二节 点的速度合成定理

第七章 第二节 点的速度合成定理

ve
(3) 作速度平行四边形。 (注意:va为平行四边形的对角线) (4) 利用几何关系解出未知量。
Hale Waihona Puke va vrD Aw
O l
ve va cos 45 2u / 2
j
B u
ve 2u / 2 u w OA 2l 2l bu D点速度 v D bw 2l
2 2 vr ve va 2ve va cosq
3 3R
例(P152例7-4)已知定滑轮半径为R，以等角速度w绕轴O顺时针 方向转动，重物M铅垂下落。试求图示瞬时M相对于滑轮的相 对速度。 解(1)动点：M， w 动系：滑轮。 O (2)分析三种运动和三种速度。 q (3)作速度平行四边形。 (4)利用几何关系解出未知量。
例7-5 (P153例7-5 ) 杆BCD以匀速v1向右运动，杆OA以匀角速度w 绕O转动，当q=45º 时，OM为l。试求该瞬时销钉M的绝对速度。 x 解(1)动点：M， D (2)先取BCD为动系 A ve2 (3)运动、速度分析 有 va = ve1 + vr1 (4)再取OA为动系 ve1 M (5)运动、速度分析 有 va = ve2 + vr2 动点M速度唯一，得
vr1
ve1 + vr1 = ve2 + vr2
vr2
w
向x 轴投影 ve1 sinq vr 1 cosq ve 2 B ve1sinq - ve 2 vr 1 v1 2lw cosq 2 2 2 va ve1 vr 1 2 v1 - 2 2 v1l w + 2 l 2w 2
tan j v r 1 v 1 2 lw 1 ve1 v1 2 lw v1

7-2-3 点的速度合成定理习题(2)

7-2-3 点的速度合成定理习题(2)

B
α1
ω1
θ
O1
R C
ω
O
动点、动系的选取
方案1：
A
动点：摇杆O1A上的点B来自动系：固定在偏心轮 C上
B
方案2：
动点：偏心轮 C上的点B 动系：固定在摇杆O1A上
θ
O1
R C
ω
O
两种方案的绝对运动和相对运动运动轨迹
方案1: (动点: 摇杆O1A上的点B ； 动系: 固定在偏心轮 C上)
绝对运动轨迹： 以O1为圆心，O1B 为半径的圆弧
ve1 = 0.6 3(m / s)
vr1 = −0.8(m / s)
ve2 = 0.2 3(m / s) vr2 = −0.4(m / s)
vay
ve1
A
大小 vax = −ve1 sin 300 = −0.3 3(m / s)
ω2
vay = ve1 cos300 + vr1 = 0.1(m / s)
ve2 = ω2 ⋅OM = ω2 ⋅b / cos 300 = 0.2 3(m / s)
3）速度合成定理：
va = ve2 + vr 2
大小 ×
√
×
方向 ×
√
√
y2′ M
O ω1
b
A x2′
B ω2 vr 2
300
ve2
C
va = ve1 + vr1
大小 ×
√×
方向 ×
√√
ve1
B
A ω2
M
vr 2
va = ve2 + vr 2
大小 × √ ×
O
ω1
300
vr1

《点的速度合成》课件

《点的速度合成》课件

04
点的速度合成定理的实 例分析
实例一：刚体平动的速度合成
总结词
刚体平动速度合成是点速度合成的最简单情 况，主要涉及平移运动的速度合成。
详细描述
刚体平动是指刚体在平面上的直线运动，其 上任意一点的速度合成遵循平行四边形法则 。设刚体平动速度为V，刚体上任意一点P 的速度为v，则v的方向与V相同，大小为V 减去P点相对于刚体质心的线速度。
对未来研究的展望
深入研究点的速度合成定理的数 学基础
为了更好地理解和应用点的速度合成定理，需要深入研 究其数学基础，包括向量运算、线性代数等方面的知识 。
探索更多应用场景
随着科学技术的发展，点的速度合成定理的应用场景将 不断拓展。未来可以探索其在机器人学、虚拟现实等领 域的应用，为相关领域的发展提供理论支持。
定理在其他领域的应用
航空航天领域
点的速度合成定理在航空航天领域有广泛应用。例如，飞机和火箭在飞行过程中需要考 虑到风速、气流等因素对它们运动状态的影响，这些都可以通过应用点的速度合成定理
来计算。
车辆工程
车辆工程师在设计车辆时需要考虑轮胎与地面之间的摩擦力、风阻等因素对车辆运动状 态的影响。通过应用点的速度合成定理，可以更准确地模拟和预测车辆的运动状态。
THANKS FOR WATCHING
感谢您的观看
刚体质心的距离。
实例三：刚体定点运动的速度合成
要点一
总结词
要点二
详细描述
刚体定点运动是指刚体上某一点绕定点转动的情况，其上 任意一点的速度合成需要考虑到定点和转动轴的影响。
在刚体定点运动中，任意一点P的速度合成包括绕定点转动 的线速度和由于刚体转动而产生的向心加速度。线速度的 大小等于刚体角速度乘以点P到定点的距离，向心加速度的 大小等于刚体角速度的平方乘以点P到定点的距离。同时， 由于刚体的转动，点P还会产生一个与转动轴垂直的离心加 速度，其大小等于角速度的平方乘以点P到转动轴的距离。

点的加速度合成定理

点的加速度合成定理
2
rM rO'
O
r'
z'
k' j'
y'
drM y + x O xi i y j z k =r j z k dt = ve v r va =
i'
x'
O' y
d 2 rM aa = 2 = r O x i y j z k dt + xi yj zk y ) i k + 2( x j z y ) i k ae ar 2( x j z
8.3 点的加速度合成定理 va ve vr
即：动点在某一瞬时的绝对速度等于它在该瞬时的牵连速度 与相对速度的矢量和。这就是点的速度合成定理。
aa ae a r ？
8.3 点的加速度合成定理
一、当牵连运动是定轴转动时，动系
i, j, k
(2) 动点相对于动参考系的运动，称为相对运动；
(3) 动参考系相对于定参考系的运动，称为牵连运动。
8.1 相对运动· 牵连运动· 绝对运动
定参考系
牵连运动
动参考系
动点
一点、二系、三运动
8.1 相对运动· 牵连运动· 绝对运动
(1) 动点相对于定参考系的速度、加速度和轨迹， 称为动点的绝对速度va、绝对加速度aa和绝对轨迹。 (2) 动点相对于动参考系的速度、加速度和轨迹， 称为动点的相对速度vr、相对加速度ar和相对轨迹 。 由于动参考系的运动是刚体的运动而不是一个点 的运动，所以除非动参考系作平动，否则其上各点的 运动都不完全相同。因为动参考系与动点直接相关的 是动参考系上与动点相重合的那一点 ( 牵连点 ) ，因此 定义：

《理论力学》第三章点的合成运动(三)

《理论力学》第三章点的合成运动(三)
求：摆杆O1B角速度1
解：A-动点，O1B-动系，基座-静系。
绝对速度va = r
相对速度vr = ? 牵连速度ve = ?
由速度合成定理 va= vr+ ve
sin
r
r 2 l
2
,ve
va
sin

r 2
r2 l2
又ve
O1
A1
,1

ve O1 A

1 r 2 l2
A
cR

O

u
x

r 2
r 2 l2

r
r
2
2
l
2
（
）
[例] 圆盘凸轮机构
已知：OC＝e , R 3e , （匀角速度）
图示瞬时, OCCA 且 O,A,B三点共线。 求：从动杆AB的速度。
解：动点A，动系-圆盘， 静系-基座。 绝对速度 va = ? 待求，方向//AB 相对速度 vr = ? 未知，方向CA
例图示平面机构，已知：OA=r，0为常数，BC=DE， BD=CE=L，求：图示位置，杆BD的角速度和角加速度。
解： 动点：A点(OA杆)
动系：BC杆
va ve vr
D
E
大小： 方向：
？？
B
600 A
vr
300 C
0 O
根据速度合成定理 va ve vr va
ve
做出速度平行四边形, 如图示
E
投至y轴：
0 O aa
aa ae
si
n (
300 ae n aa aen ) sin
sin 60 0
sin 30 0

8.3点的速度合成定理

8.3点的速度合成定理

8.3点的速度合成定理
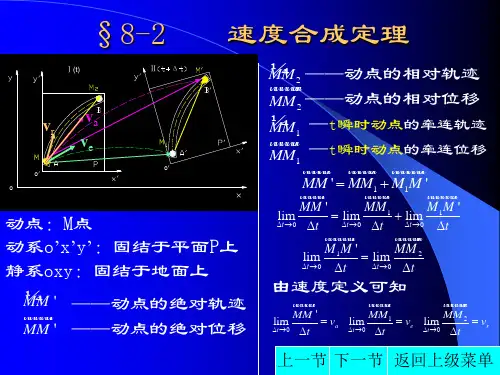
点的速度合成定理是一个基本的运动学定理，它建立了动点的绝对速度、相对速度和牵连速度之间的关系。

具体来说，在任一瞬时，动点的绝对速度等于其牵连速度与相对速度的矢量和。

这个定理可以用数学表达式表示为：绝对速度 = 相对速度 + 牵连速度。

在实际应用中，动点、动系的选择是求解合成运动问题的关键。

通过选择适当的动点和动系，可以利用速度平行四边形来求解未知的速度分量。

此外，加速度合成定理也是解决这类问题的重要工具。

需要注意的是，当牵连运动是平移时，点的加速度合成定理为：绝对加速度 = 牵连加速度 + 相对加速度。

此外，当牵连运动是定轴转动时，点的加速度合成定理为：瞬时绝对加速度 = 瞬时牵引加速度 + 相对加速度 + 科氏加速度（科氏加速度是由于牵连运动中的角速度产生的加速度）。

综上所述，点的速度合成定理和加速度合成定理是解决合成运动问题的重要工具，通过适当选择动点和动系，结合速度平行四边形和加速度合成定理，可以求解未知的速度和加速度分量。

点的加速度合成定理

点的加速度合成定理
静系取在地面上动系取在杆上则?1rlve??21?rlae???222rlve??2222?rlae??oo????1m2m1ev?1ea?2ev?2ea?重点要弄清楚牵连点的概念82点的速度合成定理rmrormmojkiyzxxyzomo????rrrxyz?????????rijkmm??rrddrxyzt?????????rvijk动系上与动点重合的点牵连点在定系中的矢径记为rm在图示瞬时有相对速度vr是动点相对于动参考系的速度因此ijk是常矢量
4. 必须选某点为动点，而动系要取两次； 5. 根据题意，必须取两次动点和动系；
6. 两个不相关的动点，可根据题意来确定；
第十二页，编辑于星期日：十三点 十分。
8.3 点的加速度合成定理 va ve vr
即：动点在某一瞬时的绝对速度等于它在该瞬时的牵连速度
与相对速度的矢量和。这就是点的速度合成定理。
度 转动，圆盘半径为r，绕
轴以o角 速度 转动。求圆盘边
ve2
缘 和 点的M牵1 连速M 2度和加速 M 2
ae2 ve1
ae1
o
度。
o M1
解：静系取在地面上，动系取在
杆上，则
ve1 (l r) ae1 (l r) 2
ve2 l 2 r 2
重点要弄清楚牵 连点的概念
ae2 l 2 r 2 2
第七页，编辑于星期日：十三点 十分。
8.2 点的速度合成定理
rM rO r r = xi yj zk
z M(M')
动系上与动点重合的点(牵连点)在定 系中的矢径记为rM' ，在图示瞬时有
rM rM
动点的相对速度vr为
vr
=
dr dt
=
xi

点的速度合成定理绝对速度动点对于...

点的速度合成定理绝对速度动点对于...

=
R2 R1
a
2
an
=
R2ω 2
=
⎛ R2 ⎜⎜
⎝
2ah R1
⎞ ⎟⎟ ⎠
=
2R2 R12
ah
2
2
a=
aτ2 + an2 =
⎛ ⎜⎜ ⎝
R2 R1
a
⎞ ⎟⎟ ⎠
+
⎛ ⎜⎜ ⎝
2R2 12
ah
⎞ ⎟⎟ ⎠
=
R2a R12
R12 + 4h2
3.3 点的合成运动 点的合成运动的概念
如图示，桥式起 重机在起吊重物 时，假设横梁不 动，起重机小车 沿横梁作水平运 动，同时，小车 上悬挂的重物向 上运动。
2
站在地面上观察重物时，重物的运动轨迹为曲线。 而站在小车上 观察重物时，重物的运动却是垂直向上 的。
由此可得结论：相对于某一参考系的运动可看成相 对于其他参考系的几个简单运动组合而成，这种运动 称为合成运动。
绝对运动、相对运动及牵连运动
点的速度合成定理
(a
n C
)2
=
(aτA )2
+
(a
n A
)
2
= (αl) 2 + (ω 2l) 2
= l α2 +ω4
【例】轮Ⅰ和轮Ⅱ固连，半径分别为R1和R2，在轮Ⅰ上 绕有不可伸长的细绳，绳端挂重物A，如图所示。若重物 自静止以匀加速度a下降，带动轮Ⅰ和轮Ⅱ转动。求当重 物下降了h高度时，轮Ⅱ边缘上B2点的速度和加速度的大 小。
求：C点的运动 轨迹、 速度和加速度
例 题1
解：板运动过程中， 其上任意直线始终平 行于它的初始位置。 因此，板作平移。

点的速度合成定理的适用条件是

点的速度合成定理的适用条件是

点的速度合成定理的适用条件是什么？点的速度合成定理是物理学中的一个重要定理，它描述了两个向量之间的合成关系。

具体来说，它可以用来计算一个点在平面上或空间中的速度向量。

在本文中，我们将详细介绍点的速度合成定理以及其适用条件。

一、定义点的速度合成定理是指，在平面或空间中，一个物体在不同方向上的速度可以通过将这些方向上的速度向量相加得到。

换句话说，如果一个物体同时沿着x轴和y轴移动，那么它的总速度可以表示为x轴和y 轴上分别对应速度向量之和。

二、公式点的速度合成定理可以用以下公式表示：V = √(Vx² + Vy²)其中V表示总速度，Vx表示沿着x轴方向的速度，Vy表示沿着y轴方向的速度。

三、适用条件点的速度合成定理适用于以下情况：1. 物体在平面或空间内运动。

2. 物体在不同方向上有不同的运动速率。

3. 物体在任意时间内都保持匀变速直线运动。

4. 物体在任意时间内都保持匀变加速直线运动，并且加速度在各个方向上都保持不变。

5. 物体在任意时间内都保持匀速圆周运动，并且圆心位于某一轴上。

四、应用举例1. 平面运动假设一个物体在平面内以速度V1沿着x轴运动，以速度V2沿着y轴运动。

则根据点的速度合成定理，该物体的总速度可以表示为：V = √(V1² + V2²)2. 空间运动假设一个物体在空间内以速度V1沿着x轴运动，以速度V2沿着y轴运动，以速度V3沿着z轴运动。

则根据点的速度合成定理，该物体的总速度可以表示为：V = √(V1² + V2² + V3²)总之，点的速度合成定理是物理学中非常重要的一个定理，在平面和空间中都有广泛的应用。

只有了解其适用条件，才能正确地应用它来解决问题。

点的速度合成定理

点的速度合成定理
凸轮上动点 A 相对于杆 AB 的运动不明显，不能 清楚地判定相对运动轨迹，自然无法判定相对速度的方向和 大小，不能求解。
本例的两种解法说明，如何适当选择动点和动系是用合成法分 析问题的关键。在应用速度合成定理时，有下列两点请读者注 意。 （1）分析由主动件和从动件构成的机构时，一般取它们的连接 点为动点，但动点固连于主动件或从动件应由相对轨迹能否容 易被观察而判定。 （2）如果构件 A上的点相对构件 B 运动轨迹易知，则动系固连 于 B ；反之，如构件 B上的点相对构件 A 运动轨迹易知，动系 应固连于构件 A 。当然动点和动系决不应在同一构件上，否则 就没有了相对运动，合成法也就毫无意义了。
在速度合成定理的矢量式中，只有绝对速度 和相对速度的大小两个未知量，可求得
va ve tan v0 tan 30 0.577v0
图6-5（a）
取凸轮上的 A 点为动点，把动系固结在杆 AB 上， 如图6-5（b）所示。
由于凸轮做平动，动点的绝对运动是水平直 线运动，速度的大小和方向均是已知的。牵 连运动为杆 AB 沿铅垂方向的平动，杆上 A 点为牵连点，牵连速度方向已知，大小未知。
度的大小为
vr va2 ve2 u12 u22
vr 的方向如图6-4所示，其中tan u1 /u2 。
例6-2
如图6-5（a）所示，半径为 的半圆形靠模凸轮以等速 v0沿水 平轨道向左运动，带动受有约束的杆 AB 沿铅垂方向平动。求
当 30 时，杆AB 的速度。 解
杆 AB做平动，且在 A 点与已知运动的凸轮相 接触，故只需求杆上 A点的速度。
速度方向已知，大小为 r ；相对运动为
动点沿 O1B 方向的直线运动，相对速度方向 已知但大小未知；牵连运动为杆 O1B 的定
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
MM ′ lim t = va t →0
MM 1 lim t = ve t →0
M 1M ′ MM 2 = lim lim t t →0 t = vr t →0
9.2
点 的 速 度 合
于是可得： 于是可得：
M2
B
va ve
M′
B′
va = ve + vr
vr
M
M1
A
A′
即：动点在某一瞬时的绝对速度等于它在该 瞬时的牵连速度与相对速度的矢量和。 瞬时的牵连速度与相对速度的矢量和。这就 是点的速度合成定理。 点的速度合成定理。
例2
9.2
点 的 速 度 合
x′ ω ve = 180 × 0.083 = 15m / s = 54km / s R
vA 45 × 103 ω= = = 0.083rad / s y′ R 3600 ×150 O
vA
vB A vr 2 B
ve
vr 2 = v + v = 80.72km / h
2 B 2 e
例2
9.2
点 的 速 度 合
如图车A沿半径为150m vA 的圆弧道路以匀速vA = 45km h 行驶， vB O 车B沿直线道路以匀速 vB = 60km h B A R 行驶 ，两车相距30m，求：（1） A车相对B车的速度；（2）B车相 对A车的速度。 解：（1）以车A为动点，静系取在地面上， 动系取在车B上。动点的速度合成矢量图如图。 由图可得：
下面研究点的绝对速度、 下面研究点的绝对速度、牵连速度和相对速 9.2 度的关系。 点 度的关系。 B M ′ B′ M2 如图，由图中矢量关系可得： 如图，由图中矢量关系可得： 的
速 度 合
MM ′ = MM 1 + M 1M ′
将上式两端同除 t ，并
M
M1
A
A′
令 t → 0 ，取极限，得 取极限， MM ′ MM 1 M 1M ′ lim t = lim t + lim t t →0 t →0 t →0 由速度的定义： 由速度的定义：
于是有：
v2 D v 1 α B
va = ve1 + vr1
（1）
v1 A
ve1
va
2
α
v2
M vr 1
D v 1 B
以小环M为动点，静系取在地面上，动系取在 CD杆上，动点的速度合成矢量图如图。 于是有：a
va = ve 2 + ve1
（2）
v1 A v2
ve 2
ve 54 sin α 2 = = = 0.669 vr 2 80.72
α 2 = 42
强调牵连运动为转动
例3
9.2
点 的 速 度 合
水平直杆AB在半径为r的固定圆环上以匀 速 u 竖直下落，如图。试求套在该直杆和圆环交 点处的小环M的速度。 解：以小环M为动点，静系 取在地面上，动系取在AB杆上， 动点的速度合成矢量图如图。 A
于是可得： 即：
1 2 vM = va = v + v = v + 2 (v1 cos α v2 ) sin α 1 2 = v12 + v2 2v1v2 cos α sin α
2 e1 2 r1 2 1
本节结束
例2
9.2
点 的 速 度 合
2 2 2 vr1 = v A + ve2 = v A + vB = 75km / h O v A 45 sin α1 = = = 0 .6 vr1 75 R
ve
vA
A
vr y ′
vB B
x′
α1 = 36.9
（2）以车B为动点，静系取在地面上，动系取 在车A上。动点的速度合成矢量图如图。
v2 D v 1 vr 2 α B
M
v2 ve1 va D v1 ve 2 αvr 2 B M vr 1
ξ
C
比较（1）、（2）式，可得：
ve1 + vr1 = ve 2 + vr 2
建立如图的投影轴，将上 式投影到投影轴上，得：
v1 A v2
C
例6
9.2
点 的 速 度 合
ve1 cos α + vr1 sin α = ve 2 1 1 vr 1 = (ve1 cos α ve 2 ) = (v1 cos α v2 ) sin α sin α
A
B
ωvr o
va v e
α
C R
解：以凸轮圆心C为动点，静系取在地面上， 动系取在顶杆上，动点的速度合成矢量图如图。 由图可得：
2 ve = va cos α = eω cos 45 = eω 2
例6
v 两直杆分别以 v1 、 2 的速度 v 9.2 1 点 沿垂直于杆的方向平动，其交 A M 的 角为α ，求套在两直杆上的小 v2 C 速 环M的速度。 解：以小环M为动点，静系取在地面上，动系 度 取在AB杆上，动点的速度合成矢量图如图。 v
vr
O
va
A
ve
va = ve ctg = v0 ctg vr = vetg = v0tg
牵连点：轮上的 点 牵连点：轮上的A点
例5
9.2
点 的 速 度 合
图示平底顶杆凸轮机构，顶 杆AB可沿导轨上下平动，偏心凸 轮以等角速度ω 绕O轴转动，O轴 位于顶杆的轴线上，工作时顶杆 的平底始终接触凸轮表面，设凸 轮半径为R，偏心距OC=e ，OC 与水平线的夹角为α ，试求当 = 45 α 时，顶杆AB的速度。
u
由图可得：
O
M vr B
rv
e
va
u
ve u = va = sin sin
例4
9.2
点 的 速
如图半径为R的半圆形凸轮以匀速 v0 沿水平轨 道运动，带动顶杆AB沿铅垂滑槽滑动，求在图示位 置时，杆AB的速度。
B
度 合
解：以杆端A为动点，静系 取在地面上，动系取在凸轮上， 动点的速度合成矢量图如图。 v0 由图可得：