- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1.1 图
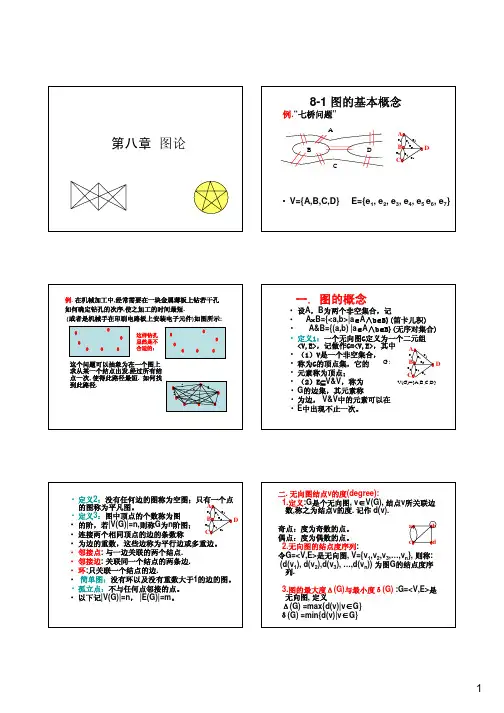
• 著名的柯尼斯堡七桥问题。在柯尼斯堡的普莱格 尔河上有七座桥将河中的岛及岛与河岸联结起来, 如下图所示,A、B、C,D表示陆地。
• 问题是要从这四块陆地中任何一块开始,通过每 一座桥正好一次,再回到起点。
8.1.1 图
• 欧拉在1736年解决了这个问题,他用抽象分析 法将这个问题化为第一个图论问题:即把每一块 陆地用一个点来代替,将每一座桥用联接相应的 两个点的一条线来代替,从而相当于得到一个 「图」。欧拉证明了这个问题没有解,并且推广 了这个问题,给出了对於一个给定的图可以某种 方式走遍的判定法则。这项工作使欧拉成为图论 〔及拓扑学〕的创始人。
• 解: 图中的结点集为:V={v1,v2,v3,v4} 边集为E={l1,l2,l3} l1={v1,v2}, l2={v1,v4}, l3={v2,v3}, -------无序结点对 这个图可以用G=<V,E>表示
8.1.2 图的基本概念
• 例8.2 有4个程序p1,p2,p3,p4, 它们间有一些调用 关系:p1调用p2;p2能调用p3;p1能调用p4, 试将 此事实用图的方式表示.
• (a)(b)同构,(c)(d)同构
8.1.4 图中结点的次数
• 定义8.3
• 在有向图中, 以结点v为起点的边的条数称为v的 引出次数, 记以deg(v); 以v为终点的边的条数叫v 的引入次数, 记以deg(v); v的引入次数与引出次 数之和称为v的次数或全次数, 记为deg(v).
• 在无向图中, 结点v的次数或全次数是与v相关联 的边的条数, 也用deg(v)表示.
• 在计算机科学中,图论在形式语言、数据 结构、分布式系统、操作系统及数据库研 究中均有很重要的应用.
• 本篇结构
– 第八章 介绍图论一般原理 – 第九章 介绍一些常用的图如平面图、两步图
以及树等
第八章 图论原理
• 本章主要介绍图论的基本原理,包括图论 中的基本概念、基本方法以及图论的矩阵 计算等内容.
• 一个图与其补图是互补的 • 一个图的补图的补图还是自己
8.1.3 图的同构
• 定义8.2
设有图G=<V,E>与G’=<V’,E’>, 如果它们的结点 间存在一一对应关系, 而且这种对应关系也反映 在表示边的结点对中(如果是有向边, 则对应的结 点对还保持相同的顺序), 则称此两图是同构的.
8.1.3 图的同构
• 如果有V’⊂V, E⊂E’, 则称G’是G的真子图. • 如果有V’=V, E⊆E’, 则称G’是G的生成子图.
8.1.2 图的基本概念
• (n,m)图: 一个具有n个结点、m条边所组成的图
• 零图: 由一些孤立点组成的图, 即(n,0)图
• 平凡图: 由一个孤立结点组成的图, 即(1,0)图
8.1.2 图的基本概念
• 有序结点对所对应的边称为有向边,无序结点对 所对应的边称为无向边
• 有向图:图中的所有边均为有向边 • 无向图:图中的所有边均为无向边
8.1.2 图的基本概念
• 有向边lk={vi,vj}中, vi称为lk的起点, vj称为lk的终点 • 不管lk是有向还是无向, 均称lk与vi和vj相关联, 而vi
和vj称为邻接的. • 若干条边关联于同一个结点, 则这些边称为邻接
的.
8.1.2 图的基本概念
• 一条边若与两个相同的结点相关联, 则称为环, 即 lk={vi,vi}
• 不与任何结点相邻的结点称为孤立点
8.1.2 图的基本概念
• 图G=<V,E>与G’=<V’,E’>间如果有V’⊆V, E⊆E’, 则称G’是G的子图.
• 解: 图中的结点集为:V={p1,p2,p3,p4} 边集为E={c1,c2,c3} c1={p1,p2}, c2={p2,p3}, c3={p1,p4}, -----有序结点对 这个图可以用G=<V,E>表示
8.1.2 图的基本概念
• 一般,用带有箭头的边表示有序结点对,而用不 带箭头的边表示无序结点对.
图论
图论
• 图论是用图的方法研究客观世界的一门科 学.
• 用“结点”表示事物, 用“边”表示事物 之间联系, 而由结点与边所构成的图表示 所研究的客观对象.
• 图论研究图的逻辑结构与性质,是研究图 的抽象性质的一种数学.
图论
• 图论在语言学、逻辑学、物理学、化学、 电气工程、计算机网络、计算机科学及数 学的其他分支中有广泛应用.
• 任一图的所有结点的次数之和必为偶数, 且必为 图中边数的两倍, 因为每条边必与两个结点相关 联.
8.1.4 图中结点的次数
• 题(8.1) 设V={u,v,w,x,y}, 画出图G=<V,E>:
1) E = {(u,v),(u,x),(v,w),(v,y)(x,y)}
2) E = {(u,v),(v,w),(w,x),(w,y)(x,y)}
8.1.2 图的基本概念
• 定义 8.1
图G是由非空结点集合V={v1,v2,…,vn}以及边集合 E={l1,l2,…,lm}所组成, 其中每条边可用一个节点 对表示, 亦即
li = (vi1,vi2), i = 1,2,…,m 这样一个图G可用G = <V,E>表示
8.1.2 图的基本概念
• 例8.1 有4个城市: v1,v2,v3,v4, 其中v1与v2间; v1与 v4间; v2与v3间有直达长话线路相连, 将此试试用 图的方式表示
• 完全图: 一个(n,m)图G如果其n个结点(n≥2)中的 每一个均与其中n-1个结点邻接, 可记为Kn. m=n(n-1)/2
8.1.2 图的基本概念
8.1.2 图的基本概念
• 补图: 设有一图G=(V,E), 对图G’=(V,E’), 如果有 G=(V,EE')是完全图且E∩E’= Ø 则称G’是G的补图.
8.1.1 图
• 起源:
• 历史上图论曾经被好多位数学家各自独立地建立 过。关于图论的文字记载最早出现在欧拉1736 年的论着中,他所考虑的原始问题有很强的实际 背景。
Leonhard Euler , (1707—1783),瑞士数学 家、力学家、天文学家、 物理学家,图论的创始人, 变分法的奠基人,复变函 数论的先驱者,理论流体 力学的创始人。