温度与水中声速对照表
- 格式:xls
- 大小:76.00 KB
- 文档页数:6

声速与温度计算公式
声速与温度之间的关系可以通过以下公式进行近似计算:
v = 331.4 + 0.6 * T
其中,v 表示声速(单位为米/秒),T 表示温度(单位为摄氏度)。
这是一个常用的近似公式,适用于常温(20-30摄氏度)下的空气中声速的计算。
公式中的常数值331.4是在标准大气压(101.325千帕)和相对湿度为0%的条件下所得到的近似值。
需要注意的是,该公式只适用于空气中声速的近似计算。
对于其他介质(如水、金属等),其声速与温度的关系可能有所不同。
另外,此公式是在常温下的近似计算,随着温度的变化,声速的计算需要考虑更为复杂的影响因素。
对于更精确的声速计算,需要考虑温度、湿度、介质的性质等因素,并采用相应的计算方法或查阅相应的数据表。

水的响度随温度变化的规律
池塘水温是随气温的变化而变化,但由于水本身的热学特性,使池塘水温的变化有其独特性,主要表现在池塘水温变化幅度要比气温小得多。
一昼夜平均温度,水温要高于气温,白天平均水温一般低于平均气温,而晚上则高于气温。
水温最高时间是14至15时,比高气温时间晚1至2时,清晨水温最低。
白天水表层温度一般高于水下层温度,两者之差可达2至3℃或更高,晚上则相反,形成水的热成层。
鱼的体温与水温,鱼类是变温动物,其体温随水温变化而变化,一般比其所在水温高1至2℃。
鱼不能像人类那样通过新陈代谢活动来保持自身温度的恒定,而只能与水温保持相对的稳定(鱼的最佳生理代谢温度是15至25℃)。
低于4℃或高于35℃时,鱼儿就会产生生理不适,甚至停止进食或者死亡。
所以,水温决定着鱼儿的生死存亡。
但鱼儿能自主的主动寻找适合它生理活动的水温区域,因此,适度的水深有宜于鱼类生存和生长。

声速测定实验声波是一种在弹性媒质中传播的机械波。
声波在媒质中传播时,声速,声衰减等诸多参量都和媒质的特性与状态有关,通过测量这些声学量可以探知媒质的特性及状态变化。
例如,通过测量声速可求出固体的弹性模量;气体、液体的比重、成分等参量。
在自由空间同一媒质中,声速一般与频率无关,例如在空气中,频率从20赫兹变化到8万赫兹,声速变化不到万分之二。
由于超声波长短,易于定向发射,不会造成听觉污染等优点,我们通过测量超声波的速度来确定声速。
超声波在医学诊断,无损检测,测距等方面都有广泛应用。
实验目的1.了解超声换能器的工作原理和功能2.学习不同方法测定声速的原理和技术3.熟悉测量仪和示波器的调节使用4.测定声波在空气及水中的传播速度实验原理1.压电陶瓷换能器压电材料受到与极化方向一致的应力F时,在极化方向上会产生一定的电场E,它们满足线性关系:E=g·F反之,当在压电材料的极化方向上加电压E时,材料的伸缩形变S与电压E也呈线性关系:S=a·E系数g、a称为压电常数,它与材料性质有关。
本实验采用压电陶瓷超声换能器,将实验仪输出的正弦振荡电信号转换成超声振动。
压电陶瓷片是换能器的工作物质,它是用多晶体结构的压电材料(如钛酸钡,锆钛酸铅等)在一定的温度下经极化处理制成的。
在压电陶瓷片的前后表面粘贴上两块金属,组成的夹心型振子,就构成了换能器。
由于振子是以纵向长度的伸缩,直接带动头部金属作同样纵向长度伸缩,这样所发射的声波,方向性强,平面性好。
每一只换能器都有其固有的谐振频率,换能器只有在其谐振频率上,才能有效的发射(或接收)。
本实验中使用一个换能器作为发射器,另一个作为接收器,二换能器的表面互相平行,且谐振频率匹配。
2.声速的测量方法声速的测试方法可以分为两类。
第一类方法是直接根据速度关系式:v=S/t测出传播距离S和所需时间t后即可算出声速,该法称为“时差法”,这是工程应用中常用的方法。
第二类方法是利用波长频率关系式:v=f·λ测量出频率f和波长λ来计算出声速,测量波长时又可用“共振干涉法”或“相位比较法”,本实验可用上述三种方法测量气体、液体以及固体中的声速。
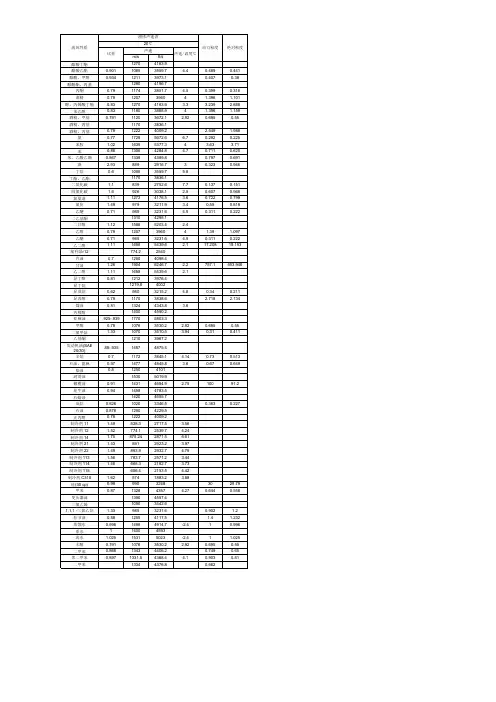

Del Grosso声速公式是用于计算水中声速的一个经验公式,也被广泛用于其他液体中的声速计算。
该公式由Del Grosso在1963年提出,经过大量实验数据验证和修正,被认为是目前最为准确的声速计算公式之一。
Del Grosso声速公式的计算公式为:1. 在20摄氏度以下的温度范围内,声速的计算公式为:c = 1402.85 + 5.0385 * T - 5.xxxe-2 * T^2 + 3.3432e-4 * T^3 -1.xxxe-6 * T^4 + 3.1464 * (S - 35) + 4.9067e-4 * (S - 35)^2其中, c 为声速(单位:m/s),T为水的温度(单位:摄氏度),S为盐度。
2. 在20摄氏度及以上的温度范围内,声速的计算公式为:c = 1449.2 + 4.591 * T - 5.304e-2 * T^2 + 2.374e-4 * T^3 -1.373e-6 * T^4 + 1.345 * (S - 35) + 1.63e-2 * (S - 35)^2需要注意的是,这两个公式的单位都是国际标准单位。
Del Grosso声速公式的优点有以下几点:1. 准确性高:通过大量的实验数据验证和修正,Del Grosso声速公式被认为在水中声速计算中具有较高的准确性。
2. 适用范围广:Del Grosso声速公式不仅适用于水,还可以在一定范围内适用于其他液体中的声速计算,具有较强的通用性。
Del Grosso声速公式的局限性也是存在的:1. 适用范围有限:虽然Del Grosso声速公式在20摄氏度以下和20摄氏度以上的温度范围内都有相应的计算公式,但是在特殊温度下(如冰冷或高温)的准确性和适用范围有所限制。
2. 需要盐度数据:在海洋声速计算中,需要准确的盐度数据作为输入,而这对于某些实际应用而言可能不太方便。
Del Grosso声速公式作为一种经验公式,具有较高的准确性和适用性,被广泛应用于水中声速计算和海洋声学领域。


公式也是有一定的误差的,具体如下已知超声波速度与温度的关系如下:式中:r —气体定压热容与定容热容的比值,对空气为1.40,R —气体普适常量,8.314kg·mol-1·K-1,M—气体分子量,空气为28.8×10-3kg·mol-1,T —绝对温度,273K+T℃。
近似公式为:C=C0+0.607×T℃式中:C0为零度时的声波速度332m/s;T为实际温度(℃)。
实例:例如当温度0℃时超声波速度是332m/s, 30℃时是350m/s空气中音速与温度的关系式:V=331×根号(1+T/273)(m/S)T:是摄氏温度;V:在T℃时的音速也有介绍音速与温度的关系:音速也是声速,即声音在介质中传播之速度.音波可以在固体、液体或是气体介质中传播,介质密度愈大,则音速愈快.在空气中,音速又会依空气状态(如湿度、温度、密度)不同而有不同数值.如摄氏零度海平面音速约为331.5m/s(1193 km/h);一万米高空音速约为295m/s(1062km/h);另外每升高1摄氏度,音速就增加0.607m/s.温度越高,音速越大.人们经过反复测试,发现水中声速受温度影响.海水里含有盐类,含盐的多少也对声速有影响.在各种因素中,温度对声速影响最大,每升高1℃,水中声速大约增大4.6米/秒.一般认为海水中的声速是1500米/秒,约是大气中声速的4.5倍.科学家们还测出了各种液体里的声速.在20℃时,纯水中的声速是1482.9米/秒;水银中的声速是1451米/秒;甘油中的声速是1923米/秒;酒精中的声速是1168米/秒,四氯化碳液体中的声速是935米/秒.由此可见,声音在液体中传播大都比在大气中传播快许多,这和液体中的分子比较紧密有关.固体中的声速也各不相同,经过反复测定发现,声波在固体中用纵波和横波两种形式传播,这两种波的波速也不相同.例如,在不锈钢中,纵波速度是5790米/秒,横波速度是3100米/秒.把不锈钢做成棒状,棒内的纵波速度是5000米/秒.在金属中,铍是传声的能手,在用铍做的棒内,声波的纵波速度达到12890米/秒,是大气声递的38倍.聚乙烯塑料传声本领较差,聚乙烯棒中的纵波速度只有920米/秒,不及水中声速快.软橡胶富有弹性,声波在里边走不动,速度只有30-50米/秒,还不及空气中的声速呢!通过对波动方程的解的分析已经看到,在§ 3.2 推导媒质状态方程时引入的,出现在波动方程里的常数 c 0 ,原来就是声波的传播速度。

水中声速和温度关系对照表
水的声速和温度是完全相关的,它们受温度的变化而不断变化着。
以下是水中
声速和温度关系对照表:
温度 / 声速
-1℃ / 1498米/秒
4℃ / 1486米/秒
12℃ / 1475米/秒
20℃ / 1460米/秒
28℃ / 1448米/秒
实际上,每一种物质都有自己特定的声速,而水是温度和维度变化很快的材料,其声速并不固定,它随温度变化而变化。
在不同的温度下,水中的声速也会出现不同的变化,可以按照如上表格数据所示来表述。
此类变化,正是水在有声环境中如此受欢迎的理由之一,因为它令声音具有松
弛感,更能表达情绪。
水的声速改变,既可以增加带来的舒适感,也可以减少吵杂的噪音,从而增加了水的魅力所在。
另外,水的声速随温度变化也很有用,从气象学家监测天气变化有关的方面尤
为有效。
他们可以从水中声速变化,以及对应温度变化中得出有价值的信息。
例如,当水声速变慢,表示相应的温度会下降,这是温度降落的一个重要指标,就这样水的声速变化能够帮助气象检测有关的预报及警报情况。
总而言之,水的可变声速使它在娱乐领域有着无限的想象空间,在气象学法中
也有着很重要的作用。
水的声速和温度间的联系表明了它们之间十分密切的关系,已为社会、科学以及决策做出了重要贡献。


声的传播速度和频率声波是一种机械波,它通过介质(如空气、水或固体)的振动传播。
声的传播速度和频率是声波传播过程中的两个重要参数。
一、声的传播速度声的传播速度是指声波在介质中传播的速度。
不同介质的声速不同,通常用符号v表示。
声速的大小取决于介质的性质,如介质的密度、弹性模量和泊松比等。
1.空气中的声速:在常温常压下(0°C,1个大气压),空气中的声速约为343米/秒。
声速在空气中的大小还与空气的温度、压力和湿度等因素有关。
空气温度越高,声速越快;空气压力越大,声速也越快。
2.水中的声速:水中声速约为1480米/秒。
声速在水中的大小还与水的温度、盐度和深度等因素有关。
水温越低,声速越快;水中盐度越高,声速也越快。
3.固体中的声速:固体中的声速一般比空气和水中的声速快。
在钢铁中,声速约为5000米/秒;在橡胶中,声速约为40-150米/秒。
二、声的频率声的频率是指声波振动的次数,通常用符号f表示,单位是赫兹(Hz)。
频率表示声波的音高,频率越高,声音听起来越尖锐;频率越低,声音听起来越低沉。
1.人耳的听觉频率范围:人耳能够听到的声波频率范围大约是20Hz到20000Hz。
低于20Hz 的声波称为次声波,高于20000Hz的声波称为超声波。
2.声波的波长和频率的关系:根据波动方程,声波的波长(λ)与声速(v)和频率(f)之间的关系为:λ = v/f。
即波长与声速成正比,与频率成反比。
三、声的传播速度和频率的关系声的传播速度和频率之间没有直接的关系,但它们之间存在间接的影响。
在同一介质中,声速是一定的,当声波的频率发生变化时,其波长也会发生变化。
1.声波在介质中的传播:声波在介质中传播时,遇到不同密度的介质界面,会发生反射、折射和透射等现象。
这些现象会影响声波的传播速度和频率。
2.声波的多普勒效应:当声源和观察者相对运动时,观察者接收到的声波频率会发生变化,这就是多普勒效应。
多普勒效应说明了声的传播速度和频率之间的关系。
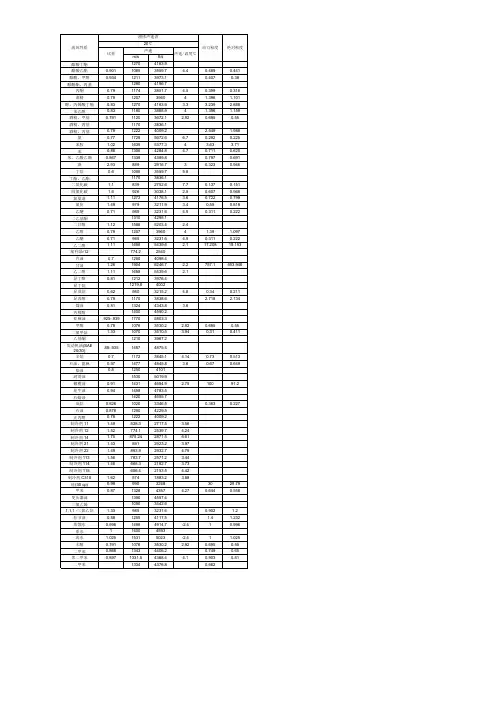
声速与温度之间存在正比关系,即随着温度的升高,声速也会相应增加。
这是因为温度升高会导致空气分子的平均速度增加,进而使得声波在空气中的传播速度加快。
这种关系可以用一个简单的数学公式来表示:v = (331.3 + 0.606t) m/s,其中v表示声速,单位为米每秒,t表示温度,单位为摄氏度。
这个公式适用于0~100摄氏度之间的温度范围。
从这个公式可以看出,声速与温度之间的关系是线性的,温度每升高1摄氏度,声速就会增加约0.606米每秒。
除了温度,声速还受到其他因素的影响,如湿度和气压。
湿度越高,空气中的水蒸气含量就越多,这会导致空气密度和粘度的增加,从而影响声速。
气压对声速的影响较小,但在相同温度和湿度下,气压越高,声速也会稍微增加。
总的来说,声速与温度之间的关系是密切的,而且是正比的。
这种关系在气象学、声学、物理学等领域都有广泛的应用。
例如,在气象学中,声速的测量可以用于推算空气中的温度分布,这对于天气预报和气象研究具有重要意义。
公式也是有一定的误差的,具体如下已知超声波速度与温度的关系如下:式中: r —气体定压热容与定容热容的比值,对空气为1.40,R —气体普适常量,8.314kg·mol-1·K-1,M—气体分子量,空气为28.8×10-3kg·mol-1,T —绝对温度,273K+T℃。
近似公式为:C=C0+0.607×T℃式中:C0为零度时的声波速度332m/s;T为实际温度(℃)。
实例:例如当温度0℃时超声波速度是332m/s, 30℃时是350m/s空气中音速与温度的关系式:V=331×根号(1+T/273)(m/S)T:是摄氏温度;V:在T℃时的音速也有介绍音速与温度的关系:音速也是声速,即声音在介质中传播之速度.音波可以在固体、液体或是气体介质中传播,介质密度愈大,则音速愈快.在空气中,音速又会依空气状态(如湿度、温度、密度)不同而有不同数值.如摄氏零度海平面音速约为331.5m/s(1193 km/h);一万米高空音速约为295m/s(1062km/h);另外每升高1摄氏度,音速就增加0.607m/s.温度越高,音速越大.人们经过反复测试,发现水中声速受温度影响.海水里含有盐类,含盐的多少也对声速有影响.在各种因素中,温度对声速影响最大,每升高1℃,水中声速大约增大4.6米/秒.一般认为海水中的声速是1500米/秒,约是大气中声速的4.5倍.科学家们还测出了各种液体里的声速.在20℃时,纯水中的声速是1482.9米/秒;水银中的声速是1451米/秒;甘油中的声速是1923米/秒;酒精中的声速是1168米/秒,四氯化碳液体中的声速是935米/秒.由此可见,声音在液体中传播大都比在大气中传播快许多,这和液体中的分子比较紧密有关.固体中的声速也各不相同,经过反复测定发现,声波在固体中用纵波和横波两种形式传播,这两种波的波速也不相同.例如,在不锈钢中,纵波速度是5790米/秒,横波速度是3100米/秒.把不锈钢做成棒状,棒内的纵波速度是5000米/秒.在金属中,铍是传声的能手,在用铍做的棒内,声波的纵波速度达到12890米/秒,是大气声递的38倍.聚乙烯塑料传声本领较差,聚乙烯棒中的纵波速度只有920米/秒,不及水中声速快.软橡胶富有弹性,声波在里边走不动,速度只有30-50米/秒,还不及空气中的声速呢!。
水中声速和温度关系的实验研究超声波是一种研究液体分子物理特性及其化学特性的简易方法,早在20世纪70年代人们就重视用超声波进行液体分子物理及其相关性质的研究[1-5],90年代又有不少研究报道[6-9]。
但是声速随温度变化复杂,需要我们做进一步的探索。
本文利用时差法来测量了超声波在液体中的传播特性。
下面具体介绍利用超声波测定声波在水中的传播速度随温度变化的测量原理和测量方法。
2实验原理2.1 时差法测量声速时差法测量声速是利用已知声波传播的距离,测量发射脉冲和接收脉冲之间的时间差。
计算出声速在液体中的传播速度,即超声波 [10] (1)时差法其中▽L的是位移之差,▽T是传播所用的时间。
在储液槽中注入液体,直至将换能器完全浸没,但不能超过液面线。
注意:注入液体时,不能将液体淋在数字显示表头上。
将专用信号源上的“声速传播介质”置于“液体”位置,换能器的连接端应在接线盒上的“液体”专用插座上。
测量液体声速时,由于在液体中声波的衰减较小,因而存在较大的回波叠加,并且在相同频率的情况下,其波长要大得多,用驻波法和相位法测量时可能会有较大的误差,所以建议采用时差法测量。
2.2 陶瓷换能器工作原理频率在20Hz~20kHz的机械波振动在弹性介质中的传播就形成超声波超过20KH超声波,超声波的传播速度就是声波的传播速度,而超声波长短,易于定向发射等优点[11],声速实验声速所采用的声波频率一般都在20~60kHz之间。
此频率范围内,采用压电陶瓷换能器作为声波的发射器,接收效果最佳。
压电陶瓷换能器根据它的工作方式,分为纵向(振动)换能器。
声速教学实验中大多数采用纵向换能器。
图3为纵向换能器的结构,用示波器观察波谷和波峰,或观察两个波间的相位差,原理是正确的,但读数位置不易确定。
较精确测量声速是用声波时差法。
时差法在工程中得到了广泛的应用,它是将经脉冲调制的电信号加到发射换能器上,声波在介质中传播,经过时间后,到达距离处的接收陶瓷换能器图2水中声速与温度关系的实验研究3 实验方法3.1 时差法测量声速操作方法(1)实验时只要按图3连接中换能器的S2该接在信号源的S2上,再把信号源上的Y1,Y2顺次与示波器上的Y1,Y2接通即可。
温度与声速的公式嘿,说起温度与声速的公式,这可真是个有趣又有点复杂的玩意儿。
咱们先来讲讲温度对声速的影响到底是咋回事儿。
温度越高呀,空气分子就越活跃,它们传递声音的速度也就跟着加快啦。
这就好比一群小朋友在操场上跑步,天气热的时候,他们跑得更带劲,速度也就更快。
那这温度与声速之间的公式到底是啥呢?这公式就是 v = 331 +0.6T ,这里的 v 代表声速,单位是米每秒,T 呢就是温度,单位是摄氏度。
比如说,在 0 摄氏度的时候,把 T = 0 带进公式里,算出来声速 v大概就是 331 米每秒。
要是温度升高到 20 摄氏度,那把 T = 20 带进去,算出来声速就约是 343 米每秒啦。
我记得有一次,在一个大热天,我走在公园里。
周围的蝉鸣声此起彼伏,那声音感觉比平时更响亮、更急促。
我当时就想到了温度与声速的关系。
你想啊,那天的温度那么高,空气里的分子都像兴奋的小精灵,欢快地传递着声音,所以蝉鸣声听起来就更加响亮和迅速。
再比如说,咱们冬天在室外说话,声音好像就没那么有“穿透力”,传播得好像也没那么快。
这就是因为温度低,声速变慢啦。
咱们生活里还有很多和这公式相关的有趣现象呢。
像坐飞机的时候,高空的温度低,声速也会发生变化。
这对飞机的噪音传播都有影响呢。
还有啊,在一些特殊的工业环境里,比如高温的车间,工人们交流的时候,声音传播的特点也会因为温度的变化而有所不同。
总之,温度与声速的公式虽然看起来只是几个简单的数字和符号,但它背后隐藏着好多和我们生活息息相关的有趣现象。
了解了这个公式,能让我们对身边的声音世界有更深入的认识和理解,是不是还挺有意思的?希望通过我这番讲解,能让您对温度与声速的公式有更清楚的了解,感受到科学就在咱们身边,无处不在。