同济大学流体力学实验 能量方程实验报告

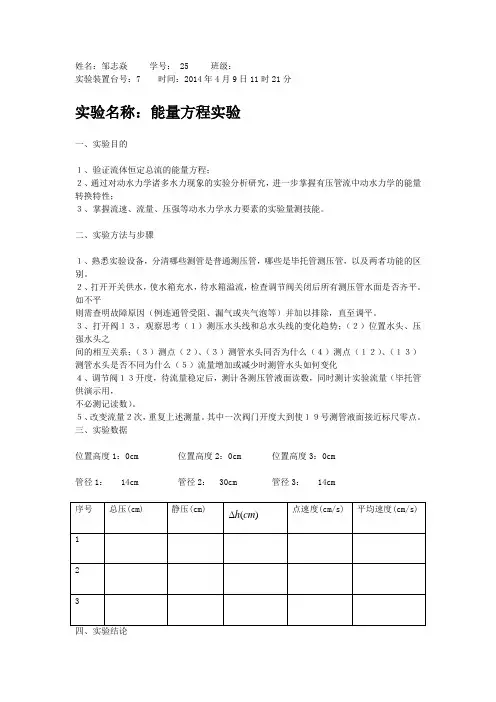
姓名：邹志焱学号： 25 班级：实验装置台号：7 时间：2014年4月9日11时21分实验名称：能量方程实验一、实验目的１、验证流体恒定总流的能量方程；２、通过对动水力学诸多水力现象的实验分析研究，进一步掌握有压管流中动水力学的能量转换特性；３、掌握流速、流量、压强等动水力学水力要素的实验量测技能。

二、实验方法与步骤１、熟悉实验设备，分清哪些测管是普通测压管，哪些是毕托管测压管，以及两者功能的区别。

２、打开开关供水，使水箱充水，待水箱溢流，检查调节阀关闭后所有测压管水面是否齐平。

如不平则需查明故障原因（例连通管受阻、漏气或夹气泡等）并加以排除，直至调平。

３、打开阀１３，观察思考（１）测压水头线和总水头线的变化趋势；（２）位置水头、压强水头之间的相互关系；（３）测点（２）、（３）测管水头同否为什么（４）测点（１２）、（１３）测管水头是否不同为什么（５）流量增加或减少时测管水头如何变化４、调节阀１３开度，待流量稳定后，测计各测压管液面读数，同时测计实验流量（毕托管供演示用，不必测记读数）。

５、改变流量２次，重复上述测量。

其中一次阀门开度大到使１９号测管液面接近标尺零点。

三、实验数据位置高度1：0cm 位置高度2：0cm 位置高度3：0cm管径1： 14cm 管径2： 30cm 管径3： 14cm四、实验结论122221(72.15813010)3.8910 6.55229.8v h cm g --⨯+=⨯+=⨯ 222222(15.71443710)3.8010 3.93229.8v h cm g --⨯+=⨯+=⨯ 222233(72.15813010)3.4510 6.11229.8v h cm g --⨯+=⨯+=⨯ 在不考虑水头损失的情况下，1,2,3处的总水头约相等。

加上水头损失，1,2,3处的水头相等，即能量守恒:212P v Z g γ++=常数。

1. 验证不可压缩流体定常流的能量方程；2. 通过对流体动力学诸多水力现象的实验分析研讨，进一步掌握有压管流中的能量转换特性；3. 掌握流速、流量、压强等动水力学水力要素的实验量测技能。

二、实验原理能量方程是流体力学中的一个重要方程，它描述了流体在流动过程中能量守恒的规律。

对于不可压缩流体定常流，能量方程可表示为：\[ \rho (u^2 + v^2 + w^2) + g(z_2 - z_1) = \rho \left( \frac{du}{dt} + u \frac{d}{dx} + v \frac{d}{dy} + w \frac{d}{dz} \right) + \frac{\partial \tau}{\partial x} + \frac{\partial \tau}{\partial y} + \frac{\partial\tau}{\partial z} \]其中，\( \rho \) 为流体密度，\( u \)、\( v \)、\( w \) 分别为流体在 \( x \)、\( y \)、\( z \) 方向上的流速，\( g \) 为重力加速度，\( z \) 为流体高度，\( \tau \) 为应力张量。

三、实验装置1. 实验台：由实验管道、测压管、皮托管、调节阀等组成；2. 测量仪器：流速仪、流量计、压强计等；3. 计算机及数据采集系统。

四、实验步骤1. 熟悉实验装置，了解各部件的功能及操作方法；2. 检查实验管道是否畅通，测压管、皮托管等是否安装正确；3. 打开水源，调节阀门，使流体在实验管道中流动；4. 在实验管道的不同位置设置测点，测量各测点的流速、流量、压强等数据；5. 根据测量数据，计算各截面的能量值；6. 对比计算结果与理论值，验证能量方程的正确性。

（此处应列出实验过程中测得的流速、流量、压强等数据，以及计算得到的能量值）六、实验结果与分析1. 通过实验，验证了不可压缩流体定常流的能量方程的正确性；2. 通过对实验数据的分析，进一步掌握了有压管流中的能量转换特性；3. 通过实验，提高了对流速、流量、压强等动水力学水力要素的实验量测技能。

附加：实验前用实验报告纸写好预习报告，预习报告包括下方实验内容中的：实验目的、实验内容、数据记录及整理（表格一定要画），报告只写“能量方程实验”！“雷诺实验”暂时不写能量方程实验一、实验目的1．观察流体流经能量方程实验管时的能量转化情况，并对实验中出现的现象进行分析，从而加深对能量方程的理解。

2．掌握一种测量流体流速的方法。

二、实验内容1．测出能量方程实验管的四个断面四组测压管的液柱高度，并利用计量水箱和秒表测定流量。

2．根据测试数据和计算结果，绘出某一流量下的各种水头线，并运用能量方程进行分析，解释各测点各种能头的变化规律。

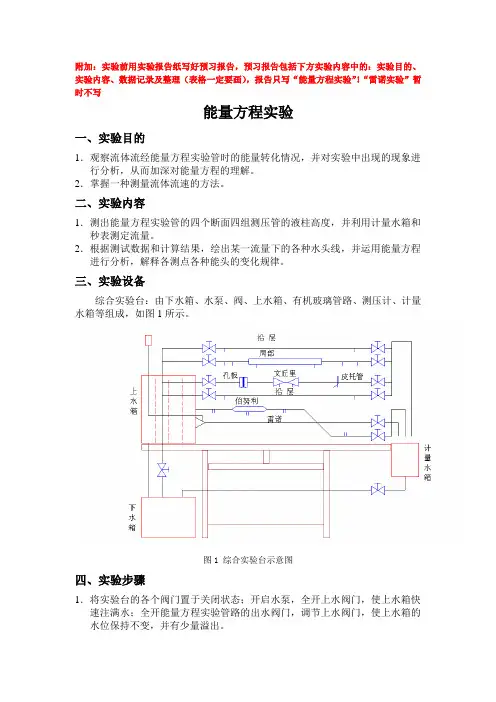
三、实验设备综合实验台：由下水箱、水泵、阀、上水箱、有机玻璃管路、测压计、计量水箱等组成，如图1所示。

图1 综合实验台示意图四、实验步骤1．将实验台的各个阀门置于关闭状态；开启水泵，全开上水阀门，使上水箱快速注满水；全开能量方程实验管路的出水阀门，调节上水阀门，使上水箱的水位保持不变，并有少量溢出。

2．关闭能量方程实验管路的出水阀门，此时能量方程试验管的四个断面四组测压管的液柱应位于同一高度，此为起始总水头，记入数据表中。

3．调节能量方程实验管路的出水阀门至某一开度(工况1)，测定能量方程试验管的四个断面四组测压管的液柱高度，并利用秒表和计量水箱测定流量，记入数据表中。

4．改变能量方程实验管路的出水阀门的开度(工况2)，测定能量方程试验管的四个断面四组测压管的液柱高度，并利用秒表和计量水箱测定流量，记入数据表中。

5．整理实验数据。

五、注意事项数据测定必须待流体流动稳定时方可读数。

六、数据记录及整理1．实验数据记录计量水箱底面积A(cm2)：表1 流量测定数据记录及整理表2．实验数据整理 (1) 体积流量：()tAh h Q 12-=m 3/s注意：式中h 1、h 2的单位为m ，A 的单位为m 2，t 的单位为s 。

(2) 速度水头h ∆=总压水头-测压管水头能量损失=前后断面总压水头之差(3) 平均流速：24dQU π= m/s轴心流速：h g V ∆=2 m/s注意：式中Q 的单位为m 3/s ，d 的单位为m ，h ∆的单位为m 。

流体力学动量方程实验报告流体力学动量方程实验报告引言：流体力学是研究流体运动规律的学科，其中动量方程是描述流体运动的基本方程之一。

本实验旨在通过实验验证流体力学动量方程，并探究不同因素对流体运动的影响。

实验设备与方法：1. 实验设备：本实验使用的设备包括流体力学实验装置、流速计、压力计等。

2. 实验方法：首先，将流体力学实验装置设置在水平台面上，并校准流速计和压力计。

然后，通过调节装置中的阀门控制流体的流速和压力。

在实验过程中，记录不同条件下的流速和压力数据，并进行数据处理。

实验结果与分析：1. 流体速度与动量的关系：在实验中，我们通过改变流体的流速，记录了不同流速下的动量数据。

结果显示，流体的动量与流速成正比关系。

这符合流体力学动量方程中的基本原理，即动量等于质量乘以速度。

2. 流体压力与动量的关系：在实验中，我们通过改变流体的压力，记录了不同压力下的动量数据。

结果显示，流体的动量与压力成正比关系。

这也符合流体力学动量方程中的基本原理，即动量等于质量乘以速度。

3. 流体密度与动量的关系：在实验中，我们通过改变流体的密度，记录了不同密度下的动量数据。

结果显示，流体的动量与密度成正比关系。

这同样符合流体力学动量方程中的基本原理。

4. 流体粘度对动量的影响：在实验中，我们通过改变流体的粘度，记录了不同粘度下的动量数据。

结果显示，流体的动量与粘度成反比关系。

这是因为高粘度的流体阻力大，导致动量的损失较大。

结论：通过本实验，我们验证了流体力学动量方程，并研究了不同因素对流体运动的影响。

实验结果表明，流体的动量与流速、压力、密度和粘度等因素密切相关。

这对于理解和预测流体运动具有重要意义，也为相关工程应用提供了理论依据。

未来展望：在今后的研究中，可以进一步探究其他因素对流体运动的影响，如温度、流道形状等。

同时，可以结合数值模拟方法，对流体力学动量方程进行更深入的研究，以提高流体力学理论的准确性和应用价值。

结语：通过本实验，我们对流体力学动量方程有了更深入的理解。

一、实验目的1. 理解能量方程的基本概念和原理。

2. 掌握能量方程的实验操作方法。

3. 通过实验验证能量方程的正确性。

二、实验原理能量方程是描述物体在运动过程中能量转化和守恒的数学表达式。

在本次实验中，我们通过实验验证能量方程在特定条件下的正确性。

实验原理如下：1. 动能定理：物体所受合外力做的功等于物体动能的变化。

2. 势能定理：物体在重力场中的势能变化等于重力所做的功。

3. 能量守恒定律：在一个封闭系统中，能量既不会凭空产生，也不会凭空消失，只会从一种形式转化为另一种形式。

三、实验器材1. 弹簧振子装置2. 量角器3. 计时器4. 秒表5. 天平6. 米尺7. 记录本四、实验步骤1. 调整弹簧振子装置，使其处于平衡位置。

2. 使用量角器测量弹簧振子的初始角度θ0。

3. 将弹簧振子拉至初始角度θ0，然后释放。

4. 使用计时器记录弹簧振子运动过程中的时间t。

5. 使用秒表记录弹簧振子从最高点到最低点的时间t1。

6. 使用天平测量弹簧振子的质量m。

7. 使用米尺测量弹簧振子的最大位移x。

8. 记录实验数据。

五、数据处理1. 计算弹簧振子的角速度ω：ω = θ0 / t2. 计算弹簧振子的线速度v：v = x / t13. 计算弹簧振子的动能Ek：Ek = 1/2 m v^24. 计算弹簧振子的势能Ep：Ep = m g x5. 计算弹簧振子的总能量E：E = Ek + Ep6. 根据实验数据，分析能量方程的正确性。

六、实验结果与分析1. 实验数据如下：初始角度θ0：10°时间t：2.5s时间t1：0.5s质量 m：0.2kg最大位移x：0.1m重力加速度g：9.8m/s^22. 计算结果：角速度ω：0.004 rad/s线速度v：0.2 m/s动能Ek：0.02 J势能Ep：0.02 J总能量E：0.04 J3. 分析：通过实验数据，我们可以看到弹簧振子的动能和势能在运动过程中相互转化，但总能量保持不变。

流体力学能量方程实验报告流体力学能量方程实验报告：1.实验背景：流体力学能量方程是研究流体静力学和流体动力学的重要概念之一。

在流体力学中，能量是流体的重要属性，涉及到流体的各种物理特性和运动规律的研究。

因此，开展流体力学能量方程的实验，对于加深对流体力学理论的理解具有重要意义。

2.实验目的：本实验旨在通过对流体的能量方程的观测和测量，研究流体的能量变化与流体速度和压力的关系，并探究流体动力学中的基本特性和动态规律。

3.实验过程及结果：在实验过程中，我们通过使用流量计、压力计、热量计等工具，对流体的速度、流量、压力和温度等进行测量，并观察流体在管道中的流动特性。

通过实验的数据分析和处理，我们得到了以下一些重要的实验结果：(1) 流体的速度与压力之间存在直接的关系，速度越大，压力越小；(2) 流体的流量与管道内壁面的摩擦和管道截面积大小有关，流量越大，管道壁面的摩擦越大； (3) 流体的温度和压力也是密切相关的，流体在管道中的温度和压力在变化的过程中，能量也随之发生明显的变化。

4.实验结论：流体力学能量方程是流体力学领域中重要的基本概念之一，通过实验测量和数据分析，我们可以更加深入地了解流体的运动规律和性质，并进一步探究流体动力学中的各种特性和规律。

流体力学能量方程实验对于深化流体力学的基础理论和技术应用具有重要的推动作用，有助于进一步提高流体力学研究的水平和实验能力。

5.实验误差及改进措施：在实验中，由于流体本身的特性和实验条件的限制，可能会导致一些误差和不确定性。

例如，在测量流体速度和压力时可能存在实验仪器的误差以及管道内流体的湍流现象等。

为了减小这些误差，我们可以使用更高精度的仪器、采用稳定实验环境、增加实验次数和平均值方法等措施来提高实验结果的可靠性和精度。

6.实验启示：本实验不仅深化了我们对流体力学能量方程的理解和认识，还使我们掌握了一定的实验技能和科学实验方法。

此外，实验还启示我们在学习和研究各种科学理论和技术的过程中，应注重理论与实践相结合，采用全面、严谨的科学实验方法，加强团队合作和交流学习，共同推进科学研究和学术进步。

一、实验目的1. 了解流体在管内流动时，静压能、动能、位能之间相互转换的关系。

2. 深入理解伯努利方程，掌握其应用。

3. 培养学生运用实验方法验证理论知识的能力。

二、实验原理伯努利方程是描述流体在管道中流动时能量守恒的方程。

该方程表明，在不可压缩、不可压缩流体中，沿流动方向，流速增加时，静压能减小，动能增加；流速减小时，静压能增加，动能减小。

同时，流体在流动过程中，位能、动能和静压能之和保持不变。

伯努利方程可表示为：\[ P + \frac{1}{2} \rho v^2 + \rho gh = \text{常数} \]其中，P为流体压强，ρ为流体密度，v为流速，g为重力加速度，h为流体高度。

三、实验仪器与设备1. 实验装置：伯努利方程演示装置，包括有机玻璃管道、水箱、流量计、压力计等。

2. 数据采集系统：数据采集器、传感器等。

四、实验步骤1. 连接实验装置，检查各部件是否完好。

2. 打开水箱，使水箱充水，待水箱溢流。

3. 调节流量计，控制流量稳定。

4. 在管道上设置不同位置的测压点，用压力计测量各点的压强。

5. 使用数据采集系统记录各测点的压强数据。

6. 改变管道形状（如弯头、缩径等），观察压强变化，分析能量转换情况。

7. 比较不同形状管道的压强分布，验证伯努利方程。

8. 实验结束后，整理实验数据，分析实验结果。

五、实验数据与分析1. 实验数据（1）管道直段：P1 = 0.5 MPa，P2 = 0.4 MPa，v1 = 2 m/s，v2 = 1 m/s，h1 = 1 m，h2 = 1.5 m。

（2）管道弯头：P3 = 0.3 MPa，P4 = 0.4 MPa，v3 = 1 m/s，v4 = 2 m/s，h3 = 1 m，h4 = 1.5 m。

（3）管道缩径：P5 = 0.6 MPa，P6 = 0.5 MPa，v5 = 1 m/s，v6 = 2 m/s，h5 = 1 m，h6 = 1.5 m。

2. 实验结果分析根据实验数据，我们可以发现：（1）在管道直段，流速增加时，静压能减小，动能增加；流速减小时，静压能增加，动能减小。

能量方程实验报告能量方程实验报告引言：能量是物理学中的一个重要概念，它描述了物体或系统的能力进行工作。

能量方程是研究能量转化和守恒的重要工具。

本实验旨在通过测量和分析能量转化过程中的各个因素，验证能量方程的有效性。

实验目的：1. 了解能量的基本概念和能量方程的原理；2. 使用简单的实验装置，验证能量方程的有效性；3. 分析实验数据，探讨能量转化的规律。

实验装置：1. 弹簧秤：用于测量物体的重力；2. 温度计：用于测量物体的温度变化；3. 电热器：用于提供热能；4. 试管：用于装载实验物体。

实验步骤：1. 将试管装满水，并用弹簧秤称量其质量；2. 将试管放置于电热器上，通过电热器提供热能，使水温升高；3. 同时使用温度计测量水温的变化；4. 当水温达到一定值后，关闭电热器，继续测量水温的变化；5. 记录实验数据，包括水的质量、初始温度、最终温度以及升温过程中的时间。

实验结果与分析：根据实验数据，我们可以计算出水的热容和温度变化对应的能量转化。

根据能量方程，能量转化可以表示为：能量转化 = 热容× 质量× 温度变化通过实验数据的分析，我们可以得出以下结论：1. 在升温过程中，水的热容保持不变；2. 随着水温的升高，能量转化的大小也增加；3. 在关闭电热器后，水温仍会继续升高，这是因为水分子的热运动仍会继续，从而继续转化为热能；4. 实验结果与理论计算相符，验证了能量方程的有效性。

结论：通过本实验，我们验证了能量方程在能量转化过程中的适用性。

能量方程可以用于描述能量的转化和守恒，帮助我们理解能量在物理系统中的作用。

同时，本实验还提醒我们在实际应用中要注意能量的转化损失，以提高能量利用效率。

进一步讨论：本实验只考虑了水的热容对能量转化的影响，实际上，在不同物质和系统中，能量转化的过程可能受到其他因素的影响，例如化学反应、摩擦等。

未来的研究可以进一步探索这些因素对能量转化的影响，并优化能量转化的过程，以提高能源利用效率。

流体力学动量方程实验报告流体力学实验报告(全)工程流体力学实验报告实验一流体静力学实验实验原理在重力作用下不可压缩流体静力学基本方程或(1.1)式中：z被测点在基准面的相对位置高度；p被测点的静水压强，用相对压强表示，以下同；p0水箱中液面的表面压强；γ液体容重；h被测点的液体深度。

另对装有水油（图1.2及图1.3）U型测管，应用等压面可得油的比重S0有下列关系：(1.2)据此可用仪器（不用另外尺）直接测得S0。

实验分析与讨论1.同一静止液体内的测管水头线是根什么线？测压管水头指，即静水力学实验仪显示的测管液面至基准面的垂直高度。

测压管水头线指测压管液面的连线。

实验直接观察可知，同一静止液面的测压管水头线是一根水平线。

2.当PB0时，试根据记录数据，确定水箱内的真空区域。

，相应容器的真空区域包括以下三部分：(1)过测压管2液面作一水平面，由等压面原理知，相对测压管2及水箱内的水体而言，该水平面为等压面，均为大气压强，故该平面以上由密封的水、气所占的空间区域，均为真空区域。

(2)同理，过箱顶小水杯的液面作一水平面，测压管4中，该平面以上的水体亦为真空区域。

(3)在测压管5中，自水面向下深度某一段水柱亦为真空区。

这段高度与测压管2液面低于水箱液面的高度相等，亦与测压管4液面高于小水杯液面高度相等。

3.若再备一根直尺，试采用另外最简便的方法测定γ0。

最简单的方法，是用直尺分别测量水箱内通大气情况下，管5油水界面至水面和油水界面至油面的垂直高度h和h0，由式，从而求得γ0。

4.如测压管太细，对测压管液面的读数将有何影响？设被测液体为水，测压管太细，测压管液面因毛细现象而升高，造成测量误差，毛细高度由下式计算式中，为表面张力系数；为液体的容量；d为测压管的内径；h 为毛细升高。

常温(t=20℃)的水，=7.28dyn/mm，=0.98dyn/mm。

水与玻璃的浸润角很小，可认为cosθ=1.0。

于是有(h、d单位为mm)一般来说，当玻璃测压管的内径大于10mm时，毛细影响可略而不计。

能量方程演示实验一．实验目的1、观察恒定流情况下，水流所具的位置势能、压强势能和动能，以及在各种边界条件下能量的守恒和转换规律，加深对能量方程物理意义的理解。

2、观察测压管水头线和总水头线沿程变化的规律，以及水头损失现象。

3、观察管流中的真空现象及渐变流过水断面与急变流过水断面上的动水压强分布规律二、实验设备本实验台由高位水箱、供水箱、水泵、有机玻璃实验管道、铁架等部件组成。

三．实验原理过水断面的能量由位能、压能、动能三部分组成。

水流在不同流径、不同高程的管路中流动时，三种能量不断地相互转化，在实验管道各断面设置测压管及测速管即可演示出三种能量沿程变化的实际情况。

测压管中水位显示的是位能和压力能之和，即能量方程中之前两项:p Z gρ+,测速管中水位显示的是位能、压能、动能之和。

即能量方程中三项之和:22p v Z g gρ++。

将测压管中的水位连成一线，称为测压管水头线,反映势能沿程的变化；将测速管中的水位连成一线，称为总水头线,反映总能量沿程的变化。

两线的距离即为流速水头gv 22。

本实验台在有机玻璃实验管道的关键部位处，设置测压管及测速管，适当的调节流量，就可把总水头线和测压管水头线绘制于测压板上。

四、实验步骤及注意事项（1）开动水泵，将供水箱内之水箱至高位水箱；（2）高位水箱开始溢流后，调节实验管道阀门，使测压管、测速管中水位和测压板上红、黄两线一致；（3）实验过程中，始终应保持微小溢流；（4）如水位和红黄两线不符，有两种可能：一是连接橡皮管中有气泡，可不断用手挤握橡皮管，使气泡排出；二是测速管测头上挂有杂物，可转动测头使水流将杂物冲掉。

五、实验结果1、思考并回答以下问题（1） 总水头线和测压管水头线在局部阻力和沿程阻力处的变化规律；（2） 总水头线沿程下降和测压管水头线升降都有可能的原理；（3） 不同管径流速水头的变化规律。

2、记录数据绘制总水头线和测压管头线。

同济大学流体力学实验报告静水压强实验和伯努利方程实验前言流体力学是一门实用性很强的学科，它研究的对象是流体中的运动和相应的力学问题，其广泛应用于水利、水电、船舶、机械、化工等各个领域。

为了更好地理解流体力学，本次实验我们进行了静水压强实验和伯努利方程实验。

一、实验目的1.了解静水压强的概念及其计算方法。

2.了解流体静压力的产生原理。

3.掌握用皮托管和风洞测量差压的方法。

4.理解伯努利方程的物理意义。

5.熟悉伯努利方程的实验方法及结果分析。

二、实验原理1.静水压强实验原理静水压强是指静止不动的流体所产生的压强，它是由于流体分子间的相互作用力所产生的压强。

在静止的流体中，由于流体的不可压缩性和流体分子的连续性，任何一点处的压强都是相等的。

静水压强公式为P=ρgh，其中ρ为流体的密度，g是重力加速度，h是液体的压头。

液体的压强只与液体高度有关，与液体横截面积无关。

2.伯努利定理实验原理伯努利方程是流体力学中的重要定理，它是热力学第一定律在流体中的应用，描述了在流体中沿着流线的稳恒流动中，流体的总能量守恒。

伯努利方程的数学形式为：P1+1/2ρv1²+ρgh1=P2+1/2ρv2²+ρgh2，其中P1、v1、h1为流体在点1处的压强、速度和位置，P2、v2、h2为流体在点2处的压强、速度和位置。

3.实验器材(1) 双口皮托管：测量速度压强。

(2) 多孔板：掩盖直线流动的速度分布，使得速度分布在整个试验区内保持恒定。

(3) 一个风洞(4) 数字压力计：测量压强差。

(5) 液位计：测量流体的高度。

三、实验步骤1. 静水压强实验(1) 将实验装置包括双口皮托管、数字压力计、液面计等连接起来。

(2) 把双口皮托管放置在液体里，保证口向上，在关闭口塞之前，先打开两口塞的短小孔，確認双口管内外的压力相同。

(3) 关闭型式口塞和长小孔，使双口管的两个端口分别与数字压力计连接，并依次对三个接口进行防漏。

不可压缩流体恒定流能量方程（伯努利方程）实验一、实验背景1726年，伯努利通过无数次实验，发现了“边界层表面效应”：流体速度加快时,物体与流体接触的界面上的压力会减小，反之压力会增加。

为纪念他的贡献，这一发现被称为“伯努利效应”。

伯努利效应适用于包括气体在内的一切流体,是流体作稳定流动时的基本现象之一，反映出流体的压强与流速的关系，即在水流或气流里，如果速度大，压强就小，如果速度小，压强就大。

1738年，在他的最重要的著作《流体动力学》中，伯努利将这一理论公式化，提出了流体动力学的基本方程，后人称之为“伯努利方程”。

书中还介绍了著名的伯努利实验、伯努利原理，用能量守恒定律解决了流体的流动问题，这对流体力学的发展，起到了至关重要的推动作用。

伯努利简介丹尼尔伯努利（Daniel Bernouli,1700～1782），瑞士物理学家、数学家、医学家，被称为“流体力学之父”。

1700年2月8日生于荷兰格罗宁根，1782年3月17日逝世于巴塞尔。

他是伯努利这个数学家族（4代10人）中最杰出的代表，16岁时就在巴塞尔大学攻读哲学与逻辑，后获得哲学硕士学位。

17～20岁时，违背家长要他经商的愿望，坚持学医，并于1721年获医学硕士学位，成为外科名医并担任过解剖学教授。

他在父兄熏陶下最后仍转到数理科学。

伯努利在25岁时应聘为圣彼得堡科学院的数学院士，8年后回到瑞士的巴塞尔，先任解剖学教授，后任动力学教授，1750年成为物理学成教授。

他还于1747年当选为柏林科学院院士，1748年当选为巴黎科学院院士，1750年当选英国皇家学会会员。

在1725～1749年间，伯努利曾十次荣获法国科学院的年度奖。

除流体动力学这一主要领域外，丹尼尔·伯努利的研究领域极为广泛，他的工作几乎对当时的数学和物理学的研究前沿的问题都有所涉及。

他最出色的工作是将微积分、微分方程应用到物理学，研究流体问题、物体振动和摆动问题，因此他被推崇为数学物理方法的奠基人．二、实验目的要求1．验证流体恒定总流的能量方程；2．通过对动水力学诸多水力现象的实验分析，进一步掌握有压管流中动水力学的能量转换特性；3．掌握流速、流量、压强等动水力学水力要素的实验量测技能。

流体力学能量方程实验一、引言流体力学能量方程是研究流体内部能量转换和传递的重要方程。

在实验中，通过测量不同位置的温度、压力等参数，可以验证能量方程的正确性和适用性。

本文将介绍流体力学能量方程实验的相关内容。

二、实验原理1. 能量守恒定律在物理学中，能量守恒定律是指系统内部能量总和不会发生改变，只会从一种形式转换为另一种形式。

在流体力学中，能量守恒定律可以表示为：∂(ρE)/∂t + ∇·(ρE+P)u = ∇·q + ρf·u其中，ρ是密度，E是单位质量的总能量（包括内能和动能），P是压力，u是速度矢量，q是热通量密度（即单位时间内通过单位面积的热流），f是外力矢量。

2. 流体力学实验装置为了验证流体力学能量方程的正确性和适用性，在实验中需要使用相应的装置。

常见的流体力学实验装置包括：(1) 热传导管：用于测量流体中不同位置的温度。

(2) 压力传感器：用于测量流体中不同位置的压力。

(3) 流量计：用于测量流体在管道中的流速。

(4) 热电偶：用于测量流体中不同位置的温度。

三、实验步骤1. 准备工作在进行实验之前，需要进行一些准备工作，包括：(1) 确定实验装置和材料。

(2) 按照实验要求搭建好实验装置。

(3) 校准各种传感器和仪器。

2. 实验操作在进行实验操作时，需要按照以下步骤进行：(1) 开始记录时间，并打开流体进口阀门，使流体开始流动。

(2) 在不同位置测量温度、压力等参数，并记录下来。

可以使用热传导管、压力传感器、热电偶等仪器进行测量。

(3) 根据测得的数据计算出能量守恒方程中各项的值，并绘制出相应的图表。

(4) 分析数据，验证能量方程的正确性和适用性。

可以比较实验结果与理论计算结果之间的差异，或者通过对实验数据进行拟合来验证能量方程的适用性。

四、注意事项在进行流体力学能量方程实验时，需要注意以下事项：(1) 实验过程中需要保持实验装置和测量仪器的稳定性，避免外界因素对实验结果的影响。

伯努利能量方程实验指导书一、实验目的1、观察流体流经能量方程试验管的能量转化情况，对实验中出现的现象进行分析，加深对能量方程的理解。

2、掌握一种测量流体流速的方法。

3、验证静压原理。

二、实验装置实验装置如图1所示，在实验桌上方放有稳压水箱、实验管路、毕托管、测压管、压差板、控制阀门和计量水箱。

实验桌的侧下方则放置有供水箱及水泵。

图 1三、实验原理不停运动着的一切物质，所具有的能量也在不停转化。

在转化过程中，能量只能从一种形式转化为另一种形式，即遵守能量守恒定律。

流体和其他物质一样，也具有动能和势能两种机械能，流体的动能与势能之间，机械能与其它形式的能量之间，也可互相转化，其转化关系，同样遵守能量转换守恒定律。

当理想不可压缩流体在重力场中沿管线作定常流动时，流体的流动遵循伯努力里能量方程。

即常数=2u 2g +γp +Z式中：z —位置水头压力水头速度水头p γ2g u 2实际流体都是有粘性的，因此在流动过程中由于磨擦而造成能量损失。

此时的能量方程变为：其中能量损失hw是由沿程磨擦损失hf和局部能量损失hj两部分组成。

本实验就是通过观察和测量对流体在静止与流动时上述的能量转化与守恒定律的验证。

四、实验操作1、验证静压原理：启动水泵，等水罐满管道后，关闭两端阀门，这时观察能量方程实验管上各个测压管的液柱高度相同，因管内的水不流动没有流动损失，因此静止不可压缩均布重力流体中，任意点单位重量的位势能和压力势能之和保持不变，测点的高度和测点的前后位置无关。

2、测速：能量方程实验管上的每一组测压管都相当于一个皮托管，可测得管内任意一点的流体点速度，本实验台已将测压管开口位置设在能量方程实验管的轴心，故所测得动压为轴心处的，即最大速度。

根据以上公式计算某一工况各测点处的轴心速度和平均流速添入表格，可验证出连续性方程。

对于不可压缩流体稳定的流动，当流量一定时，管径粗的地方流速小，细的地方流速大。

3、观察和计算流体、流径，能量方程实验管对能量损失的情况：在能量方程实验管上布置四组测压管，每组能测出全压和静压，全开阀门，观察总压沿着水流方向的下降情况，说明流体的总势能沿着流体的流动方向是减少的，改变给水阀门的开度，同时计量不同阀门开度下的流量及相应的四组测压管液柱高度，进行记录和计算。

一、实验目的1. 理解能量方程的基本原理和适用条件。

2. 掌握能量方程在流体力学中的应用，验证其在实际流体运动中的正确性。

3. 通过实验，加深对动能、势能和压力能之间相互转换关系的理解。

4. 培养实验操作技能，提高分析问题和解决问题的能力。

二、实验原理能量方程是描述流体在流动过程中能量守恒的方程。

对于不可压缩流体，能量方程可表示为：ρ(u²/2 + gz + p/ρg) = const其中，ρ为流体密度，u为流速，g为重力加速度，z为流体高度，p为压力，g为重力加速度。

能量方程表达了在流体流动过程中，动能、势能和压力能之间的相互转换关系。

当流体在管道中流动时，由于管道内径、流速、压力等参数的变化，能量在不同形式之间进行转换。

三、实验仪器与设备1. 能量方程实验仪：包括有机玻璃管道、阀门、测压计、流量计等。

2. 水箱：用于提供实验流体。

3. 水泵：用于驱动流体流动。

4. 计算器：用于数据处理和计算。

四、实验步骤1. 连接实验仪：将有机玻璃管道、阀门、测压计、流量计等连接好，确保各部件连接牢固。

2. 调整实验参数：打开阀门，使水箱充水，待水箱溢流，检查调节阀关闭后所有测压管水面是否齐平。

如不平，则需查明故障原因（例连通管受阻、漏气或夹气泡等）并加以排除，直至调平。

3. 实验数据采集：调节阀门开度，待流量稳定后，测计各测压管液面读数，同时测计实验流量。

4. 改变流量：改变流量，重复上述测量。

5. 数据处理：将实验数据整理成表格，计算动能、势能和压力能，分析能量转换关系。

五、实验结果与分析1. 实验数据：实验数据如表1所示。

表1 实验数据实验次数 | 流量Q(m³/h) | 位置高度z(m) | 压力p(Pa) | 动能u²/2(Pa) | 势能gz(Pa) | 压力能p/ρg(Pa)--------|--------------|---------------|------------|----------------|-------------|----------------1 | 0.1 | 0.5 | 1.5 | 0.05 | 4.9 | 9.82 | 0.2 | 0.5 | 1.5 | 0.1 | 4.9 | 9.83 | 0.3 | 0.5 | 1.5 | 0.15 |4.9 | 9.82. 能量转换关系分析：从实验数据可以看出，在实验过程中，动能、势能和压力能之间存在以下关系：（1）动能与流量成正比，即流量增加，动能也随之增加。