x
F
y
x+y)/2 x-y)/2 x
设x面和y面的应力分别为 D( x , x ), E ( y , y ),
由于 x
y ,
故DE中点坐标
C(
x
2
y
,
0)
为圆心,DE为直径。
29
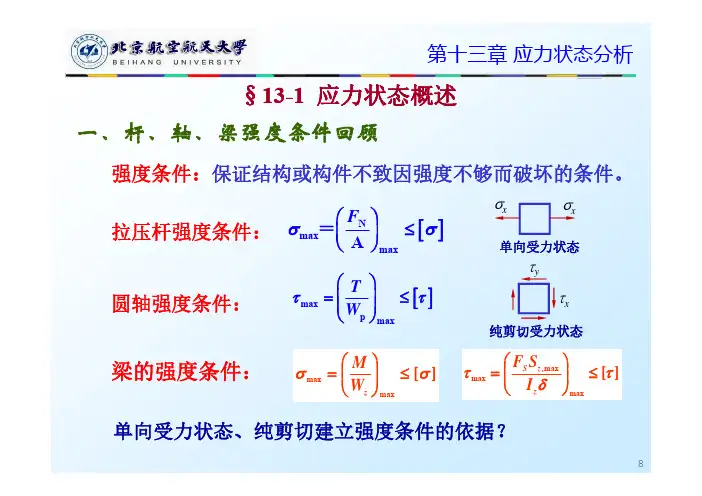
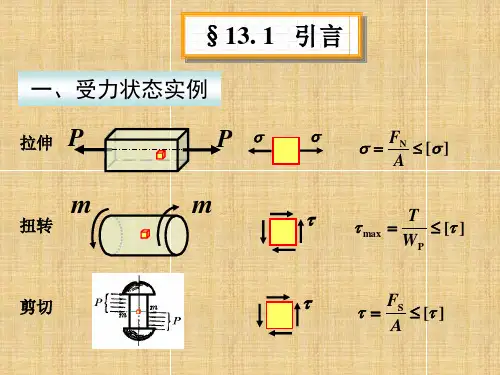
第十三章 应力状态分析
y
y y
n
x
x x
D
C x
o
y
F
绘图:以ED为直径,C为圆心作圆
y
面应力: 考察D点逆时针转动2α
2
60 cos60
=8.35MPa
还可取何值 150; 30 (x轴向左)
N 180 不改变 25
第十三章 应力状态分析
二、应力圆
一、应力圆
应力转轴公式
x
2
y
x
2
y
cos2
xsin2
x
2
y
sin2
xcos2
在 平面上, , 的轨迹?
应力转轴公式形式变换
x
2
推论:微体互垂截面,对应应力圆同一直径两端 微体平行对边, 对应应力圆同一点
32
第十三章 应力状态分析
几种简单受力状态的应力圆
单向受力状态
x
x
纯剪切受力状态 y
x
E 0,0
o
R=x/2
C
D x ,0
D 0,
R=x
o
双向等拉
C
o
x/2
D 0,
45º方向面上既有正应力又有 45º方向面上只有正应力无剪 剪应力,但正应力不是最大 应力,且正应力最大。 值,剪应力却最大。