下载文档原格式
SHANGHAI UNIVERSITY工程中的数值分析方法课程论文COURSE (THESIS)题目:底部剪力法和振型分解反应谱法比较分析学院土木工程系专业建筑与土木工程学号 15722学生姓名芮指导教师朱杰江日期 2016年 3月5日底部剪力法和振型分解反应谱法比较分析朱杰江，（上海大学，上海，200000）摘要:工程中，多自由度弹性体系水平地震作用的计算一般采用振型分解反应谱法，在一定的条件下还可以采用简化的振型分解反应谱法即底部剪力法。
为验证抗震设计规范对底部剪力法和振型分析法的适用条件和范围的规定，用C++编写Jocabi 法程序，对五层均匀、五层非均匀、八层均匀、八层非均匀、十层均匀和十层均匀结构进行了比较分析，证实了规范的正确性，并给出了新的规律。
关键词:抗震；底部剪力法；振型分解法；C++；Jocabi法中图分类号：TU 443文献标识码：AComparative analysis between equivalent base shear method and modal analysismethodZHUJiejiang,Rui Zheng Qing(Shanghai university,200000)Abstract: In engineering, the calculation of multi degree of freedom elastic system generally adopts horizontal seismic action model analysis method，under certain conditions can also be simplified by using the model analysis method--bottom shear method.In order to vertify the rule of application conditions and range about bottom shear method and modal analysis method in earthquake resistant design code, this article has compared and analysed five-storey uniform, five-storey nonuniform, eight-storey uniform, eight-storey nonuniform, ten-storey uniform and ten-storey nonuniform structure by Jocabi method through c++ program. The result has confirmed correctness of earthquake resistant design code. And it also give some new regularity.Key words:seismic resistance; bottom shear method; model analysis method; C++; Jocabi method0引言进行建筑结构地震反应分析时，首先要确定结构的计算简图，除少数结构可以简化成单质点体系外，大多数建筑结构（如多、高层建筑，多跨不等高厂房）质量分布比较分散，则应简化为多质点体系进行分析。
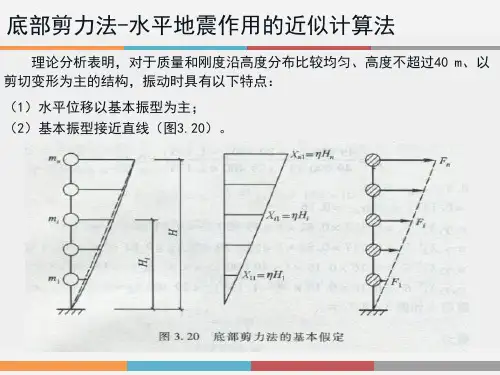
简述确定结构地震作用的底部剪力法的基本原理适用范围和步骤1. 引言1.1 概述底部剪力法是一种常用的结构抗震设计方法，通过对结构底部的剪力进行控制和分配，以提高结构的整体抗震性能。
它基于结构地震作用的特点和结构体系的响应机制，能够较为准确地评估结构在地震作用下的抗震性能，并为工程实践中的建筑设计提供依据。
1.2 文章结构本文将详细介绍底部剪力法的基本原理、适用范围和步骤。
首先，我们将阐述底部剪力概念以及影响结构地震作用的因素；其次，我们将介绍底部剪力法的基本原理及其推导过程；接着，我们将讨论底部剪力法适用范围，并讨论建筑类型、结构形式和地震烈度等因素对其限制；最后，我们将给出底部剪力法的具体步骤，包括确定设计地震加速度谱和周期参数、计算结构质量和弹性刚度分布情况以及确定结构基底剪力分配系数并进行抗震验算。
最后，我们将对底部剪力法的基本原理和适用范围进行总结，并展望其在工程实践中的应用前景。
1.3 目的本文旨在清晰地介绍底部剪力法的基本原理、适用范围和步骤，以帮助读者更好地理解和运用该方法进行结构抗震设计。
通过阐述其基本原理和推导过程，读者可以深入了解底部剪力法的内涵；而讨论其适用范围和局限性则有助于读者准确地选择适合的场景应用该方法；最后，给出的具体步骤可以指导读者在实际工程项目中应用底部剪力法进行抗震设计。
通过本文的阐述，我们希望提高读者对底部剪力法及其应用的认识水平，并促进该方法在工程实践中的广泛应用。
2. 底部剪力法的基本原理2.1 底部剪力的概念底部剪力是指地震作用下，建筑结构底部承受的水平力。
在结构设计中，底部剪力是一个重要的参数，它能够直接体现结构在地震作用下的抗震性能。
2.2 结构地震作用的影响因素对于一个建筑结构来说，其受到地震作用的程度取决于多个因素。
其中包括建筑物所处的地区地震烈度、土壤条件、结构和材料等因素。
这些因素会直接影响到结构所承受的地震力大小及其分布情况。
2.3 底部剪力法的基本原理及其推导过程底部剪力法是一种常用的简化方法，用于确定结构在地震作用下底部所承受的最大水平力。
结构抗震设计相关问题探讨李楚舒 刘春明 李永双（中国建筑标准设计研究院北京金土木软件技术有限公司北京 100044）[提要]根据我国《建筑抗震设计规范》（GB50011-2001）和《高层建筑混凝土结构技术规程》（JGJ3-2002）对抗震设计（如双向地震作用、偶然偏心等问题）和结构扭转不规则控制（周期比、位移比）的相关规定，从结构分析与结构动力学的相关概念出发，结合工程设计实践遇到的具体问题，剖析了相关问题的理论依据，并提出了相应的计算解决方法。
[关键词]抗震设计双向地震作用偶然偏心扭转不规则周期比位移比Discussions on Structural Seismic Design/Li Chushu, Liu Chunming, Li Yongshuang (China Institute of Building Standard Design & Research, Beijing Civil King Software Technology Co., Ltd., Beijing 100044, China) Abstract: According to the requirements on seismic design (such as dual directional seismic action, occasional eccentricity, etc.) and control of torsional irregularity of structure (ratio of period and ratio of displacement) in Code for Seismic Design of Buildings (GB50011—2001) and Technical Specification for Concrete Structure of Tall Buildings (JGJ3—2002), to present the theory basis and solutions in this paper by analyzing and discussing the relative topics on these both in the conceptions of structural analysis and structural dynamics and in the practices in engineering.Keywords: seismic design; dual directional seismic actions; occasional eccentricity; torsional irregularity; ratio of period; ratio of displacement我国建筑结构设计2002规范是对89规范的一次全面修订，在新规范的使用过程中，工程设计人员遇到了许多由于新规范的改进而带来的争议和困惑的问题。
抗震规范底部剪力法计算总结一、计算地震影响系数α1、根据《抗震》附录A 查城市的地震分组、烈度、及基本地震加速度2、根据地震分组地震烈度和多遇地震、罕遇地震，《抗震》表5.1.4-1查αmax3、根据地震分组（第一组）和场地类型（Ⅳ），《抗震》表5.1.4-2查T g 8度9度罕遇地震增加0.05S4、判断Tg< T1< 5 Tg 及，确定计算公式及2η 和γ注：除有专门规定外，建筑结构的阻尼比ζ应取0.05。
这时γ=0.9，η1=0.02，η2=1.0。
5、 最终确定α二、 重力荷载代表值 表格5.1.3楼顶计算 楼板 +下半层墙体重力+活荷载×0+雪荷载×0.5+积灰荷载×0.5每层计算 楼板+上下半墙重量+等效均布活载×0.5（书库、档案活载×0.8）+实际情况的楼活载×1.0 高层 G eq =0.85 G e单层是去1.00三、 顶部的附加力5.2.1确定顶部附加系数确定顶部附加力四、屋面突出的女儿墙、烟囱就、屋顶间的地震作用效应（见施岚青145页例题）1、屋面算作一个个体，N+1个楼层进行计算2、N+13或者《高规》B.0.3五、 剪力的计算1、顶部附加力加入顶层剪力2、剪力自上而下进行叠加3、第N+1层乘以系数4、第N 层（楼的顶层）作用叠加时候，N+1层的剪力不要系数5、遇到框架要剪力进行左右分配六、 考虑地基与结构相互影响，剪力折减 5.2.7 施岚青151夹页并列1、 8度、9度2、 Ⅲ、Ⅳ类场地3、 箱基或刚性较好的筏基和桩基联合基础4、 钢筋混凝土高层建筑剪力折减和层间变形按折减剪力计算七、 验算楼层最小地震剪力 5.2.5八、 计算弯矩标准值及设计值 完全不考虑剪力增大（见施岚青150页例题）九、 计算剪力或弯矩设计值1.3或者地震作用分项系数表5.4.1 )(s T 01.0g T g T 50.6αmax2αηmax45.0αmax2)(αηαγT T g=max12)]5(2.0[αηηαγg T T --=。
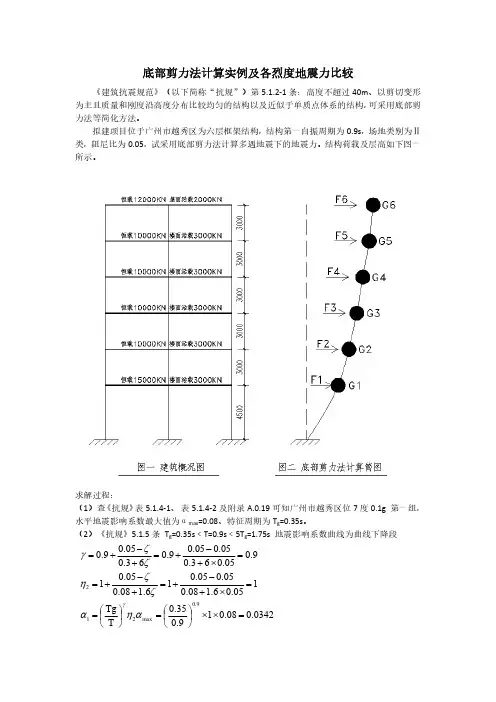
底部剪力法计算实例及各烈度地震力比较《建筑抗震规范》（以下简称“抗规”）第5.1.2-1条：高度不超过40m 、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构以及近似于单质点体系的结构，可采用底部剪力法等简化方法。
拟建项目位于广州市越秀区为六层框架结构，结构第一自振周期为0.9s ，场地类别为Ⅱ类，阻尼比为0.05，试采用底部剪力法计算多遇地震下的地震力。
结构荷载及层高如下图一所示。
求解过程：（1）查《抗规》表5.1.4-1、表5.1.4-2及附录A.0.19可知广州市越秀区位7度0.1g 第一组，水平地震影响系数最大值为αmax =0.08、特征周期为T g =0.35s 。
（2）《抗规》5.1.5条T g =0.35s ﹤T=0.9s ﹤5T g =1.75s 地震影响系数曲线为曲线下降段0342.008.019.035.0T Tg 105.06.108.005.005.016.108.005.019.005.063.005.005.09.063.005.09.09.0max 212（3）重力荷载代表值计算，《抗规》5.1.3条可知屋面活荷载不计入，楼面活荷载组合系数为0.5，则各层重力荷载代表值如下图三所示：图三：楼层G1G2G3G4G5G6重力荷载代表值（KN ）165001150011500115001150012000总和（KN ）74500（4）《抗规》5.2.1条对于多质点结构等效重力荷载取重力荷载代表值的85%，故Geq=0.85×74500=63325KN ；T g =0.35s T 1=0.9s>1.4T g =0.49s δn =0.08T 1+0.07=0.08×0.9+0.07=0.142KN53.30772.2165142.0F F 1F HG H G F KN 72.2165633250342.0G F EK n n n EK n1j iiii i eq 1EK）（各层地震力F i 计算结果如下图四所示图四：楼层G i （KN ）H i （m ）G i H i∑H j G j F i （KN ）61200019.5234000860250812.8151150016.5189750409.7841150013.5155250335.2831150010.5120750260.772115007.586250186.26116500 4.574250160.35（5）楼层剪力V i 计算如下图五所示，根据《抗规》5.2.2条 nij EKi jV 7度λ=0.016图五：楼层F i （KN ）G i （KN ）V i （KN ）λ∑G j Vi>λ∑G j 是否满足6812.8112000812.81192满足5409.78115001222.59376满足4335.28115001557.87560满足3260.77115001818.64744满足2186.26115002004.90928满足1160.35165002165.251192满足以上为底部剪力法计算全过程，仅供大家参考，如有疑问欢迎探讨。
抗震底部剪力法要点抗震底部剪力法要点（1）、确定该建筑的抗震等级。
根据《建筑工程抗震设防分类标准》GB50223-2021-6.0.8条，本建筑工程为为未成年人教育类用房，其抗震设防分类标准为重点设防类。
根据《建筑工程抗震设防分类标准》GB50223-2021-3.0.3条，抗震设防烈度需要提高1度采取抗震措施，但计算地震作用时不用提高！根据抗规-2021-6.1.2条：本框架结构的高度2×4.5=9m，抗震设防烈度需要提高1度采取抗震措施：按7+1=8度查抗震等级，查表6.1.2得：该框架结构的抗震等级为二级。
箍筋的最小直径查表得：dmin8mm；(3)但是题目已知：框架梁端纵向受拉钢筋配筋率为2.18%>2%！根据抗规-2021-6.3.3条：表中箍筋的最小直径应增大2mm，故实际采用的箍筋的最小直径为：dmin10mm！《建筑工程抗震设防分类标准》GB50223-2021公共建筑和居住建筑6.0.1 本章适用于体育建筑、影剧院、博物馆、档案馆、商场、展览馆、会展中心、教育建筑、旅馆、办公建筑、科学实验建筑等公共建筑和住宅、宿舍、公寓等居住建筑。
6.0.2 公共建筑，应根据其人员密集程度、使用功能、规模、地震破坏所造成的社会影响和直接经济损失的大小划分抗震设防类别。
6.0.3 体育建筑中，规模分级为特大型的体育场，大型、观观席容量很多的中型体育场和体育馆（含游泳馆），抗震设防类别应划为重点设防类6.0.4 文化娱娱建筑中，大型的电影院、剧场、礼堂、图书馆的视听室和报告阀、文化馆的观演阀和展览阀、娱娱中心建筑，抗震设防类别应划为重点设防类。
6.0.5 商业建筑中，人流密集的大型的多层商场抗震设防类别应划为重点设防类。
当商业建筑与其他建筑合建时应分别判断，并按区段确定其抗震设防类别。
6.0.6 博物馆和档案馆中，大型博物馆，存放国家一级文物的博物馆，特级、甲级档案馆，抗震设防类别应划为重点设防类。
有关结构抗震设计底部剪力系数的讨论李楚舒，李立，王龙（北京筑信达工程咨询有限公司，北京100043）摘要：本文推导出底部剪力系数的简洁物理表达及在反应谱曲线上的等效点，依据结构动力学、反应谱理论和结构抗震设计原理等基本理论体系，可以对此系数进行直观定性分析判断；进而探讨在结构抗震设计中应该如何使用最小限值，提出改进对最小底部剪力系数标定的建议。
关键词：结构抗震设计，底部剪力系数，最小底部剪力系数的使用和标定0引言随着我国超高层建筑的迅猛发展，广大工程设计人员和科研工作者针对抗震设计中遇到的“最小地震底部剪力系数”（或“最小剪重比”）问题，进行了有益的讨论，指出《建筑抗震设计规范》GB50011-2010[1]（简称抗规）具体条文规定的一些问题。
文献[2]全面介绍了抗规对最小地震剪力系数取值规定的背景，再次强调了“当不满足规范最小地震剪力系数限值时，对楼层剪力乘以放大系数，只是提高了构件承载力，并不能解决结构体系不合理的问题，应通过调整结构布置、减轻结构质量和提高结构刚度来解决”。
文献[3]从大量超高层设计经验出发，指出“由于结构高度高，周期长，剪重比一般难以满足规范要求”，提出“剪重比限值与特征周期相关联”、“剪重比限值按结构周期分类进一步细分关联”、“通过调整结构总剪力和各楼层水平地震剪力以满足最小剪重比要求”等建议。
文献[4]从功率谱概念出发，指出抗规中“楼层最小地震剪力系数仅与地震影响系数的最大值相关，与场地类别无关，显然是不合理的”，而且“最小剪力系数与结构体系合理性无关”，提出了“加速度反应谱第一下降段按TT−1的规律下降，第二下降段按TT−2的规律下降”的反应谱函数建议。
文献[5]推导出规范最小剪重比限值的内涵是“对应II类场地，质量M，周期T的单质点结构，在TT=3.5 ss 时的基底剪力对最小剪力限值；TT=5.0 ss时，此限值为0.88M质量时单质点结构的最小基底剪力”，给出了其他类别场地的最小剪重比建议值，指出了“欲通过调整结构刚度或重量来满足规范剪重比要求是十分困难的”，“适宜的方法是通过周期折减系数，增大楼层地震剪力，当仍不满足要求时，可将不满足楼层处的地震剪力按规范要求放大（不传递），以满足规范要求”。
文献[6]按抗规及SRSS振型组合法推导出剪重比为“各振型地震影响系数平方与各振型参与质量系数平方乘积之和的二次方根”。
指出：“想要通过调整结构的质量和刚度，以改变计算的最小剪重比，是困难的且代价高昂的”。
文献[7]推导出一维弯曲型和剪切型的匀质悬臂梁的剪重比公式，也指出“剪重比是否满足规范限制，与结构形式和结构布置的合理性没有明显的关系”，提出了“考虑长周期分量修正的加速度反应谱”来替代“剪重比”控制。
作者简介：李楚舒（1970—），男，博士，教授级高工文献[8]推导出与文献[6]相同的底部剪力系数表达式，指出“任何结构都存在一个临界周期，只要结构基本周期超过临界周期，底部剪力系数总不能满足规范要求”、“结构体系和布置方案与底部剪力系数能不能满足最小限值的要求没有明显的关系”、“不满足最小限值并不能说明结构方案布置不合理”；通过与美国规范的对照，指出“抗规的最小剪力系数限值是合理的”；通过四种工程处理方式（刚度控制与强度控制），指出“当不满足最小剪力系数时，合理、简单、有效的方法是按比例放大设计地震作用使其满足要求”，同时建议“最小底部剪力系数的取值应计入场地效应”。
文献[9]通过对某超高层结构采用两种不同的剪力系数控制方法（A：方案满足抗规最小剪重比的要求；B：对不满足的楼层进行剪力放大来满足规范要求）的案例研究表明，“虽然大震弹塑性分析A、B性能相当”，但“A的构件尺寸明显大于B，A的材料用量和设计难度均高于B”，“抗倒塌分析表明，B比A反而具有更高的抗倒塌安全储备”。
综上所述，基本上可以得到三点一致性的结论：（1）剪力系数是结构的本来属性，其大小并不能判定结构方案的优劣；（2）剪力系数最小值应当与场地类别挂钩；（3）不满足规范最小剪力系数，在保证结构构件内力和位移要求的前提下，不应（也很难）通过调整结构方案（质量和刚度）来达到规范要求，应该直接进行地震力放大处理，以保证结构具有相应的安全储备。
本文拟通过结构动力学、反应谱理论和结构抗震设计原理等基本理论体系，得出底部剪力系数的物理表达，便于进行直观定性分析；进而探讨应该在结构抗震设计中如何使用这个限值，及如何改进最小底部剪力系数的标定。
1底部地震剪力系数Chopra将各振型底部剪力等效原则，构建出各振型对应的单自由度系统，来阐释反应谱理论[10]。
依据此思想，可以采用对振型分解反应谱法的底部剪力等效的原则来构建一个等效的单自由度系统，此系统的底部剪力等于原多自由度体系，其等效质量MM eeeeee等于原系统质量M。
与Chopra的方法不同的是，本文不关注各个振型，而直接对经过振型组合后（无论是何种组合方法，SRSS或CQC）的最终结果（底部剪力）进行等效。
这个单自由度系统，反应谱法给出的底部剪力为：VV bb eeeeee=ααeeeeee MMMM (1) 其中：ααeeeeee是在反应谱曲线对应周期TT eeeeee的地震影响系数，MM是重力加速度。
总可以找到这样一个等效周期TT eeeeee来在反应谱曲线上对应ααeeeeee，使得VV bb eeeeee等于原系统振型分解反应谱法得到的底部剪力VV bb。
利用TT eeeeee=2ππ�MM/KK eeeeee关系，也就可以找到等效的刚度KK eeeeee，本文不需要求出等效刚度。
根据基本的结构动力学常识，对于一般结构，动力特性主要由第一振型控制，第一振型的参与质量系数比高阶振型要大得多（假设第一振型的参与质量系数可以达到50%以上的话——这对建筑结构一般不是问题，只要结构顶部不存在特别柔的类似“桅杆”的部分），那么等效周期TT eeeeee与原结构的第一周期（即：基本周期）TT1的关系为：TT eeeeee≥TT1 (2) 一般情况下，式(2)都是取大于符号，在原结构是单自由度体系时会相等。
而且，第一振型参与质量系数越小，TT eeeeee相比TT1就越大。
这也就是抗规底部剪力法（5.2.1条）中对结构等效总重力荷载采用了85%的总重力荷载代表值，来对多质点进行计算的原因。
根据抗规对地震底部剪力系数的定义，对这个等效单自由度系统来讲，底部剪力系数表达为：λλ=VV GG=VV bb eeeeee MMMM=ααeeeeee (3) 式(3)揭示出：任何结构的底部剪力系数都是反应谱曲线上的地震响应系数的对应值。
根据式(2)，可以得知，一般情况下：ααeeeeee≤αα1 (4) αα1为TT1对应的地震影响系数值。
同样，第一振型参与质量系数越小，ααeeeeee相比αα1就越小。
结构自身的特性，如质量分布、刚度分布和结构阻尼比，可以看着是地震剪力系数的“内因”；设计反应谱的具体形式，是可以视为地震剪力系数的“外因”。
由此可见，反应谱法得到的底部地震剪力系数除了是结构自身特性的反映之外，更是反应谱曲线形式的直接作用结果。
图1 设计反应谱曲线上的等效地震影响系数基于反应谱理论，是无法得出底部剪力系数的“合理”的限值范围（如文献[8]给出了一个例子，说明严重不符合结构设计基本力学概念的倒质量、刚度分布，却能“更好”地满足规范剪重比的要求）。
任何结构都可以找到一个对应于反应谱曲线的ααeeeeee。
换言之，不能从ααeeeeee的大小来衡量结构的“优劣”：只要给出了一条具体的反应谱曲线，就能得到对应的ααeeeeee，如图1所示。
图1还说明了这样一个道理：如果对最小底部剪力系数的标定，恰好是反应谱曲线上基本周期的地震影响系数值，那么对于实际的多自由度结构，就会不满足这个标定值。
抗规就是采取II类场地对最小值进行标定的，详见3、4节。
2关于反应谱理论扶长生教授对反应谱理论进行了概括[11]：反应谱理论的杰出贡献在于它结合了随机理论和确定性分析方法，把地震波的频谱特性、结构的自振特性以及地震作用和效应三者有机地联系在一起。
反应谱理论的数学模型是Guass随机过程，基本假定是，一条地震记录波为Guass随机过程集合中的一次事件，设计反应谱是按平稳随机过程理论统计平均的“连续分段光滑”曲线。
按平稳随机过程进行振型组合，振型分解反应谱法得到的地震反应是Guass随机过程集合的期望值。
在廉价的个人电脑出现之前，反应谱法是线性地震分析的标准方法。
虽然反应谱法存在其固有的缺陷（如，反应谱法得到的响应量是其期望值，因此多个响应量之间并不存在物理关联；反应谱法的结果依赖于坐标系的选取，对位移量也不能进行矢量合成，而且对扭转严重的结构，给出的位移比会“失真”——这就是10规范改用“规定水平力”来进行位移比计算的原因。
等等），但，目前绝大多数国家和地区都采用反应谱法进行结构的抗震设计，各国设计规范对复杂结构都有时程分析计算的补充规定。
随着时程记录的丰富与完善，计算机处理速度和存储量的提升，时程分析将逐步成为抗震工程的主要方法。
特定场地上的一条地震加速度时程记录都可以通过从时域到频域的变换来得到对应的加速度反应谱（指定阻尼比），因此，对于一个结构和一条地震时程记录，时程法和反应谱法得到的结构最大响应在随机过程意义上是一致（注意：是这条时程记录变换的反应谱，而非设计反应谱；且结构为线性系统），这是反应谱法的数学基础（可参见文献[12]第15章中时程、SRSS和CQC振型组合的数值对比）。
同样，一条加速度时程记录可以通过积分得到相应的速度时程和位移时程（需要对起始和终止的速度和位移进行归零处理），理论上讲，线性时程分析采用加速度、速度或位移输入，得到的结构响应是一致的。
反应谱是Fourier谱在结构抗震工程意义上的简化，且用到了如下近似关系：SS pppp(ξξ,ωω)=ωωSS dd(ξξ,ωω) (5-1)SS pppp(ξξ,ωω)=ωω2SS dd(ξξ,ωω) (5-2) 上两式中，SS dd,SS pppp,SS pppp分别是位移谱、伪-速度谱和伪-加速度谱（通常，工程上将“伪-”和下标p省略；而且是相对位移谱、相对速度谱和绝对加速度谱的简称）；ξξ,ωω分别是单自由度体系的阻尼比和圆频率。
显然，对于长周期明显的地震记录，采用加速度反应谱，由于乘以ωω2的结果，可以完全“消除”记录中的长周期成分，这就是加速度反应谱针对长周期问题“力不从心”的根本原因[12]。
基于“近些年的地震中，大多数结构倒塌与软场地有关”的事实，不少学者建议“应该考虑使用相对位移谱作为基本形式来进行地震作用计算”[12]。
以位移为基本变量进行动力平衡方程的求解并没有实质数学上的难度，但要收集整理位移时程记录，并将其转换为可实施的设计位移反应谱确实是一项浩大的系统工程。
