九年级数学下册高频考题专训第2课时锐角三角函数

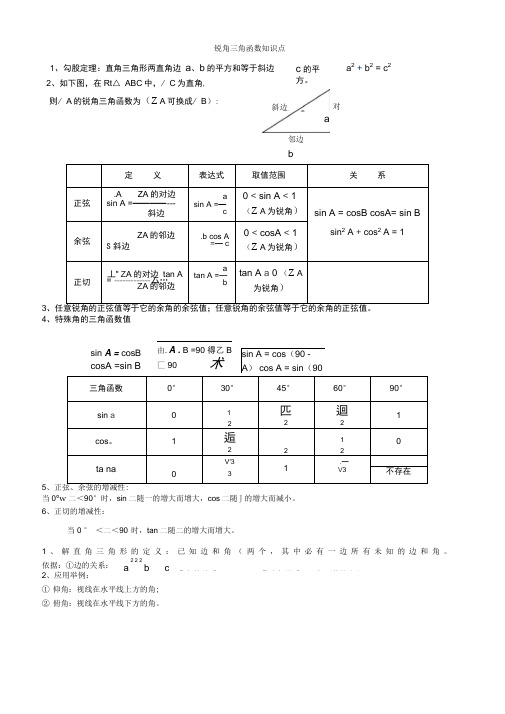
2、如下图，在Rt△ ABC中，/ C为直角,定义表达式取值范围关系正弦.A ZA的对边sin A =————---斜边asin A =—c0 < sin A < 1（Z A为锐角）sin A = cosB cosA= sin Bsin2 A + cos2 A = 1余弦ZA的邻边S斜边.b cos A=—c0 < cosA < 1（Z A为锐角）正切丄“ Z A的对边tan A= ------------- 厶…,Z A的邻边atan A =—btan A a 0 （Z A为锐角）34、特殊角的三角函数值三角函数0°30°45°60°90°sin a012匹2迴21cos。

1逅2212ta naV'31.—03V3不存在5当0°w二＜90°时，sin二随一的增大而增大，cos二随J的增大而减小。

6、正切的增减性：当0 ° ＜二＜90°时，tan二随二的增大而增大。

1、解直角三角形的定义：已知边和角（两个，其中必有一边所有未知的边和角。

依据：①边的关系：2 2 2a b c;②角的关系：A+B=90°;③边角关系：三角函数的定义。

2、应用举例：①仰角：视线在水平线上方的角;②俯角：视线在水平线下方的角。

锐角三角函数知识点1、勾股定理：直角三角形两直角边a、b的平方和等于斜边c的平方。

a2+ b2 = c2则/ A的锐角三角函数为（Z A可换成/ B）:sin A = cosB cosA =sin B 由.A .B =90 得乙B匚90 术sin A = cos（90 -A） cos A = sin（90斜边a邻边b对5、如图，在厶 ABC 中，/ ACB=90 , CD! AB 于 D,若AC二 5 6 , AB =5，则 tan / ACD 的值为()③ 坡面的铅直高度 h 和水平宽度I 的比叫做坡度（坡比）。

九年级下册数学锐角三角函数练习题(2)(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（九年级下册数学锐角三角函数练习题(2)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为九年级下册数学锐角三角函数练习题(2)(word版可编辑修改)的全部内容。

九年级下册数学锐角三角函数练习题一．选择题（共15小题，满分45分，每小题3分)1．(3分）（2015•丽水)如图,点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是（）A．B．C．D．2．（3分）(2015•崇左）如图，在Rt△ABC中，∠C=90°，AB=13，BC=12，则下列三角函数表示正确的是（）A．sinA=B．cosA=C．tanA=D．tanB=3．（3分)（2015•扬州）如图，若锐角△ABC内接于⊙O,点D在⊙O外（与点C在AB同侧），则下列三个结论:①sin∠C＞sin∠D；②cos∠C＞cos∠D；③tan∠C＞tan∠D中,正确的结论为（）A．①②B．②③C．①②③ D．①③4．（3分）(2015•石河子校级模拟）如果∠A为锐角，且sinA=0。

6，那么（）A．0°＜A≤30°B．30°＜A＜45° C．45°＜A＜60° D．60°＜A≤90°5．（3分）(2015•开县二模)在Rt△ABC中，∠C=90°，若,则sinB的值得是（）A．B．C．D．6．（3分）(2015•江夏区模拟）在Rt△ABC中，∠C=90°，sinA=，则tanA的值为（）A．B．C．D．7．（3分）（2015•泰安校级二模）在Rt△ABC中,∠C=90°，若sinA=，则tanB=( ）A．B．C．D．8．（3分）（2015•安陆市模拟）在Rt△A BC中,∠C=90°,sinB=，则cosA的值为( ）A．B．C．D．9．（3分)（2015•玉林）计算：cos245°+sin245°=（）A．B．1 C．D．10．（3分）(2015•天津）cos45°的值等于（)A．B．C．D．11．(3分）（2015•威海）如图，在△ABC中，∠ACB=90°，∠ABC=26°，BC=5．若用科学计算器求边AC的长，则下列按键顺序正确的是（）A．5÷tan26°=B．5÷sin26°=C．5×cos26°=D．5×tan26°=12．（3分）（2015•日照)如图，在直角△BAD中，延长斜边BD到点C，使DC=BD，连接AC，若tanB=,则tan∠CAD的值（）A．B．C．D．13．（3分）（2015•南通）如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（）A．B．C．D．214．（3分)（2015•绵阳）如图，要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时,路灯的灯柱BC高度应该设计为（）A．（11﹣2）米B．(11﹣2）米C．(11﹣2）米D．（11﹣4）米15．（3分)（2015秋•成武县月考）若计算器的四个键的序号如图所示，在角的度量单位为“度的状态下"用计算器求sin47°，正确的按键顺序是（）A．(1)（2）（3）（4） B．（2）（4）（1）（3） C．（1)（4）（2）（3） D．(2）（1）（4）（3）二．填空题（共10小题,满分33分)16．（3分）(2015•曲靖）如图，在半径为3的⊙O中，直径AB与弦CD相交于点E，连接AC，BD，若AC=2，则cosD= ．17．（3分）（2015•成都校级模拟）已知＜cosA＜sin70°，则锐角A的取值范围是．18．（3分）（2015•大连模拟)已知部分锐角三角函数值：sin15°=，sin30°=，sin45°=，sin75°=，计算cos75°=．（提示:sin2x+cos2x=1）19．（3分）（2015•酒泉）已知α、β均为锐角，且满足｜sinα﹣|+=0，则α+β=．20．（3分)（2015•周村区一模）用计算器求tan35°的值,按键顺序是．21．（3分）（2015•齐齐哈尔）BD为等腰△ABC的腰AC上的高，BD=1，tan∠ABD=，则CD的长为．22．（3分）（2015•邵阳）如图，某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B，如果AB=2000米，则他实际上升了米．23．（4分）（2015•西宁）某校数学兴趣小组要测量西山植物园蒲宁之珠的高度．如图，他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C 的仰角为56°，AB=62m，根据这个兴趣小组测得的数据，则蒲宁之珠的高度CD约为m．(sin56°≈0.83，tan56°≈1。

专题28.18 锐角三角函数（中考常考考点专题）（巩固篇）（专项练习）一、单选题【类型一】锐角三角函数【考点一】（正弦✮✮余弦✮✮正切）概念➽➸辨析1．（2021·浙江杭州·一模）在△ABC 中，△C ＝90°，35BC AB =，则（ ）A ．cosA ＝35B ．sinB ＝35C ．tanA ＝43D ．tanB ＝432．（2020·北京市第三十五中学模拟预测）把Rt ABC ∆三边的长度都扩大为原来的3倍，则锐角A 的余弦值（ ）A ．扩大为原来的3倍B ．缩小为原来的13C ．扩大为原来的9倍D ．不变【考点二】角➽➸（正弦✮✮余弦✮✮正切）函数值3．（2021·广东广州·中考真题）如图，在Rt ABC 中，90C ∠=︒，6AC =，8BC =，将ABC 绕点A 逆时针旋转得到A B C '''，使点C '落在AB 边上，连结BB '，则sin BB C ''∠的值为（ ）A ．35B ．45C 5D 25 4．（2022·四川宜宾·中考真题）如图，在矩形纸片ABCD 中，5AB =，3BC =，将BCD △沿BD 折叠到BED 位置，DE 交AB 于点F ，则cos ADF ∠的值为（ ）A ．817B ．715C ．1517D ．815【考点三】（正弦✮✮余弦✮✮正切）函数值➽➸求边长5．（2022·山东菏泽·中考真题）如图，在菱形ABCD 中，2,60AB ABC =∠=︒，M 是对角线BD 上的一个动点，CF BF =，则MA MF +的最小值为（ ）A ．1B 2C 3D ．26．（2022·四川乐山·中考真题）如图，在Rt ABC 中，90C ∠=︒，5BC =，点D 是AC 上一点，连接BD ．若1tan 2A ∠=，1tan 3ABD ∠=，则CD 的长为（ ）A ．25B ．3C 5D ．2【类型二】特殊锐角三角函数【考点一】特殊锐角➽➸函数值 7．（2021·浙江宁波·中考真题）如图，在ABC 中，45,60,B C AD BC ∠=︒∠=︒⊥于点D ，3BD =E ，F 分别为AB ，BC 的中点，则EF 的长为（ ）A 3B 3C ．1D 68．（2016·山东潍坊·中考真题）关于x 的一元二次方程x 22+sin α=0有两个相等的实数根，则锐角α等于（ ）A ．15°B ．30°C ．45°D ．60°【考点二】函数值➽➸特殊锐角9．（2019·湖南怀化·中考真题）已知α∠为锐角，且1sin 2α=，则α∠= （ ） A ．30︒ B ．45︒ C ．60︒ D ．90︒10．（2019·湖北荆州·中考真题）在平面直角坐标系中，点A 的坐标为(3，以原点为中心，将点A 顺时针旋转30︒得到点A '，则点A '的坐标为（ ）A ．)3,1B ．()3,1-C ．()2,1D ．()0,2【考点三】混合运算➽➸特殊锐角✮✮二次根式11．（2013·湖北孝感·中考真题）式子()20002cos30tan 451tan 60-- ） A ．232 B ．0 C ．23D ．012．（2016·浙江杭州·82π327-sin45°中，是有理数的是（ ） A 8B ．2π C 327-D ．sin45°【考点四】特殊锐角值➽➸判断三角形形状13．（2022·安徽淮南·模拟预测）在ABC 中，(22cos 21tan 0A B +-= ，则ABC 一定是（ ）A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形 14．（2019·天津天津·中考模拟）如图，等腰直角ABC ∆中，AC BC =，90ACB ∠=︒，点O 在斜边AB 上，且满足:3BO OA =BOC ∆绕C 点顺时针方向旋转到AQC ∆的位置，则AQC ∠的大小为（ ）A ．100︒B ．105︒C ．120︒D ．135︒【类型三】解直角三角形【考点一】解直角三角形➽➸直接解直角三角形15．（2022·河北·顺平县腰山镇第一初级中学一模）如图，将边长6cm 的正方形纸片沿虚线剪开，剪成两个全等梯形．已知裁剪线与正方形的一边夹角为60°，则梯形纸片中较短的底边长为（ ）A ．（33cmB ．（3﹣3cmC ．（63cmD ．（6﹣3cm 16．（2022·四川·巴中市教育科学研究所中考真题）在平面直角坐标系中，直线33y x =-x 轴交于点A ，与y 轴交于点B ，将AOB 绕O 点逆时针旋转到如图A OB ''△的位置，A 的对应点A '恰好落在直线AB 上，连接BB '，则BB '的长度为（ ）A 3B 3C ．2D 33【考点二】解非直角三角形➽➸转化为直角三角形并解之17．（2020·黑龙江牡丹江·中考真题）如图，在△ABC 中，sinB=13， tanC=2，AB=3，则AC 的长为（ ）A 2B 5C 5D ．218．（2019·内蒙古赤峰·中考真题）如图，点P 是反比例函数(0)k y k x=≠的图象上任意一点，过点P 作PM x ⊥轴，垂足为M ．若POM 的面积等于2，则k 的值等于（ ）．A ．-4B ．4C ．-2D ．2【考点三】解不规则图形➽➸构造直角三角形并解之19．（2020·内蒙古赤峰·中考真题）如图，Rt △ABC 中，△ACB = 90°，AB = 5，AC = 3，把Rt △ABC 沿直线BC 向右平移3个单位长度得到△A 'B 'C ' ，则四边形ABC 'A '的面积是 （ ）A ．15B ．18C ．20D ．2220．（2019·四川达州·中考真题）如图，边长都为4的正方形ABCD 和正三角形EFG 如图放置，AB 与EF 在一条直线上，点A 与点F 重合．现将△EFG 沿AB 方向以每秒1个单位的速度匀速运动，当点F 与B 重合时停止．在这个运动过程中，正方形ABCD 和△EFG 重叠部分的面积S 与运动时间t 的函数图象大致是（ ）A ．B ．C ．D ．【类型四】解直角三角形的应用【考点一】解直角三角形➽➸仰角✮✮俯角21．（2021·重庆·中考真题）如图，在建筑物AB 左侧距楼底B 点水平距离150米的C 处有一山坡，斜坡CD 的坡度（或坡比）为1:2.4i =，坡顶D 到BC 的垂直距离50DE =米（点A ，B ，C ，D ，E 在同一平面内），在点D 处测得建筑物顶A 点的仰角为50°，则建筑物AB 的高度约为（参考数据：sin500.77︒≈；cos500.64︒≈；tan50 1.19︒≈）A ．69.2米B ．73.1米C ．80.0米D ．85.7米22．（2021·山东泰安·中考真题）如图，为了测量某建筑物BC 的高度，小颖采用了如下的方法：先从与建筑物底端B 在同一水平线上的A 点出发，沿斜坡AD 行走130米至坡顶D 处，再从D 处沿水平方向继续前行若干米后至点E 处，在E 点测得该建筑物顶端C 的仰角为60°，建筑物底端B 的俯角为45°，点A 、B 、C 、D 、E 在同一平面内，斜坡AD 的坡度1:2.4i =．根据小颖的测量数据，计算出建筑物BC 的高度约为（ ）（参考数据：3 1.732≈）A ．136.6米B ．86.7米C ．186.7米D ．86.6米【考点二】解直角三角形➽➸方位角23．（2022·河北石家庄·二模）如图，某渔船正在海上P处捕鱼，先向北偏东30°的方向航行10km到A处．然后右转40°再航行53km到B处，在点A的正南方向，点P的正东方向的C处有一条船，也计划驶往B处，那么它的航向是（）A．北偏东20°B．北偏东30°C．北偏东35°D．北偏东40°24．（2022·广东深圳·三模）如图，在距离铁轨200米的B处，观察由深圳开往广州的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东60°方向上；一段时间后，动车车头到达C处，恰好位于B处的西北方向上，则这时段动车的运动路程是（）米（结果保留根号）A．1001003+B．2002003+C．23D．20023【考点三】解直角三角形➽➸坡度坡比25．（2022·广东·广州市第一中学模拟预测）如图，某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4︒，沿山坡向上走到P处再测得该建筑物顶点A的仰角为53︒．已知BC=90米，且B、C、D在同一条直线上，山坡坡度i=5：12，求此人从所在位置点P走到建筑物底部B点的路程（）米.（结果精确到0.1米）（测倾器的高度忽略不计，参考数据：4tan533︒≈，tan63.42︒≈）A．119.2B．137.1C．129.2D．127.1【考点四】解直角三角形➽➸其他问题26．（2021·四川乐山·二模）如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC 是20米，梯坎坡长BC是12米，梯坎坡度i＝13AB的高度为()（精确到0.1236≈2.45）A．30.4B．36.4C．39.4D．45.427．（2022·吉林·长春市绿园区教师进修学校二模）如图，一棵大树被台风拦腰刮断，树根A到刮断点P的距离是4米，折断部分PB与地面成40︒的夹角，那么原来这棵树的高度是（）A．44cos40+︒⎛⎫⎪⎝⎭米B．44sin40+︒⎛⎫⎪⎝⎭米C．()44sin40+︒米D．()44tan40+︒米28．（2022·山东聊城·一模）如图，竖直放置的杆AB，在某一时刻形成的影子恰好落在斜坡CD的D处，而此时1米的杆影长恰好为1米，现量得BC为10米，CD为8米，斜坡CD与地面成30°角，则杆AB的高度为（）A ．(643+米B ．(1043+米C ．8米D ．10米二、填空题 【类型一】锐角三角函数【考点一】（正弦✮✮余弦✮✮正切）概念➽➸辨析29．（2019·陕西师大附中二模）如图，已知第一象限内的点A 在反比例函数25y 的图象上，第二象限内的点B 在反比例数k y x =的图象上且OA OB ⊥，3cos A 则k 的值为________.30．（2021·江苏·宜兴市实验中学二模）如图，点B 在x 的正半轴上，且BA OB ⊥于点B ，将线段BA 绕点B 逆时针旋转60︒到BB '的位置，且点B '的坐标为()1,1．若反比例函数ky x=()0x >的图象经过A 点，则k =______．【考点二】角➽➸（正弦✮✮余弦✮✮正切）函数值 31．（2020·山东菏泽·中考真题）如图，在ABC 中，90ACB ∠=︒，点D 为AB 边的中点，连接CD ，若4BC =，3CD =，则cos DCB ∠的值为______．32．（2020·江苏常州·中考真题）如图，点C 在线段AB 上，且2AC BC =，分别以AC 、BC 为边在线段AB 的同侧作正方形ACDE 、BCFG ，连接EC 、EG ，则tan CEG ∠=_________．【考点三】（正弦✮✮余弦✮✮正切）函数值➽➸求边长 33．（2019·四川广元·中考真题）如图，ABC ∆中，90ABC ︒∠=，2BA BC ==，将ABC ∆绕点C 逆时针旋转60︒得到DEC ∆，连接BD ，则2BD 的值是___．34．（2021·甘肃武威·中考真题）如图，在矩形ABCD 中，E 是BC 边上一点，90,30,AED EAD F ∠=︒∠=︒是AD 边的中点，4cm EF =，则BE =________cm ．【类型二】特殊锐角三角函数【考点一】特殊锐角➽➸函数值35．（2020·上海·中考真题）如图，在△ABC 中，AB =4，BC =7，△B =60°，点D 在边BC 上，CD =3，联结AD ．如果将△ACD 沿直线AD 翻折后，点C 的对应点为点E ，那么点E 到直线BD 的距离为____．36．（2020·贵州遵义·中考真题）如图，对折矩形纸片ABCD 使AD 与BC 重合，得到折痕MN ，再把纸片展平．E 是AD 上一点，将△ABE 沿BE 折叠，使点A 的对应点A ′落在MN 上．若CD ＝5，则BE 的长是_____．【考点二】函数值➽➸特殊锐角37．（2018·四川巴中·中考真题）已知|sinA ﹣122(3tan )B -，那么△A+△B= ． 38．（2012·山东济宁·中考真题）在ABC 中，若△A 、△B 满足|cosA －12|＋(sinB －12)2＝0，则△C ＝____．【考点三】混合运算➽➸特殊锐角✮✮二次根式39．（2022·广西·藤县教学研究室一模）(3)2-⨯312+﹣0(3)40．（2022·山东·潍坊市寒亭区教学研究室一模）计算11|132cos302-⎛⎫-︒+ ⎪⎝⎭的结果是____________．【考点四】特殊锐角值➽➸判断三角形形状41．（2021·贵州黔东南·二模）在ABC 中，2(33)|2cos 30A B -+=，则ABC为________三角形．42．（2021·广东深圳·一模）21cos 302A tanB -=，那么ABC 的形状是_____． 【类型三】解直角三角形【考点一】解直角三角形➽➸直接解直角三角形43．（2022·辽宁大连·中考真题）如图，对折矩形纸片ABCD ，使得AD 与BC 重合，得到折痕EF ，把纸片展平，再一次折叠纸片，使点A 的对应点A '落在EF 上，并使折痕经过点B ，得到折痕BM ．连接MF ，若MF BM ⊥，6cm AB =，则AD 的长是____________cm ．44．（2022·浙江嘉兴·中考真题）如图，在ABC 中，△ABC ＝90°，△A ＝60°，直尺的一边与BC 重合，另一边分别交AB ，AC 于点D ，E ．点B ，C ，D ，E 处的读数分别为15，12，0，1，则直尺宽BD 的长为_________．【考点二】解非直角三角形➽➸转化为直角三角形并解之45．（2018·江苏无锡·中考真题）已知△ABC 中，AB=10，7△B=30°，则△ABC 的面积等于_____．46．（2017·四川绵阳·中考真题）如图，过锐角△ABC 的顶点A 作DE △BC ，AB 恰好平分△DAC ，AF 平分△EAC 交BC 的延长线于点F ．在AF 上取点M ，使得AM =13AF ，连接CM 并延长交直线DE 于点H ．若AC =2，△AMH 的面积是112，则1tan ACH ∠的值是_______．【考点三】解不规则图形➽➸构造直角三角形并解之47．（2010·云南红河·中考真题）如图，在△ABC中，△B=45°，cos△C=，AC=5a，则△ABC的面积用含ａ的式子表示是____ ．48．（2012·黑龙江黑河·中考真题）Rt△ABC中，△A=90°，BC=4，有一个内角为60°，点P是直线AB上不同于A、B的一点，且△ACP=30°，则PB的长为_______．【类型四】解直角三角形的应用【考点一】解直角三角形➽➸仰角✮✮俯角49．（2022·湖北黄石·中考真题）某校数学兴趣小组开展无人机测旗杆的活动：已知无人机的飞行高度为30m，当无人机飞行至A处时，观测旗杆顶部的俯角为30°，继续飞行20m（参考数据：3 1.732，到达B处，测得旗杆顶部的俯角为60°，则旗杆的高度约为________m．结果按四舍五八保留一位小数）50．（2022·江苏南通·中考真题）如图，B为地面上一点，测得B到树底部C的距离为10m，在B处放置1m高的测角仪BD，测得树顶A的仰角为60︒，则树高AC为___________m（结果保留根号）．【考点二】解直角三角形➽➸方位角51．（2022·贵州黔西·中考真题）如图，我海军舰艇在某海域C 岛附近巡航，计划从A 岛向北偏东80°方向的B 岛直线行驶．测得C 岛在A 岛的北偏东50°方向，在B 岛的北偏西40°方向．A ，B 之间的距离为80nmile ，则C 岛到航线AB 的最短距离是_____nmile ．（参考2 1.4≈3 1.7≈）52．（2022·四川绵阳·中考真题）如图，测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量，测量船在A 处测得海岛上观测点D 位于北偏东15°方向上，观测点C 位于北偏东45°方向上，航行半个小时到达B 点，这时测得海岛上观测点C 位于北偏西45°方向上，若CD 与AB 平行，则CD ＝_________海里（计算结果不取近似值）．【考点三】解直角三角形➽➸坡度坡比53．（2022·山东泰安·模拟预测）如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔AB 的高度，他从古塔底部点处前行30m 到达斜坡CE 的底部点C 处，然后沿斜坡CE 前行20m 到达最佳测量点D 处，在点D 处测得塔顶A 的仰角为30︒，已知斜坡的斜面坡度3i =A ，B ，C ，D ，在同一平面内，小明同学测得古塔AB 的高度是___________．54．（2022·山东烟台·一模）一名高山滑雪运动员沿着斜坡FC 滑行，他在点D 处相对大树顶端A 的仰角为30︒，从D 点再滑行210C 点，在点C 处相对树顶端A 的仰角为45︒，若斜坡CF 的坡比为1:3i =（点E ，C ，B 在同一水平线上），则大树AB 的高度___________米（结果保留根号）．【考点四】解直角三角形➽➸其他问题55．（2022·山西太原·二模）如图1是劳动课上同学们组装的一个智能机器臂．水平操作台为l ，底座AB 固定，AB l ⊥，AB 长度为24cm ，连杆BC 长度为30cm ，手臂CD 长度为28cm ，点B ，C 是转动点，且AB ，BC 与CD 始终在同一平面内．如图2，转动连杆BC 和手臂CD ，当135ABC ∠=︒，165BCD ∠=︒时，端点D 离操作台l 的高度DE 为______cm ．56．（2022·河北·石家庄市第四十一中学二模）操作：如图，将四边形纸片ABCD 沿过点A 的直线折叠，使得点B 落在CD 上的点Q 处，折痕为AP ；再将PCQ △，ADQ △分别沿PQ ，AQ 折叠，此时点C ，D 落在AP 上的同一点R 处．请完成下列探究：（1）PAQ ∠的大小为______°；（2）当四边形APCD 是平行四边形时ABQR 的值为______．参考答案1．D【分析】设AB =5a ，BC =3a ，则AC =4a ，然后根据三角函数的定义逐项排查即可． 解：设AB =5a ，BC =3a ，则AC =4a ， 则cosA ＝AC AB＝4455a a =，故A 错误； sinB ＝BC AB ＝4455a a =，故B 错误； tanA ＝4334BC a C a A ==，故C 错误；tanB ＝43AC kBC k=＝43，故D 正确．故选：D ．【点拨】本题主要考查了三角函数的定义和勾股定理，掌握并灵活运用三角函数的定义成为解答本题的关键．2．D【分析】根据相似三角形的性质解答． 解：三边的长度都扩大为原来的3倍， 则所得的三角形与原三角形相似， △锐角A 的大小不变， △锐角A 的余弦值不变， 故选：D ．【点拨】此题考查相似三角形的判定和性质、锐角三角函数的定义，掌握相似三角形的对应角相等是解题的关键．3．C【分析】由勾股定理求出10AB =，并利用旋转性质得出=6AC AC '=，8B C BC '==，90A C C B ∠=∠=''︒，则可求得4BC '=，再根据勾股定理求出45BB '=数的定义即可求得结果．解：在Rt ABC 中，90C ∠=︒，6AC =，8BC =， 由勾股定理得：22226810ABAC BC ．△ABC 绕点A 逆时针旋转得到A B C '''，△=6AC AC '=，8B C BC '==，90A C C B ∠=∠=''︒． △1064BC AB AC ''=-=-=．△在Rt BB C ''△中，由勾股定理得22224845BB BC B C ''''++= △5sin 45BC BB C BB '''∠===' 故选：C ．【点拨】本题考查了求角的三角形函数值，掌握三角形函数的概念并利用勾股定理及旋转的性质求解是解题的关键．4．C【分析】先根据矩形的性质和折叠的性质，利用“AAS”证明AFD EFB ∆∆≌，得出AF EF =，DF BF =，设AF EF x ==，则5BF x =-，根据勾股定理列出关于x 的方程，解方程得出x 的值，最后根据余弦函数的定义求出结果即可．解：△四边形ABCD 为矩形，△CD =AB =5，AB =BC =3，90A C ∠=∠=︒，根据折叠可知，3BE BC ==，5DE DE ==，90∠=∠=︒E C ， △在△AFD 和△EFB 中903A E AFD EFB AD BE ∠=∠=︒⎧⎪∠=∠⎨⎪==⎩，△AFD EFB ∆∆≌（AAS ）， △AF EF =，DF BF =， 设AF EF x ==，则5BF x =-， 在Rt BEF ∆中，222BF EF BE =+， 即()22253x x -=+，解得：85x =，则817555DF BF ==-=，△315cos 17175AD ADF DF ∠===，故C 正确．故选：C ．【点拨】本题主要考查了矩形的折叠问题，三角形全等的判定和性质，勾股定理，三角函数的定义，根据题意证明AFD EFB ∆∆≌，是解题的关键．5．C【分析】连接AF ，则AF 的长就是AM +FM 的最小值，证明△ABC 是等边三角形，AF 是高线，利用三角函数即可求解．解：连接AF，则AF 的长就是AM +FM 的最小值．△四边形ABCD 是菱形， △AB ＝BC ， 又△△ABC ＝60°， △△ABC 是等边三角形， △CF BF = △F 是BC 的中点， △AF △BC ．则AF ＝AB •sin60°＝233= 即MA MF +3 故选：C【点拨】本题考查了菱形的性质，等边三角形以及三角函数，确定AF 的长就是MA MF +的最小值是关键．6．C【分析】先根据锐角三角函数值求出25AC =5,AB =过点D 作DE AB ⊥于点E ，依据三角函数值可得11,,23DE AE DE BE ==从而得32BE AE =，再由5AE BE +=得AE =2，DE =1，由勾股定理得AD 5CD ．解：在Rt ABC 中，90C ∠=︒，5BC = △1tan 2BC A AC ∠== △25,AC BC ==由勾股定理得,2222(25)(5)5AB AC BC ++= 过点D 作DE AB ⊥于点E ，如图，△1tan 2A ∠=，1tan 3ABD ∠=，△11,,23DE DE AE BE == △11,,23DE AE DE BE == △1123AE BE = △32BE AE =△5,AE BE += △352AE AE += △2,AE = △1DE =,在Rt ADE ∆中,222AD AE DE =+ △2222215AD AE DE ++△5,AD CD AC +== △2555,CD AC AD =-= 故选：C【点拨】本题主要考查了勾股定理，由锐角正切值求边长，正确作辅助线求出DE 的长是解答本题的关键．7．C【分析】根据条件可知△ABD 为等腰直角三角形，则BD =AD ，△ADC 是30°、60°的直角三角形，可求出AC 长，再根据中位线定理可知EF =2AC。

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】28.1 锐角三角函数第1课时正弦1. 如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，则∠A的正弦值为（）A．35B．34C．45D．532. 已知在Rt△ABC中，∠C＝90°，sin B＝32，AC＝23，那么AB的长是（）A．33B．32C．3 D．43. 如图，每个小正方形的边长均为1，则图中的△ACB的内角∠ACB的正弦值是（）A．105B．1010C．13D．以上都不对4. 若0°＜∠A＜90°，sin A是方程1(3)04x x⎛⎫--=⎪⎝⎭的根，那么sin A＝．5. 如图，在Rt△ABC，∠ACB=90°，CD⊥AB，AB=15，BD=6，sin A＝33，求CD的长.参考答案1．A 2．D 3．B4．1 45．6228.1 锐角三角函数第2课时锐角三角函数1. 如图，斜坡AB长20米，其水平宽度AC长为103米，则斜坡AB的坡度为（）A．30° B．60° C．33D．122. 如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tan B的值是（）A．45B．35C．34D．433. 已知在Rt△ABC中，∠C＝90°，tan B＝32，BC＝23，那么AC的长是．4. 如图，点E（0，4），O（0，0），C（5，0）在⊙A上，BE是⊙A上的一条弦．则tan∠OBE= ．5．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，BC=2，AB=4，则cos∠ACD的值为．参考答案1．C2．C3．34．4 55．24【解析】∵∠ACB=90°，BC=2，AB=4，∴cos B=24 BCAB.∵⊥，∴∠=90°，∴∠=∠，∴cos∠ACD=cos B2.28.1 锐角三角函数第3课时特殊角的三角函数值1. 直角△ABC中，∠A = 30°，则sin A、 tan A的值分别是（）A．32、33B．12、3C．12、33D．22、332. 下列各式不正确的是（）A．sin30°＝cos60° B．t an45°= 2sin30°C．sin30°＋cos30°＝1 D．t an60°·cos60°＝sin60°3. 在△ABC中，已知∠A、∠B是锐角，且sin A＝32，tan B＝1，则∠C的度数为．4．计算：（1）sin245°＋co s30°·tan60°；（2）22sin45°＋3sin60°－2(tan301)︒-．5. 如图, 在△ABC中, ∠B=45°, ∠C=30°, AB=42, 求A C和BC的长.参考答案1．C 2．C 3．75°4．解：（1）原式＝2231332 2222⎛⎫+⨯=+=⎪⎪⎝⎭．（2）原式＝2233331122233⎛⎫⨯+⨯--=+⎪⎪⎝⎭．5．解：过A作AD⊥BC于D.在Rt△ABD中, AD=BD=AB·sin45°=24242⨯=.在Rt△ACD中, . ∴BC=BD+CD=443+28.1 锐角三角函数第4课时利用计算器求锐角三角函数值和锐角度数1．计算sin20°－cos20°的值是（保留四位有效数字）（）A．－0.5976 B．0.5976C．－0.5977 D．0.59772. Rt△ABC中，∠C=90°，a:b=3:4，运用计算器计算∠A的度数为（精确到1°）（）A．30° B．37° C．38° D．39°3. 用“＞”“＝”“＜”填空：（1）cos37° co s46°；（2）tan41°tan21°；（3）sin31°cos31°．4. 用计算器求值（精确到0.0001）：（1）sin25°－cos25°；（2）sin15°＋cos25°＋tan35°．5. 已知等腰△ABC的底边AB＝20，它的面积为80，求它的顶角大小（精确到1°）．参考答案1．C2．B3．（1）－0.4837 （2）1.86534．（1）＞（2）＞（3）＜5．103°28.2 解直角三角形第1课时解直角三角形1．如图，在△ABC中，∠C＝90°，∠B＝50°，AB＝10，则BC的长为（）A．10tan50°B．10cos50°C．10sin50°D．10 cos502. 如图，矩形ABCD中，对角线AC、BD相交于点O，∠AOB=60°，AB=5，则AD的长是（）A．53 B．52 C．5 D．103．如图，在等腰直角三角形ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=15，则AD的长是（）A．2 B．2 C．1 D．224. 在Rt△ABC中，∠C＝90°．（1）已知AB，∠A，则BC＝，AC＝ ;（2）已知AC，∠A，则BC＝，AB＝ ;（3）已知AC，BC，则tan A＝．5. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD是∠BAC的平分线，与BC相交于点D，且AB＝43，求AD的长.参考答案 1．B 2．A 3．B4．（1）Ab sin A AB cos A （2）AC tan A cos AC A （3）BCAC5. 解：在Rt △ABC 中， ∵∠B ＝30°，∴11432322AC AB ==⨯=． ∵AD 平分∠BAC ，∴在Rt △ACD 中，∠CAD ＝30°，∴3234cos30AC AD ===︒．【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

达标训练基础•巩固1.在Rt △ABC 中，如果各边长度都扩大2倍，则锐角A 的正弦值和余弦值( )A.都没有变化B.都扩大2倍C.都缩小2倍D.不能确定 思路解析：当Rt △ABC 的各边长度都扩大二倍，所得新三角形与原三角形相似，故锐角A 大小不变. 答案：A2.已知α是锐角，且cosα=54，则sinα=( )A.259 B.54 C.53 D.2516 思路解析：由cosα=54，可以设α的邻边为4k ，斜边为5k ，根据勾股定理，α的对边为3k ，则sinα=53. 答案：C 3.Rt △ABC 中，∠C=90°，AC ∶BC=1∶3，则cosA=_______，tanA=_________.思路解析：画出图形，设AC=x ，则BC=x 3，由勾股定理求出AB=2x ，再根据三角函数的定义计算. 答案：21，34.设α、β为锐角，若sinα=23，则α=________；若tanβ=33，则β=_________.思路解析：要熟记特殊角的三角函数值 答案：60°,30°5.用计算器计算：sin51°30′+ cos49°50′-tan46°10′的值是_________. 思路解析：用计算器算三角函数的方法和操作步骤. 答案：0.386 06.△ABC 中，∠BAC=90°，AD 是高，BD=9，tanB=34，求AD 、AC 、BC.思路解析：由条件可知△ABC 、△ABD 、△ADC 是相似的直角三角形，∠B=∠CAD ，于是有tan ∠CAD=tanB=34，所以可以在△ABD 、△ADC 中反复地运用三角函数的定义和勾股定理来求解.解：根据题意，设AD=4k ，BD=3k ，则AB=5k.在Rt △ABC 中，∵tanB=34，∴AC=34AB=320k.∵BD=9,∴k=3. 所以AD=4×3=12，AC=320×3=20. 根据勾股定理25152022=+=BC .综合•应用7.已知α是锐角，且sinα=54，则cos(90°-α)=( )A.54B.43C.53D.51 思路解析：方法1.运用三角函数的定义，把α作为直角三角形的一个锐角看待，从而对边、邻边、斜边之比为4∶3∶5，(90°-α)是三角形中的另一个锐角，邻边与斜边之比为4∶5，cos(90°-α)=54.方法2.利用三角函数中互余角关系“sinα=cos(90°-α)”. 答案：A8.若α为锐角，tana=3，求ααααsin cos sin cos +-的值. 思路解析：方法1.运用正切函数的定义，把α作为直角三角形的一个锐角看待，从而直角三角形三边之比为3∶1∶10，sinα=103，cosα=101，分别代入所求式子中.方法2.利用tanα=ααcos sin 计算，因为cos α≠0，分子、分母同除以cosα，化简计算. 答案：原式=213131tan 1tan 1cos sin cos cos cos sin cos cos =+-=+-=+-αααααααααα. 9.已知方程x 2-5x·sinα+1=0的一个根为32+，且α为锐角，求tanα. 思路解析：由根与系数的关系可先求出方程的另一个根是32-，进而可求出sinα=54，然后利用前面介绍过的方法求tanα.解：设方程的另一个根为x 2，则(32+)x 2=1 ∴x 2=32-∴5sinα=(32+)+(32-)，解得sinα=54.设锐角α所在的直角三角形的对边为4k ，则斜边为5k ，邻边为3k ， ∴tanα=3434=k k . 10.同学们对公园的滑梯很熟悉吧！如图28.1-13是某公园(六·一)前新增设的一台滑梯，该滑梯高度AC=2 m ，滑梯着地点B 与梯架之间的距离BC=4 m.图28.1-13(1)求滑梯AB 的长(精确到0.1 m)；(2)若规定滑梯的倾斜角(∠ABC)不超过45°属于安全范围，请通过计算说明这架滑梯的倾斜角是否要求？思路解析：用勾股定理可以计算出AB 的长，其倾斜角∠ABC 可以用三角函数定义求出，看是否在45°范围内.解：(1)在Rt △ABC 中，2242+=AB ≈4.5. 答：滑梯的长约为4.5 m.(2)∵tanB=5.0=BCAC ,∴∠ABC≈27°, ∠ABC≈27°＜45°.所以这架滑梯的倾斜角符合要求. 11.四边形是不稳定的.如图28.1-14，一矩形的木架变形为平行四边形，当其面积变为原矩形的一半时，你能求出∠α的值吗？图28.1-14思路解析：面积的改变实际上是平行四边形的高在改变，结合图形，可以知道h=b 21，再在高所在的直角三角形中由三角函数求出α的度数.解：设原矩形边长分别为a ，b ，则面积为ab ， 由题意得，平行四边形的面积S=21ab.又因为S=ah=a(bsinα)，所以21ab=absinα，即sinα=21.所以α=30°.回顾•展望12.(2010海南模拟) 三角形在正方形网格纸中的位置如图28.3-15所示，则sinα的值是( )图28.1-15A.43B.34C.53D.54思路解析：观察格点中的直角三角形，用三角函数的定义. 答案：C13.(2010陕西模拟) 如图28.1-17，⊙O 是△ABC 的外接圆，AD 是⊙O的直径，连接CD ，若⊙O 的半径23 r ，AC=2，则cosB 的值是( )图28.1-17A.23B.35C.25D.32 思路解析：利用∠BCD=∠A 计算. 答案：D14.(浙江模拟) 在△ABC 中，∠C=90°，AB=15，sinA=31，则BC=( )A.45B.5C.51D.451 思路解析：根据定义sinA=ABBC ，BC=AB·sinA. 答案：B 15.(广西南宁课改模拟) 如图28.3-16，CD 是Rt △ABC 斜边上的高，AC=4，BC=3，则cos ∠BCD=( )图28.1-16A.53B.43C.34D.54思路解析：直径所对的圆周角是直角，设法把∠B 转移到Rt △ADC 中，由“同圆或等圆中，同弧或等弧所对的圆周角相等”，得到∠ADC=∠B. 答案：B16.(浙江舟山模拟) 课本中，是这样引入“锐角三角函数”的：如图28.1-18，在锐角α的终边OB 上，任意取两点P 和P 1，分别过点P和P 1做始边OA 的垂线PM 和P 1M 1，M 和M 1为垂足.我们规定，比值________叫做角α的正弦，比值________叫做角α的余弦.这是因为，由相似三角形的性质，可推得关于这些比值得两个等式：________，________.说明这些比值都是由________唯一确定的，而与P 点在角的终边上的位置无关，所以，这些比值都是自变量α的函数.图28.1-18思路解析：正弦、余弦函数的定义.答案：11111,,,OP OM OP OM OP M P OP PM OP OM OP PM ==，锐角α 17.(2010重庆模拟) 计算：2-1-tan60°+(5-1)0+|3|；思路解析：特殊角的三角函数，零指数次幂的意义，负指数次幂的意义. 解：2-1-tan60°+(5-1)0+|3|=21-3+1+3=23.18.(2010北京模拟) 已知：如图28.1-19，△ABC 内接于⊙O ，点D 在OC 的延长线上，sinB=21，∠CAD=30°.图28.1-19(1)求证：AD 是⊙O 的切线； (2)若OD ⊥AB ，BC=5，求AD 的长. 思路解析：圆的切线问题跟过切点的半径有关，连接OA ，证∠OAD=90°.由sinB=21可以得到∠B=30°，由此得到圆心角∠AOD=60°，从而得到△ACO 是等边三角形，由此∠OAD=90°.AD 是Rt △OAD 的边，有三角函数可以求出其长度.(1)证明：如图，连接OA.∵sinB=21，∴∠B=30°.∴∠AOD=60°.∵OA=OC ，∴△ACO 是等边三角形. ∴∠OAD=60°.∴∠OAD=90°.∴AD 是⊙O 的切线.(2)解：∵OD ⊥AB ∴ OC 垂直平分AB. ∴ AC=BC=5.∴OA=5. 在Rt △OAD 中，由正切定义，有tan ∠AOD=OA AD . ∴ AD=35.。

第1章解直角三角形 1.1 锐角三角函数（一）1.如图，在4×4的正方形网格中，小正方形的顶点称为格点，△ABC 的顶点都在格点上，则图中∠ABC 的余弦值是55.(第1题)2.已知sin α＝1213，则cos α＝513，tan α＝125.3.已知等腰三角形的面积为24，底边长为4，则底角的正切值为 6 .4.如图，若点A 的坐标为(1，3)，则sin ∠1＝(D)(第4题)A. 1B.3C.33 D. 325.在直角三角形中，若各边长都扩大到原来的2倍，则锐角A 的正弦值和余弦值都(C)A. 缩小到原来的12B. 扩大到原来的2倍C. 不变D. 不能确定(第6题)6.如图，在平面直角坐标系中，A 是第一象限内一点，直径为10的⊙A 经过点C(0，5)和点O(0，0)，点B 在y 轴右侧，且是⊙A 上一点，求∠OBC 的余弦值.【解】 作直径CD ，则点D 必在x 轴上. 在Rt △COD 中，∵CO ＝5，CD ＝10， ∴OD ＝CD 2－CO 2＝5 3.∴cos ∠OBC ＝cos ∠CDO ＝OD CD ＝5310＝32.(第7题)7.如图，直线y ＝12x －2交x 轴于点A ，交y 轴于点B ，且与x 轴的夹角为α，求：(1)OA ，OB 的长. (2)tan α与sin α的值.【解】 (1)令y ＝0，则x ＝4， ∴点A(4，0)，∴OA ＝4. 令x ＝0，则y ＝－2， ∴点B(0，－2)，∴OB ＝2.(2)在Rt △AOB 中，OB ＝2，OA ＝4， ∴AB ＝OB 2＋OA 2＝25， ∴tan α＝tan ∠OAB ＝OB OA ＝12，sin α＝sin ∠OAB ＝OB AB ＝225＝55.(第8题)8.如图，在Rt △ABC 中，已知∠C ＝90°，AC ＝BC ＝6，D 是AC 上一点，tan ∠DBA ＝15，求AD 的长. 【解】 过点D 作DE ⊥AB 于点E. ∵∠C ＝90°，AC ＝BC ＝6，∴△ACB 为等腰直角三角形，AB ＝2AC ＝6 2，∴∠A ＝45°.设AE ＝x ，则DE ＝x ，AD ＝2x. 在Rt △BED 中，∵tan ∠DBE ＝DEBE ，∴BE ＝DEtan ∠DBE ＝5x ，∴x ＋5x ＝62，解得x ＝ 2.∴AD ＝2x ＝2.9.如图，折叠矩形ABCD 的一边AD ，使点D 落在BC 边上的点F 处.已知折痕AE ＝55cm ，且tan ∠EFC ＝34，则矩形ABCD 的周长为 36 cm.(第9题)【解】 ∵tan ∠EFC ＝34，∴可设CE ＝3k ，CF ＝4k ， ∴由勾股定理，得DE ＝EF ＝5k ， ∴AB ＝DC ＝8k.∵∠AFB ＋∠BAF ＝90°，∠AFB ＋∠EFC ＝90°， ∴∠BAF ＝∠EFC ，∴tan ∠BAF ＝tan ∠EFC ＝34，∴BF ＝6k ，BC ＝AD ＝AF ＝10k.在Rt△AFE中，由勾股定理，得AE＝AF2＋EF2＝125 k2＝5 5，解得k＝1.∴矩形ABCD的周长＝2(AB＋BC)＝2(8＋10)＝36(cm).10.在△ABC中，∠C＝90°，△ABC的面积为6，斜边长为6，则tan A＋tan B的值为 3 .【解】∵△ABC的面积为6，∴BC·AC＝12.在Rt△ABC中，∵∠C＝90°，AB＝6，∴BC2＋AC2＝62＝36，∴tan A＋tan B＝BCAC＋ACBC＝BC2＋AC2AC·BC＝3612＝3.11.如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连结DF.有下列结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝ 2.其中正确的结论有(B)A. 4个B. 3个C. 2个D. 1个(第11题)【解】如解图，过点D作DM∥BE交AC于点N.(第11题解)∵四边形ABCD是矩形，∴AD ∥BC ，∠ABC ＝90°，AD ＝BC ， ∴∠EAC ＝∠ACB. ∵BE ⊥AC 于点F ， ∴∠EFA ＝∠ABC ＝90°， ∴△AEF ∽△CAB ，故①正确. ∵AD ∥BC ，∴△AEF ∽△CBF ， ∴AE CB ＝AF CF. ∵E 是AD 边的中点，∴AE ＝12AD ＝12BC ，∴AF CF ＝12，∴CF ＝2AF ，故②正确. ∵DE ∥BM ，BE ∥DM ， ∴四边形BMDE 是平行四边形， ∴BM ＝DE ＝12BC ，∴BM ＝CM ，∴CN ＝NF ， ∴DN 垂直平分FC ， ∴DF ＝DC ，故③正确. 设AD ＝a ，AB ＝b.易得△BAE ∽△ADC ，∴BA AD ＝AE DC ，即b a ＝a2b ，∴2b 2＝a 2.∵tan ∠CAD ＝CD AD ＝ba，∴tan ∠CAD ＝22，故④错误.综上所述，正确的结论有3个.12.如图，在Rt △AOB 中，两直角边OA ，OB 分别在x 轴的负半轴和y 轴的正半轴上，将△AOB 绕点B 逆时针旋转90°后得到△A ′O ′B.若反比例函数y ＝kx 的图象恰好经过斜边A ′B 的中点C ，S △ABO ＝4，tan ∠BAO ＝2，求k 的值.(第12题)【解】 如解图，过点C 作CD ⊥BO ′于点D ，设点C 的坐标为(x ，y).(第12题解)∵tan ∠BAO ＝2，∴BOAO＝2. 又∵S △ABO ＝12AO ·BO ＝4，∴AO ＝2，BO ＝4.∴A ′O ′＝AO ＝2，BO ′＝BO ＝4.∵C 为Rt △A ′O ′B 斜边A ′B 的中点，CD ⊥BO ′， ∴CD ＝12A ′O ′＝1，BD ＝12BO ′＝2，∴y ＝BO －CD ＝4－1＝3，x ＝BD ＝2， ∴k ＝x ·y ＝6.(第13题)13.如图，AB 是⊙O 的直径，CD 是弦，CD ⊥AB 于点E ，连结AC ，BC ，BD. (1)求证：△ACE ∽△CBE.(2)若AB ＝8，设OE ＝x(0<x<4)，CE 2＝y ，请求出y 关于x 的函数表达式. (3)探究：当x 为何值时，tanD ＝33？【解】 (1)∵AB 为⊙O 的直径， ∴∠ACB ＝90°，即∠ACE ＋∠BCE ＝90°. ∵CD ⊥AB ，∴∠AEC ＝∠CEB ＝90°，∠A ＋∠ACE ＝90°， ∴∠A ＝∠BCE ，∴△ACE ∽△CBE. (2)∵△ACE ∽△CBE ，∴AE CE ＝CEBE ，即CE 2＝AE ·BE ＝(AO ＋OE)(OB －OE). ∴y ＝(4＋x)(4－x)＝16－x 2. (3)∵tanD ＝33，即tanA ＝33，∴CE AE ＝33，则CE 2AE 2＝13，即16－x 2（4＋x ）2＝13，解得x 1＝2，x 2＝－4(舍去).故当x ＝2时，tanD ＝33.14.通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.类似地，可以在等腰三角形中建立边角之间的联系.我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①，在△ABC 中，AB ＝AC ，顶角A 的正对记做sadA ，这时sadA ＝底边腰＝BC AB .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对的定义，解答下列问题：(1)sad60°＝ 1 .(2)对于0°<∠A<180°，∠A 的正对值sadA 的取值范围是0<∠sadA<2 . (3)如图②，已知sinA ＝35，其中∠A 为锐角，试求sadA 的值.（第14题）(第14题解)【解】 (3)设AB ＝5a ，则BC ＝3a ，AC ＝4a.如解图，在AB 上取AD ＝AC ＝4a ，过点D 作DE ⊥AC 于点E ，连结CD ，则DE ＝AD ·sinA ＝4a ·35＝125a ，AE ＝AD ·cosA ＝4a ·45＝165a ，CE ＝4a －165a ＝45a. ∴CD ＝CE 2＋DE 2＝⎝ ⎛⎭⎪⎫45a 2＋⎝ ⎛⎭⎪⎫125a 2 ＝4105a. ∴sadA ＝CD AC ＝105.。

2021-2022学年北师大版数学九年级下册压轴题专题精选汇编专题01 锐角三角函数一．选择题1．（2021春•金台区期末）如图，在Rt△ABC中∠C＝90°，直线MN垂直平分AB交AB于M，交BC于N，且∠B＝15°，AC＝3，则BC的长为（ ）A．6B．6+3C．6+2D．9【思路引导】如图，连接AN．证明AN＝BN，推出∠B＝∠NAB＝15°，推出∠ANC＝30°，再求出AN，CN，可得结论．【完整解答】如图，连接AN．∵MN垂直平分线段AB，∴NA＝NB，∴∠B＝∠BAN＝15°，∴∠ANC＝∠B+∠NAB＝30°，∵AC＝3，∠C＝90°，∴AN＝2AC＝6，CN＝＝＝3，∴BC＝CN+BN＝3+6，故选：B．2．（2020秋•南召县期末）如图，在4×5的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的格点上，那么tan∠ABC的值为（ ）A．B．C．4D．【思路引导】过点A作AE⊥BC于E．根据，tan∠ABC＝，求解即可．【完整解答】过点A作AE⊥BC于E．在Rt△ABE中，tan∠ABC＝＝＝4，故选：C．3．（2020秋•仁寿县期末）等腰三角形底边与底边上的高的比是2：，则它的顶角为（ ）A．30°B．45°C．60°D．120°【思路引导】证明△ABC是等边三角形，可得结论．【完整解答】如图，AB＝AC，AD⊥BC，∴BD＝CD，∵BC：AD＝2：，∴tan B＝＝，∴∠B＝60°，∵AB＝AC，∴△ABC是等边三角形，∴∠BAC＝60°，故选：C．4．（2020秋•紫金县期末）如图，点A（3，4）在第一象限，OA与x轴所夹的锐角为α，则cosα＝（ ）A．B．C．D．【思路引导】过点A作AE⊥x轴于E．利用勾股定理求出OA，再根据cosα＝，可得结论．【完整解答】如图，过点A作AE⊥x轴于E．∵A（3，4），∴OE＝3，AE＝4，∴OA＝＝＝5，∴cosα＝＝，故选：B．5．（2021•淄博）如图，在Rt△ABC中，∠ACB＝90°，CE是斜边AB上的中线，过点E作EF⊥AB交AC 于点F．若BC＝4，△AEF的面积为5，则sin∠CEF的值为（ ）A．B．C．D．【思路引导】根据直角三角形的斜边中线等于斜边一半可得CE ＝AE ＝BE ＝AB ，进而得到∠BEC ＝2∠A ＝∠BFC ，从而有∠CEF ＝∠CBF ，根据三角形的面积公式求出AF ，由勾股定理，在Rt △BCF 中，求出CF ，再根据锐角三角函数的定义求解即可．【完整解答】连接BF ，∵CE 是斜边AB 上的中线，EF ⊥AB ，∴EF 是AB 的垂直平分线，∴S △AFE ＝S △BFE ＝5，∠FBA ＝∠A ，∴S △AFB ＝10＝AF •BC ，∵BC ＝4，∴AF ＝5＝BF ，在Rt △BCF 中，BC ＝4，BF ＝5，∴CF ＝＝3，∵CE ＝AE ＝BE ＝AB ，∴∠A ＝∠FBA ＝∠ACE ，又∵∠BCA ＝90°＝∠BEF ，∴∠CBF ＝90°﹣∠BFC ＝90°﹣2∠A ，∠CEF ＝90°﹣∠BEC ＝90°﹣2∠A ，∴∠CEF ＝∠FBC ，∴sin ∠CEF ＝sin ∠FBC ＝＝，故选：A ．6．（2021•宜兴市模拟）如图，在△ABC 中，∠ABC ＝90°，tan ∠BAC ＝，AD ＝2，BD ＝4，连接CD ，则CD 长的最大值是（ ）A ．2+B ．2+1C ．2+D ．2+2【思路引导】如图，在AD 的下方作Rt △ADT ，使得∠ADT ＝90°，DT ＝1，连接CT ，则AT ＝，证明△DAB ∽△TAC ，推出＝＝，推出TC ＝2，再根据CD ≤DT +CT ，可得CD ≤1+2，由此即可解决问题．【完整解答】如图，在AD 的下方作Rt △ADT ，使得∠ADT ＝90°，DT ＝1，连接CT ，则AT ＝，∵＝＝2，∴＝，∵∠ADT ＝∠ABC ＝90°，∴△ADT ∽△ABC ，∴∠DAT ＝∠BAC ，＝∴∠DAB ＝∠TAC ，∵＝，∴△DAB ∽△TAC ，∴＝＝，∴TC ＝2，∵CD≤DT+CT，∴CD≤1+2，∴CD的最大值为1+2，故选：B．7．（2020秋•北碚区校级期末）北碚区政府计划在缙云山半山腰建立一个基站AB，其设计图如图所示，BF，ED与地面平行，CD的坡度为i＝1：0.75，EF的坡角为45°，小王想利用所学知识测量基站顶部A 到地面的距离，若BF＝ED，CD＝15米，EF＝3米，小王在山脚C点处测得基站底部B的仰角为37°，在F点处测得基站顶部A的仰角为60°，则基站顶部A到地面的距离为（ ）（精确到0.1米，参考数据：≈1.73，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）A．21.5米B．21.9米C．22.0米D．23.9米【思路引导】延长AB交过点C的水平线于M，交DE延长线于点N，作DG⊥MC于G，FH⊥DN于H，根据锐角三角函数即可求出结果．【完整解答】如图，延长AB交过点C的水平线于M，交DE延长线于点N，作DG⊥MC于G，FH⊥DN于H，∵CD的坡度为i＝1：0.75＝，∴＝，设DG＝4k，CG＝3k，则CD＝5k，∴5k＝15，∴k＝3，∴DG＝12，CG＝9，∵EF的坡角为45°，EF＝3，∴EH＝FH＝3，∵四边形BNHF和四边形DGMN是矩形，∴BF＝NH＝DE，BN＝FH＝3，DN＝MG，NM＝DG＝12，∴BM＝BN+NM＝15，在Rt△BCM中，∠BCM＝37°，MC＝MG+CG＝DN+CG＝NH+HE+DE+CG＝2BF+3+9＝2BF+12，∴BM＝CM•tan∠BCM，∴15＝（2BF+12）×0.75，∴BF＝4，在Rt△ABF中，∠AFB＝60°，∴AB＝BF•tan60°＝4≈6.92（米），∴AM＝AB+BM＝6.92+15≈21.9（米）．故选：B．8．（2021•渝中区校级二模）如图，旗杆AB竖立在斜坡CB的顶端，斜坡CB长为65米，坡度为i＝．小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E，在此测得旗杆顶端点A的仰角为39°，则旗杆的高度AB约为（ ）米．（参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）A．12.9B．22.2C．24.9D．63.1【思路引导】通过作高，构造直角三角形，利用直角三角形的边角关系和坡度即可求出答案．【完整解答】过点B作BF⊥CD，垂足为F，过点E作EG⊥BF，垂足为G，在Rt△BCF中，由斜坡BC的坡度i＝，得，＝，又BC＝65，设BF＝12x，FC＝5x，由勾股定理得，（12x）2+（5x）2＝652，∴x＝5，∴BF＝60，FC＝25，又∵DC＝115，∴DF＝DC﹣FC＝115﹣25＝90＝EG，在Rt△AEG中，AG＝EG•tan39°≈90×0.81＝72.9，∴AB＝AG+FG﹣BF＝72.9+12﹣60＝24.9（米），故选：C．二．填空题（共11小题）9．（2021春•沙河口区期末）如图，从一艘船A上测得海岸上高为42米的灯塔顶部B的仰角∠BAC＝30°，求船离灯塔的水平距离AC的长度是　71　米（参考数据：≈1.7，≈2.2，结果取整数）．【思路引导】由含30°角的直角三角形的性质得AB＝2BC＝84（米），再由勾股定理即可求解．【完整解答】由题意得：∠ACB＝90°，∠BAC＝30°，BC＝42米，∴AB＝2BC＝84（米），∴AC＝＝＝42≈71（米），故答案为：71．10．（2020秋•肥城市期末）如图，在正方形网格中，△ABC的顶点都在格点上，则cos B+sin B的值为　　．【思路引导】如图，过点A作AE⊥BC交BC的延长线于E．利用勾股定理求出AB，可得结论．【完整解答】如图，过点A作AE⊥BC交BC的延长线于E．在Rt△ABE中，∠E＝90°，AE＝3，BE＝4，∴AB＝＝＝5，∴cos B＝＝，sin B＝＝，∴cos B+sin A＝+＝，故答案为：．11．（2020秋•崇川区期末）如图，若A，B，C，D都在格点处，AB与CD相交于O，则∠BOD的余弦值为 ．【思路引导】如图，取格点T，连接CT．DT．利用平行线的性质证明∠BOD＝∠TCD，求出CT，CD，可得结论．【完整解答】如图，取格点T，连接CT．DT．观察图象可知，CT∥AB，CT⊥DT，∴∠BOD＝∠TCD，∠CTD＝90°，∵CT＝＝，CD＝＝5，∴cos∠BDO＝cos∠TCD＝＝＝，故答案为：．12．（2020秋•锡山区期末）如图的正方形网格中，△ABC的顶点都在格点上，则tan∠ACB的值为　　．【思路引导】如图，过点A作AH⊥BC于H．利用面积法求出AH，再利用勾股定理求出BH，CH，可得结论．【完整解答】如图，过点A作AH⊥BC于H．∵AB＝2，BC＝5，＝×2×4＝•BC•AH，∴S△ABC∴AH＝，∴BH＝＝＝，∴CH＝BC﹣BH＝5﹣＝，∴tan∠ACB＝＝＝，故答案为：．13．（2020秋•龙口市期末）如图，在Rt△ABC中，∠C＝90°，D为边AC上一点，∠A＝∠CBD，若AC＝8cm，cos∠CBD＝，则边AB＝　10　cm．【思路引导】根据锐角三角函数即可求出AB的值．【完整解答】∵∠C＝90°，∠A＝∠CBD，cos∠CBD＝，∴cos∠A＝＝，∵AC＝8cm，∴AB＝10cm．故答案为：10．14．（2020秋•德江县期末）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F，若AC＝6，tan B＝，则CE＝　3　．【思路引导】过点F作FG⊥AB于点G，根据三角形的内角和定理得出∠CAF+∠CFA＝90°，∠FAD+∠AED＝90°，根据角平分线和对顶角相等得出∠CEF＝∠CFE，即可得出EC＝FC，再利用相似三角形的判定与性质得出答案．【完整解答】过点F作FG⊥AB于点G，∵∠ACB＝90°，CD⊥AB，∴∠CDA＝90°，∴∠CAF+∠CFA＝90°，∠FAD+∠AED＝90°，∵AF平分∠CAB，∴∠CAF＝∠FAD，∴∠CFA＝∠AED＝∠CEF，∴CE＝CF，∵AF平分∠CAB，∠ACF＝∠AGF＝90°，∴FC＝FG，∵∠B＝∠B，∠FGB＝∠ACB＝90°，∴△BFG∽△BAC，∴＝，∵AC＝6，∠ACB＝90°，∴tan B＝＝∴BC＝8，AB＝＝＝10，∴＝，∵FC＝FG，解得：FC＝3，即CE的长为3．故答案为：3．15．（2020秋•新吴区期末）如图，△ABC的顶点都在正方形网格纸的格点上，则sin＝ ．【思路引导】如图，取格点T，连接AT，BT，设BT的中点为H，连接CH．证明CB＝CT，利用等腰三角形的性质求解即可．【完整解答】如图，取格点T，连接AT，BT，设BT的中点为H，连接CH．∵BC＝＝5，CT＝＝5，∴CB＝CT，∵BH＝HT，∴∠HCA＝∠HCB，CH⊥BT，∵HT＝，∴sin＝＝＝，故答案为：．16．（2021春•瑞安市月考）如图，在河对岸有一等腰三角形场地EFG，FG＝EG，为了估测场地的大小，在笔直的河岸上依次取点C，D，B，A，使FC⊥l，BG⊥l，EA⊥l，点E，G，D在同一直线上，在D观测F后，发现∠FDC＝∠EDA，测得CD＝12米，DB＝6米，AB＝12米，则FG＝　8　米．【思路引导】过点G作GM⊥AE于G．GN⊥EF于N，过点D作DJ⊥l，过点F作FT⊥AE于T．利用相似三角形的性质证明DF＝FG，再证明∠DEA＝∠DEF，推出EN＝EM＝FN，证明△EGM≌△EGN （AAS），推出EM＝EN，设AM＝m，在Rt△ETF中，利用勾股定理求出方程求出m，即可解决问题．【完整解答】过点G作GM⊥AE于G．GN⊥EF于N，过点D作DJ⊥l，过点F作FT⊥AE于T．∵FC⊥l，BG⊥l，EA⊥l，∴∠FCD＝∠EAD＝90°，BG∥AE，∵∠FDC＝∠EDA，∴△FCD∽△EAD，△GBD∽EAD，∴＝＝2，＝＝，∴DF＝2DG，DE＝3DG，∴EG＝FG＝2DG，∴FD＝FG，∴∠FDG＝∠FGD＝∠GFE+∠GEF，∵GE＝GF，∴∠GEF＝∠GFE，∵∠FDJ+∠FDC＝90°，∠EDJ+∠EDA＝90°，∠FDC＝∠EDA，∴∠FDJ＝∠EDJ，∴2∠EDJ＝2∠GEF，∴∠EDJ＝∠DEF，∵DJ∥AE，∴∠EDJ＝∠AED，∴∠DEA＝∠DEF，∵GM⊥AE，GN⊥EF，∴∠EMG＝∠ENG＝90°，∵EG＝EG，∴△EGM≌△EGN（AAS），∴EM＝EN，∵GE＝GF，GN⊥EF，∴FN＝EN＝EM，∵四边形ABGM，四边形CFTA都是矩形，∴AB＝GM＝CD＝6（米），∵DF＝EG，∠FCD＝∠GME＝90°，∴Rt△FCD≌Rt△EMG（HL），∴CF＝EM，设AM＝m米则AE＝3m米，EM＝CF＝AT＝FN＝EN＝2m米，∴ET＝AE﹣AT＝m（米），在Rt△EFT中，FT2+ET2＝EF2，∴302+m2＝（4m）2，∴m＝2或﹣2（舍弃），∴FN＝4（米），∵GN＝GM＝12米，∴FG＝＝＝8（米），故答案为：8．17．（2021•道里区三模）△ABC中，AB＝8，∠B＝60°，AC＝7，则∠BAC的余弦值为　或　．【思路引导】分两种情况进行解答，即当△ABC是锐角三角形和△ABC是钝角三角形，分别画出相应的图形，通过做高，利用直角三角形的边角过程求出相应的边长，再根据锐角三角函数的意义求出答案．【完整解答】（1）如图1，过点A作AD⊥BC，垂足为D，过点C作CE⊥AC，垂足为E，在Rt△ABD中，∠ABD＝60°，AB＝8，∴BD＝AB＝4，AD＝AB＝4，在Rt△ACD中，CD＝＝1，由三角形的面积公式得，BC•AD＝AC•BE，即（4+1）×4＝7BE，∴BE＝，在Rt△ABE中，AE＝＝，∴cos∠BAC＝＝＝；（2）如图2，过点A作AD⊥BC，垂足为D，过点C作CF⊥AB，垂足为F，由题意得，BC＝4﹣1＝3，在Rt△BCF中，∠FBC＝60°，BC＝3，∴BF＝BC＝，∴AF＝AB﹣FB＝8﹣＝，在Rt△AFC中，cos∠BAC＝＝；故答案为：或．18．（2021•新洲区模拟）如图，在Rt△ABC中，∠ACB＝90°，AC＝10，BC＝5，M是射线AB上的一动点，以AM为斜边在△ABC外作Rt△AMN，且使tan∠MAN＝，O是BM的中点，连接ON．则ON长的最小值为　2　．【思路引导】作NP⊥AB于点P，设AM长为x，用含x代数式表示出ON，然后通过配方求解．【完整解答】作NP⊥AB于点P，在Rt△ACB中，由勾股定理得：AB＝＝＝5，设AM长为x，则BM＝5﹣x，∵tan∠MAN＝＝，∴AN＝2MN，∴AM＝＝MN，∴MN＝AM＝x，AN＝2MN＝x，同理，在Rt△ANP中可得NP＝＝x，AP＝2NP＝x，∵O为BM中点，∴BO＝BM＝，∴AO＝AB﹣BO＝，∴OP＝AO﹣AP＝﹣x＝，在Rt△ONP中，由勾股定理得ON2＝OP2+NP2，即ON2＝（）2+（x）2＝（25x2﹣150x+3125）＝（x2﹣6x+125）＝（x﹣3）2+20，∴当x＝3时，ON2取最小值为20，∴ON最小值为2．故答案为：2．19．（2021•乐山）如图，已知点A（4，3），点B为直线y＝﹣2上的一动点，点C（0，n），﹣2＜n＜3，AC⊥BC于点C，连接AB．若直线AB与x正半轴所夹的锐角为α，那么当sinα的值最大时，n的值为 ．【思路引导】当sinα的值最大时，则tanα＝值最大，即当BG最大时，sinα的值最大，设BG＝y，由tan∠CAM＝tan∠BCG，得到y＝﹣（n﹣3）（n+2），进而求解．【完整解答】过点A作AM⊥y轴于点M，作AN⊥BN交于点N，∵直线y＝﹣2∥x轴，故∠ABN＝α，当sinα的值最大时，则tanα＝值最大，故BN最小，即BG最大时，tanα最大，即当BG最大时，sinα的值最大，设BG＝y，则AM＝4，GC＝n+2，CM＝3﹣n，∵∠ACM+∠MAC＝90°，∠ACM+∠BCG＝90°，∴∠CAM＝∠BCG，∴tan∠CAM＝tan∠BCG，∴，即，∴y＝﹣（n﹣3）（n+2），∵﹣＜0，故当n＝（3﹣2）＝时，y取得最大值，故n＝，故答案为：．三．解答题20．（2021•河池）如图，小明同学在民族广场A处放风筝，风筝位于B处，风筝线AB长为100m，从A处看风筝的仰角为30°，小明的父母从C处看风筝的仰角为50°．（1）风筝离地面多少m？（2）A、C相距多少m？（结果保留小数点后一位，参考数据：sin30°＝0.5，cos30°≈0.8660，tan30°≈0.5774，sin50°≈0.7760，cos50°≈0.6428，tan50°≈1.1918）【思路引导】（1）过B作BD⊥AC于D，由含30°角的直角三角形的性质即可求解；（2）由锐角三角函数定义求出CD、AD的长，即可求解．【完整解答】（1）过B作BD⊥AC于D，如图所示：则∠ADB＝∠CDB＝90°，∵∠BAD＝30°，∴BD＝AB＝50（m），即风筝离地面50m；（2）由（1）得：BD＝50m，在Rt△BCD中，∠BCD＝50°，∵tan∠BCD＝＝tan50°≈1.1918，∴CD≈＝≈41.95（m），在Rt△ABD中，∠BAD＝30°，∵tan∠BAD＝＝tan30°≈0.5774，∴AD≈≈86.60（m），∴AC＝AD+CD≈41.95+86.60≈128.6（m），即A、C相距约128.6m．21．（2020秋•长沙期末）如图，A、B、D三点在同一水平线上，CD⊥AD，∠A＝45°，∠CBD＝75°，AB＝60m．（1）求∠ACB的度数；（2）求线段CB的长度．【思路引导】（1）利用三角形的外角的性质求解即可．（2）如图，过点B作BH⊥AC于H，利用等腰直角三角形的性质求出BH，再根据BC＝2BH，可得结论．【完整解答】（1）∵∠CBD＝∠A+∠ACB，∠A＝45°，∠CBD＝75°，∠∠ACB＝75°﹣45°＝30°．（2）如图，过点B作BH⊥AC于H．∵∠BHA＝90°，AB＝60m，∠A＝45°，∴BH＝AB•sin45°＝60（m），∵∠BCH＝30°，∴BC＝2BH＝120（m）．22．（2021•朝阳）一数学兴趣小组去测量一棵周围有围栏保护的古树的高，在G处放置一个小平面镜，当一位同学站在F点时，恰好在小平面镜内看到这棵古树的顶端A的像，此时测得FG＝3m，这位同学向古树方向前进了9m后到达点D，在D处安置一高度为1m的测角仪CD，此时测得树顶A的仰角为30°，已知这位同学的眼睛与地面的距离EF＝1.5m，点B，D，G，F在同一水平直线上，且AB，CD，EF均垂直于BF，求这棵古树AB的高．（小平面镜的大小和厚度忽略不计，结果保留根号）【思路引导】过点C作CH⊥AB于点H，则CH＝BD，BH＝CD＝1m，由锐角三角函数定义求出BD＝CH＝AH，再证△EFG∽△ABG，得＝，求出AH＝（8+4）m，即可求解．【完整解答】如图，过点C作CH⊥AB于点H，则CH＝BD，BH＝CD＝1m，由题意得：DF＝9m，∴DG＝DF﹣FG＝6（m），在Rt△ACH中，∠ACH＝30°，∵tan∠ACH＝＝tan30°＝，∴BD＝CH＝AH，∵EF⊥FB，AB⊥FB，∴∠EFG＝∠ABG＝90°．由反射角等于入射角得∠EGF＝∠AGB，∴△EFG∽△ABG，∴＝，即＝，解得：AH＝（8+4）m，∴AB＝AH+BH＝（9+4）m，即这棵古树的高AB为（9+4）m．23．（2021•锦州）如图，山坡上有一棵竖直的树AB，坡面上点D处放置高度为1.6m的测倾器CD，测倾器的顶部C与树底部B恰好在同一水平线上（即BC∥MN），此时测得树顶部A的仰角为50°．已知山坡的坡度i＝1：3（即坡面上点B处的铅直高度BN与水平宽度MN的比），求树AB的高度（结果精确到0.1m．参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）【思路引导】先求出BC＝4.8m，再由锐角三角函数定义即可求解．【完整解答】∵山坡BM的坡度i＝1：3，∴i＝1：3＝tan M，∵BC∥MN，∴∠CBD＝∠M，∴tan∠CBD＝＝tan M＝1：3，∴BC＝3CD＝4.8（m），在Rt△ABC中，tan∠ACB＝＝tan50°≈1.19，∴AB≈1.19BC＝1.19×4.8≈5.7（m），即树AB的高度约为5.7m．24．（2020秋•阜宁县期末）在Rt△ABC中，∠C＝90°，∠A﹣∠B＝30°，a﹣b＝2﹣2，解这个直角三角形．【思路引导】利用三角形内角和定理构建方程组求出∠A，∠B的值，推出a＝b，解方程组求出a，b，即可解决问题．【完整解答】∵，∴，∵，∴，由，解得，∵，∴c＝2b＝4．25．（2021•荆门）某海域有一小岛P，在以P为圆心，半径r为10（3+）海里的圆形海域内有暗礁．一海监船自西向东航行，它在A处测得小岛P位于北偏东60°的方向上，当海监船行驶20海里后到达B处，此时观测小岛P位于B处北偏东45°方向上．（1）求A，P之间的距离AP；（2）若海监船由B处继续向东航行是否有触礁危险？请说明理由．如果有触礁危险，那么海监船由B 处开始沿南偏东至多多少度的方向航行能安全通过这一海域？【思路引导】（1）通过作垂线构造直角三角形，求出小岛P到航线AB的最低距离PC，与暗礁的半径比较即可得出答案；（2）规划新航线BD，使小岛P到新航线的距离PE等于暗礁的半径，进而求出∠PBD，进而求出∠CBD，确定方向角．【完整解答】（1）过点P作PC⊥AB，交AB的延长线于点C，由题意得，∠PAC＝30°，∠PBC＝45°，AB＝20，设PC＝x，则BC＝x，在Rt△PAC中，∵tan30°＝＝＝，∴x＝10+10，∴PA＝2x＝20+20，答：A，P之间的距离AP为（20+20）海里；（2）因为PC﹣10（3+）＝10+10﹣30﹣10＝10（+1）（﹣）＜0，所以有触礁的危险；设海监船无触礁危险的新航线为射线BD，作PE⊥BD，垂足为E，当P到BD的距离PE＝10（3+）海里时，有sin∠PBE＝＝＝，∴∠PBD＝60°，∴∠CBD＝60°﹣45°＝15°，90°﹣15°＝75°即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域．26．（2021•天津）如图，一艘货船在灯塔C的正南方向，距离灯塔257海里的A处遇险，发出求救信号．一艘救生船位于灯塔C的南偏东40°方向上，同时位于A处的北偏东60°方向上的B处，救生船接到求救信号后，立即前往救援．求AB的长．（结果取整数）参考数据：tan40°≈0.84，取1.73．【思路引导】通过作垂线，构造直角三角形，利用锐角三角函数的意义列方程求解即可．【完整解答】如图，过点B作BH⊥AC，垂足为H，由题意得，∠BAC＝60°，∠BCA＝40°，AC＝257海里，在Rt△ABH中，∵tan∠BAH＝，cos∠BAH＝，∴BH＝AH•tan60°＝AH，AB＝＝2AH，在Rt△BCH中，∵tan∠BCH＝，∴CH＝＝（海里），又∵CA＝CH+AH，∴257＝+AH，所以AH＝（海里），∴AB＝≈＝168（海里），答：AB的长约为168海里．27．（2021•资阳）资阳市为实现5G网络全覆盖，2020﹣2025年拟建设5G基站七千个．如图，在坡度为i＝1：2.4的斜坡CB上有一建成的基站塔AB，小芮在坡脚C测得塔顶A的仰角为45°，然后她沿坡面CB 行走13米到达D处，在D处测得塔顶A的仰角为53°．（点A、B、C、D均在同一平面内）（参考数据：sin53°≈，cos53°≈，tan53°≈）（1）求D处的竖直高度；（2）求基站塔AB的高．【思路引导】（1）通过作垂线，利用斜坡CB的坡度为i＝1：2.4，CD＝13，由勾股定理可求出答案；（2）设出DE的长，根据坡度表示BE，进而表示出CF，由于△ACF是等腰直角三角形，可表示BE，在△ADE中由锐角三角函数可列方程求出DE，进而求出AB．【完整解答】（1）如图，过点C、D分别作AB的垂线，交AB的延长线于点E、F，过点D作DM⊥CF，垂足为M，∵斜坡CB的坡度为i＝1：2.4，∴＝，即＝，设DM＝5k米，则CM＝12k米，在Rt△CDM中，CD＝13米，由勾股定理得，CM2+DM2＝CD2，即（5k）2+（12k）2＝132，解得k＝1，∴DM＝5（米），CM＝12（米），答：D处的竖直高度为5米；（2）斜坡CB的坡度为i＝1：2.4，设DE＝12a米，则BE＝5a米，又∵∠ACF＝45°，∴AF＝CF＝（12+12a）米，∴AE＝AF﹣EF＝12+12a﹣5＝（7+12a）米，在Rt△ADE中，DE＝12a米，AE＝（7+12a）米，∵tan∠ADE＝tan53°≈，∴＝，解得a＝，∴DE＝12a＝21（米），AE＝7+12a＝28（米），BE＝5a＝（米），∴AB＝AE﹣BE＝28﹣＝（米），答：基站塔AB的高为米．28．（2021•莱芜区二模）如图，为加强对市内道路交通安全的监督，王警官利用无人机进行检测．某段限速道路AB＝328米，当无人机在限速道路的正上方C处时，测得限速道路的起点A的俯角是37°，无人机继续向右水平飞行到达D处，此时又测得起点A的俯角是30°，同时测得限速道路终点B的俯角是45°．求无人机距离地面道路的高度和飞行距离各为多少米．（均精确到1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，≈1.73）【思路引导】通过作垂线构造直角三角形，在不同的直角三角形中，利用边角关系进行计算即可．【完整解答】（1）如图，由题意得：∠ECA＝37°，∠CDA＝30°，∠FDB＝45°，CD∥AB，AB＝328米，过点C作CM⊥AB于点M，过点D作DN⊥AB于点N，则四边形CDNM是矩形，∵∠ECA＝37°，∠CDA＝30°，∠FDB＝45°，CD∥AB，∴∠CAM＝∠ECA＝37°，∠DAN＝∠CDA＝30°，∠B＝∠FDB＝45°，即无人机距离地面道路的高度为120米，∴，∴CD＝MN＝AN﹣AM＝207.6﹣160≈48米，即无人机的飞行距离为48米．29．（2021•碑林区校级模拟）学校“科技创新小团队”设计的智能照明家居（如图①）的设计方案（如图②）所示：MN为台灯底座，支架AB与MN的夹角为60°．支架AB与BC的夹角可以调节的．试用后发现，当支架AB与BC的夹角为108°时，可以达到较好的照明效果．若AB＝21cm，BC＝28cm．此时点C离底座MN的距离为多少？（结果精确到0.1cm．参考数据：≈1.41；≈1.73；sin48°≈0.74；cos48°≈0.67；tan48°≈1.11）【思路引导】过点C作CE⊥MN于点M，过点B作BF⊥MN于点F，作BG⊥CE于点G，得矩形EGBF，根据锐角三角函数即可求出CG和BF的值，进而可得结果．【完整解答】如图，过点C作CE⊥MN于点M，过点B作BF⊥MN于点F，作BG⊥CE于点G，得矩形EGBF，在Rt△ABF中，∵∠BAF＝60°，AB＝21cm，∴∠ABF＝30°，∴AF＝AB＝cm，∴BF＝AF＝≈18.165（cm），∴GE＝BF≈18.165（cm），在Rt△CGB中，∵∠CBG＝108°﹣60°＝48°，BC＝28cm．∴CG＝BC×sin48°≈28×0.74≈20.72（cm），∴CE＝CG+GE＝20.72+18.165≈38.9（cm），答：此时点C离底座MN的距离为38.9cm．。

九年级下《锐角三角函数》专项训练含答案专训 1求锐角三角函数值的常用方法名师点金：锐角三角函数刻画了直角三角形中边和角之间的关系，对于斜三角形，要把它转化为直角三角形求解．在求锐角的三角函数值时，首先要明确是求锐角的正弦值，余弦值还是正切值，其次要弄清是哪两条边的比．直接用锐角三角函数的定义1．如图，在Rt△ABC中，CD是斜边AB上的中线，若CD＝5，AC＝6，(第 1 题)则 tan B 的值是 ()43A.5B.534C.4D.32．如图，在△ABC中，AD⊥BC，垂足是D，若BC＝14，AD＝12，tan∠3BAD ＝4，求 sin C 的值．(第 2 题)133．如图，直线y＝2x＋2与x轴交于点A，与直线y＝2x交于点B.(1)求点 B 的坐标；(2)求 sin∠BAO 的值．(第 3 题)利用同角或互余两角三角函数间的关系．若∠A 为锐角，且sin A＝3，则 cos A＝ ()42321 A．1 B. 2 C. 2 D.2125．若α为锐角，且cosα＝13，则sin(90°－α)＝()512512A.13B.13C.12D. 56．若α为锐角，且sin2α＋cos230°＝1，则α＝______．巧设参数47．在Rt△ABC中，∠C＝90°，若sin A＝5，则tan B的值为()4334A.3B.4C.5D.58．已知，在△ABC中，∠A，∠B，∠C所对的边长分别为a，b，c，且a，b，c 满足 b2＝ (c＋a)(c－a)．若 5b－ 4c＝0，求 sin A＋sin B 的值．利用等角来替换9．如图，已知Rt△ABC中，∠ACB＝90°，CD是斜边AB的中线，过点A 作AE ⊥CD，AE 分别与 CD， CB 相交于点 H，E 且 AH ＝2CH，求 sin B 的值．(第 9 题)专训 2同角或互余两角的三角函数关系的应用名师点金：2α＝1，tan α＝sinα．同角三角函数关系：21sinα＋cos.cos α2．互余两角的三角函数关系： sin α＝cos(90 °－α)，cos α＝sin(90 °－α)，tan α·tan(90 °－α)＝1.同角间的三角函数的应用sin A＝4，求sin A －3cos A1．已知cos A4sin A ＋cos A的值．22．若α为锐角，sinα－cosα＝2，求sinα＋cosα的值．余角的三角函数的用3．若45°－α和45°＋α均角，下列关系式正确的是()A．sin(45 °－α)＝sin(45 °＋α)22B．sin (45 °－α)＋cos (45 °＋α)＝122C．sin (45 °－α)＋sin (45 °＋α)＝122D．cos (45 °－α)＋sin (45 °＋α)＝14．算tan 1°·tan 2°·tan 3°·⋯·tan 88°·tan 89°的．同角的三角函数的关系在一元二次方程中的用125．已知sinα·cosα＝25(α 角)，求一个一元二次方程，使其两根分sin α和 cos α.26 ．已知α角且sinα 是方程2x － 7x ＋ 3 ＝ 0 的一个根，求3用三角函数解与有关名点金：用三角函数解与有关的，是近几年中考命内容，型多化；一般以中档、形式出，高度重．一、1．如，已知△ABC的外接⊙O的半径3，AC＝4，sin B＝() 1342A.3B.4C.5D.3(第 1 )(第 2 )2．如是以△ABC的AB直径的半O，点C恰好在半上，C作CD ⊥AB 交 AB于D，已知∠ACD＝3，BC＝4， AC 的 ()cos52016A．1 B. 3C．3 D. 343．在△ABC中， AB ＝ AC ＝5，sin B＝ 5.⊙O 过B，C 两点，且⊙O 半径r ＝10，则OA的长为 ()A．3 或5B． 5C．4 或 5D． 44．如图，在半径为 6 cm 的⊙ O 中，点 A 是劣弧 BC 的中点，点 D 是优弧BC 上一点，且∠ D＝30°.下列四个结论：(第 4 题)①OA⊥BC；②BC＝6 3 cm；3③sin∠AOB ＝2；④四边形 ABOC 是菱形．其中正确结论的序号是 ()A．①③ B．①②③④ C．②③④ D．①③④二、填空题5．如图，AB是⊙O的直径，AB＝15，AC＝9，则tan∠ADC＝________.(第 5 题)(第 6 题)6．如图，直线MN与⊙O相切于点M，ME＝EF且EF∥MN，则cos E＝________.7．如图，在半径为5的⊙O中，弦AB＝6，点C是优弧AB上的一点(不与A， B 重合 )，则 cos C 的值为 ________．(第 7 题)(第 8 题)8．如图，在直角坐标系中，四边形OABC是直角梯形，BC∥OA，⊙P分别与 OA ，OC， BC 相切于点 E，D， B，与 AB 交于点 F，已知 A(2 ，0)， B(1，2)，则 tan∠FDE＝________.三、解答题19．如图，Rt△ABC中，∠C＝90°，AC＝5，tan B＝2，半径为 2 的⊙ C 分别交 AC ，BC 于点 D， E，得到 .(1)求证： AB 为⊙ C 的切线；(2)求图中阴影部分的面积．(第 9 题)10．如图，AB是⊙O的直径，∠ABT＝45°，AT＝AB.(1)求证： AT 是⊙ O 的切线；(2)连接 OT 交⊙ O 于点 C，连接 AC ，求 tan∠TAC 的值．(第 10 题 )11.如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DE⊥AD 且与 AC 的延长线交于点 E.(1)求证： DC＝DE；1(2)若 tan∠CAB ＝2，AB ＝3，求 BD 的长．(第 11 题 )12．如图，以△ABC的一边AB为直径的半圆与其他两边AC，BC的交点分别为 D， E，且＝ .(1)试判断△ ABC 的形状，并说明理由；(2)已知半圆的半径为5，BC＝12，求 sin∠ABD 的值．(第 12 题 )13．如图，在四边形 ABCD 中，AB ＝AD ，对角线 AC ，BD 交于点 E ，点 O3在线段 AE 上，⊙ O 过 B ， D 两点，若 OC ＝ 5， OB ＝ 3，且 cos ∠BOE ＝5.求证： CB 是⊙ O 的切线．(第 13 题 )答案专训 1 1．CBD2．解： ∵AD ⊥BC ，∴ tan ∠BAD ＝AD .∵ t an ∠BAD ＝34，AD ＝12，∴34＝BD12 ，∴ BD ＝ 9. ∴CD ＝BC －BD ＝ 14－ 9＝5，∴在 Rt △ADC 中， AC ＝ AD 2＋CD 2＝ 122＋ 52＝13，AD 12∴sin C ＝AC ＝13.13y ＝ x ＋ ，x ＝1，3．解： (1)解方程组2 2得y ＝2x ，∴点 B 的坐标为 (1， 2)．(第 3 题)13(2)如图，过点 B 作 BC ⊥x 轴于点 C ，由 2x ＋ 2＝ 0，解得 x ＝－ 3，则 A( －3，0)，∴ OA ＝3， ∴AB ＝ AC 2＋BC 2＝2 5，∴ sin ∠ BAC ＝BC＝ 2 ＝ 5， AB2 5 55即 sin ∠BAO ＝ 5 .4．D 5.B 6.30° 7.B8．解： ∵b 2＝(c ＋ a)(c －a)，∴ b 2 ＝c 2－a 2，即 c 2＝a 2＋b 2，∴△ ABC 是直角三角形．∵5b －4c ＝0，∴ 5b ＝4c ，则bc ＝45，设 b ＝ 4k ，c ＝5k ，那么 a ＝ 3k.3k 4k 7∴sin A ＋sin B ＝ 5k ＋5k ＝ 5.9．解： ∵CD 是斜边 AB 的中线， ∴CD ＝AD ＝ BD. ∴∠ DCB ＝∠ B.∵∠ ACD ＋∠ DCB ＝90°，∠ ACD ＋∠ CAH ＝90°， ∴∠ DCB ＝∠ CAH ＝∠ B.在 Rt △ACH 中， AH ＝ 2CH ，CH5∴AC ＝ 5CH.∴sin B ＝sin ∠CAH ＝5CH ＝ 5 .专训 2sin Acos A ， 1．分析： 本题可利用 cos A 求解，在原式的分子、分母上同时除以sin Asin A＝ 4，把原式化为关于 cos A 的代数式，再整体代入求解即可．也可直接由cos A 得到 sin A 与 cos A 之间的数量关系，代入式子中求值．sin A －3解： (方法 1)原式＝ （sin A －3cos A ）÷cos A ＝ cos A （4sin A ＋cos A ）÷cos A 4sin A .＋1cos A sin A4－ 3 1∵cos A ＝ 4，∴原式＝ × ＋＝ 17.441方法 sin A＝4，∴ sin A ＝4cos A.(2)∵ cos A4cos A － 3cos A cos A1＝17cos A＝17.∴原式＝4×4cos A＋cos A2．分析：要求 sin α＋cos α的 ， 必 利用 角三角函数之 的关系找出它与已知条件的关系再求解．解： ∵sin α－ cos α＝ 2 2 12 ，∴ (sin α－cos α)＝2，即 sin 2α＋ cos 2α－ 2sin αcos α＝12.11∴1－2sin αcos α＝2，即 2sin αcos α＝2.2221 3α＋ 2sin αcos α＝1＋2＝ 2.∴(sin α＋cos α)＝sin α＋cos 又∵ α 角，∴ sin α＋cos α＞0.∴ s in α＋cos α＝ 26.3．C 点 ： ∵(45 °－α)＋(45 °＋α)＝90°，∴ sin (45 °－ α)＝cos (45 °＋α)， sin 2(45 °－α)＋sin 2(45 °＋ α)＝cos 2(45 °＋α)＋sin 2(45 °＋α)＝1.4．解： tan 1°·tan 2°·tan 3°·⋯·tan 88°·tan 89°＝ (tan 1°·tan 89°)·(tan 2°·tan88°)·⋯·(tan 44 °·tan 46 °)·tan 45 °＝1.点 ：互余的两角的正切 的 1，即若 α＋β＝ 90°， tan α·tan β＝ 1.5．解： ∵sin 2α＋ cos 2α＝1，sin α·cos α＝1225，2 2 21249∴(sin α＋cos α)＝sin α＋cos α＋ 2sin αcos α＝1＋2× 25＝25.7∵α 角，∴ sin α＋ cos α＞ 0.∴sin α＋cos α＝5.又∵ sin α·cos α＝1225，2 712∴以 sin α， cos α 根的一元二次方程x － 5x ＋25＝0.点 ：此 用到两方面的知 ： (1)公式 sin 2α＋cos 2α＝1 与完全平方公式的 合运用； (2)若 x 1＋x 2 ＝p ，x 1x 2＝ q ， 以 x 1 ，x 2 两根的一元二次方程 x 2 － px ＋q ＝026．解： ∵sin α是方程 2x －7x ＋ 3＝ 0 的一个根，－（－ 7） ± （－ 7）2－ 4× 2× 37±5 sin α＝2× 2＝ 4.∴sin α＝1或 sin α＝3(不符合 意，舍去 )．22221 2 3∵sin α＋cos α＝ 1，∴ cos α＝1－ 2 ＝4.3又∵ cos α＞ 0，∴ cos α＝ 2 .∴ 1－2sin αcos α＝ sin 2α＋cos 2α－ 2sin αcos α＝21 33－ 1（sin α－cos α） ＝|sin α－cos α|＝ 2－2 ＝2 .专训 3 一、 1.D2．D 点拨：∵AB 为直径， ∴∠ ACB ＝ 90°.又∵ CD ⊥ AB ，∴∠ B ＝∠ ACD.BC 3 20 2 2 16∴ cos B ＝AB ＝5，∴ AB ＝3 .∴AC ＝ AB －BC ＝ 3 .3．A 4.B3 141二、 5.4 6.2 7.5 8.2三、(第 9 题)AC9．(1)证明：如图，过点 C 作 CF ⊥AB 于点 F ，在 Rt △ABC 中， tan B ＝BC＝12，∴ BC ＝2AC ＝ 2 5.∴ AB ＝ AC 2＋BC 2＝ （ 5）2＋（ 2 5）2＝ 5，∴ CF· 5×2 5＝ AC BC＝＝2.∴ AB 为⊙ C 的切线．AB 51 n πr2 1 90π× 22(2)解： S 阴影 ＝S △ABC －S 扇形 CDE ＝2AC ·BC － 360 ＝2× 5× 2 5－ 360 ＝5－ π.10． (1)证明： ∵ AB ＝AT ，∴∠ ABT ＝∠ ATB ＝ 45°，∴∠ BAT ＝90°，即 AT 为⊙ O 的切线．AT(2)解：如图，过点 C 作 CD ⊥AB 于 D ，则∠ TAC ＝∠ ACD ，tan ∠ TOA ＝ AO＝ CD OD ＝ 2，设 OD ＝x ，则 CD ＝ 2x ，OC ＝ 5x ＝ OA. ∵AD ＝AO － OD ＝( 5－1)x ，∴ tan ∠TAC ＝tan ∠ACD ＝AD（ 5－1）x＝5－1＝2x2 .CD(第 10 题 )(第 11 题 )11． (1)证明：连接 OC ，如图，∵ CD 是⊙ O 的切线，∴∠ OCD ＝ 90°，∴∠ ACO ＋∠ DCE ＝ 90°.又∵ ED ⊥ AD ，∴∠ EDA ＝90°，∴∠ EAD ＋∠ E ＝90°.∵OC ＝OA ，∴∠ ACO ＝∠ EAD ，故∠ DCE ＝∠ E ，∴ DC ＝DE.(2)解：设 BD ＝x ，则 AD ＝AB ＋BD ＝3＋x ，OD ＝OB ＋ BD ＝ 1.5＋ x.在 Rt1 1 1 1△ EAD 中，∵tan ∠CAB ＝2，∴ED ＝2AD ＝ 2(3＋ x) ．由(1)知，DC ＝2(3＋x)．在Rt △ OCD 中，OC 2＋CD 2＝DO 2，则 1.52＋ 1（ 3＋ x ） 2 ＝(1.5＋x)2，解得 x 1＝－23(舍去 )， x 2＝1，故 BD ＝1.12． 解： (1)△ABC 为等腰三角形，理由如下：连接 AE ，如图， ∵＝，∴∠ DAE ＝∠ BAE ，即 AE 平分∠ BAC. ∵AB 为直径，∴∠ AEB ＝90°，∴ AE ⊥ BC ， ∴△ ABC 为等腰三角形．(2)∵△ ABC 为等腰三角形， AE ⊥BC ，1 1∴BE ＝CE ＝ 2BC ＝2×12＝ 6.在 Rt △ABE 中，∵ AB ＝10， BE ＝ 6，∴ AE ＝ 102－62＝8.∵AB 为直径，∴∠ ADB ＝90°，∴S △ABC＝ 1 · ＝1· ，∴BD ＝ 8×12＝ 482AE BC 2BD AC10 5 .在 Rt △ABD 中，∵ AB ＝10，BD ＝485，142 2 14AD 5 7 ∴AD ＝AB －BD ＝ 5 ，∴ sin ∠ABD ＝AB＝10＝25.(第 12 题 )(第 13 题 )13． 证明：如图，连接 OD ，可得 OB ＝ OD. ∵AB ＝AD ，∴ AE 垂直平分 BD.3 9在 Rt △BOE 中， OB ＝ 3， cos ∠BOE ＝ 5，∴ OE ＝ 5.16 ∴CE ＝OC －OE ＝ 5 .2212根据勾股定理得 BE ＝ BO －OE ＝ 5.在 Rt △CEB 中， BC ＝ CE 2＋BE 2＝4.∵OB ＝3， BC ＝ 4，OC ＝ 5，∴ OB 2＋BC 2 ＝OC 2， ∴∠ OBC ＝ 90°，即 BC ⊥OB ，∴ CB 为⊙ O 的切线．。

专题1.3 锐角三角函数（巩固篇）一、单选题知识点一、三角函数概念的辨析1．在△ABC 中，∠C ＝90°，∠A 、∠B 、∠C 的对边分别是a 、b 、c ，下列结论正确的是（ ） A ．b ＝a •sin AB ．b ＝a •tan AC ．c ＝a •sin AD ．a ＝c •cos B2．已知Rt ABC 中，90,C b ∠=︒为B ∠的对边，a 为A ∠的对边，若b 与A ∠已知，则下列各式正确的是（ ） A ．a bsin A =∠B ．a bcos A =∠C ．a btan A =∠D ．a b tan A =÷∠3．如图，EF 与AB ，BC ，CD 分别交于点E ，G ，F ，且1230∠=∠=︒，EF AB ⊥，则下列结论错误的是（ ）A ．//AB CDB ．360∠=︒C ．12FG FC =D ．GF CD ⊥4．如图，在菱形ABCD 中，DE ∠AB ，3cos 5A =，BE ＝2，则tan ∠DBE 的值是（ ）A ．12B ．2CD 知识点二、求三角函数值5．如图，ABC 的三个顶点都在边长为1的格点图上，则sin A 的值为（ ）A ．12B C D ．136．如图，正方形ABCD 的边长为6，AC 为对角线，取AB 中点E ，DE 与AC 交于点F ．则sin ∠DFC ＝（ ）A B C D 7．如图，点A 、B 、C 均在小正方形的顶点上，且每个小正方形的边长均为1，则cos BAC ∠的值为（ ）A ．12B C ．1 D 8．如图，已知E 是正方形ABCD 中AB 边延长线上一点，且AB BE =，连接CE 、DE ，DE 与BC 交于点N ，F 是CE 的中点，连接AF 交BC 于点M ，连接BF ．有如下结论：∠=DN EN ；∠ABF ECD ∽；∠1tan 3CED ∠=；∠=2CMFBEFM S S四边形，其中正确的是（ ）A ．∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠∠知识点三、由三角函数值求边长9．如图，ABC 中，CD AB ⊥，BE AC ⊥，sin A 的值为35，则DEBC =（ ）A B C ．35D ．4510．如图，在矩形ABCD 中，2AB =，BC =E 是BC 的中点，将ABE ∆沿直线AE 翻折，点落B 在点F 处，连结CF ，则CF 的长为（ ）A ．83B ．43C ．85D ．10311．如图：等腰Rt ABC 中，90,6,C AC D ∠=︒=是AC 上一点，若1tan 5DBA ∠=，则AD =（ ）．A B ．2C ．1D ．12．如图∠，在菱形ABCD 中，120D ∠=︒，点E 是AB 的中点，点P 是对角线AC 上一动点，设PC x =，PE PB y +=，图∠是y 关于x 的函数图像，且图像上最低点Q 的坐标为⎝，则菱形ABCD 的边长为（ ）A ．2B C ．D ．4知识点四、三角函数值的增减性13．角α，β满足045αβ<<<︒︒，下列是关于角α，β的命题，其中错误．．的是（ ）A ．0sin α<<B ．0tan 1β<<C ．cos sin βα<D ．sin cos βα<14．如图，撬钉子的工具是一个杠杆，动力臂1cos L L α=⋅，阻力臂2cos L l β=⋅，如果动力F 的用力方向始终保持竖直向下，当阻力不变时，则杠杆向下运动时的动力变化情况是（ ）A ．越来越小B ．不变C ．越来越大D ．无法确定15．下列命题：∠同位角相等；∠如果45°＜α＜90°，那么sinα＞cosα；∠若关于x 的方程322x mx -=+的解是负数，则m 的取值范围为m ＜﹣4；∠相等的圆周角所对的弧相等．其中假命题有（ ） A ．1个B ．2个C ．3个D ．4个16．下列结论中，不正确的是（ ） A ．sin4837cos4120'<'B ．Rt ABC ∆中，C 90∠=，则22sin A cos A 1+= C ．Rt ABC ∆中，C 90∠=，则cotBsinB cosB =D ．Rt ABC ∆中，C 90∠=，则BCAB sinB=知识点五、由函数值确实锐角的取值范围17．在菱形ABCD 中，过点A 作AE 与边BC 垂直于点E ，将∠ABE 沿直线AE 折叠，若点B 恰好落在线段EC 上（不与E ，C 重合），则∠B 的度数可以是（ ）A ．36°B ．60°C ．75°D ．100°18．如图，在Rt △ABC 中，∠ACB=90°，DE 是△ABC 的中位线，连结CD ．下列各组线段的比值一定与cosA 相等的是（ ）A ．DE ADB ．DE AEC ．CE BDD ．CE BC19．红领巾的形状是等腰三角形，底边长为100厘米，腰长为60厘米，则底角（ ） A ．小于30° B ．大于30°且小于45° C ．等于30°D ．大于45°且小于60°20．已知∠A 为锐角，且sin A ＜12，那么∠A 的取值范围是( )A ．0°＜∠A ＜30°B ．30°＜∠A ＜60°C ．60°＜∠A ＜90°D ．30°＜∠A ＜90° 二、填空题知识点一、三角函数概念的辨析21．如图，网格中的每一个正方形的边长都是1，△ABC 的每一个顶点都在网格的交点处，则sinC=_____．22．如图，在Rt ABC △中，90ACB ∠=︒，将ABC 沿BD 折叠，点C 恰巧落在边AB 上的C '处，折痕为BD ，再将其沿DE 折叠，使点A 落在DC '的延长线上的A '处．若BED 与ABC 相似，则相似比BDAC=________．23．如图，点B 在x 的正半轴上，且BA OB ⊥于点B ，将线段BA 绕点B 逆时针旋转60︒到BB '的位置，且点B '的坐标为()1,1．若反比例函数ky x=()0x >的图象经过A 点，则k =______．24．如图，在平面直角坐标系中，点1A ，2A ，3A ，…和1B ，2B ，3B ，…分别在直线15y x b =+和x 轴上．11OA B ，122B A B ，233B A B ，……都是等腰直角三角形，如果点()11,1A ，那么b 的值是________；2021A 的纵坐标是________．知识点二、求三角函数值25．如图，在Rt ABC 中，90ACB ∠=，D 是斜边AB 的中点，DE AC ⊥，垂足为E ，若2DE =，CD =cos CBE ∠的值为________．26．ABC ∆中，13AB AC ==，10BC =，则tan B =__．27．如图，在ABC 中，30,A E ∠=︒为AC 上一点，且:=3:1,AE EC EF AB ⊥于F ，连结FC ，则tan CFB ∠=_____．28．如图，ABC 中，,45,AB AC A AC =∠=︒的垂直平分线分别交,AB AC 于,D E 两点，连接CD ，如果2AD =，那么tan BCD ∠=______．知识点三、由三角函数值求边长29．如图，在∠ABC 中，∠A ＝90°，BC ＝10，sin∠B ＝35，D 是BC 边上的一个动点（异于B 、C 两点），过点D 分别作AB 、AC 边的垂线，垂足分别为E 、F ，则EF 的最小值是______．30．如图，矩形ABCD 中，AD ＝2，E 为CD 上一点，连接AE ，将∠ADE 沿AE 折叠，点D 恰好落在BC 上，记为D ′，再将∠D ′CE 沿D ′E 折叠，若点C 的对应点C ′落在AE 上，则AB 的长为___．31．如图，Rt ABC 中，390,tan 2BAC ABC ∠=︒∠=，将ABC 绕A 点顺时针方向旋转角9(0)0αα︒<<︒得到AB C ''△，连接BB '，CC '，则CAC '△与BAB '的面积之比等于_______．32．如图，折叠矩形ABCD ，使D 落在BC 边上的F 处，若折痕3tan 4AE EFC =∠=，则BC =_________．知识点四、三角函数值的增减性33．比较大小：81sin ____47tan ︒(填“<”“=”或“＞”)34．对于锐角,tan αα__________sin α．（填"",""""><=或）.35．从下面两题中只选做一题，如果做了两题的，只按第（1）题评分：（1）用“=＞”与“＜=”表示一种运算法则：（a=＞b ）=﹣b ，（a ＜=b ）=﹣a ，如（2=＞3）=﹣3，则（2010=＞2011）＜=（2009=＞2008）=________ （括号运算优先） （2）用“＞”或“＜”号填空：sin40°cos50°﹣12________ 0．（可用计算器计算） 36．已知∠B 是△ABC 中最小的内角，则tanB 的取值范围是_______． 知识点五、由函数值确实锐角的取值范围 37．若α为锐角，且13cos 2mα-=，则m 的取值范围是______________． 38．如图，在Rt ABC 中，30B ∠=︒，6BC =，点D 是BC 的中点，DEF 是等腰直角三角形，3DE DF ==，线段EF 与线段AB 相交于点Q ，将DEF 绕点D 逆时针转动，点E 从线段AB 上转到与点C 重合的过程中，线段DQ 的长度的取值范围______．39cosA ＜sin70°，则锐角A 的取值范围是_________ 40．函数()()2cos 4sin 6y x x θθ=-+对任意实数x 都有0y >，且θ是三角形的内角，则θ的取值范围是________三、解答题 41．如图，在ABCD 中，O 是对角线AC 、BD 的交点，BE AC ⊥，DF AC ⊥，垂足分别为点E 、F ．（1）求证：OE OF =．（2）若5BE =，2OF =，求tan OBE ∠的值．42．如图，在菱形ABCD 中，AC 为对角线，点E ，F 分别在AB ，AD 上，BE=DF ，连接EF ．（1）求证：AC∠EF ；（2）延长EF 交CD 的延长线于点G ，连接BD 交AC 于点O ，若BD=4，tanG=12，求AO 的长．43．如图，AD 是△ABC 的中线，tan B ＝13，cos C ＝2，AC 求：（1）BC的长；（2）sin ∠ADC的值．参考答案：1．D【分析】根据三角函数定义：（1）正弦：我们把锐角A 的对边a 与斜边c 的比叫做∠A 的正弦，记作sin A ．（2）余弦：锐角A 的邻边b 与斜边c 的比叫做∠A 的余弦，记作cos A ．（3）正切：锐角A 的对边a 与邻边b 的比叫做∠A 的正切，记作tan A ．分别进行分析即可．【详解】解：在直角△ABC 中，∠C ＝90°，则sin A ＝a c，则sin a c A =，故A 选项错误、C 选项错误； tan A ＝a b ，则b ＝tan a A，故B 选项错误； cos B ＝a c，则a ＝c cos B ，故D 选项正确； 故选：D ．【点睛】本题主要考查了锐角三角函数的定义，关键是熟练掌握锐角三角函数的定义．2．C【分析】利用锐角三角函数的定义列出算式，然后变形计算即可．【详解】解：如图所示：tanA=a b，则a=btan∠A ．故选：C ．【点睛】此题考查锐角三角函数的定义，掌握锐角三角函数的定义是解题的关键．3．C【分析】根据平行线的判定定理，可判断A ，根据平行线的性质，可判断B ，D ，根据锐角三角函数的定义，可判断C ，进而即可得到答案．【详解】解：∠1230∠=∠=︒，∠//AB CD ，故A 正确，不符合题意；∠EF AB ⊥，∠3180309060∠=︒-︒-︒=︒，故B 正确，不符合题意；∠//AB CD ，EF AB ⊥，∠EF CD ⊥，即：∠GFC =90°，故D 正确，不符合题意；又∠230∠=︒，∠tan30FGCF︒==，即：FG=，故C错误，符合题意．故选C．【点睛】本题主要考查平行线的判定和性质，锐角三角函数的定义，熟练掌握平行线的判定和性质，锐角三角函数的定义是解题的关键．4．B【分析】在直角三角形ADE中，3AE AB BEcos5AD ADA-===，求得AD，AE．再求得DE，即可得到tan∠DBE．【详解】设菱形ABCD边长为t．∠BE＝2，∠AE＝t−2．∠3AE AB BE cos5AD ADA-===，∠3t25t-=，∠t＝5．∠AE＝5−2＝3．∠DE4．∠tan∠DBE＝DE4=BE2＝2．故选：B．【点睛】本题考查了解直角三角形中三角函数的应用，要熟练掌握边角之间的关系．5．B【分析】根据网格的特点，找到B点所在网格的顶点D，连接BD，通过勾股定理的逆定理判断ABD△是直角三角形，进而根据正弦的定义求得sin A的值．【详解】如图，连接BD，根据网格的特点可知：AD AB BD ===22210,10AD BD AB ∴+==，∴ABD △是直角三角形，90ADB ∴∠=︒，sin BD A AB ∴== 故选B【点睛】本题考查了求一角的正弦，网格中证明三角形是直角三角形，勾股定理以及勾股定理的逆定理的应用，证明是ABD △是直角三角形解题的关键．6．A【分析】连接BD 与AC 交于点O ，利用勾股定理求得DE ，OD ，根据正方形的性质证明∠AFE ∠∠CFD ，然后根据相似三角形的性质求得DF ，进而可求．【详解】解：连接BD 与AC 交于点O ，∠四边形ABCD 为正方形，∠∠EAD ＝90°，AC ∠BD ，OD ＝12BD ，AB ∠CD ，AD ＝AB ＝CD ＝6， ∠∠DOF＝90°，∠EAF ＝∠DCF ，OD ＝∠E 为AB 中点，∠AE ＝12AB ＝12CD ＝3，由勾股定理得，DE∠∠EAF ＝∠DCF ，∠AFE ＝∠DFC ，∠∠AFE ∠∠CFD ， ∠12EF AE FD CD ==，∠DF ＝23DE ＝∠sin ∠DFC ＝OD DF ==， 故选：A ． 【点睛】本题考查了正方形的性质，相似三角形的判定与性质，勾股定理，解直角三角形，解题关键是构造直角三角形和找出相似三角形进行求解．7．B【分析】连接BC ，AB BC AC ，得到△ABC 是直角三角形，从而求解．【详解】如图，连接BC ，∠每个小正方形的边长均为1，∠由勾股定理得，AB BC ==AC =∠222+=，∠∠ABC 是直角三角形，∠cos AB BAC AC ∠==．故选：B ．【点睛】本题考查直角三角形，勾股定理；熟练掌握在方格中利用勾股定理求边长，同时判断三角形形状是解题的关键．8．D【分析】（1）证明△NCD ∽△NBE ，根据相似三角形的性质列出比例式，得到DN ＝EN ，判断①；根据两边对应成比例、夹角相等的两个三角形相似判断②；FG ⊥AE 于G ，根据等腰直角三角形的性质、正切的定义求出tan ∠F AG ，根据相似三角形的性质判断③；根据三角形的面积公式计算，判断④．【详解】解：∵四边形ABCD 为正方形，AB ＝BE ，∴AB ＝CD ＝BE ，AB ∥CD ，∴△NCD ∽△NBE ， ∴ND CD NE BE==1， ∴DN ＝EN ，故①结论正确；∵∠CBE ＝90°，BC ＝BE ，F 是CE 的中点，∴∠BCE ＝45°，BF 12=CE =，FB ＝FE ，BF ⊥EC ， ∴∠DCE ＝90°+45°＝135°，∠FBE ＝45°，∴∠ABF ＝135°，∴∠ABF ＝∠ECD ，∵DC CE =BF AB = ∴DC BF CE AB =， ∴△ABF ∽△ECD ，故②结论正确；作FG ⊥AE 于G ，则FG ＝BG ＝GE ， ∴13FG AG =， ∴tan ∠F AG 13FG AG ==， ∵△ABF ∽△ECD ，∴∠CED ＝∠F AG ，∴tan ∠CED 13=，故③结论正确； ∵tan ∠F AG 13=， ∴13BM AB =， ∴12BM MC =， ∴S △FBM 12=S △FCM ， ∵F 是CE 的中点，∴S △FBC ＝S △FBE ，∴S 四边形BEFM ＝2S △CMF ，故④结论正确；故选：D ．【点睛】本题考查的是相似三角形的判定和性质、三角形的面积计算，掌握相似三角形的判定定理和性质定理、三角形的面积公式是解题的关键．9．D【分析】根据CD AB ⊥，BE AC ⊥，可得ADC AEB ∽,进而可得ADE ACB ∽，进而可得DE AD BC AC=，根据已知条件设3CD a =，则5AC a =，求得AD ，即可求得答案． 【详解】CD AB ⊥，BE AC ⊥，∴90ADC AEB ∠=∠=︒，A A ∠=∠，∴ADC AEB ∽，AD AC AE AB∴=， A A ∠=∠，∴ADE ACB ∽，DE AD BC AC∴=， 3sin 5CD A AC==， 设3CD a =，则5AC a =，4AD a ∴，44=55DE AD a BC AC a ∴==． 故选D ．【点睛】本题考查了锐角三角函数的定义，勾股定理，相似三角形的性质与判定，根据两边成比例夹角相等证明三角形相似是解题的关键．10．D【分析】过点E 作EH ∠CF 于H ，根据折叠的性质得到∠AEB =∠AEF ，再根据点E 是BC 中点可得EF =EC ，可得∠EFC =∠ECF ，从而推出∠ECF =∠AEB ，求出cos ECF ∠，则2CF EC cos ECF =∠.【详解】解：如图所示，过点E 作EH ∠CF 于H由折叠可得：AB =AF =2，BE =EF ，∠AEB =∠AEF ，∠点E 是BC 中点，BC =∠BE =CE =EF∠∠EFC 为等腰三角形∠CF =2FH =2CH∠∠EFC =∠ECF ，AE =3==， ∠∠BEF =∠AEB +∠AEF =∠EFC +∠ECF ，∠∠ECF =∠AEB ，∠cos ECF ∠=cos AEB ∠=BE AE = ∠53CH CE cos ECF =∠= ∠CF =2CH =103故选D.【点睛】本题考查了矩形的性质和折叠的性质，以及余弦的定义，解题的关键是利用折叠的性质得到∠ECF =∠AEB .11．B【分析】过D 作DH ∠AB 于H ，由tan∠DBA =15，设DH =m ，则BH =5m ，AB =6m ，根据三角形ABC 是等腰直角三角形，∠C =90°，AC =6，可得AB ，从而可得6m ，解得m ，即可得到答案．【详解】解：过D 作DH ∠AB 于H ，如图：Rt∠BDH中，tan∠DBA=15，∠DHBH=15，设DH=m，则BH=5m，∠三角形ABC是等腰直角三角形，∠C=90°，AC=6，∠∠A=45°，AB∠∠AHD是等腰直角三角形，∠AH=m，AD m，∠AB=AH+BH=6m，∠6m，解得m∠AD=2．故选B．【点睛】本题主要考查解直角三角形，解题的关键是设DH=m，用含m的代数式表示AB，从而列方程求解．12．D【分析】连接DP根据轴对称性质PB PD=，由两点间线段最短可知D、P、E共线时PE+PB 最小，然后根据Q点的坐标，得到PC和DE的长，再利用∠D=120°，可得△ABD为等边三角形，利用锐角三角函数求出EB，得到AB的长即可．【详解】解：B、D关于直线AC对称，∴连接DP，PB PD=，PB PE PD PE DE ∴=+=＋，（点E ，D ，P 三点共线）∴PE PB +的值最小， 833,Q ⎛ ⎝，PC ∴=DE = ∠四边形ABCD 为菱形，DB 为对角线，∠D =120°，∠∠ADB =∠CDB =1602ADC ∠=︒，AD =AB ， ∠△ABD 为等边三角形，∠点E 为AB 中点，∠ED ∠AB ，∠∠EDB =30°，∠tan∠EDB =EB DE =∠2EB = ∠AB =2BE =4．故选D ．【点睛】本题查了菱形的性质，等边三角形的判定和性质，锐角三角函数，以及最短路径和函数图象问题，熟练掌握菱形的性质，等边三角形的判定和性质，以及最短路径和函数图象问题，是解题的关键．13．C【分析】由角α，β满足045αβ<<<︒︒，确定锐角三角函数的增减性，sin α随α的增大而增大，cos β随β的增大而减小，tan β随β的增大而增大，利用45°函数值的分点即可确定答案．【详解】解：角α，β满足045αβ<<<︒︒，sin α随α的增大而增大，cos β随β的增大而减小，tan β随β的增大而增大，A.∠sin 45︒sin α选项A 正确，不合题意； B ．∠tan 45=1︒,∠0tan 1β<<,选项B 正确，不合题意；C ．sin 45︒cos 45︒，cos 22βα><，cos sin βα>，选项C 不正确，符合题意；D ．sin 45=2︒，cos 45=2︒，cos 22αβ><，sin cos βα<，选项D 正确，不符合题意．故选择：C ．【点睛】本题考查锐角三角函数值的大小比较问题，掌握函数的增减性质利用45°函数值的特殊关系是解题关键．14．A【分析】根据杠杆原理及cos α的值随着α的减小而增大结合反比例函数的增减性即可求得答案．【详解】解：∠动力×动力臂=阻力×阻力臂，∠当阻力及阻力臂不变时，动力×动力臂为定值，且定值＞0，∠动力随着动力臂的增大而减小，∠杠杆向下运动时α的度数越来越小，此时cos α的值越来越大，又∠动力臂1cos L L α=⋅，∠此时动力臂也越来越大，∠此时的动力越来越小，故选：A ．【点睛】本题主要考查了杠杆原理以及锐角三角函数和反比例函数的增减性，熟练掌握相关知识是解决本题的关键．15．C【分析】分析是否为假命题，需要分别分析各题设是否能推出正确结论，不能推出正确结论的，即假命题．【详解】∠两直线平行，同位角相等，所以同位角相等是假命题；∠如果45°＜α＜90°，那么sinα＞cosα，所以∠是真命题；∠关于x 的方程322x m x -=+的解是x=4+m ， 因为x ＜0，∠4+m ＜0，解得m ＜-4，且m≠-6，即∠是假命题；∠在同圆或等圆中，相等的圆周角所对的弧相等，所以∠是假命题．所以假命题是∠∠∠，3个．故选C ．【点睛】主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．16．D【分析】根据锐角三角函数的定义与增减性逐一进行判断即可.【详解】A.正确，sin4837cos4123cos4120'''=<，锐角的角度越大，其余弦值越小，故选项错误；B.正确，同角的正弦值与余弦值的平方和等于1，故选项错误；C.正确，cotBsinB cosB BC AC BC AC AB AB ===，故选项错误； D.错误，AB=sin AC B，故选项正确. 故选D.【点睛】本题考点：锐角三角函数的定义与增减性.17．C【分析】在Rt∠ABE 中，得BE ＝AB •cos B ，则2BE ＝2AB •cos B ，根据点B 恰好落在线段EC 上，则有cos B ＜12，可得60°＜∠B ＜90°．【详解】解：如图：当∠B 为锐角时，在Rt∠ABE 中，BE ＝AB •cos B ，∠2BE ＝2AB •cos B ，∠点B 恰好落在线段EC 上，∠2BE ＜BC ，即2AB •cos B ＜BC ，∠cos B ＜12， ∠∠B ＞60°，∠60°＜∠B ＜90°，当∠B 为钝角时，折叠后B '不可能落在线段EC 上，故选：C ．【点睛】本题主要考查了菱形的性质、翻折的性质、以及三角函数的知识，证明出cosB ＜12是解题的关键．18．C【分析】根据特殊角锐角三角函数的定义以及直角三角形斜边上的中线性质即可求出答案．【详解】∠ED 是ABC 的中位线∠点D 、E 分别是AB 、AC 的中点∠90ACB ∠=︒∠CD BD AD ==∠A DCE ∠=∠ ∠CE CE A DCE C cos c Dos D B =∠== 故选：C【点睛】本题考查三角形综合问题，涉及直角三角形斜边上的中线性质，中位线的性质以及特殊角锐角三角函数的定义，本题属于中等题型．19．B【分析】过A 作AD BC ⊥于D ，根据等腰三角形的性质得到1502BD CD BC ===，根据三角函数的定义得到505cos 606B ==，再利用锐角三角函数的增减性进行判断进而得到结论． 【详解】如图，过A 作AD BC ⊥于D∠60AB AC == ∠1502BD CD BC === ∠505cos 606B ==56cos B ∠3045B ︒∠︒＜＜故选：B【点睛】本题考查了等腰三角形的性质锐角三角函数的定义以及性质，熟练掌握锐角三角函数的增减性是解题的关键．20．A【分析】根据特殊角的三角函数值求出sin30°=12，根据当∠A 是锐角时，其正弦随角度的增大而增大，【详解】∠∠A 为锐角，且sin30°=12，又∠当∠A 是锐角时，其正弦随角度的增大而增大，∠0°＜A ＜30°，故选A ．【点睛】考查了特殊角的三角函数值和锐角三角函数的增减性的应用，注意：当角是锐角时，其正弦和正切随角度的增大而增大，余弦和余切随角度的增大而减小．21 【分析】过A 作AD 垂直于BC ，利用勾股定理求出AC 的长，在直角三角形ACD 中，利用锐角三角函数定义求出sinC 的值即可.【详解】解：过A 作AD 垂直于BC 于D ，则AD=2，∠sinC=AD AC =【点睛】本题考查了锐角三角函数定义，牢记锐角三角函数定义是解本题的关键. 22．23【分析】根据BED 与ABC 相似，得到DBA A ∠=∠，又DBA DBC ∠=∠，得到30A DBC ∠=∠=︒，设BC 为x ，再根据三角函数的定义求得AC 、BD ，即可求解．【详解】解：BED 与ABC 相似，∠DBA A ∠=∠，又DBA DBC ∠=∠，∠A DBA DBC ∠=∠=∠，∠90A DBA DBC ∠+∠+∠=︒，∠30A DBC ∠=∠=︒，设BC 为x ，则tan30x AC ==︒，cos30x BD ==︒， ∠23BD AC = 故答案为23【点睛】此题考查了相似三角形的性质，三角函数的定义，熟练掌握相关基本性质是解题的关键．23．2+【分析】过点B′作B′D ∠x 轴于点D ，根据BA ∠OB 于点B 及图形旋转的性质求出∠B′BD 的度数，再由直角三角形的性质得出BD 及BB′的长，故可得出点A 的坐标，进而可得出结论．【详解】解：如图，过点B′作B′D ∠x 轴于点D ，∠BA ∠OB 于点B ，∠∠ABD ＝90°．∠线段BA 绕点B 逆时针旋转60°到BB′的位置，∠∠ABB′＝60°，∠∠B′BD ＝90°−60°＝30°．∠点B′的坐标为（1，1），∠OD ＝ B′D ＝1，∠BB′＝2B′D ＝2，BD ＝1tan30︒∠1OB =+AB ＝BB′＝2，∠(12)A ，∠2(12k =⨯=+故答案为：2+【点睛】本题考查的是坐标与图形变化−旋转，根据题意作出辅助线，利用锐角三角函数的定义得出A 点坐标是解答此题的关键．24． 45 （32）2020 【分析】利用待定系数法可得b 的值，确定一次函数的解析式，设直线1455y x =+与x 轴的交点为G ，过点A 1，A 2，A 3分别作x 轴的垂线，垂足分别为D 、E 、F ，由条件可求得312A F A D A E GD GE GF==，再根据等腰三角形可分别求得A 1D 、A 2E 、A 3F ，可得到A 2，A 3的纵坐标坐标，找出规律得An 的纵坐标，进而即可求解．【详解】解：∠()11,1A 在直线15y x b =+上， ∠1115b =⨯+，解得：b =45， ∠直线的解析式为：1455y x =+， 设直线1455y x =+与x 轴的交点为G ， 令y ＝0可解得x ＝−4，∠G 点坐标为（−4，0），∠OG ＝4，过点A 1，A 2，A 3分别作x 轴的垂线，垂足分别为D 、E 、F ，∠∠A 1B 1O 为等腰直角三角形，∠A 1D ＝OD ，∠OB 1=2A 1D =2，∠GB 1=2+4=6，又∠点A 1在直线1455y x =+上， ∠tan∠A 1GO =1A D GD =215A E GE =，即22115A E A E GB =+， 解得： A 2E ＝32＝（32）1，则OE ＝OB 1＋B 1E ＝72， ∠A 2（72，32），OB 2＝5， 同理可求得：A 3F ＝94＝（32）2，则OF ＝5＋94＝294， ∠A 3（294，94），∠当A n 时其纵坐标为（32）n −1，即：2021A 的纵坐标是：（32）2020， 故答案是：45，（32）2020． 【点睛】本题主要考查等腰三角形的性质和直线上点的坐标特点，根据题意找到点的纵坐标的变化规律是解题的关键，注意观察数据的变化．25．45##0.8【分析】先求解CD BD AD AB ====再证明,CE AE = 利用勾股定理求解,,,CE BC BE 再利用余弦的定义可得答案．【详解】解：90ACB ∠=，D 是斜边AB 的中点，CD =CD BD AD AB ∴====DE AC ⊥，2DE =3CE ∴，∠∠CAD 是等腰三角形，DE AC ⊥，3,6,AE CE AC ∴===在Rt ABC 中，4,BC =在Rt BCE △中，5,BE =4cos .5BC CBE BE ∴∠== 故答案为：45． 【点睛】本题考查的是直角三角形斜边上的中线的性质，等腰三角形的性质，勾股定理的应用，求角的余弦，熟练的运用勾股定理求值是解题的关键．26．125【分析】根据题意画出图形，由等腰三角形的性质求出BD 的长，根据勾股定理求出AD 的长，再根据锐角三角函数的定义即可求出tan B 的值．【详解】解：如图，等腰ABC ∆中，13AB AC ==，10BC =，过A 作AD BC ⊥于D ，则5BD =，在Rt ABD ∆中，13AB =，5BD =，则，12AD ==， 故12tan 5AD B BD ==． 故答案为125．【点睛】本题考查了勾股定理，等腰三角形的性质和三角函数的应用，关键是将问题转化到直角三角形中求解，并且要熟练掌握好边角之间的关系．27【分析】作CD AB ⊥，将tan CFB ∠的值转化为CD 与FD 的比，根据题中所给的条件，在直角三角形中解题，根据角的正切值与三角形边的关系，代入三角函数进行求出CD 与FD 的长．【详解】解：如图，作出CD AB ⊥，垂足为D ，则//EF CD ，∴设EC x =，则3AE x =，sin sin30:1:2A EF AE =︒==，32EF x ∴=，cos cos30:A AF AE =︒==AF ∴． //EF CD ， ∴3AE AF EC FD ==，34AE EF AC CD ==，3AF FD ∴==，423CD EF x ==，tan CD CFB FD ∴∠=．【点睛】本题考查了比例线段性质和锐角三角函数的概念，熟悉相关性质是解题的关键． 281【分析】先证明∠BCD 为直角三角形，再运用三角函数定义求解．【详解】解：∠DE 是AC 的垂直平分线，∠AD=DC =2，∠AED =90°，∠∠A =45°,∠∠ACD =45°，∠∠BDC =∠A +∠ACD =90°，∠∠ADC=90°，∠AC ==∠AB =2BD =，∠tan ∠BCD =1BD CD ==，1．【点睛】本题考查三角形的综合应用，熟练掌握垂直平分线的性质、三角形的外角性质和正切函数的定义是解题关键．29．245【分析】连接AD ，先由锐角三角函数定义求出AC ＝6，则AB ＝8，再证四边形AEDF 是矩形，则EF ＝AD ，当AD ∠BC 时，AD 的值最小，然后由面积法即可求解．【详解】解：如图，连接AD ，在∠ABC 中，∠A ＝90°，BC ＝10，sin∠B ＝35＝AC BC， ∠AC ＝35BC ＝6，∠AB 8，∠DE ∠AB ，DF ∠AC ，∠∠DEA ＝∠DF A ＝∠A ＝90°，∠四边形AEDF 是矩形，∠EF ＝AD ，当AD ∠BC 时，AD 的值最小，此时EF 最小值＝AD ＝AB C AC B ⨯＝8610⨯＝245， 故答案为：245．【点睛】本题考查的是三角形的动点问题，熟练掌握相似三角形和勾股定理是解题的关键． 30【分析】由折叠的性质得到ADE AD E D CE D C E ∆∆⎧⎨∆∆'''⎩'≌≌，能得到345∠=∠=∠，再用平角的性质得到34560∠=∠=∠=︒，再由1490∠+∠=︒，得到1230∠=∠=︒，可以求出6∠，最后可以求出cos AB AD BAD ''=⨯∠．【详解】如图：由折叠的性质得：ADE AD E D CE D C E∆∆⎧⎨∆∆'''⎩'≌≌∠123435AD AD ∠=∠∠=∠=⎧⎨∠=∠'⎩；； ∠345∠=∠=∠∠345180∠+∠+∠=︒∠34560∠=∠=∠=︒∠1490∠+∠=︒∠1230∠=∠=︒∠6901230∠=︒-∠-∠=︒∠'Rt ABD 中，'30BAD ∠=︒∠cos cos AB AD BAD AD BAD '''=⨯∠=⨯∠2==【点睛】本题考查了矩形与折叠，全等三角形的性质，三角函数，掌握它们的性质是解题的关键．31．9:4 【分析】先根据正切三角函数的定义可得32AC AB =，再根据旋转的性质可得,,AB AB AC AC BAB CAC α''''==∠=∠=，从而可得1AC AB AC AB ==''，然后根据相似三角形的判定可得CAC BAB ''~，最后根据相似三角形的性质即可得． 【详解】解：在Rt ABC 中，390,tan 2BAC ABC ∠=︒∠=， 32AC AB ∴=， 由旋转的性质得：,,AB AB AC AC BAB CAC α''''==∠=∠=，1AC AB AC AB ∴==''， 在CAC '△和BAB '中，AC AB AC AB CAC BAB ''''⎧=⎪⎨⎪∠=∠⎩，CAC BAB ''~∴，294CAC BAB AC S AB S ''⎛⎫== ⎪⎝⎭∴，即CAC '△与BAB '的面积之比等于9:4，故答案为：9:4．【点睛】本题考查了正切三角函数、旋转的性质、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题关键．32．10【分析】根据tan ∠EFC =34，设CE =3k ，在RT ∠EFC 中可得CF =4k ，EF =DE =5k ，根据∠BAF =∠EFC ，利用三角函数的知识求出AF ，然后在RT ∠AEF 中利用勾股定理求出k ，继而代入可得出答案．【详解】解：∠tan ∠EFC =34，设CE =3k ，则CF =4k ，由勾股定理得EF =DE =5k ，∠DC =AB =8k ，∠∠AFB +∠BAF =90°，∠AFB +∠EFC =90°，∠∠BAF =∠EFC ，∠tan ∠BAF =tan ∠EFC =34， ∠BF =6k ，AF =BC =AD =10k ，在Rt ∠AFE 中，由勾股定理得AE =解得：k =1，∠BC =10×1=10；故答案为：10．【点睛】本题考查了翻折变换的性质、矩形的性质、勾股定理；解答本题关键是根据三角函数值，表示出每条线段的长度，然后利用勾股定理进行解答．33．<【分析】根据三角函数的性质得sin811tan 47tan 451︒<︒>︒=，，即可比较它们的大小关系． 【详解】∠sin811tan 47tan 451︒<︒>︒=， ∠8147sin tan <︒故答案为：<．【点睛】本题考查了三角函数值大小比较的问题，掌握三角函数的性质是解题的关键．34．>【分析】根据锐角三角函数正弦、余弦、正切之间的关系，列示解决即可. 【详解】sin tan cos a aaa 角是锐角， 0cos 1a ∴<<sin sin cos a a a∴> tan sin a a ∴>故答案是＞.【点睛】本题考查了锐角三角函数，熟练掌握三个锐角函数之间的关系是解决本题的关键.35． 2011 ＜【分析】（1）首先认真分析找出规律，然后再代入数值计算．（2）根据cosα=sin （90°-α）和三角函数的增减性计算．【详解】解：（1）（2010=＞2011）与（2009=＞2008）都符合公式：（a=＞b ）=-b ， ∠（2010=＞2011）=-2011，（2009=＞2008）=-2008，∠（2010=＞2011）＜=（2009=＞2008）=（-2011）＜=（-2008），（-2011）＜=（-2008）符合公式（a ＜=b ）=-a ，∠（-2011）＜=（-2008）=2011．（2）∠90°＞40°＞0°，∠cos50°=sin （90°-50°）=sin40°，∠原式=（sin40°）2﹣12，又∠（sin40°）2＜（sin45°）2=2⎝⎭， ∠（sin40°）2＜12， 即（sin40°）2﹣12＜0． 【点睛】（1）解决此类问题时，主要运用等量代换思想，即要看准用哪一个数字代替哪一个字母．（2）考查了锐角三角函数的关系和增减性．36．0＜【分析】在三角形中，最小的内角应不大于60度，找到相应的正切值即可，再根据tan60°=【详解】解：根据三角形的内角和定理，易知三角形的最小内角不大于60°．根据题意，知：0°＜∠B≤60°．又∠0＜故答案为: 0＜【点睛】此题主要考查了三角形的内角和定理、特殊角的锐角三角函数值和锐角三角函数值的变化规律，得出0°＜∠B≤60°是解题关键．37．11 33m-<<【分析】根据“0＜锐角三角函数的余弦值＜1”列出不等式，解不等式即可求得m的取值范围.【详解】α是锐角，且且13 cos2mα-=，则有0＜132m-＜1，解得，13-＜m＜13.故答案为13-＜m＜13.【点睛】本题考查了利用锐角三角函数的值求参数的取值范围，熟知“0＜锐角三角函数的余弦值＜1”是解决本题的关键.383DQ≤≤【分析】由旋转的性质可得DE=CD=3，由点Q在EF上运动，可得当点Q与点E重合时，DQ有最大值为3，当DQ∠EF时，DQ有最小值，由锐角三角函数可求解．【详解】解：∠BC=6，点D是BC的中点，∠CD=BD=3，∠将∠DEF绕点D逆时针转动，点E从线段AB上转到与点C重合，∠DE =CD =3，∠线段EF 与线段AB 相交于点Q ，∠点Q 在EF 上运动，∠当点Q 与点E 重合时，DQ 有最大值为3，如图，连接DQ ，当DQ ∠EF 时，DQ 有最小值，∠∠DEF 是以点D 为直角顶点的等腰直角三角形，∠∠E =45°，sin DQ E DE ∴==DQ DE ∴==∠DQ 的最小值为23,DQ ≤≤3,DQ ≤≤ 【点睛】本题考查了旋转的性质，等腰三角形的性质，三角函数，利用垂线段最短解决问题是本题的关键．39．20°＜∠A ＜30°．【详解】cosA ＜sin70°，sin70°=cos20°， ∠cos30°＜cosA ＜cos20°，∠20°＜∠A ＜30°．40．060θ<<【分析】因为cosθ＞0，所以只要∠＜0，函数值恒为正．由∠＜0，得到三角函数不等式，再把正弦转化为余弦，解不等式，最后利用三角函数的增减性求出θ的取值范围．【详解】解：由题意得：0162240cos sin cos θθθ⎧⎨-⎩＞＝＜即：()021230cos cos cos θθθ⎧⎨--⎩＞＜，（2cosθ-1）（cosθ+2）＞0，解得cosθ＞12，又因为0°＜θ＜180°， 所以θ的取值范围为0°＜θ＜60°．故答案是：0°＜θ＜60°．【点睛】考查了一元二次方程ax 2+bx+c=0（a≠0，a ，b ，c 为常数）根的判别式．当∠＞0，方程有两个不相等的实数根；当∠=0，方程有两个相等的实数根；当∠＜0，方程没有实数根．同时考查了锐角三角函数的性质，锐角的余弦随着角度的增大而减小；同角的正余弦的平方和为1．记住特殊角的三角函数值．41．（1）见解析1；（2）25【分析】（1）根据题意由平行四边形性质得OD OB =，由ASA 证得DFO BEO ∆∆≌，即可得出结论；（2）根据题意由（1）得OE=OF ，则OE=2，在Rt∠OEB 中，由三角函数定义即可得出结果．【详解】解：（1）证明：在ABCD 中，OD OB =∠BE AC ⊥，DF AC ⊥∠DF BE ∥∠FDO EBO ∠=∠又∠DOF BOE ∠=∠∠()DFO BEO ASA ∆∆≌∠OE OF =（2）∠OE OF =，2OF =∠2OE =∠BE AC ⊥∠90OEB ∠=︒在Rt OBE ∆中，5BE =，2tan 5OE OBE BE ∠==. 【点睛】本题考查平行四边形的性质、全等三角形的判定与性质、三角函数定义等知识；熟练掌握平行四边形的性质与全等三角形的判定是解题的关键．42．（1）证明见解析；（2）AO=1．【分析】（1）由菱形的性质得出AB=AD ，AC 平分∠BAD ，再根据等腰三角形的三线合一即可；（2）根据菱形的性质和已知条件得出四边形EBDG 为平行四边形，得出∠G=∠ABD ，再根据tanG=12即可求出AO 的长．【详解】（1）证明：∠四边形ABCD 为菱形 ∠AB=AD ，AC 平分∠BAD∠BE=DF ， ∠AB BE AD DF -=- ， ∠AE=AF∠∠AEF 是等腰三角形， ∠AC 平分∠BAD ， ∠AC∠EF（2）解：如图2所示：∠四边形ABCD 为菱形，∠CG∠AB ，BO=12BD=2，∠EF∠BD ∠四边形EBDG 为平行四边形，∠∠G=∠ABD ，∠tan∠ABD=tan∠G=12∠tan∠ABD=122AO AO BO ==，∠AO=1 【点睛】本题考查了菱形的性质、平行线的判定与性质、解直角三角形，等腰三角形的性质等知识；熟练掌握菱形的性质是解题的关键．43．（1）BC ＝4；（2）sin ∠ADC ＝2. 【详解】（1）如图，作AE∠BC ，。

2023年中考九年级数学高频考点专题训练--锐角三角函数一、综合题1．如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交∠O于E，D为BE延长线上一点，且∠DAE＝∠FAE.（1）求证：AD为∠O切线；（2）若sin∠BAC＝35，求tan∠AFO的值.2．如图，一个正方体木箱沿斜面下滑，正方体木箱的边长BE为2m，斜面AB的坡角为∠BAC，且tan∠BAC= 3 4．（1）当木箱滑到如图所示的位置时，AB=3m，求此时点B离开地面AC的距离；（2）当点E离开地面AC的距离是3.1m时，求AB的长．3．如图，在∠ABC中，∠A＝30°，∠C＝90°，AB＝12，四边形EFPQ是矩形，点P与点C重合，点Q、E、F分别在BC、AB、AC上（点E与点A、点B均不重合）．（1）当AE＝8时，求EF的长；（2）设AE＝x，矩形EFPQ的面积为y．①求y与x的函数关系式；②当x为何值时，y有最大值，最大值是多少？（3）当矩形EFPQ的面积最大时，将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动（当点P到达点B时停止运动），设运动时间为t秒，矩形EFPQ与∠ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．4．如图，以∠ABC的一边AB为直径的半圆O与边AC，BC的交点分别为点E，点D，且D是BE⌢的中点．（1）若∠A＝80°，求∠DBE的度数．（2）求证：AB＝AC．（3）若∠O 的半径为5cm，BC＝12cm，求线段BE的长．5．如图，抛物线y=﹣x2+bx+c过点B（3，0），C（0，3），D为抛物线的顶点．（1）求抛物线的解析式以及顶点坐标；（2）如果点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点，连接BC，BE，求tan∠CBE的值；（3）点M是抛物线对称轴上一点，且∠DAM和∠BCE相似，求点M坐标．6．如图，已知tan∠EOF=2，点C在射线OF上，OC=12．点M是∠EOF内一点，MC∠OF于点C，MC=4．在射线CF上取一点A，连结AM并延长交射线OE于点B，作BD∠OF于点D．（1）当AC的长度为多少时，∠AMC和∠BOD相似；（2）当点M恰好是线段AB中点时，试判断∠AOB的形状，并说明理由；（3）连结BC．当S∠AMC=S∠BOC时，求AC的长．7．如图1，在∠ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点(不与A 重合)，连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM，射线AE于点F，D．（1）直接写出∠NDE的度数；（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，(1)中的结论是否发生变化?如果不变，选取其中一种情况加以证明；如果变化，请说明理由；，其他条件不（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD= √6+√22变，求线段AM的长．8．（1）【基础巩固】如图1，在∠ABC中，D，E，F分别为AB，AC，BC上的点，DE∠BC，BF=CF，AF交DE于点G，求证：DG= EG．（2）【尝试应用】如图2，在(1)的条件下，连结CD，CG．若CG∠DE，CD=6，AE=3，求DEBC的值．（3）【拓展提高】如图3，在∠ABCD中，∠ADC=45°，AC与BD交于点O，E为AO上一点，EG∠BD交AD于点G，EF∠EG交BC于点F．若∠EGF=40°，FG平分∠EFC，FG=10，求BF的长．9．在锐角∠ABC中，AB=4，BC=5，∠ACB=45°，将∠ABC绕点B按逆时针方向旋转，得到∠DBE．（1）当旋转成如图①，点E在线段CA的延长线上时，则∠CED的度数是度；（2）当旋转成如图②，连接AD、CE，若∠ABD的面积为4，求∠CBE的面积；（3）点M为线段AB的中点，点P是线段AC上一动点，在∠ABC绕点B按逆时针方向旋转过程中，点P的对应点P′，连接MP′，如图③，直接写出线段MP′长度的最大值和最小值．10．如图，在矩形ABCD中，AB＝8，BC＝6，点E，F分别从点B，D同时出发沿AB延长线和射线DA以相同的速度运动，连结EF，交射线DB于点G.连结CG.（1）当BE＝2时，求BD，EG的长.（2）当点F在线段AD上时，记∠DCG为∠1，∠AFE为∠2，那么tan∠1tan∠2的值是否会变化？若不变，求出该比值；若变化，请说明理由.（3）在整个运动过程中，当∠DCG为等腰三角形时，求BE长.11．我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A＝75°，∠D＝85°，则∠C ＝．（2）已知：在“等对角四边形”ABCD中，∠DAB＝60°，∠ABC＝90°，AB＝4，AD＝3．求对角线AC的长．（3）已知：如图2，在平面直角坐标系xOy中，四边形ABCD是“等对角四边形”，其中A（﹣2，0）、C（2，0）、B（﹣1，﹣√3），点D在y轴上，抛物线y＝ax2+bx+c（a＜0）过点A、D，且当﹣2≤x≤2时，函数y＝ax2+bx+c取最大值为3，求二次项系数a的值．12．如图，已知BC为∠O的直径，点D为CE⌢的中点，过点D作DG∠CE，交BC的延长线于点A，连接BD，交CE于点F．（1）求证：AD是∠O的切线；（2）若EF＝3，CF＝5，tan∠GDB＝2，求AC的长．13．已知：如图，AB为∠O的直径，C是BA延长线上一点，CP切∠O于P，弦PD∠AB于E，过点B作BQ∠CP于Q，交∠O于H，（1）如图1，求证：PQ＝PE；（2）如图2，G是圆上一点，∠GAB＝30°，连接AG交PD于F，连接BF，若tan∠BFE＝3√3，求∠C的度数；（3）如图3，在（2）的条件下，PD＝6 √3，连接QC交BC于点M，求QM的长．14．定义：一边上的中线与另一边的夹角为30°的三角形称作美妙三角形。