2011浙江省一级重点中学自主招生仿真试题1

2011年全国重点高中自主招生试题选一、选择题3. (2011年浙江湖州安吉重点高中自主招生试题）如果在载玻片上写一个字如图甲所示，用显微镜观察，怎样能使图象变成图乙？（）BA.将载玻片顺时针转动90°B.将载玻片逆时针转动90°C.将载玻片向左上角移动D.将载玻片向右下角移动4 ．(2011年浙江湖州安吉重点高中自主招生试题）铁路提速要解决的一个重要技术问题就是提高机车牵引力功率。

已知匀速行驶时，列车所受阻力与速度的平方成正比，即f =kv2，当列车分别以180k m/h 和60km/h的速度在水平轨道上匀速行驶时，机车的牵引力功率之比为（）CA.3:1B.9:lC.27:1D.81:l5.(2011年浙江湖州安吉重点高中自主招生试题）如图，在一凸透镜左侧放一厚矩形玻璃砖，当平行光从右边射来通过玻璃砖时，其聚焦位置较无此玻璃砖时（）AA.向左移B.向右移C.不变D.无法确定6.(2011年浙江湖州安吉重点高中自主招生试题）宇宙飞船关闭发动机后在大气层外绕地球飞行时，飞船内可能出现的现象是（）DA.物质的质量消失B.蜡烛正常燃烧C.物体自由下落的速度变快D.水滴可以呈球形漂浮在空中7.(2011年浙江湖州安吉重点高中自主招生试题）如图，甲与乙是两只完全相同的金属球，A悬挂在不计热膨胀的绝热细线下，B 放在不计热膨胀的绝热桌面上，当A 、B 两球升高相同的温度后，结合能的转化和守恒定律，可以判断A 、B 所吸收的热量（）CA.Q A=Q BB.Q A> Q BC.Q A＜Q BD.不能确定8.(2011年浙江湖州安吉重点高中自主招生试题）某著名运动器材厂商为世界杯的足球明星设计了一种新球鞋，穿这种鞋踢球能加强球在空中的旋转。

据说这种鞋的表面设计了一些特殊的凹凸图纹，这主要是为了（）DA.增加弹性B.美观C.减少阻力D.增加摩擦力9.(2011年浙江湖州安吉重点高中自主招生试题）把一重为G的物体，用一个水平的推力F=kt（k 为常量，t为时间）压在竖直的足够高的平整的墙上（如图），从t=0开始物体所受的摩擦力f随t的变化关系可能是下图中的（）B10.(2011年浙江湖州安吉重点高中自主招生试题）两只灯泡L A和L B额定电压都是110V，额定功率分别是100W和60W，要求把它们接入220V的电路上都能正常发光，且整个电路消耗的功率最小，可采用下面哪种电路（）C15.(2011年浙江湖州安吉重点高中自主招生试题）在两个相同的薄壁塑料瓶（质量忽略不计）内分别装入体积相等、密度为ρ甲和ρ乙的两种液体后密封，再把它们放入两个装有水的容器中，处于如图所示状态。

浙江省省一级重点中学自主招生考试数学模拟试卷参考答案与试题解析一、选择题（共8小题，每题只有一个正确选项，每小题5分，共40分）1．（5分）方程实数根的情况是（）A．仅有三个不同实根B．仅有两个不同实根C．仅有一个不同实根D．无实根考点：二次函数的图象；反比例函数的图象．专题：计算题．分析：原方程有意义，则x≠0，把方程去分母、整理可得，x3﹣2x2+2x﹣1=0，分解因式得（x﹣1）（x2﹣x+1）=0，讨论其根的情况，即可解答．解答：解：原方程整理得，x3﹣2x2+2x﹣1=0，∴（x﹣1）（x2﹣x+1）=0，∵方程x2﹣x+1=0，其△＜0，无解，∴x2﹣x+1≠0，∴x﹣1=0，即x=1．故选C．点评：本题考查了二次函数、反比例函数的性质，主要应用了一元二次方程的根与判别式△的关系．2．（5分）将矩形纸片ABCD对折，得折痕MN，再把点B叠在折痕MN上，得折痕AE，若AB=，则折痕AE的长为（）A．B．2C．D．2考点：翻折变换（折叠问题）．分析：首先由矩形纸片ABCD对折，得折痕MN，推出∠BMN=∠AMN=90°，∠CNM=∠DNM=90°，M为AB的中点，然后根据矩形的性质推出∠BAD=∠B=∠C=∠D=90°，即可推出AD∥MN∥BC，H点为AE的中点，根据翻折变换的性质，结合题意推出AB=AB′=，∠BAE=∠B′AE，∠B=∠EB′A=90°，那么在Rt△AEB′中，AH=EH=B′H，得出∠EAB′=∠HB′A，根据平行线的性质推出∠DAB′=∠HB′A，通过等量代换可推出∠B′AE=∠EAB=B′AD=30°，最后根据特殊角的三角函数值即可推出AE的长度．解答：解：如图，设MN和AE交于点H，∵矩形ABCD，∴∠BAD=∠B=∠C=∠D=90°，∵矩形纸片ABCD对折，得折痕MN，∴∠BMN=∠AMN=90°，∠CNM=∠DNM=90°，M为AB的中点，∴AD∥MN∥BC，H点为AE的中点，∵点B叠在折痕MN上，得折痕AE，AB=，∴AB=AB′=，∠BAE=∠B′AE，∠B=∠EB′A=90°，∴在Rt△AEB′中，AH=EH=B′H，∴∠EAB′=∠HB′A，∵AD∥MN∥BC，∴∠DAB′=∠HB′A，∴∠B′AE=∠EAB=B′AD=30°，∵在Rt△BAE中，AB=，∠BAE=30°，∴AE=2．故选择B．点评：本题运用的知识点较多，主要考查翻折变换的性质，平行线的判定及性质，直角三角形的斜边上的中线的性质，矩形的性质，中点的性质，特殊角的三角函数值等知识点的综合运用，关键在于熟练运用相关的性质定理推出AH=EH=B′H，∠B′AE=∠EAB=B′AD=30°，运用特殊角的三角函数值认真的进行求解即可．3．（5分）在半径为1的圆O中，弦AB、AC的长分别为、，则∠BAC的度数为（）A．60°B．75°C．60°或45°D．15°或75°考点：垂径定理；解直角三角形．专题：分类讨论．分析：先根据题意画出图形，分别作AC、AB的垂线，连接OA，再根据锐角三角函数的定义求出∠AOD及∠AOE的度数，根据直角三角形的性质即可得出结论．解答：解：①如图1，两弦在圆心的异侧时，过O作OD⊥AB于点D，OE⊥AC于点E，连接OA，∵AB=，AC=，∴AD=，AE=，根据直角三角形中三角函数的值可知：sin∠AOD=，∴∠AOD=45°，∵sin∠AOE=，∴∠AOE=60°，∴∠OAD=90°﹣∠AOD=45°，∠OAC=90°﹣∠AOE=30°∴∠BAC=∠OAD+∠OAC=45°+30°=75°；②如图2，当两弦在圆心的同侧时同①可知∠AOD=45°，∠AOE=60°，∴∠AOE=60°，∴∠OAC=90°﹣∠AOE=90°﹣60°=30°，∠OAB=90°﹣∠AOD=90°﹣45°=45°．∴∠BAC=∠OAB﹣∠OAC=45°﹣30°=15°．故选D．点评：本题考查的是垂径定理及勾股定理，解直角三角形，锐角三角函数的定义及特殊角的三角函数，解答此题时要注意分类讨论，不要漏解．4．（5分）如图，一个半径为3的圆O1的圆心经过一个半径为3的圆O2，则图中阴影部分的面积为（）A．B．9C．D．考点：扇形面积的计算；勾股定理；相交两圆的性质．专题：计算题．分析：连接O1O2，O1A，O1B，O2A，O2B，由勾股定理的逆定理得∠O2CA=∠AO2B=90°，则点A、O1、B在同一条直线上，则AB是圆O1的直径，从的得出阴影部分的面积S阴影=S⊙1﹣S弓=S⊙1﹣（S扇形AO2B﹣S△AO2B）．形AO1B解答：解：连接O1O2，O1A，O1B，O2A，O2B，∵CO2=CA=3，O2A=，∴CO22+CA2=O2A2，∴∠O2CA=90°，同理∠O2CB=90°，∴点A、C、B在同一条直线上，并且∠AO2B=90°，∴AB是圆O1的直径，∴S阴影=S⊙1﹣S弓形AO1B=S⊙1﹣（S扇形AO2B﹣S△AO2B）==9．故选B．点评：本题考查了扇形面积的计算、勾股定理和相交两圆的性质．5．（5分）已知A，B是两个锐角，且满足，，则实数t所有可能值的和为（）A．B．C．1D．考点：根与系数的关系；同角三角函数的关系．专题：计算题．分析：根据公式sin2α+cos2α=1列出关于未知数t的一元二次方程，然后根据根与系数的关系解答．解答：解：根据已知，得，即2=，∴3t2+5t﹣8=0，∴解得t1=1，t2=﹣，又∵＞0，即t＞0，∴t2=﹣不符合题意舍去，∴t所有可能值的和为1．故选C．点评：本题主要考查了同角三角函数的关系及根与系数的关系．解答此题的关键是熟练掌握同角三角函数的关系：sin2α+cos2α=1．6．（5分）满足（n2﹣n﹣1）n+2=1的整数n有几个（）A．4个B．3个C．2个D．1个考点：一元二次方程的解；零指数幂．专题：计算题．分析：因为1的任何次幂为1，﹣1的偶次幂为1，非0数的0次幂为1，所以应分三种情况讨论n 的值．解答：解：（1）n2﹣n﹣1=1，解得：n=2或n=﹣1；（2），解得：n=0；（3），解得：n=﹣2．故选A．点评：本题比较复杂，解答此题时要注意1的任何次幂为1，﹣1的偶次幂为1，非0数的0次幂为1，三种情况，不要漏解．7．（5分）如图，双曲线y=（x＞0）与矩形OABC的边BC，BA分别交于点E，F，且AF=BF，连接EF，则△OEF的面积为（）A．1.5 B．2C．2.5 D．3考点：反比例函数综合题．分析：设B（a，b），根据题意得F，由点F在双曲线上，得a×=2，即ab=4，E、B两点纵坐标相等，且E点在双曲线上，则E（，b），再根据S△OEF=S梯形OFBC﹣S△OEC ﹣S△FBE求解．解答：解：如图，设点B的坐标为（a，b），则点F的坐标为．∵点F在双曲线上，∴a×=2，解得ab=4，又∵点E在双曲线上，且纵坐标为b，所以点E的坐标为（，b），则S△OEF=S梯形OFBC﹣S△OEC﹣S△FBE，=×（+b）a﹣×b×﹣××（a﹣）=（ab+1﹣2）=．故选：A．点评：本题考查了反比例函数图象上点的性质，直角坐标系中三角形面积的表示方法．注意双曲线上点的横坐标与纵坐标的积为常数．8．（5分）若实数a，b满足，则a的取值范围是（）A．a≤﹣2 B．a≥4 C．a≤﹣2或a≥4 D．﹣2≤a≤4考点：根的判别式．分析：把看作是关于b的一元二次方程，由△≥0，得关于a的不等式，解不等式即可．解答：解：把看作是关于b的一元二次方程，因为b是实数，所以关于b的一元二次方程的判别式△≥0，即a2﹣4（a+2）≥0，a2﹣2a﹣8≥0，（a﹣4）（a+2）≥0，解得a≤﹣2或a≥4．故选C．点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．同时考查了一元二次不等式的解法．二、填空题（共6小题，每小题4分，共24分）9．（4分）若关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，且这三个根恰好可以作为一个三角形的三条边的长，则m的取值范围是3＜m≤4．考点：根与系数的关系；三角形三边关系．专题：计算题．分析：根据原方程可知x﹣2=0，和x2﹣4x+m=0，因为关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，所以x2﹣4x+m=0的根的判别式△＞0，然后再由三角形的三边关系来确定m的取值范围．解答：解：∵关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，∴①x﹣2=0，解得x1=2；②x2﹣4x+m=0，∴△=16﹣4m≥0，即m≤4，∴x 2=2+，x 3=2﹣，又∵这三个根恰好可以作为一个三角形的三条边的长，且最长边为x2，∴x1+x3＞x2；解得3＜m≤4，∴m的取值范围是3＜m≤4．故答案为：3＜m≤4．点评：本题主要考查了根与系数的关系、根的判别式及三角形的三边关系．解答此题时，需注意，三角形任意两边和大于第三边．10．（4分）已知：sinα﹣cosα=，则sinαcosα=（0＜α＜90°）考点：同角三角函数的关系．分析：对sinα﹣cosα=两边平方，然后根据sin2α+cos2α=1即可求解．解答：解：∵sinα﹣cosα=，∴（sinα﹣cosα）2=，∴sin2α﹣2sinαcosα+cos2α=，∵sin2α+cos2α=1∴2sinαcosα=1﹣=．∴sinαcosα=．点评：本题主要考查了同角的三角函数的关系，正确理解sin2α+cos2α=1是关键．11．（4分）双曲线y=（x＞0）与直线y=x在坐标系中的图象如图所示，点A、B在直线上AC、BD分别平行y轴，交曲线于C、D两点，若BD=2AC 则4OC2﹣OD2的值为6．考点：反比例函数综合题．分析：根据A，B两点在直线y=x上，分别设A，B两点的坐标为（a，a），（b，b），得到点C的坐标为（a，），点D的坐标为（b，），线段AC=a﹣，线段BD=b﹣，根据BD=2AC，有b﹣=2（a﹣），然后利用勾股定理进行计算求出4OC2﹣OD2的值．解答：解：设A（a，a），B（b，b），则C（a，），D（b，），AC=a﹣，BD=b﹣，∵BD=2AC，∴b﹣=2（a﹣），4OC2﹣OD2=4（a2+）﹣（b2+）=4[+2]﹣[+2]=4+8﹣4﹣2=6．故答案为：6．点评：本题考查的是反比例函数综合题，根据直线与反比例函数的解析式，设出点A，B的坐标后可以得到点C，D的坐标，运用勾股定理进行计算求出代数式的值．12．（4分）二次函数y=x2+bx+c的图象与x轴正方向交于A，B两点，与y轴正方向交于点C．已知，∠CAO=30°，则c=．考点：二次函数综合题．分析：首先利用根与系数的关系求得A，B两点横坐标之间的关系，再进一步结合已知，利用直角三角形的边角关系，把两点横坐标用c表示，由此联立方程解决问题．解答：解：如图，由题意知，点C的坐标为（0，c），OC=c．设A，B两点的坐标分别为（x1，0），（x2，0），则x1，x2是方程x2+bx+c=0的两根，由根与系数的关系得x1+x2=﹣b，x1x2=c，又∠CAO=30°，则；于是，，．由x1x2=9c2=c，得．故答案为：．点评：本题主要考查二次函数图象与坐标轴交点坐标特点、根与系数的关系以及直角三角形的边角关系解答问题．13．（4分）如图，AB是⊙O的直径，AB=10cm，M是半圆AB的一个三等分点，N是半圆AB的一个六等分点，P是直径AB上一动点，连接MP、NP，则MP+NP的最小值是cm．考点：轴对称-最短路线问题；圆心角、弧、弦的关系．专题：计算题．分析：作N关于AB的对称点N′，连接MN′交AB于点P，则点P即为所求的点，再根据M是半圆AB的一个三等分点，N是半圆AB的一个六等分点可求出∠MON′的值，再由勾股定理即可求出MN′的长．解答：解：作N关于AB的对称点N′，连接MN′交AB于点P，则点P即为所求的点，∵M是半圆AB的一个三等分点，N是半圆AB的一个六等分点，∴∠MOB==60°，∠BON′==30°，∴∠MON′=90°，∵AB=10cm，∴OM=ON′=5cm，∴MN′===5cm，即MP+NP的最小值是cm．故答案为：5．点评：本题考查的是最短路线问题及圆心角、弧、弦的关系，根据M是半圆AB的一个三等分点，N是半圆AB的一个六等分点，求出∠MON′=90°是解答此题的关键．14．（4分）函数y=x+（x＞0）的最小值为2．考点：函数最值问题．专题：计算题．分析：注意到两项的积为定值，且为正数，故考虑利用基本不等式即可解决．解答：解：∵y=x+≥2=2，当且仅当x=，即x=1时，取等号．故函数y=x+（x＞0）的最小值为2．故答案为：2．点评：此题考查了函数的最值问题，解答本题的关键是掌握不等式的基本性质，及a+b≥2，难度一般．三、解答题（本大题共5小题，共56分，解答应写出必要的过程或演算步骤）15．（10分）已知△ABC中，AD是BC边上的高，∠C=32°，若AD2=BD•CD，求∠ABC的度数．考点：相似三角形的判定与性质．专题：分类讨论．分析：根据已知可得到△BDA∽△ADC，注意∠C可以是锐角也可是钝角，故应该分情况进行分析，从而确定∠BCA度数．解答：解：分两种情况：（1）当B、C分别位于点D的两侧时（如图1），∵AD2=BD•DC，AD是BC边上的高得，∴△ABD∽△CAD，∴∠B=∠DAC=90°﹣∠C=90°﹣32°=58°；（2）当B、C分别位于点D的同侧时（如图2），∵AD2=BD•DC，AD是BC边上的高得，∴△ABD∽△CAD，∴∠BAD=∠C=32°，∴∠ABC=∠BAD+∠ADB=32°+90°=122°．点评：本题考查的是相似三角形的判定与性质，解答此题时要注意分类讨论，不要漏解．16．（10分）如图，身高1.5米的小亮AB在路灯CD下的影长为1米，当小亮向远离路灯的方向走出1米后，影长变成了2米．求路灯CD的高．考点：相似三角形的应用．专题：计算题．分析：运用已知条件得出AB∥CD，A′B′∥CD，进而得出相应比例式，得出关于BD，CD的方程，进而求出CD．解答：解：根据题意可得：AB∥CD，A′B′∥CD，∵AB=1.5米，BB′=1米，B′E=2米，∴，∴，①∴，∴，②由①得：2CD﹣1.5BD=4.5，③由②得：CD﹣1.5BD=1.5，④③﹣④得：CD=3米，答：路灯CD的高为3米．点评：此题主要考查了相似三角形的性质，利用对应变成比例得出比例式，进而求出方程的解是解决问题的关键．17．（10分）如图，已知圆内接四边形ABCD的对角线AC、BD交于点N，点M在对角线BD上，且满足∠BAM=∠DAN，∠BCM=∠DCN．求证：（1）M为BD的中点；（2）．考点：圆内接四边形的性质；圆心角、弧、弦的关系；圆周角定理；相似三角形的判定与性质．专题：证明题．分析：（1）要证M为BD的中点，即证BM=DM，由∠BAM=∠DAN，∠BCM=∠DCN，及圆周角的性质易证明△BAM∽△CBM，△DAM∽△CDM得出比例的乘积形式，可证明BM=DM；（2）欲证，可以通过平行线的性质证明，需要延长AM交圆于点P，连接CP，证明PC∥BD，得出比例式，相应解决MP=CM的问题即可．解答：证明：（1）根据同弧所对的圆周角相等，得∠DAN=∠DBC，∠DCN=∠DBA．又∵∠DAN=∠BAM，∠BCM=∠DCN，∴∠BAM=∠MBC，∠ABM=∠BCM．∴△BAM∽△CBM，∴，即BM2=AM•CM．①又∠DCM=∠DCN+∠NCM=∠BCM+∠NCM=∠ACB=∠ADB，∠DAM=∠MAC+∠DAN=∠MAC+∠BAM=∠BAC=∠CDM，∴△DAM∽△CDM，则，即DM2=AM•CM．②由式①、②得BM=DM，即M为BD的中点．（2）如图，延长AM交圆于点P，连接CP．∴∠BCP=∠PAB=∠DAC=∠DBC．∵PC∥BD，∴．③又∵∠MCB=∠DCA=∠ABD，∠DBC=∠PCB，∴∠ABC=∠MCP．而∠ABC=∠APC，则∠APC=∠MCP，有MP=CM．④由式③、④得．点评：本题考查了相似三角形的性质，圆周角的性质，是一道较难的题目．18．（12分）已知在△ABC中，∠ACB=90°，AC=BC=4，现将一块边长足够大的直角三角板的直角顶点置于AB的中点O，两直角边分别经过点B、C，然后将三角板绕点O按顺时针方向旋转一个角度α（0°＜α＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK 是旋转过程中三角板与△ABC的重叠部分（如图所示）．那么，在上述旋转过程中：（1）线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？证明你发现的结论；（2）连接HK，设BH=x．①当△CHK的面积为时，求出x的值．②试问△OHK的面积是否存在最小值，若存在，求出此时x的值，若不存在，请说明理由．考点：旋转的性质；二次函数的最值；全等三角形的判定与性质．专题：代数几何综合题．分析：（1）连接OC，可以证得：△COK≌△BOH，根据S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=S△ABC即可证得：四边形CHOK的面积始终保持不变；（2）①BC=4，CH=4﹣x，三角形的面积公式可以得到：CH•CK=，即（4﹣x）x=3，从而求得x的值；②设△OKH的面积为S，根据三角形的面积公式，即可得到关于x的函数关系式，然后根据函数的性质即可求解．解答：解：（1）在旋转过程中，BH=CK，四边形CHOK的面积始终保持不变，其值为△ABC面积的一半．理由如下：连接OC∵△ABC为等腰直角三角形，O为斜边AB的中点，CO⊥AB∴∠OCK=∠B=45°，CO=OB，又∵∠COK与∠BOH均为旋转角，∴∠COK=∠BOH=α∴△COK≌△BOH∴BH=CK，S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=S△ABC=4．（2）①由（1）知CK=BH=x，∵BC=4，∴CH=4﹣x，根据题意，得CH•CK=，即（4﹣x）x=3，解这个方程得x1=1，x2=3，此两根满足条件：0＜x＜4所以当△CKH的面积为时，x的取值是1或3；②设△OKH的面积为S，由（1）知四边形CHOK的面积为4，于是得关系式：S=4﹣S△CKH=4﹣x（4﹣x）=（x2﹣4x）+4=（x﹣2）2+2当x=2时，函数S有最小值2，∵x=2时，满足条件0＜x＜4，∴△OKH的面积存在最小值，此时x的值是2．点评：本题考查了三角形全等的判定与性质，以及二次函数的性质，正确列出函数解析式是解题的关键．19．（14分）已知二次函数y=x2+bx﹣c的图象经过两点P（1，a），Q（2，10a）．（1）如果a，b，c都是整数，且c＜b＜8a，求a，b，c的值．（2）设二次函数y=x2+bx﹣c的图象与x轴的交点为A、B，与y轴的交点为C．如果关于x的方程x2+bx﹣c=0的两个根都是整数，求△ABC的面积．考点：二次函数综合题．分析：（1）代入两点坐标，求得b、c（用a表示），再由已知c＜b＜8a，联立不等式组求得a、b、c的值；（2）设出程x2+bx﹣c=0的两个根，根据根与系数的关系与因式分解求得两根，得出函数解析式，进一步求得图象与x、y轴的交点A、B、C三点解答问题．解答：解：点P（1，a）、Q（2，10a）在二次函数y=x2+bx﹣c的图象上，故1+b﹣c=a，4+2b﹣c=10a，解得b=9a﹣3，c=8a﹣2；（1）由c＜b＜8a知，解得1＜a＜3，又a为整数，所以a=2，b=9a﹣3=15，c=8a﹣2=14；（2）设m，n是方程的两个整数根，且m≤n．由根与系数的关系可得m+n=﹣b=3﹣9a，mn=﹣c=2﹣8a，消去a，得9mn﹣8（m+n）=﹣6，两边同时乘以9，得81mn﹣72（m+n）=﹣54，分解因式，得（9m﹣8）（9n﹣8）=10．所以或或或，解得或或或；又∵m，n是整数，所以后面三组解舍去，故m=1，n=2．因此，b=﹣（m+n）=﹣3，c=﹣mn=﹣2，二次函数的解析式为y=x2﹣3x+2．易求得点A、B的坐标为（1，0）和（2，0），点C的坐标为（0，2），所以△ABC的面积为．点评：此题主要考查二次函数图象上点的坐标特点、根与系数的关系、不等式组、以及三角形的面积计算公式．。

浙江省杭州市2011年中考数学仿真模拟试卷10考生须知：1、本试卷分试题卷和答题卷两部分，满分120分，考试时间100分钟．2、答题前，必须在答题卷的密封区内填写校名、姓名和准考证号．3 、所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应．4 、考试结束后，上交试题卷和答题卷．试 题 卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内。

注意可以用多种不同的方法来选取正确答案。

1．北京时间2011年3月11日，日本发生了9.0级大地震，地震发生后， 中国红十字会一直与日本红十字会保持沟通，密切关注灾情发展。

截至目前，中国红十字会已经累计向日本红十字会提供600万元人民币的人道援助。

这里的数据“600万元”用科学计数法表示为（ ▲ ）（第1题）A ． 4610⨯元B ． 5610⨯元C ．6610⨯元D ．7610⨯元2. 若a =，5b =，则a b 、两数的关系是（ ▲ ）A 、a b =B 、5a b =C 、a b 、互为相反数D 、a b 、互为倒数 3. 公务员行政能力测试中有一类图形规律题，可以运用我们初中数学中的图形变换再结 合变化规律来解决，下面一题问号格内的图形应该是（ ▲ ）（第3题）4. 某市2008年4月的一周中每天最低气温如下：13，11，7，12，13，13，12， 则在这一周中，最低气温的众数和中位数分别是( ▲ )A. 13和11B. 12和13C. 11和12D. 13和125．若有甲、乙两支水平相当的NBA 球队需进行总决赛，一共需要打7场，前4场2比2，最后三场比赛，规定三局两胜者为胜方，如果在第一次比赛中甲获胜，这时乙最终取胜的可能性有多大？（不考虑主场优势）（ ▲ ） A ．21 B ．31 C ．41 D ． 156. 如图，△ABC 内接于⊙O ，∠C=45°，AB=2，则⊙O 的半径为( ▲ )A ．1B ．22C ．2D ．2（第6题）（第7题）7. 如图，小亮同学在晚上由路灯A 走向路灯B ，当他走到点P 时，发现他的身影顶部正好接触路灯B 的底部，这时他离路灯A 25米，离路灯B 5米，如果小亮的身高为1.6米，那么路灯高度为 ( ▲ )A ．6.4米B ． 8米C ．9.6米D ． 11.2米8. 如图，圆内接四边形ABCD 是由四个全等的等腰梯形组成，AD 是⊙O 的直径，则∠BEC 的度数为( ▲ ) A ．15° B ．30° C ．45° D ．60°（第9题）9．如图，直线l 和双曲线k y x=（0k >）交于A 、B 两点，P 是线段AB 上的点（不与A 、B重合），过点A 、B 、P 分别向x 轴作垂线，垂足分别为C 、D 、E ，连接OA 、OB 、OP ，设△AOC 的面积为1S 、△BOD 的面积为2S 、△POE 的面积为3S ，则 ( ▲ ) A ．123S S S << B ．123S S S >> C ． 123S S S => D ． 123S S S =<10．如图，点C 、D 是以线段AB 为公共弦的两条圆弧的中点，AB =4，点E 、F 分别是线段CD ，AB 上的动点，设AF =x ，AE 2－FE 2=y ，则能表示y 与x 的函数关系的图象是( ▲ )二. 认真填一填（本题有6个小题，每小题4分，共24分）A ．(第8题)要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案. 11．分解因式：x x 43-= ▲12．已知函数y 1=2x-5，y 2= -2x +15，如果y 1＜y 2 ，则x 的取值范围是 ▲ 13．如图，相离的两个圆⊙O 1和⊙O 2在直线l 的同侧。

自主招生模拟练习（2）1、已知向量11(0,1),(),),(1,1)2222a b c xa yb zc ==--=-++=则222x y z ++ 的最小值为__________. 解：由(1,1)xa yb zc ++=得1)122211222y z y z y z y z x x ⎧⎧-+=--=⎪⎪⎪⎪⎨⎨+⎪⎪--=-=⎪⎪⎩⎩， 由于222222()()2y z y z x y z x ++-++=+，可以用换元法的思想，看成关于x ，y + z ，y - z三个变量，变形2(1)y z y z x ⎧-=-⎪⎨⎪+=-⎩，代入222222()()2y z y z x y z x ++-++=+222228242(1)343()3333x x x x x =+-+=-+=-+，答案B2、在正四棱锥P-ABCD 中，M 、N 分别为PA 、PB 的中点，且侧面与底面所成二面角DM 与AN 所成角的余弦为______.[分析]本题有许多条件，可以用“求解法”，即假设题中的一部分要素为已知，利用这些条件来确定其余的要素。

本题中可假设底面边长为已知（不妨设为2），利用侧面与底面所成二面角可确定其他要素，如正四棱锥的高等。

然后我们用两种方法，一种是建立坐标系，另一种是平移其中一条线段与另一条在一起.解法一：如图，设底面边长为2，则由侧面与底面所成二面角的正切为得高为如图建立坐标系，则A (1，-1，0)，B (1，1，0)，C (-1，1，0)，D (-1，-1，0)，P (0，0，则11112(,,),(,)222222M N -，3113(,,(,,)222222D M AN =-=- 。

设所成的角为θ，则1cos 6D M A N D M A Nθ==.解法二：如图，设底面边长为2。

平移DM 与AN 在一起。

即M 移到N ，D 移到CD 的中点Q 。

于是QN = DM = AN 。

而P A = PB= AB = 2，所以QN = AN =而AQ =容易算出等腰ΔAQN 的顶角1cos 6A N Q ∠=。

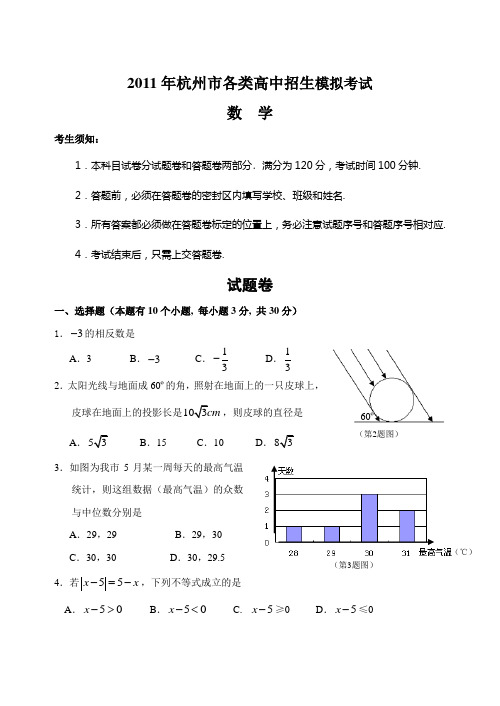
（℃）（第3题图）60º（第2题图）2011年杭州市各类高中招生模拟考试数 学考生须知：1．本科目试卷分试题卷和答题卷两部分．满分为120分，考试时间100分钟. 2．答题前，必须在答题卷的密封区内填写学校、班级和姓名.3．所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应. 4．考试结束后，只需上交答题卷.试题卷一、选择题（本题有10个小题, 每小题3分, 共30分） 1．3-的相反数是 A ．3B ．3-C ．13-D ．132．太阳光线与地面成60º的角，照射在地面上的一只皮球上，皮球在地面上的投影长是，则皮球的直径是 A． B ．15 C ．10 D．3．如图为我市5月某一周每天的最高气温统计，则这组数据（最高气温）的众数与中位数分别是 A ．29，29B ．29，30C ．30，30D ．30，29.54．若55x x -=-，下列不等式成立的是A ．50x ->B ．50x -<C . 5x -≥0D ．5x -≤0（第6题图）5．连续掷两次骰子，出现点数之和等于4的概率为 A ．136 B ．118 C ．112D ．196．如图，BD 是⊙O 的直径，∠CBD =30，则∠A 的度数为 A ．30 B ．45 C ．60 D ．757．小明用一个半径为5cm ，面积为15π2cm 的扇形纸片，制作成一个圆锥的侧面（接缝处不重叠），那么这个圆锥的底面半径为 A ．3cmB ．4cmC ．5cmD ．15cm8．如图，ABC △和的DEF △是等腰直角三角形，90C F ∠=∠=，24AB DE ==，．点B 与点D 重合，点A B D E ，（），在同一条直线上，将ABC △沿D E →方向平移，至点A 与点E 重合时停止．设点B D ，之间的距离为x ，ABC △与DEF △重叠部分的面积为y ，则准确反映y 与x 之间对应关系的图象是9．已知二次函数2y ax bx c =++中，其函数y 与自变量x 之间的部分对应值如下表所示：x… 0 1 2 3 … y…5212…（第11题图）O PBABCAE 1 E 2 E 3D 4D 1D 2D 3（第10题图）点A （1x ，1y ）、B （2x ，2y ）在函数的图象上，则当101x <<，223x <<时，1y 与2y 的大小关系正确的是 A ．1y ≥2yB ．12y y >C ．12y y <D ．1y ≤2y10．如图，已知Rt ABC △，1D 是斜边AB 的中点，过1D 作11D E AC ⊥于E 1，连结1BE 交1CD 于2D ；过2D 作22D E AC ⊥于2E ，连结2BE 交1CD 于3D ；过3D 作33D E AC ⊥于3E ，…，如此继续，可以依次得到点45D D ，，…，n D ，分别记112233BD E BD E BD E △，△，△，…，n n BD E △的面积为123S S S ，，，…n S ．则A ．n S =14n ABC S △B ．n S =13n +ABC S △ C ．n S =()121n +ABC S △ D ．n S =()211n +ABC S △二、填空题 （本题有6个小题, 每小题4分, 共24分）11．如图，⊙O 的半径OA =10cm ，弦AB =16cm ，P 为AB 上一动点，则点P 到圆心O 的最短距离为 cm ．12．在创建国家生态园林城市活动中，某市园林部门为扩大城市的绿化面积，进行了大量的树木移载．下表记录的是在相同的条件下移栽某种幼树的棵数与成活棵数：请依此估计这种幼树成活的概率是 ．（结果用小数表示，精确到0.1） 13．有八个球编号是①到⑧，其中有六个球一样重，另外两个球都轻1克，为了找出这两个球，用天平称了三次，结果如下：第一次①+②比③+④重，第二次⑤+⑥比⑦+⑧轻，移栽棵数100 1000 10000 成活棵数899109008（第15题图）A EC AB ADAO A（第16题图）FD G CFEB AHO （第14题图）第三次①+③+⑤和②+④+⑧一样重．那么，这两个轻球的编号是 ．14．如图，任意一个凸四边形ABCD ，E 、F 、G 、H 分别是各边的中点，图中阴影部分的两块面积之和是四边形ABCD 的面积的 ．15．如图是瑞典人科赫（Koch ）在1906年构造的能够描述雪花形状的科赫雪花图案．图形的作法是，从一个正三角形开始，把每条边分成三等份，然后以各边的中间长度为底边．分别向外作正三角形，再把“底边”线段抹掉．反复进行这一过程，就会得到一个“雪花”样子的曲线．这是一个极有特色的图形：在图形不断变换的过程中，它的周长趋于无穷大，而其面积却趋于定值．如果假定原正三角形边长为a ，则可算出下图每步变换后科赫雪花的周长：1C =3a ，2C = ，3C = ，…，则n C = ．16．如图，矩形纸片ABCD ，点E 是AB 上一点，且BE ∶EA =5∶3，EC=BCE 沿折痕EC 向上翻折，若点B 恰好落在AD 边上，设这个点为F ，则（1）AB = ，BC = ；（2）若⊙O 内切于以F 、E 、B 、C 为顶点的四边形，则⊙O 的面积= ． 三、解答题（本题有8个小题，共66分） 17. （本小题满分6分） （1）计算：01(π4)2---；（2）解不等式2335x --≤12x+．18．（本小题满分6分）一个几何体的三视图如图所示，它的俯视图为菱形．请写出该几何体的形状，并根据图中所给的数据求出它的侧面积和体积．主视图俯视图左视图（第18题图）19．（本小题满分6分）在数学学习中，及时对知识进行归纳和整理是完善知识结构的重要方法．善于学习的小明在学习了一次方程（组）、一元一次不等式和一次函数后，把相关知识归纳整理如下：（1①；② ；③ ；④ ；（2）如果点C 的坐标为（1，3），那么不等式kx b +≤11k x b +的解集是 ． 20．（本小题满分8分）已知A ，B 两点在直线l 的同侧，试用直尺（没有刻度）和圆规，在l 上找两点C 和D （CD 的长度为定值a ），使得AC +CD +DB 最短．（不要求写画法）1 （第19题图）一次函数与方程的关系一次函数与不等式的关系Bl（第20题图）21．(本小题满分8分) 某中学为促进课堂教学，提高教学质量，对九年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了如下图表，请你根据图表中提供的信息，解答下列问题． （1）请把三个图表中的空缺部分都补充完整；（2）你最喜欢以上哪一种教学方式或另外的教学方式，请提出你的建议，并简要说明理由（字数在20字以内）．25%编号410%编号122．（本小题满分10分）如图，以△AOD的三边为边，在AD的同侧作三个等边三角形△AED、△BOD、△AOF，请回答下列问题并说明理由：（1）四边形OBEF是什么四边形？（2）当△AOD满足什么条件时，四边形OBEF是菱形？是矩形？（3）当△AOD满足什么条件时，以O、B、E、F为顶点的四边形不存在？OA FD EB（第22题图）23．（本小题满分10分）随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点．抽样调查显示，截止2009年底某市汽车拥有量为14.4万辆．己知2007年底该市汽车拥有量为10万辆．（1）求2007年底至2009年底该市汽车拥有量的年平均增长率？（2）为保护城市环境，要求我市到2011年底汽车拥有量不超过15.464万辆，据估计从2009年底起，此后每年报废的汽车数量是上年底汽车拥有量的10％，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）24．(本小题满分12分) 如图，在平面直角坐标系中，已知点A 坐标为（2，4），直线2=x 与x 轴相交于点B ，连结OA ，抛物线2x y =从点O 沿OA 方向平移，与直线2=x 交于点P ，顶点M 到A 点时停止移动． （1）求线段OA 所在直线的函数解析式； （2）设抛物线顶点M 的横坐标为m ，①用m 的代数式表示点P 的坐标； ②当m 为何值时，线段PB 最短；（3）当线段PB 最短时，相应的抛物线上是否存在点Q ，使△QMA 的面积与△PMA 的面积相等，若存在，请求出点Q 的坐标；若不存在，请说明理由．数学参考解答和评分标准一、选择题(每题3分,共30分)二、填空题(每题4分,共24分) 11. 6， 12. 0.9， 13. ④⑤， 14.12， 15. 2C =433a ；3C =24()33a ；n C =14()33n a -，（1+1+2分） 16. AB =24，BC =30，⊙O 的面积=100π．（1+1+2分）三.解答题(共66分)17.（6分）解:（1）原式＝1212-+ ……………………1+1+1分 ＝12-…………………………1分（2）3046x -+≤55x + …………………………1分x ≤21- …………………………1分18.（6分）解：该几何体的形状是直四棱柱(答直棱柱，四棱柱，棱柱也给2分)． ………………………2分由三视图知，棱柱底面菱形的对角线长分别为4cm ，3cm ．∴ 菱形的边长为52cm ， ………………………1分棱柱的侧面积=52×8×4=80(cm 2)． ………………………2分 棱柱的体积=12×3×4×8=48(cm 3)． ………………………1分 19．（6分）解：（1）①0kx b +=；②11y k x b y kx b=+⎧⎨=+⎩；③kx b +>0；④kx b +<0；（1+1+1+1分）（2）如果点C 的坐标为（1，3），那么不等式kx b +≤11k x b +的解集是x ≥1．（2分）20．（8分）解：（1）过点A 作l 的垂线（尺规作图）； 在垂线上截取，找到对称点 A ′，（2分）（2）过点B 作l 的垂线（尺规作图），垂足为M ， 在l 上截取线段MN =a ； （2分）（3）分别以B 点为圆心，以a 长为半径画弧,以N 点为圆心，以BM 长为半径画弧，交于点B ′；（2（4）连接A ′B ′交l 于点C ，在l 上截取线段CD =a ．（2分）21.（8分）解：（1）100，0.5，0.15，50（每空0.5分）；（图略）（每图2分） （2）2分，无建议与理由得1分22.（10分）解：（1）平行四边形；（3分） （2）当OA =OD 时，四边形OBEF 为菱形；（2分） 当∠AOD =1500时，四边形OBEF 为矩形；（2分）（3）当∠AOD =600时，以O 、B 、E 、F 为顶点的四边形不存在．（3分） （每小题无理由只得1分）23．（10分）解：（1）设年平均增长率为x ，根据题意得： （1分）210(1)14.4x +=（2分） 解得：2.0=x （1分）答：年平均增长率为20%（1分）（2）设每年新增汽车数量最多不超过x 万辆，根据题意得： （1分） 2010年底汽车数量为14.490%x ⨯+ 2011年底汽车数量为(14.490%)90%x x ⨯+⨯+l∴ (14.490%)90%x x ⨯+⨯+15.464≤（2分） ∴ 2x ≤（1分）答：每年新增汽车数量最多不超过2万辆（1分）24.（12分 ）解：（1）设OA 所在直线的函数解析式为kx y =， ∵A （2，4），∴42=k , 2=∴k ,∴OA 所在直线的函数解析式为2y x =.………………………………………………2分 （2）①∵顶点M 的横坐标为m ，且在线段OA 上移动， ∴2y m =（0≤m ≤2）. ∴顶点M 的坐标为(m ,2m ).∴抛物线函数解析式为2()2y x m m =-+.∴当2=x 时，2(2)2y m m =-+224m m =-+（0≤m ≤2）. ∴点P 的坐标是（2，224m m -+） ……………………………………4分 ② ∵PB =224m m -+=2(1)3m -+， 又∵0≤m ≤2， ∴当1m =时，PB 最短. ……………………………………6分（3）当线段PB 最短时，此时抛物线的解析式为()212+-=x y .假设在抛物线上存在点Q ，使Q M A P M AS S =. 设点Q 的坐标为（x ，223x x -+）. ①当点Q 落在直线OA 的下方时，过P 作直线P C //AO ，交y 轴于点C ，∵3P B =，4AB =， ∴1A P =，∴1OC =，∴C 点的坐标是（0，1-）.∵点P 的坐标是（2，3），∴直线P C 的函数解析式为12-=x y . ∵Q M A P M AS S =，∴点Q 落在直线12-=x y 上. ∴223x x -+=21x -.解得122,2x x ==，即点Q （2，3）.∴点Q 与点P 重合.∴此时抛物线上不存在点Q ，使△QMA 与△AP M 的面积相等. ②当点Q 落在直线OA 的上方时，作点P 关于点A 的对称称点D ，过D 作直线DE //AO ，交y 轴于点E ，∵1A P =，∴1E OD A ==， ∴E 、D 的坐标分别是（0，1），（2，5），∴直线DE 函数解析式为12+=x y . ∵Q M A P M AS S =，∴点Q 落在直线12+=x y 上. ∴223x x -+=21x +.解得：12x =22x =代入12+=x y ，得15y =+25y =-∴此时抛物线上存在点(12Q ，()225,222--Q 使△QMA 与△PM A 的面积相等.综上所述，抛物线上存在点(12Q ，()225,222--Q 使△QMA 与△PM A 的面积相等.……………………………………………12分情感语录1.爱情合适就好，不要委屈将就，只要随意，彼此之间不要太大压力2.时间会把最正确的人带到你身边，在此之前，你要做的，是好好的照顾自己3.女人的眼泪是最无用的液体，但你让女人流泪说明你很无用4.总有一天，你会遇上那个人，陪你看日出，直到你的人生落幕5.最美的感动是我以为人去楼空的时候你依然在6.我莫名其妙的地笑了，原来只因为想到了你7.会离开的都是废品，能抢走的都是垃圾8.其实你不知道，如果可以，我愿意把整颗心都刻满你的名字9.女人谁不愿意青春永驻，但我愿意用来换一个疼我的你10.我们和好吧，我想和你拌嘴吵架，想闹小脾气，想为了你哭鼻子，我想你了11.如此情深，却难以启齿。

（℃）（第题图）º（第题图）年杭州市各类高中招生模拟考试数 学考生须知：．本科目试卷分试题卷和答题卷两部分．满分为分，考试时间分钟. ．答题前，必须在答题卷的密封区内填写学校、班级和姓名.．所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应. ．考试结束后，只需上交答题卷.试题卷一、选择题（本题有个小题, 每小题分, 共分） ．的相反数是 ．．．．．太阳光线与地面成º的角，照射在地面上的一只皮球上，皮球在地面上的投影长是，则皮球的直径是 ．． ． ．．如图为我市月某一周每天的最高气温统计，则这组数据（最高气温）的众数与中位数分别是 ．， ．，．， ．，．若，下列不等式成立的是 ．．.≥．≤．连续掷两次骰子，出现点数之和等于的概率为（第题图）． ． ． ．．如图，是⊙的直径，∠，则∠的度数为 ． ． ． ．．小明用一个半径为，面积为的扇形纸片，制作成一个圆锥的侧面（接缝处不重叠），那么这个圆锥的底面半径为 ．． ．．．如图，和的是等腰直角三角形，，．点与点重合，点在同一条直线上，将沿方向平移，至点与点重合时停止．设点之间的距离为，与重叠部分的面积为，则准确反映与之间对应关系的图象是．已知二次函数中，其函数与自变量之间的部分对应值如下表所示：… ………（第题图）（第题图）点（，）、（，）在函数的图象上，则当，时，与的大小关系正确的是 ．≥．． ．≤．如图，已知，是斜边的中点，过作于，连结交于；过作于，连结交于；过作于，…，如此继续，可以依次得到点，…，，分别记…，的面积为，…．则．．．．二、填空题 （本题有个小题, 每小题分, 共分）．如图，⊙的半径，弦，为上一动点， 则点到圆心的最短距离为 ．．在创建国家生态园林城市活动中，某市园林部门为扩大城市的绿化面积，进行了大量的树木移载．下表记录的是在相同的条件下移栽某种幼树的棵数与成活棵数： 请依此估计这种幼树成活的概率是 ．（结果用小数表示，精确到）．有八个球编号是①到⑧，其中有六个球一样重，另外两个球都轻克，为了找出这两个球，用天平称了三次，结果如下：第一次①②比③④重，第二次⑤⑥比⑦⑧轻，第三移栽棵数成活棵数（第题图）（第题图）（第题图）次①③⑤和②④⑧一样重．那么，这两个轻球的编号是 ．．如图，任意一个凸四边形，、、、分别是各边的中点，图中阴影部分的两块面积之和是四边形的面积的 ． ．如图是瑞典人科赫（）在年构造的能够描述雪花形状的科赫雪花图案．图形的作法是，从一个正三角形开始，把每条边分成三等份，然后以各边的中间长度为底边．分别向外作正三角形，再把“底边”线段抹掉．反复进行这一过程，就会得到一个“雪花”样子的曲线．这是一个极有特色的图形：在图形不断变换的过程中，它的周长趋于无穷大，而其面积却趋于定值．如果假定原正三角形边长为，则可算出下图每步变换后科赫雪花的周长：，，，…，则．．如图，矩形纸片，点是上一点，且∶∶，，把△沿折痕向上翻折，若点恰好落在边上，设这个点为，则（） ， ；（）若⊙内切于以、、、为顶点的四边形，则⊙的面积 ．三、解答题（本题有个小题，共分） . （本小题满分分） （）计算：；（）解不等式≤．．（本小题满分分）一个几何体的三视图如图所示，它的俯视图为菱形．请写出该几何体的形状，并根据图中所给的数据求出它的侧面积和体积．主视图俯视图 左视图（第题图）．（本小题满分分）在数学学习中，及时对知识进行归纳和整理是完善知识结构的重要方法．善于学习的小明在学习了一次方程（组）、一元一次不等式和一次函数后，把相关知识归纳整理如下：（）请你根据以上方框中的内容在下面数字序号后写出相应的结论：① ；② ；③ ；④ ；（）如果点的坐标为（，），那么不等式≤的解集是 ．．（本小题满分分）已知，两点在直线的同侧，试用直尺（没有刻度）和圆规，在上找两点和（的长度为定值），使得最短．（不要求写画法）（第题图）一次函数与方程的关系一次函数与不等式的关系（）一次函数的解析式就是一个二元一次方程（）点的横坐标是方程①的解；（）点的坐标中的的值是方程组（）函数的函数值大于时，自变量的取值范围就是不等式③的解集；（）函数的函数值小于时，自变量的取值范围就是不等式④的解集．（第题图）．(本小题满分分) 某中学为促进课堂教学，提高教学质量，对九年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了如下图表，请你根据图表中提供的信息，解答下列问题． （）请把三个图表中的空缺部分都补充完整；（）你最喜欢以上哪一种教学方式或另外的教学方式，请提出你的建议，并简要说明理由（字数在字以内）．．（本小题满分分）如图，以△的三边为边，在的同侧作三个等边三角形编号编号△、△、△，请回答下列问题并说明理由：（）四边形是什么四边形？（）当△满足什么条件时，四边形是菱形？是矩形？（）当△满足什么条件时，以、、、为顶点的四边形不存在？（第题图）．（本小题满分分）随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点．抽样调查显示，截止年底某市汽车拥有量为万辆．己知年底该市汽车拥有量为万辆．（）求年底至年底该市汽车拥有量的年平均增长率？（）为保护城市环境，要求我市到年底汽车拥有量不超过万辆，据估计从年底起，此后每年报废的汽车数量是上年底汽车拥有量的％，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）．(本小题满分分)如图，在平面直角坐标系中，已知点坐标为（，），直线与轴相交于点，连结，抛物线从点沿方向平移，与直线交于点，顶点到点时停止移动． （）求线段所在直线的函数解析式；（）设抛物线顶点的横坐标为，①用的代数式表示点的坐标； ②当为何值时，线段最短；（）当线段最短时，相应的抛物线上是否存在点，使△的面积与△的面积相等，若存在，请求出点的坐标；若不存在，请说明理由．数学参考解答和评分标准一、选择题(每题分,共分)二、填空题(每题分,共分).，.，.④⑤， .，.；；，（分）. ，，⊙的面积．（分）三.解答题(共分).（分）解:（）原式＝……………………分＝…………………………分（）≤…………………………分≤…………………………分.（分）解：该几何体的形状是直四棱柱(答直棱柱，四棱柱，棱柱也给分)．………………………分由三视图知，棱柱底面菱形的对角线长分别为，．∴菱形的边长为，………………………分棱柱的侧面积××()．………………………分棱柱的体积×××()．………………………分．（分）解：（）①；②；③>；④<；（分）（）如果点的坐标为（，），那么不等式≤的解集是≥．（分）在垂线上截取，找到对称点′，（分）（）过点作的垂线（尺规作图），垂足为，在上截取线段；（分）（）分别以点为圆心，以长为半径画弧,以点为圆心，以长为半径画弧，交于点′；（分）（）连接′′交于点，在上截取线段．（分）.（分）解：（），，，（每空分）；（图略）（每图分）（）分，无建议与理由得分.（分）解：（）平行四边形；（分）（）当时，四边形为菱形；（分）当∠时，四边形为矩形；（分）（）当∠时，以、、、为顶点的四边形不存在．（分）（每小题无理由只得分）．（分）解：（）设年平均增长率为，根据题意得：（分）（分）解得：（分）答：年平均增长率为（分）（）设每年新增汽车数量最多不超过万辆，根据题意得：（分）年底汽车数量为年底汽车数量为∴（分）∴（分）答：每年新增汽车数量最多不超过万辆（分）.（分）解：（）设所在直线的函数解析式为，∵（，），∴, ,∴所在直线的函数解析式为.………………………………………………分（）①∵顶点的横坐标为，且在线段上移动，∴（≤≤）.∴顶点的坐标为(,).∴抛物线函数解析式为.∴当时，（≤≤）.∴点的坐标是（，）……………………………………分②∵，又∵≤≤，∴当时，最短. ……………………………………分（）当线段最短时，此时抛物线的解析式为.假设在抛物线上存在点，使. 设点的坐标为（，）.①当点落在直线的下方时，过作直线，交轴于点，∵，，∴，∴，∴点的坐标是（，）.∵点的坐标是（，），∴直线的函数解析式为.∵，∴点落在直线上.∴.解得，即点（，）.∴点与点重合.∴此时抛物线上不存在点，使△与△的面积相等.②当点落在直线的上方时，作点关于点的对称称点，过作直线，交轴于点，∵，∴，∴、的坐标分别是（，），（，），∴直线函数解析式为.∵，∴点落在直线上.∴.解得：，.代入，得，.∴此时抛物线上存在点，使△与△的面积相等.综上所述，抛物线上存在点，使△与△的面积相等.……………………………………………分个人整理，仅供交流学习--------------------------------------------------------------------------------------------------------------------。

2011年浙江省温州中学高一自主招生物理试卷一、不定项选择题（每小题5分，共20分．在每小题给出的四个选项中，有的只有一个选顶符合要求，有的有多个选项符合要求，全部选对的得5分，选不全对的得3分，有选错或不选的得0分．）1．（5分）一锅沸腾的油，魔术师把手伸进去，一分钟、两分钟…再把手拿出来﹣﹣没事！对这一现象的分析正确的是（）A．这是不可能的，是伪科学B．这是不可能的，油在沸腾时温度不断升高C．这是可能的，一定是这种油的沸点很低D．这是可能的，一定是手上沾有水，水从油中吸收了热2．（5分）如图所示，水平桌面上有一装满水的烧杯和一个物块。

杯内水对杯底的压强为P1，烧杯对桌面的压强为P2．若将物块轻轻地放入烧杯中，则物块放入后（）A．P1增大，P2一定不变B．P l增大，P2可能增大C．P l不变，P2一定不变D．P1不变，P2可能增大3．（5分）质量分布不均的杆一端用铰链固接，在杆上某处悬挂一物块。

今用竖直向上的力作用在杆的另一端，缓慢地将杆从A位置拉至水平B位置的过程中（杆与铰链的摩擦不计），以下说法正确的是（）A．F大小不变B．F在变小C．F相对于铰链的力矩（力和力臂的乘积）不变D．F相对于铰链的力矩在变大4．（5分）如图所示，质量相同的甲、乙两人分别坐在两辆相同的小车上，两车置于水平光滑地面上关于中点对称的两侧，他们分别拉轻绳的一端进行拉车比赛。

裁判下令后，两人同时从静止开始，尽全力拉绳投入比赛。

比赛中手与绳子间不打滑。

则下列说法不正确的是（）A．若甲的力气比乙的大，甲先到达中点B．若甲的力气比乙的大，甲是加速前进，乙是减速前进C．不论谁的力气大，甲、乙两车均同时到达中点D．无论谁的力气大，甲、乙两车均是匀速前进二、填空题（按题目要求作答．每小题6分，共30分．）5．（6分）甲、乙、丙三幅图中，物块质量相等，均放在水平地面上，物块与地面间的滑动摩擦力均相同。

细线水平，滑轮质量不计，其余阻力不计。