周次 - 浙江省苍南中学--省一级重点中学

浙江省重点高中排行榜前32名(2023)浙江省重点高中排行榜前32名序号学校名称省份1浙江省镇海中学浙江省2杭州第二中学浙江省3杭州学军中学浙江省4杭州外国语学校浙江省5温州乐清市乐成寄宿中学浙江省6浙江省余姚中学浙江省7浙江省慈溪中学浙江省8浙江省诸暨中学浙江省9浙江省北仑中学浙江省10宁波市鄞州中学浙江省11浙江省萧山中学浙江省12金华市第一中学浙江省13舟山中学浙江省14宁波效实中学浙江省15金华市外国语学校浙江省16余杭高级中学浙江省17宁波市镇海蛟川书院浙江省18浙江省义乌中学浙江省19绍兴县鲁迅中学浙江省20浙江省春晖中学浙江省21浙江省温州中学浙江省22杭州高级中学浙江省23杭州第十四中学浙江省24浙江省宁海中学浙江省25嘉兴市第一中学浙江省26衢州第二中学浙江省27浙江省东阳中学浙江省28奉化中学浙江省29绍兴市第一中学浙江省30浙江省缙云中学浙江省31桐乡市高级中学浙江省32宁波中学浙江省注：以上高中排名源于网络，仅供参考，不代表本网站观点浙江省实力强的高中杭州第十一中学该高中创办于1904年，前身为贞文女学堂，是由中国人自己开办的最早的女学堂之一，也是杭城办学历史最悠久的百年名校之一。

悠久的历史与深厚的文化积淀，铸就了学校优秀的品质。

浙江省镇海中学浙江省镇海中学在1978年成为浙江省十三所重点中学之一，1981年被评为浙江省首批办好的十八所重点中学之一，1995年被评为第一所"浙江省一级重点中学"，2014年被授予"浙江省一级普通高中特色示范学校"称号。

从2022年开始，镇海中学取消保送生政策，实行统招和定向分配相结合的招生制度。

高中主要学什么?高中主要课程：1、文化课：语文、数学、外语(英语、日语、法语、德语、俄语或西班牙语)、历史、思想政治、地理、化学、物理、生物。

2、素质教育课：体育、美术、音乐、技术(信息技术及通用技术)。

高级中学是我国九年义务教育结束后更高等的教育机构，上承初中，下启大学，一般为三年制。

“美丽人生”特刊校园迷彩主 办二○○七年八月 (第一期)在2007级高一新生军训动员大会上的讲话苍南中学校长、党总支书记 仁英高中董事长杨道想尊敬的各位教官、县人武部和教育局领导，亲爱的老师、同学们： 大家下午好！今天，我们会聚绿荫草地，共同拉开了2007级高一新生军训活动的序幕。

首先，我谨代表苍南中学和仁英高中全体师生向前来学校承担军训任务的驻苍海军92773部队的各位官兵表示热烈的欢迎，并致以崇高的敬意！向刚刚踏进苍南中学和仁英高中校门的新同学和新班主任表示热烈的欢迎和衷心的祝贺，祝贺你们成为光荣的苍中人、仁高人！同学们，我们苍南中学系浙江省一级重点中学，省文明学校、省首批现代教育技术实验学校、省科研兴校200强学校，温州市“花园式单位”、温州市高中“校本教研”示范校、温州市新课程“样本校”。

仁英高中系苍南中学兴办的国有民办学校，她与苍中同根同源，共享优秀教育资源，并在苍中的先进办学思想滋润下茁壮成长。

2007年是我们苍南中学和仁英高中分别创建省级文明单位和县级文明单位的关键之年。

近年来，我们紧紧围绕“创文明，求和谐，争一流，铸名校”的行动目标，认真实施“美丽人生”德育工程和“科研兴师，名师强校”的发展战略，积极开展教育教学活动，取得了显著的成绩，如苍南中学2007年高考重点上线314人，上线率为47.0%；二本上线516人，上线率为77.5%；本科上线636人，上线率为95.6%，名列温州市第三。

仁英高中2007年高考重点上线8人，上线率为3.0%；二本上线44人，上线率为16.2%；本科上线117人，上线率为43.0%，总上线率为93.4%，名列苍南县普通高中前茅。

学校还先后被评为全国优秀科研校、全国优秀特色校、省2002-2005年度群众体育先进单位、温州市德育特色学校、温州市学生军训工作先进单位、温州市教师教育先进单位、温州市语言文字规范化示范校。

仁英高中今年被评为温州市德育工作先进集体。

2023-2024学年浙江省温州市部分重点中学高一（上）期中数学试卷一、选择题1．已知集合A ＝{x |2x ﹣7＞0}，B ＝{2，3，4，5}，则A ∩B ＝（ ） A ．{3}B ．{4，5}C ．{3，4}D ．{3，4，5}2．若a ，b 为实数，则“a 2+b 2＝0”是“ab ＝0”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．已知函数f （x ）={2x −1，x ≥1|x +1|，x ＜1，若f （a ）＝2，则a 的所有可能值为（ ）A ．32B ．1，32C ．−3，32D ．−3，1，324．若幂函数f （x ）的图象经过点（√2，12），则下列判断正确的是（ ） A ．f （x ）在（0，+∞）上为增函数 B ．方程f （x ）＝4的实根为±2 C ．f （x ）的值域为（0，1）D ．f （x ）为偶函数5．若正数x ，y 满足xy ＝2，则3x •9y 的最小值为（ ） A ．27B ．81C ．6D ．96．若不等式ax 2﹣x ﹣c ＞0的解集为{x |﹣3＜x ＜2}，则函数y ＝ax 2+x ﹣a 的零点为（ ） A ．（3，0）和（﹣2，0） B ．（﹣3，0）和（2，0）C ．2和﹣3D ．﹣2和37．已知f （x ）={x 2−2tx +t 2，x ≤0x +1x+t ，x ＞0，若f （0）是f （x ）的最小值，则t 的取值范围为（ ） A ．[﹣1，2] B ．[﹣1，0] C ．[1，2] D ．[0，2]8．实数a ，b ，c 满足a 2＝2a +c ﹣b ﹣1且a +b 2+1＝0，则下列关系成立的是（ ） A ．b ＞a ≥c B ．c ＞a ＞bC ．b ＞c ≥aD ．c ＞b ＞a二、多项选择题9．下列命题为真命题的为（ ） A ．∀x ∈R ，x 2+x +1＞0B ．当ac ＞0时，∃x ∈R ，ax 2+bx ﹣c ＝0C ．|x ﹣y |＝|x |+|y |成立的充要条件是xy ≥0D ．设a ，b ∈R ，则“a ≠0”是“ab ≠0”的必要不充分条件10．已知x ，y 是正数，且2x +y ＝1，下列叙述正确的是（ ） A ．2xy 最大值为14B ．4x 2+y 2的最小值为12C ．x （x +y ）最大值为14D ．1x+1y最小值为3+2√211．下列说法正确的是（ ）A ．函数f （x ）的值域是[﹣2，2]，则函数f （x +1）的值域为[﹣3，1]B ．既是奇函数又是偶函数的函数只有一个C ．若A ∪B ＝B ，则A ∩B ＝AD ．函数f （x ）的定义域是[﹣2，2]，则函数f （x +1）的定义域为[﹣3，1]12．数学上，高斯符号（Gauss mark ）是指对取整符号和取小符号的统称，用于数论等领域．定义在数学特别是数论领域中，有时需要略去一个实数的小数部分只研究它的整数部分，或需要略去整数部分研究小数部分，因而引入高斯符号．设x ∈R ，用[x ]表示不超过x 的最大整数．比如： [1]＝1，[0]＝0，[﹣1]＝﹣1，[﹣1.2]＝﹣2，[1.3]＝1…，已知函数f(x)=[x]x(x ＞0)，则下列说法不正确的是（ ）A ．f （x ）的值域为[0，1）B ．f （x ）在（1，+∞）为减函数C ．方程f(x)=12无实根D ．方程f(x)=712仅有一个实根 三、填空题13．函数f(x)=√−x 2+2x +3的定义域为 ．14．已知函数f （x ）＝mx 2+nx +2（m ，n ∈R ）是定义在[2m ，m +3]上的偶函数，则函数g （x ）＝f （x ）+2x 在[﹣2，2]上的最小值为 ．15．股票是股份公司发给股东证明其所入股份的一种有价证券，它可以作为买卖对象和抵押品，是资金市场主要的长期信用工具之一．股票在公开市场交易时可涨可跌，在我国上海证券交易所交易的主板股票每个交易日上涨和下跌都不超过10%，当日上涨10%称为涨停，当日下跌10%称为跌停．某日贵州茅台每股的价格是1500元，若贵州茅台在1500元的价格上先涨停2天再跌停2天，则4天后每股的价格是 元．16．设y ＝f （x ）是定义在R 上的函数，对任意的x ∈R ，恒有f （x ）+f （﹣x ）＝x 2成立，g(x)=f(x)−x 22，若y ＝f （x ）在（﹣∞，0]上单调递增，且f （2﹣a ）﹣f （a ）≥2﹣2a ，则实数a 的取值范围是 ． 四、解答题17．（1）计算：(235)0+2−2×(214)−12−(0.01)0.5；（2）若实数a满足a 12+a−12=3，求a+a﹣1的值．18．已知函数f(x)=x+4x．（1）证明：f（x）在[2，+∞）为增函数；（2）求f（x）在[1，4]上的值域．19．在①A∪B＝B；②“x∈A”是“x∈B”的充分不必要条件；③A∩B＝∅这三个条件中任选一个，补充到本题第（2）问的横线处，求解下列问题．问题：已知集合A＝{x|a﹣1≤x≤2a+1}，B＝{x|﹣1≤x≤3}．（1）当a＝2时，求A∪B；A∩（∁R B）；（2）若______，求实数a的取值范围．20．设函数f（x）＝a•2x﹣2﹣x（a∈R）．（1）若函数y＝f（x）为奇函数，求方程f(x)+32=0的实根；（2）若函数h（x）＝f（x）+4x+2﹣x在x∈[0，1]的最大值为﹣2，求实数a的值．21．美国对中国芯片的技术封锁激发了中国“芯”的研究热潮．某公司研发的A，B两种芯片都已经获得成功．该公司研发芯片已经耗费资金2千万元，现在准备投入资金进行生产．经市场调查与预测，生产A芯片的毛收入与投入的资金成正比，已知每投入1千万元，公司获得毛收入0.25千万元；生产B芯片的毛收入y（千万元）与投入的资金x（千万元）的函数关系为y＝kx a（x＞0），其图像如图所示．（1）试分别求出生产A，B两种芯片的毛收入y（千万元）与投入资金x（千万元）的函数关系式；（2）现在公司准备投入40千万元资金同时生产A，B两种芯片，求可以获得的最大利润是多少．22．若函数y＝f（x）自变量的取值区间为[a，b]时，函数值的取值区间恰为[2b ，2a]，就称区间[a，b]为y＝f（x）的一个“和谐区间”．已知函数g（x）是定义在R上的奇函数，当x∈（0，+∞）时，g（x）＝﹣x+3．（1）求g（x）的解析式；（2）求函数g（x）在（0，+∞）内的“和谐区间”；（3）若以函数g（x）在定义域内所有“和谐区间”上的图象作为函数y＝h（x）的图象，是否存在实数m，使集合{（x，y）|y＝h（x）}∩{（x，y）|y＝x2+m}恰含有2个元素．若存在，求出实数m的取值集合；若不存在，说明理由．2023-2024学年浙江省温州市部分重点中学高一（上）期中数学试卷参考答案与试题解析一、选择题1．已知集合A ＝{x |2x ﹣7＞0}，B ＝{2，3，4，5}，则A ∩B ＝（ ） A ．{3}B ．{4，5}C ．{3，4}D ．{3，4，5}解：A ＝{x |2x ﹣7＞0}={x|x ＞72}，B ＝{2，3，4，5}，则A ∩B ＝{4，5}． 故选：B ．2．若a ，b 为实数，则“a 2+b 2＝0”是“ab ＝0”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解：由a 2+b 2＝0，可得a ＝0，b ＝0， 由ab ＝0，可得a ＝0或b ＝0，故由a 2+b 2＝0可推出ab ＝0，所以“a 2+b 2＝0”是“ab ＝0”的充分条件， 由ab ＝0推不出a 2+b 2＝0，所以“a 2+b 2＝0”是“ab ＝0”的不必要条件， 综上，“a 2+b 2＝0”是“ab ＝0”的充分不必要条件， 故选：A ． 3．已知函数f （x ）={2x −1，x ≥1|x +1|，x ＜1，若f （a ）＝2，则a 的所有可能值为（ ）A ．32B ．1，32C ．−3，32D ．−3，1，32解：当a ≥1时，则有2a ﹣1＝2，解得a =32； 当a ＜1时，则有|a +1|＝2，解得a ＝﹣3， 综上，a =32或a ＝﹣3． 故选：C ．4．若幂函数f （x ）的图象经过点（√2，12），则下列判断正确的是（ ）A ．f （x ）在（0，+∞）上为增函数B ．方程f （x ）＝4的实根为±2C ．f （x ）的值域为（0，1）D ．f （x ）为偶函数解：由题意可设，幂函数f （x ）＝x α，f （x ）的图象经过点（√2，12），则√2α=12，解得α＝﹣2， 故f （x ）＝x ﹣2，f （x ）在（0，+∞）上为减函数，故A 错误； f （x ）＝4，则x ﹣2＝4，解得x =±12，故B 错误；f （x ）的值域为（0，+∞），故C 错误；f （﹣x ）＝f （x ）＝x ﹣2，故f （x ）为偶函数，故D 正确．故选：D ．5．若正数x ，y 满足xy ＝2，则3x •9y 的最小值为（ ） A ．27B ．81C ．6D ．9解：因为正数x ，y 满足xy ＝2，所以x +2y ≥2√2xy =4，当且仅当x ＝2y 且xy ＝2，即y ＝1，x ＝2时取等号， 则3x •9y ＝3x +2y ≥34＝81． 故选：B ．6．若不等式ax 2﹣x ﹣c ＞0的解集为{x |﹣3＜x ＜2}，则函数y ＝ax 2+x ﹣a 的零点为（ ） A ．（3，0）和（﹣2，0） B ．（﹣3，0）和（2，0）C ．2和﹣3D ．﹣2和3解：不等式ax 2﹣x ﹣c ＞0的解集为{x |﹣3＜x ＜2}， 所以﹣3和2是方程ax 2﹣x ﹣c ＝0的解，由根与系数的关系知，{−3+2=1a −3×2=−c a ，解得a ＝﹣1，c ＝﹣6；所以函数y ＝ax 2+x ﹣c 可化为y ＝﹣x 2+x +6， 令y ＝0，得x 2﹣x ﹣6＝0，解得x ＝3或x ＝﹣2， 所以函数y ＝ax 2+x ﹣a 的零点为﹣2和3． 故选：D ．7．已知f （x ）={x 2−2tx +t 2，x ≤0x +1x +t ，x ＞0，若f （0）是f （x ）的最小值，则t 的取值范围为（ ） A ．[﹣1，2]B ．[﹣1，0]C ．[1，2]D ．[0，2]解：法一：排除法．当t＝0时，结论成立，排除C；当t＝﹣1时，f（0）不是最小值，排除A、B，选D．法二：直接法．由于当x＞0时，f（x）＝x+1x+t在x＝1时取得最小值为2+t，由题意当x≤0时，f（x）＝（x﹣t）2，若t≥0，此时最小值为f（0）＝t2，故t2≤t+2，即t2﹣t﹣2≤0，解得﹣1≤t≤2，此时0≤t≤2，若t＜0，则f（t）＜f（0），条件不成立，故选：D．8．实数a，b，c满足a2＝2a+c﹣b﹣1且a+b2+1＝0，则下列关系成立的是（）A．b＞a≥c B．c＞a＞b C．b＞c≥a D．c＞b＞a解：∵a+b2+1＝0，∴a≠1，∵实数a，b，c满足a2＝2a+c﹣b﹣1，∴（a﹣1）2＝c﹣b＞0，∴c＞b，∵a+b2+1＝0，∴a＝﹣b2﹣1，∴b﹣a＝b+b2+1=(b+12)2+34＞0，∴b＞a，∴c＞b＞a．故选：D．二、多项选择题9．下列命题为真命题的为（）A．∀x∈R，x2+x+1＞0B．当ac＞0时，∃x∈R，ax2+bx﹣c＝0C．|x﹣y|＝|x|+|y|成立的充要条件是xy≥0D．设a，b∈R，则“a≠0”是“ab≠0”的必要不充分条件解：对于A：∀x∈R，x2+x+1=(x+12)2+34＞0，故A正确；对于B：当ac＞0时，ax2+bx﹣c＝0，由于Δ＝b2﹣4ac大于0也可以等于0，故∃x∈R，ax2+bx﹣c＝0有解，故B正确；对于C ：|x ﹣y |＝|x |+|y |成立的充要条件是xy ≤0，故C 错误；对于D ：设a ，b ∈R ，当a ≠0时，当b ＝0时，ab ＝0，反之成立，故“a ≠0”是“ab ≠0”的必要不充分条件，故D 正确． 故选：ABD ．10．已知x ，y 是正数，且2x +y ＝1，下列叙述正确的是（ ） A ．2xy 最大值为14B ．4x 2+y 2的最小值为12C ．x （x +y ）最大值为14D ．1x+1y最小值为3+2√2解：因为x ，y 是正数，且2x +y ＝1，所以2xy ≤(2x+y 2)2=14，当且仅当2x ＝y =12时取等号，A 正确；4x 2+y 2＝（2x +y ）2﹣4xy ＝1﹣4xy ≥1−12=12，当且仅当2x ＝y =12时取等号，此时4x 2+y 2取得最小值12，B 正确； x （x +y ）≤(x+x+y 2)2=14，当且仅当x ＝x +y ，即y ＝0时取等号，根据题意显然y ＝0不成立，即等号不能取得，x （x +y ）没有最大值，C 错误；1x+1y=2x+y x+2x+y y =3+y x +2xy ≥3+2√2，当且仅当y x =2xy且2x +y ＝1，即x ＝1−√22，y =√2−1时取等号，此时1x+1y取得最小值3+2√2，D 正确．故选：ABD ．11．下列说法正确的是（ ）A ．函数f （x ）的值域是[﹣2，2]，则函数f （x +1）的值域为[﹣3，1]B ．既是奇函数又是偶函数的函数只有一个C ．若A ∪B ＝B ，则A ∩B ＝AD ．函数f （x ）的定义域是[﹣2，2]，则函数f （x +1）的定义域为[﹣3，1]解：对于A ，函数f （x ）的值域是[﹣2，2]，则函数f （x +1）的值域为[﹣2，2]，故A 错误；对于B ，既是奇函数又是偶函数的函数不只有一个，如x ∈（﹣1，1）时，f （x ）＝0满足f （﹣x ）＝f （x ），也满足f （﹣x ）＝﹣f （x ），即f （x ）既是奇函数又是偶函数；又f （x ）=√1−x 2+√x 2−1的定义域为{﹣1，1}，值域为{0}，满足f （﹣x ）＝f （x ），也满足f （﹣x ）＝﹣f （x ），即f （x ）既是奇函数又是偶函数，故B 错误； 对于C ，若A ∪B ＝B ，则A ⊆B ，因此A ∩B ＝A ，故C 正确对于D ，函数f （x ）的定义域是[﹣2，2]，即﹣2≤x ≤2，由﹣2≤x +1≤2，得﹣3≤x ≤1，即函数f （x +1）的定义域为[﹣3，1]，故D 正确． 故选：CD ．12．数学上，高斯符号（Gauss mark ）是指对取整符号和取小符号的统称，用于数论等领域．定义在数学特别是数论领域中，有时需要略去一个实数的小数部分只研究它的整数部分，或需要略去整数部分研究小数部分，因而引入高斯符号．设x ∈R ，用[x ]表示不超过x 的最大整数．比如： [1]＝1，[0]＝0，[﹣1]＝﹣1，[﹣1.2]＝﹣2，[1.3]＝1…，已知函数f(x)=[x]x(x ＞0)，则下列说法不正确的是（ ）A ．f （x ）的值域为[0，1）B ．f （x ）在（1，+∞）为减函数C ．方程f(x)=12无实根D ．方程f(x)=712仅有一个实根 解：由高斯函数的定义可得：当0＜x ＜1时，[x ]＝0，则f （x ）=[x]x =0， 当1≤x ＜2时，[x ]＝1，则f （x ）=[x]x =1x ； 当2≤x ＜3时，[x ]＝2，则f （x ）=[x]x =2x ； 当3≤x ＜4时，[x ]＝3，则f （x ）=[x]x =3x ； 当4≤x ＜5时，[x ]＝4，则f （x ）=[x]x =4x ， 绘制函数图象如图所示：对于A ，由图可知，f （x ）在（0，+∞）上的值域为（12，1]∪{0}，不正确；对于B ，当x ≥1时，f （x ）的每段函数都是单调递减，但是f （x ）在（1，+∞）不是减函数，不正确； 对于C ，由选项A 知，f （x ）在（0，+∞）上的值域为（12，1]∪{0}，所以方程f(x)=12无实根，正确； 对于D ，当1≤x ＜2时，f(x)=712，即1x =712，解得x =127∈[1，2），当2≤x ＜3时，f(x)=712，即2x=712，解得x =247∉[2，3），结合函数f （x ）图象知，方程f(x)=712仅有一个实根127，故正确． 故选：AB ． 三、填空题13．函数f(x)=√−x 2+2x +3的定义域为 [﹣1，3] ． 解：f(x)=√−x 2+2x +3， 令﹣x 2+2x +3≥0，解得﹣1≤x ≤3， 故函数f （x ）的定义域为[﹣1，3]． 故答案为：[﹣1，3]．14．已知函数f （x ）＝mx 2+nx +2（m ，n ∈R ）是定义在[2m ，m +3]上的偶函数，则函数g （x ）＝f （x ）+2x 在[﹣2，2]上的最小值为 ﹣6 ．解：因为函数f （x ）＝mx 2+nx +2（m ，n ∈R ）是定义在[2m ，m +3]上的偶函数， 故，即，则{2nx =0m =−1解得{n =0m =−1，所以g （x ）＝f （x ）+2x ＝﹣x 2+2x +2＝3﹣（x ﹣1）2，x ∈[﹣2，2]，所以g （﹣2）＝﹣（﹣2）2+2×（﹣2）+2＝﹣6，g （2）＝﹣22+2×2+2＝2， 则g （x ）min ＝﹣6， 故答案为：﹣6．15．股票是股份公司发给股东证明其所入股份的一种有价证券，它可以作为买卖对象和抵押品，是资金市场主要的长期信用工具之一．股票在公开市场交易时可涨可跌，在我国上海证券交易所交易的主板股票每个交易日上涨和下跌都不超过10%，当日上涨10%称为涨停，当日下跌10%称为跌停．某日贵州茅台每股的价格是1500元，若贵州茅台在1500元的价格上先涨停2天再跌停2天，则4天后每股的价格是 1470.15 元．解：由题意可知，四天后的价格为1500×（1+10%）2×（1﹣10%）2＝1470.15元． 故答案为：1470.15．16．设y ＝f （x ）是定义在R 上的函数，对任意的x ∈R ，恒有f （x ）+f （﹣x ）＝x 2成立，g(x)=f(x)−x 22，若y ＝f （x ）在（﹣∞，0]上单调递增，且f （2﹣a ）﹣f （a ）≥2﹣2a ，则实数a 的取值范围是 （﹣∞，1] ．解：由f （x ）+f （﹣x ）＝x 2，g(x)=f(x)−x 22， 可得g （x ）+g （﹣x ）＝f （x ）−x 22+f （﹣x ）−x 22=x 2﹣x 2＝0，所以g（x）为奇函数，由于y＝f（x）在（﹣∞，0]上单调递增，y=−x22在（﹣∞，0]上单调递增，所以g（x）在（﹣∞，0]上单调递增，从而g（x）在R上单调递增，由于f（2﹣a）﹣f（a）≥2﹣2a，则f（2﹣a）−(2−a)22≥f（a）−a22，即g（2﹣a）≥g（a），所以2﹣a≥a，故a≤1．故答案为：（﹣∞，1]．四、解答题17．（1）计算：(235)0+2−2×(214)−12−(0.01)0.5；（2）若实数a满足a 12+a−12=3，求a+a﹣1的值．解：（1）：(235)0+2−2×(214)−12−(0.01)0.5=1+14×(94)−12−0.1=1+14×23−110=1615；（2）a 12+a−12=3，两边同时平方可得，a+a﹣1+2＝9，故a+a﹣1＝7．18．已知函数f(x)=x+4x．（1）证明：f（x）在[2，+∞）为增函数；（2）求f（x）在[1，4]上的值域．（1）证明：在[2，+∞）上任取x1，x2，且x1＜x2，f(x1)−f(x2)=x1+4x1−(x2+4x2)=(x1−x2)⋅x1x2−4x1x2，∵x1＜x2，∴x1﹣x2＜0，x1∈[2，+∞），x2∈[2，+∞），∴x1x2﹣4＞0，∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），故f（x）在[2，+∞）上是增函数；（2）解：由（1）知：f（x）在[1，2]上是减函数，在（2，4）上是增函数，当x＝2时，有最小值4；当x＝1时，f（1）＝5，当x＝4时，f（4）＝5，∴函数的最大值为5，∴函数的值域为[4，5]．19．在①A∪B＝B；②“x∈A”是“x∈B”的充分不必要条件；③A∩B＝∅这三个条件中任选一个，补充到本题第（2）问的横线处，求解下列问题．问题：已知集合A ＝{x |a ﹣1≤x ≤2a +1}，B ＝{x |﹣1≤x ≤3}．（1）当a ＝2时，求A ∪B ；A ∩（∁R B ）；（2）若______，求实数a 的取值范围．解：（1）当a ＝2时，集合A ＝{x |1≤x ≤5}，B ＝{x |﹣1≤x ≤3}，∴∁R B ＝{x |x ＞3或x ＜﹣1}，所以A ∪B ＝{x |﹣1≤x ≤5}；A ∩（∁R B ）＝{x |3＜x ≤5}．（2）若选择①，A ∪B ＝B ，则A ⊆B ，当A ＝∅时，a ﹣1＞2a +1解得a ＜﹣2，当A ≠∅，又A ⊆B ，B ＝{x |﹣1≤x ≤3}，所以{a −1≤2a +1a −1≥−12a +1≤3，解得0≤a ≤1，所以实数a 的取值范围是（﹣∞，﹣2）∪[0，1]．若选择②，x ∈A 是x ∈B 的充分不必要条件，则A ⫋B ，当A ＝∅时，a ﹣1＞2a +1解得a ＜﹣2，当A ≠∅，又A ⫋B ，B ＝{x |﹣1≤x ≤3}，则{a −1≤2a +1a −1≥−12a +1＜3或{a −1≤2a +1a −1＞−12a +1≤3，解得0≤a ≤1，所以实数a 的取值范围是（﹣∞，﹣2）∪[0，1]．若选择③，A ∩B ＝∅，当A ＝∅时，a ﹣1＞2a +1解得a ＜﹣2，当A ≠∅，又A ∩B ＝∅，则{a −1≤2a +1a −1＞3或2a +1＜−1，解得a ＞4，或﹣2≤a ＜﹣1， 所以实数a 的取值范围是（﹣∞，﹣1）∪（4，+∞）．20．设函数f （x ）＝a •2x ﹣2﹣x （a ∈R ）． （1）若函数y ＝f （x ）为奇函数，求方程f(x)+32=0的实根；（2）若函数h （x ）＝f （x ）+4x +2﹣x 在x ∈[0，1]的最大值为﹣2，求实数a 的值．解：（1）∵f （x ）为奇函数，∴f （﹣x ）+f （x ）＝0，∴a •2﹣x ﹣2x +a •2x ﹣2﹣x ＝0， ∴（a ﹣1）•（2﹣x +2x ）＝0，得a ＝1．由f(x)+32=0，得2x ﹣2﹣x +32=0， ∴（2x +2）•（2•2x ﹣1）＝0，又2x ＞0， ∴2•2x ﹣1＝0，即x ＝﹣1，∴方程f(x)+32=0的实根为x ＝﹣1．（2）由h （x ）＝f （x ）+4x +2﹣x ，得h （x ）＝a •2x ﹣2﹣x +4x +2﹣x ，x ∈[0，1]， 令2x ＝t ∈[1，2]，函数h （x ）化为y ＝t 2+at ，t ∈[1，2]，对称轴t =−a 2，当−a 2≤32，即a ≥﹣3时，y max ＝4+2a ＝﹣2，得a ＝﹣3；当−a 2＞32，即a ＜﹣3时，y max ＝1+a ＝﹣2，得a ＝﹣3（舍）．综上：实数a 的值为﹣3．21．美国对中国芯片的技术封锁激发了中国“芯”的研究热潮．某公司研发的A ，B 两种芯片都已经获得成功．该公司研发芯片已经耗费资金2千万元，现在准备投入资金进行生产．经市场调查与预测，生产A 芯片的毛收入与投入的资金成正比，已知每投入1千万元，公司获得毛收入0.25千万元；生产B 芯片的毛收入y （千万元）与投入的资金x （千万元）的函数关系为y ＝kx a （x ＞0），其图像如图所示．（1）试分别求出生产A ，B 两种芯片的毛收入y （千万元）与投入资金x （千万元）的函数关系式；（2）现在公司准备投入40千万元资金同时生产A ，B 两种芯片，求可以获得的最大利润是多少．解：（1）∵生产A 芯片的毛收入与投入的资金成正比，∴可设y ＝mx （m ＞0），∵当x ＝1时，y ＝0.25，∴m ＝0.25，即y ＝0.25x ，∴生产A 芯片的毛收入y （千万元）与投入资金x （千万元）的函数关系式为y ＝0.25x ，∵生产B 芯片的函数y ＝kx a （x ＞0）图象过点（1，1），（4，2），∴{k =1k ⋅4a =2，解得{k =1a =12，∴y =x 12，即生产B 芯片的毛收入y （千万元）与投入资金x （千万元）的函数关系式为y =√x （x ＞0）． 综上所述，生产A 芯片的毛收入y （千万元）与投入资金x （千万元）的函数关系式为y ＝0.25x ， 生产B 芯片的毛收入y （千万元）与投入资金x （千万元）的函数关系式为y =√x （x ＞0）．（2）设投入x 千万元生产B 芯片，则投入（40﹣x ）千万元生产A 芯片，则公司所获利润f （x ）=0.25(40−x)+√x −2=−14(√x −2)2+9，故当√x =2，即x ＝4千万元时，公司所获利润最大，最大利润为9千万元．22．若函数y ＝f （x ）自变量的取值区间为[a ，b ]时，函数值的取值区间恰为[2b ，2a ]，就称区间[a ，b ]为y ＝f （x ）的一个“和谐区间”．已知函数g （x ）是定义在R 上的奇函数，当x ∈（0，+∞）时，g （x ）＝﹣x +3．（1）求g （x ）的解析式；（2）求函数g （x ）在（0，+∞）内的“和谐区间”；（3）若以函数g （x ）在定义域内所有“和谐区间”上的图象作为函数y ＝h （x ）的图象，是否存在实数m ，使集合{（x ，y ）|y ＝h （x ）}∩{（x ，y ）|y ＝x 2+m }恰含有2个元素．若存在，求出实数m 的取值集合；若不存在，说明理由．解：（1）因为g （x ）为R 上的奇函数，∴g （0）＝0，又当x ∈（0，+∞）时，g （x ）＝﹣x +3，所以，当x ∈（﹣∞，0）时，g （x ）＝﹣g （﹣x ）＝﹣（x +3）＝﹣x ﹣3，∴g(x)={−x −3，x ＜00，x =0−x +3，x ＞0；（2）设0＜a ＜b ，∵g （x ）在（0，+∞）上递单调递减，∴{2b =g(b)=−b +32a =g(a)=−a +3，即a ，b 是方程2x =−x +3的两个不等正根． ∵0＜a ＜b ，∴{a =1b =2， ∴g （x ）在（0，+∞）内的“和谐区间”为[1，2]；（3）设[a ，b ]为g （x ）的一个“和谐区间”，则{a ＜b 2b ＜2a，∴a ，b 同号．当a ＜b ＜0时，同理可求g （x ）在（﹣∞，0）内的“和谐区间”为[﹣2，﹣1]．∴ℎ(x)={−x +3，x ∈[1，2]−x −3，x ∈[−2，−1]， 依题意，抛物线y ＝x 2+m 与函数h （x ）的图象有两个交点时，一个交点在第一象限，一个交点在第三象限．因此m 应当使方程x 2+m ＝﹣x +3在[1，2]内恰有一个实数根，并且使方程x 2+m ＝﹣x ﹣3，在[﹣2，﹣1]内恰有一个实数．由方程x 2+m ＝﹣x +3，即x 2+x +m ﹣3＝0在[1，2]内恰有一根，令F （x ）＝x 2+x +m ﹣3，则{F(1)=m −1≤0F(2)=m +3≥0，解得﹣3≤m ≤1； 由方程x 2+m ＝﹣x ﹣3，即x 2+x +m +3＝0在[﹣2，﹣1]内恰有一根，令G （x ）＝x 2+x +m +3，则{G(−1)=m +3≤0G(−2)=m +5≥0，解得﹣5≤m ≤﹣3． 综上可知，实数m 的取值集合为{﹣3}．。

浙江省重点高中排名一览表一、宁波市镇海中学创建于1911年，坐落于浙江宁波镇海，其前身蛟川书院创办于1743年(清乾隆八年)；1978年、1984年相继被确定为浙江省十四所重点中学和浙江省首批办好的十八所重点中学之一；1995年被评为首批“浙江省一级重点中学”，2014年被授予首批“浙江省一级普通高中特色示范学校”称号。

宁波市镇海中学创建于清宣统三年（1911年），原名“镇海中学堂”； 1912年，改名“镇海中学校”；1915年，改制为“乙种商业职业学校”；1926年，改名为“镇海县立初级中学”；1952年，更名为“镇海县第一初级中学”；1956年，与私立辛成中学合并成立“浙江省镇海中学”，1959年3月，更名为“浙江省宁波镇海中学”；1985年，改名为“宁波市镇海中学”。

二、杭州市第二中学由杭州市教育局主管的公立全日制普通高级中学，1978年被定为浙江省重点中学，1980年被列为浙江省首批办好的18所重点中学之一，1995年9月被认定为浙江省一级重点中学，2014年被评为首批浙江省一级普通高中特色示范学校。

[1]浙江省杭州第二中学的前身为创办于1899年的私立蕙兰中学和创办于1939年的国立浙江大学附属中学；1951年8月，两校在“蕙兰”原址合并，改称浙江省杭州第二中学；1969年5月，学校改名为“杭州玻璃厂五·七学校”；1971年12月，学校复名“浙江省杭州第二中学”。

三、杭州外国语学校杭州外国语学校创建于1964年，1982年开设在职中学教师英语专业大专班等各类外语培训班；1985年，与浙江师范大学联合创办英语大专班；2013年，杭州外国语学校由“国有民办”体制转为公办体制。

四、杭州学军中学始建于1956年，初名杭州市第十四初级中学，后更名为浙江师范大学附属中学、杭州大学附属中学。

1970年更名。

1978年被浙江省政府授予浙江省首批重点中学。

五、浙江省慈溪中学创办于1956年，曾易名慈溪县浒山中学、浒山镇“五七”中学、慈溪县建筑工程公司“五七”中学等，1979年恢复“浙江省慈溪中学”校名。

一、绍兴一中据不完全统计，我校第一批上线人数达605人（包括免试提前保送进清华大学5人、复旦大学1人、中国科技大学2人及体艺和国外名校等）。

理科700分以上11人，理科最高分737分，文科最高分698分。

二、镇海中学据统计，该校理科考生中，700分以上共有68个，其中720分以上的有22个，725分以上的18个，最高分757分（省理科状元）；文科考生中，700分以上的共２个，690分以上的共10个，最高分707分。

尽管还未统计“一本”上线率，但该校校长估计，今年的“一本”上线率与去年差不多，超过90％。

三、东阳中学东阳中学今年高考成绩继续创历史新高。

文、理科重点上线人数达605人（不含艺术、体育），其中理科上重点线人数542人，高分超过700分的共有25人，上重点线人数、上重点线比例、高分段人数继续位居金华市第一。

卢南峰同学以714分获浙江省文科总分第四名、金华市文科总分第一名，徐战同学被免试保送北京大学。

四、金华一中2012年我校高考成绩喜人：已确定保送、自主招生上清华、北大8人，高考成绩总分700分以上36人，文理科一本总上一率达74.2%，文科一本上线率达74.4%，上重点线人数达604人。

五、富阳中学2012高考成绩揭晓，富阳中学又迎来一个丰收年。

上一本线人数再创新高，文理科上一本线总人数为656（文科：181；理科474，保送清华大学1人）。

文科680以上10人，理科720以上6人，外加保送清华大学1人。

六、台州中学今年台州中学高考上重点人数673人，再创历史新高，重点人数、重点率、尖子生人数均为台州市第一。

文科630分以上83人，理科640分以上197人，其中陈碧萱同学以749分居浙江省理科第2名，为台州市理科状元，许志超同学714分为台州市文科状元。

七、衢州二中上第一批（重点）线669人（不含保送生，体艺生），另有9人已被北大（3人）、清华（1人）、人大（1人）、浙大（1人）、中科大（1人）、新加坡名校（2人）提前录取。

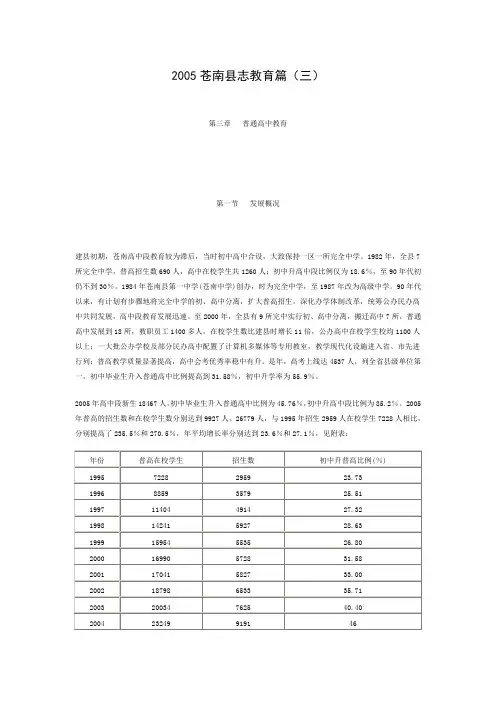
2005苍南县志教育篇（三）第三章普通高中教育第一节发展概况建县初期，苍南高中段教育较为滞后，当时初中高中合设，大致保持一区一所完全中学。

1982年，全县7所完全中学，普高招生数690人，高中在校学生共1260人；初中升高中段比例仅为18.6％，至90年代初仍不到30％。

1984年苍南县第一中学(苍南中学)创办，时为完全中学，至1987年改为高级中学。

90年代以来，有计划有步骤地将完全中学的初、高中分离，扩大普高招生，深化办学体制改革，统筹公办民办高中共同发展，高中段教育发展迅速。

至2000年，全县有9所完中实行初、高中分离，搬迁高中7所，普通高中发展到18所，教职员工1400多人，在校学生数比建县时增长11倍，公办高中在校学生校均1100人以上；一大批公办学校及部分民办高中配置了计算机多媒体等专用教室，教学现代化设施进入省、市先进行列；普高教学质量显著提高，高中会考优秀率稳中有升。

是年，高考上线达4537人，列全省县级单位第一。

初中毕业生升入普通高中比例提高到31.58％，初中升学率为55.9％。

2005年高中段新生18467人，初中毕业生升入普通高中比例为45.76％，初中升高中段比例为85.2％。

2005年普高的招生数和在校学生数分别达到9927人、26779人，与1995年招生2959人在校学生7228人相比，分别提高了235.5％和270.5％，年平均增长率分别达到23.6％和27.1％，见附表：1997年苍南县实现“两基”以后，作为基础教育范畴内较高层次的普通高中教育，加快改革步伐，各校按照省市等级评估标准办学，实行目标管理。

1998年苍南一中被评为省一级重点中学。

2003年有4所普高接受省重点学校评估。

2005年全县普高19所（见附表）其中共有8所普高命名为省重点中学。

第二节学制与课程1981年，我县中学学制为三二分段的五年制，高中2年，据《全日制五年制中学教学计划试行草案的修订意见》，课程设政治、语文、数学、外语、物理、化学、历史、地理、生物、体育、劳动技术等。

浙江省一级、二级、三级重点高中一、省一级重点中学杭州市：杭州高级中学杭州第二中学浙江大学附属中学杭州学军中学杭州第四中学杭州第十四中学杭师院附属三墩高级中学杭州长河高级中学杭州外国语学校萧山中学萧山区第二高级中学萧山区第三高级中学萧山区第五高级中学余杭高级中学余杭第二高级中学富阳中学富阳市第二高级中学富阳市新登中学桐庐中学临安中学临安昌化中学临安市於潜中学淳安中学严州中学宁波市：镇海中学宁波效实中学宁波中学鄞州中学慈溪中学余姚中学宁海中学象山中学奉化市第一中学北仑中学鄞州区姜山中学鄞州区鄞江中学慈溪市浒山中学宁波第二中学宁波万里国际学校中学(民办) 宁波华茂外国语学校(民办) 鄞州区正始中学宁波市李惠利中学镇海区龙赛中学宁海县知恩中学慈溪市杨贤江中学温州市：温州中学温州第二高级中学瓯海中学瑞安中学乐清中学平阳县第一中学苍南县第一中学永嘉中学嘉兴市:嘉兴市第一中学嘉兴市高级中学平湖中学海宁市高级中学桐乡市高级中学海盐元济高级中学嘉善高级中学嘉兴市秀州中学桐乡市第一中学平湖市当湖高级中学桐乡市茅盾中学海盐高级中学嘉善第二高级中学湖州市：湖州中学湖州市第二中学湖州市菱湖中学德清县第一中学德清县高级中学安吉高级中学长兴中学德清县第三中学长兴县华盛虹溪中学（民办）绍兴市：绍兴市第一中学上虞春晖中学诸暨中学绍兴县柯桥中学嵊州市第一中学绍兴市稽山中学上虞中学新昌中学绍兴县鲁迅中学诸暨市牌头中学绍兴县越崎中学金华市：金华市第一中学浙江师范大学附属中学（金华二中）金华市汤溪高级中学兰溪市第一中学东阳中学义乌中学永康市第一中学武义第一中学浦江中学磐安中学金华艾青中学义乌市第二中学衢州市：衢州第二中学衢州第一中学江山中学龙游中学丽水市：丽水中学缙云中学遂昌中学青田中学云和中学龙泉市第一中学庆元中学松阳县第一中学景宁中学台州市：台州中学温岭中学天台中学椒江区第一中学黄岩中学仙居中学路桥中学三门中学温岭市新河中学临海市回浦中学温岭市第二中学临海市大田中学台州市书生中学（民办）玉环县楚门中学天台县平桥中学舟山市：舟山中学岱山中学普陀中学定海一中二、省二级重点中学杭州市：杭州市源清中学杭州西湖高级中学杭州市第二中学分校杭州市第四中学分校杭州第七中学杭州第九中学杭州第十一中学萧山区第八高级中学建德市新安江中学宁波市：余姚市第八中学宁波市第三中学宁波市慈湖中学慈溪市逍林中学慈溪市观城中学奉化市武岭中学宁波市第四中学象山县第二中学慈溪市周巷中学北仑区柴桥中学余姚市第七中学鄞州区同济中学象山县第三中学余姚市第五中学慈溪市育才中学（民办）慈溪市实验高中（民办）余姚市高风中学（民办) 象山县滨海学校（民办）温州市：洞头县第一中学苍南县龙港高级中学瓯海区任岩松高级中学瑞安市第四中学乐清市柳市中学泰顺县第一中学乐清市虹桥中学乐清第二中学永嘉县罗浮中学温州市第十五中学苍南县钱库高级中学嘉兴市：嘉兴市第四高级中学嘉善中学海宁宏达高级中学（民办）嘉兴三中海宁市第一中学嘉兴第五高级中学湖州市：湖州市双林中学安吉县昌硕高级中学湖州市第一中学湖州市吴兴高级中学湖州市南浔中学绍兴市：嵊州市黄泽中学嵊州市第二中学嵊州市崇仁中学新昌县澄潭中学诸暨市天马学校（民办）私立诸暨高级中学（民办）诸暨荣怀学校（民办）诸暨市草塔中学诸暨市学勉中学诸暨市第二高级中学绍兴市高级中学金华市：东阳市第二高级中学金华市第八中学义乌市大成中学东阳巍山高级中学东阳市中天高级中学（民办）兰溪市第三中学金华市第六中学义乌市第三中学武义第三中学永康明珠学校（民办）浦江县第三中学永康市第二中学衢州市：巨化集团公司职工子女中学常山县第一中学开化中学江山市滨江高级中学江山市实验中学（民办）丽水市：丽水学院附属高级中学缙云县新建中学台州市：椒江区三梅中学玉环县玉城中学温岭市之江高级中学（民办）温岭市大溪中学温岭市箬横中学温岭市松门中学临海市杜桥中学台州市路桥区蓬街私立中学（民办）天台县育青中学（民办）黄岩区第二高级中学舟山市：嵊泗中学舟山二中三、省三级重点中学杭州市：杭州余杭中学杭州市塘栖中学建德市寿昌中学萧山区第六高级中学杭州市绿城育华学校（民办）余杭区瓶窑中学淳安县威坪中学桐庐分水高级中学（原桐二高）临安市天目外国语学校（民办）杭州市长征中学杭州市第十中学富阳市大源中学富阳市场口中学萧山区第十高级中学杭州市夏衍中学萧山区第十一高级中学桐庐富春高级中学（桐三高、四高合并）淳安县汾口中学宁波市：鄞州区咸祥中学余姚市第三中学宁波市四明中学鄞州区五乡中学北仑区明港中学奉化市宁波东方外国语学校（民办）慈溪市三山中学慈溪市龙山中学余姚市第二中学温州市：文成中学瑞安市第五中学瑞安市第三中学苍南县宜山高级中学苍南县金乡高级中学瑞安市第十中学苍南县灵溪第一高级中学苍南县灵溪第二高级中学苍南县振清外国语学校（民办) 平阳县第二中学瑞安市隆山高级中学瓯海区第二高级中学瓯海区梧田高级中学乐清第三中学乐清白象中学温州市第八中学温州市第二十二中学瓯海区三溪中学温州市育英国际实验学校（民办）嘉兴市：桐乡市第二中学南湖中学平湖市乍浦中学平湖市新华爱心高级中学（民办）海宁中学湖州市：安吉孝丰高级中学长兴金陵高级中学湖州市第五中学绍兴市：诸暨市湄池中学上虞市东关中学上虞市城南中学上虞市崧厦中学绍兴县鉴湖中学浙江华维外国语学校（民办）金华市：东阳市南马高级中学东阳市顺风高级中学（民办）浦江县第二中学武义县第二中学东阳市横店高级中学（民办）兰溪兰荫中学（民办）义乌市第四中学东阳市六石高级中学兰溪市第五中学义乌市私立群星学校（民办）永康市古丽中学（民办）衢州市：衢州三中丽水市：缙云县壶镇中学台州市：临海市第六中学温岭市泽国中学台州市实验中学（民办）舟山市：普陀第三中学普陀区六横中学定海区白泉高级中学岱山县大衢中学。

光荣榜——苍南中学2010年重点大学上线名单一、文科（22名）刘惠璇陈婷婷戴小洁方穗黄小若郑欣欣李则查陈欣怡陈程周丹丹李永王珊珊魏巍李明明宋星星吴世伟林维钢陈兵兵周林子王琨张仁将王蓓蓓二、理科（291名）陈强黄系刘伟伟方文曲林敏李丕松林奕黄继谦徐成文陈勇侯良哨王伟伟刘星星黄陈静杨思思肖苗苗郑璐高洁陈婷婷薛志村黄宗强陈晓霞余翔翔洪珊珊黄昭帅蒋瑶瑶肖云姿蔡叶荷徐蒙蒙张梦婷陈静郑源雷王和阳赖联贺林佳佳易永坤黄崇德徐启葳罗琨林高侠苏义焜黄珊珊安孝宇周涵依吴鹏王丽娟吴盈盈黄绍远陈新新赖必必张敬李昭昭章婷婷郑光鹏章乒乒温学敏韩红伟蔡希希章坤吕莉莉陈德毅曹允宁张钟楼朱薇薇罗莉黄颖颖陈盛存曾瑞悦陈文彦杨圣别张礼权倪田乐余秋华林笑笑陈玲萍吴青鸿章显伟洪德取许屿冰李笑笑陈兴缪文杰宋海东丁霄霄陈硕邓婷婷陈发毅陈璇姜晓节谢永恒彭美华吴梦娜李坤赵小慧罗大思吴法铨洪东炬苏婷婷姜立立郑国周黄星星温端强林翠平许莹莹方晓辉吴洁陈新新李薪芳颜洁心马乾群方飞雄赖芳芳黄咪咪李文婷林秋雁吴舜乐陈彬彬林佳佳林萍萍林翔林彩文梁世润邓洋林益铭陈先宏程源知黄小良杨秋夏陈中思黄小燕许振东陈成樟陈璐童昌希陈新新郑书瑶陈冲陈世雄林小玉梁峰郭雅坤陈宗安陈启炜张维望郑忠鹏黄靖杨菲菲陈星星林传陆陈乃横张新新侯世鹏李崇煜张怡巧朱洁子王靖吴侠朱书奔江思源陈小芝陈文俊缪苹苹周文珍温建钧许允纯谢佳形黄芬芬张世苗易星星夏莹杨蕾何升广陈玉宣陈朝逸薛承授王瑞栋周甲武黄晓涵蒋招杰陈伟伟林孝聪杨程程钟花晓欧璐璐黄玉环苏维维陈斌吕欣欣吴联快蔡盛赢李梦余东东吴文文黄淑楠朱晨枫方荣荣黄园园黄莹莹冯利陈其成吴保成欧昆翔陈津津蔡蓓蓓杨佳佳周颖陈杰李波钟雷雷黄焕郑珊珊梁晗陈倩云张晓俊罗娇娇沈满意杨玲玲叶培虞文杰许振赐陈少青陈晓静张辉林项彬彬郑文镇姜陈静叶子威黄寰朱苗苗李莹莹林初超蒋谢斌董玉青余佩佩郑秀秀王进潇陈祥杰陈芳王恩待王晶晶许明炬林孝炫吴文意林小菲蒋贤林沈益根林倩文曾瑞慧李芳芳罗白云郑哲黄纯纯许新望夏建华林萍萍吴大宇吴强强陈建立侯良策李国炜王文浩李国强章阳余建概周涵薇王拉拉谢树栋李绍武陈孝敬陈晓庆林迎午钱玲玲项杰黄静静李沛黄永墙陈云阔章婷婷管方舒林久宁黄思思杨联斌钟嫣然黄祖明缪磊韩丝丝陈孝炬陈冲李彬彬陈聪聪蒋扬扬三、艺术、体育类（6人）体育兼文科（1人）：陈杰艺术兼文科（4人）：蔡霜霜章珊珊李莉莉林怡艺术兼理科（1人）：陈荣伟。