作图法解题

作图法解题作者悦读越好解决应用题一般有四个步骤：第一步：弄清已知条件和问题；第二步:分析数量关系；第三步:列式计算；第四步:检验作答。

其中：前两步是关键。

怎么分析问题呢？有时候可以借助于画图来分析问题，比如例1。

例1.一个木器厂要生产一批桌子。

原计划每天生产48张，实际每天比原计划多生产2张，结果提前一天完成生产任务。

原计划要生产多少张桌子？在看本文分析之前，大家可以自己先动手做一下，然后我们给出我们的解题方法。

分析：要求原计划生产多少张，也就是原计划的生产总量，拿原计划每天的工作量乘原计划的天数就可以了，题目中只有每天的量没有天数，因此需要先求出计划天数。

或者，原计划的生产总量与实际的生产总量相同，因此用实际每天的生产量乘实际的天数也是可以的。

同样，题目只有实际每天的生产量，没有实际的天数，因此如果能够求出实际的天数也能解决问题。

本题在不用方程的情况下，可以用作图法解法解决。

图1 图2图1中长方形的长代表计划的天数，宽代表计划的每天的生产量，那么图1的面积就是计划生产总量。

图2中长方形的长代表实际的天数，宽代表实际的每天的生产量，那么图2的面积就是实际生产总量。

比较图1和图2，图2的长比图1的长“少一天”，图2的宽比图1的宽“多2个”。

我们知道，计划的生产总量和实际的生产总量是一样，因此将图1和图2做一个叠加。

得到图3，图3被分成3个区域①②③，如图4所示，我们应该能够分析出②和③的面积相等。

图3 图4详细分析一下②和③，如图5所示。

不难看出③的长就是计划每天的生产量48，③的宽是计划比实际多的1天，因此③的面积为48×1=48，同样②的面积也是48。

再来看一个②，②的宽等于实际比计划多生产的2个，②的长是什么含义呢？②的长就是实际的天数，因此可以求出实际天数为48÷2=24天。

至此，问题再无难度。

图5实际的生产总量：（48+2）×（1×48÷2）=1200(张)计划的生产总量：48×（1×48÷2+1）=1200（张）答：原计划要生产1200张桌子？这道题目当然还有其他的分析方法，本文主要是想介绍作图法解决问题，当我们借助于作图解决问题时，题目中的各个量的关系其实是比较直观清楚的，希望我们能够借助了作图的这个工具。

练习五（作图法解题）姓名1、两根同样长的铁丝，第一根剪去18厘米，第二根剪去26厘米。

余下的铁丝，第一根是第二根的3倍，原来每根铁丝各长（）厘米。

2、五（1）班50名同学中，参加语文兴趣小组的有20人，参加数学兴趣小组的有26人，既没有参加语文兴趣小组也没有参加数学兴趣小组的有12人。

那么参加数学兴趣小组且没有参加语文兴趣小组的有（）人，既参加语文兴趣小组又参加数学兴趣小组的有（）人。

3、虹桥瓜果批发部有甲、乙两个仓库，乙仓库的水果存量是甲仓库的5倍。

如果从甲仓库中抽出5吨水果放到乙仓库，那么乙仓库的水果数就是甲仓库的8倍。

甲仓库原来的水果存数是（）吨，乙仓库原来的水果存数是（）吨。

4、城南小学的少先队员帮助学校清理基建工地。

已知甲工地比乙工地大一倍，上午他们在甲工地清理了半天；下午将人数对半分，一半留在甲工地，另一半到乙工地清理。

到收工时，甲工地已清理完毕，乙工地还剩一小块需1人再清理1天才能完工。

如果每个人的工作效率相等，那么共有（）名少先队员参加了清理。

5、甲在南北路上，由南向北行进，乙在东西路上，由西向东行进。

甲出发的地点在两条路交叉点南面1120米，乙在交叉点出发，两人同时开始行进；4分钟后，甲、乙两人所在的位置与交叉点等远（这时甲仍在交叉点南）；再经过52分钟后，两人所在的位置又距交叉点等远（这时甲在交叉口北）。

甲每分钟行（）米，乙每分钟行（）米。

6、草地上有80只兔子，其中有55只小兔子，63只灰兔，10只大白兔。

小灰兔有（）只。

7、甲、乙两列车同时从A、B两地相对开出，第一次在离A地75千米处相遇，相遇后继续前进到达目的地后又立刻返回，第二次相遇在离B地55千米处。

A、B两地的距离是（）千米。

8、有一个长方形花圃，如果长增加6米，或者宽增加4米，面积都比原来增加48平方米，这个花圃原来的面积是（）平方米。

9、一个长方形周长是24厘米，如果长和宽各增加5厘米，面积增加（）平方厘米。

画图法解应用题苏联教育家苏霍姆林斯基曾经说过：“如果哪个学生学会了画应用题，我就可以有把握地说，他一定能学会解应用题。

”可见，画图对于小学数学解决问题的重要性。

在解答一些应用题时，用作图法可以把题目的数量关系揭示出来，以其形象、直观的特点，使题意一目了然，对解答条件隐蔽，复杂疑难应用题，能起到化难为易，化繁为简的作用，从而有助于快速找到解题的途径，有效地提高学生的自我学习能力和创新能力，使学生学会学习。

作图法解应用题中，常见的数学图有以下几种：一、线段图线段图是由几条线段组合在一起，用来表示应用题中的数量关系，帮助人们分析题意，解答问题的一种平面图形。

线段图在小学数学应用题学习中它可以帮助学生轻松地解答复杂关系的应用题，强化数量关系的表述训练，能根据数量关系有序地进行解题演练。

举例：欢欢和喵喵共有25个本子，如果欢欢用去了3个本子，喵喵买回2个本子，那么她们的本子就一样多了，你知道她们原来各有本子多少个吗？列式计算：喵喵 (25－3－2)÷2＝10(本) 欢欢 25－10＝15(本)二、树形图在解答应用题时，我们常常采用枚举法把所有符合题目条件的对象一一列举出来。

我们采用画树形图的方法，借助树的分叉特征构造出的树形图可以对数学问题中有可能出现的多种可能逐一例举出来，不仅形象直观，而且有条理又不易重复或遗漏，使人一目了然，有助于作出正确的判断。

举例：一个口袋中装有红、白、绿三只小球，另一只口袋中装有红、白两只小球。

现从两只口袋中各取一只小球，求两只小球颜色一样的概率是多少？从图中可以看出，两只小球颜色搭配的可能性共6种，而两只小球颜色一样的可能性只有(红-红)，(白-白)共2种，所以两只小球颜色一样的概率为三分之一。

三、集合图在数学中，经常用平面上封闭曲线的内部代表集合，以及用以表示集合之间的关系，这样的图形称之为“集合图”。

举例：参加跳绳的有6人，参加踢毽子的有7人，两项都参加的有3人，这个组共有几人？6＋7－3＝10（人）四、情景图把复杂的数学问题用简单的图画表示，把情景再现出来，让人有身临其境的感觉，便于学生理解和分析应用题。

第二周作图法解题专题简析:用作图的方法把应用题的数量关系提示出来，使题意形象具体, 一目了然，以便较快地找到解题的途径，它对解答条件隐蔽、复杂疑难的应用题，能起化难为易的作用。

在解答已知一个数或者几个数的和差、倍差及相互之间的关系, 求其中一个数或者几个数问题等应用题时，我们可以抓住题中给出的数量关系，借助线段图进行分析，从而列出算式。

例题1五（1）班的男生人数和女生人数同样多。

抽去18名男生和26名女生参加合唱队后，剩下的男生人数是女生的3倍。

五（1）班原有男、女生各多少人?分析根据题意作出示意图:18名从图中可以看出，由于女生比男生多抽去26—18=8名去合唱队, 所以，剩下的男生人数是女生人数的3倍，而这8名同学正好相当于剩下女生人数的2倍，剩下的女生人数有8-2=4名，原来女生人数是26 + 4=30 名。

练习一1,两根电线一样长，第一根剪去50厘米，第二根剪去180厘米后，剩下部分，第一根是第二根长度的3倍。

这两根电线原来共长多少厘米?2,甲、乙两筐水果个数一样多，从第一筐中取出31个，第二筐中取出19个后，第二筐剩下的个数是第一筐的4倍。

原来两筐水果各有多少个?3,哥哥现存的钱是弟弟的5倍，如果哥哥再存20元，弟弟再存100元，二人的存款正好相等。

哥哥原来存有多少钱?例题2同学们做纸花，做了36朵黄花，做的红花比黄花和紫花的总数还多12朵。

红花比紫花多几朵?分析通过线段图来观察:黄花36朵紫花红花从图中可以看出：红花比紫花多的朵数由两部分组成，一部分是36朵，另一部分是12朵，所以，红花比紫花多36+ 12=48朵。

练习二1，奶奶家养了25只鸭子，养的鸡比鸭和鹅的总数还多10 只。

奶奶家养的鸡比鹅多几只？2，批发部运来一批水果，其中梨65 筐，苹果比梨和香蕉的总数还多24 筐。

运来的香蕉比苹果少多少筐？3,两根电线共长59 米，如果第一根电线剪去 3 米后，第一根电线的长度就是第二根的 3 倍，求原来两根电线各长多少米？4,甲、乙两筐苹果共重83千克，如果从甲筐取出 3 千克后，甲筐苹果就是乙筐的 4 倍，甲、乙两筐苹果各重多少千克？5、学校图书馆共有科技书和故事书250 本，又买来50本科技书后，科技书的本数是故事书的 2 倍，学校图书馆原来各有科技书和故事书多少本？6、参加奥赛集训的男生和女生共有21名，如果女生减少5名, 男生人数就是女生的3倍，参加奥赛集训的男、女生各多少名?3,期末测试中，明明的语文得了90分。

作图题-解题技法作图题是一种需要利用图像表示的问题。

解题技法涉及到观察、推理和分析等过程。

在解题过程中，我们可以采用以下几种技巧：仔细观察图形，理解图形的性质，发现其中的规律，通过图形间的关系进行推理和分析，利用已知条件推导出未知答案等。

下面将以一个实际的作图题为例，详细介绍解题技法。

假设有一道作图题如下：在一个直角坐标系中，有四个点，分别为A(3,5)、B(7,5)、C(7,11)和D(3,11)。

请作出一个四边形ABCD，并回答以下问题：1.四边形ABCD的边长是多少？2.四边形ABCD的周长是多少？3.四边形ABCD的面积是多少？```C(7,11)A(3,5)------B(7,5)D(3,11)```1.四边形ABCD的边长可以通过计算每条边的长度来得到。

根据已知信息以及直角坐标系中计算两点之间距离的公式，我们可以计算出四边形ABCD的四条边的长度为：AB=√[(7-3)^2+(5-5)^2]=√[16]=4BC=√[(7-7)^2+(11-5)^2]=√[36]=6CD=√[(3-7)^2+(11-11)^2]=√[16]=4DA=√[(3-3)^2+(11-5)^2]=√[36]=6所以四边形ABCD的边长分别为4、6、4和62.四边形ABCD的周长可以通过将四条边的长度相加得到。

所以四边形ABCD的周长为4+6+4+6=20。

3.四边形ABCD的面积可以通过计算两条对角线分成的两个三角形的面积之和来得到。

根据已知信息以及直角坐标系中计算两点之间距离的公式，我们可以计算出对角线AC和对角线BD的长度为：AC=√[(7-3)^2+(11-5)^2]=√[36]=6BD=√[(3-7)^2+(11-5)^2]=√[36]=6所以四边形ABCD的面积可以通过计算两个三角形的面积之和来得到。

我们可以使用海伦公式（也称为Heron's Formula）来计算三角形的面积。

海伦公式如下：S=√[s(s-a)(s-b)(s-c)]其中，S为三角形的面积，a、b和c为三角形的三边的长度，s为半周长（s=(a+b+c)/2）。

解题方法用作图法解题解题方法-----用作图法解题姓名知识、规律、方法把应用题中的已知条件和问题用画图的形式表示出来，使问题的内容具体形象，便于我们理解题意，分析题目中的数量关系，从而找到解题的方法，这就是作图法。

作图，除了打架常用的线段图，有时，根据题目的需要，也可以用条形图、流程图等图形来表示。

作图时，一般情况下，首先要分清题中有哪几种数量，用几条线段来表示比较合适；然后抓住数量之间的倍数关系、多少关系等，正确地画出不同的长短的线段。

范例、拓展例1 甲、乙两筐苹果的个数相同。

从甲筐里拿出了54个苹果，从乙筐中拿出了78个苹果后，甲筐剩下的苹果数是乙筐苹果个数的3倍。

两筐原来各有多少个苹果？拓展一有三捆布，已知第一捆的米数是第二捆的一半，第二捆比第三捆少18米，第三捆的米数是第一捆的5倍。

三捆布总共多少米？拓展二四年级有三个班，如果把甲班的1名学生调到乙班，两班人数相等；如果把乙班1名学生调到丙班，丙班比乙班多2人。

调动前甲班和丙班哪个班人多？多几人？拓展三小明问李老师今年有多少岁，李老师说：“当我像你这么大时，你才3岁；当你像我这么大时，我已经42岁了。

”李老师今年多少岁？例2 四年级一班有42名同学，全部参加了学校的兴趣小组活动。

其中参加版画组的有32人，参加鼓号队的有21人。

两个队都参加的有多少人？拓展一三年级一班参加期末考试的41名同学中，有27人数学得了优秀，有20人语文得了优秀，两门都没得优秀的有5人。

那么，有多少人两门都得了优秀？拓展二某区100个外语教师懂英语或俄语，其中懂得英语的有75人，既懂英语又懂俄语的有20人，那么懂俄语的教师为多少人？拓展三六年级一班有学生46人，其中会骑自行车的有17人，会游泳的有14人，既会骑车又会游泳的有4人。

两样都不会的有多少人？拓展四在100名学生中，音乐爱好者有56人，体育爱好者有75人，那么既爱好音乐又爱好体育的最少有多少人，最多有多少人？练习：1、一个班有45人做语文、数学作业，下课时，每人至少都做完了一门作业。

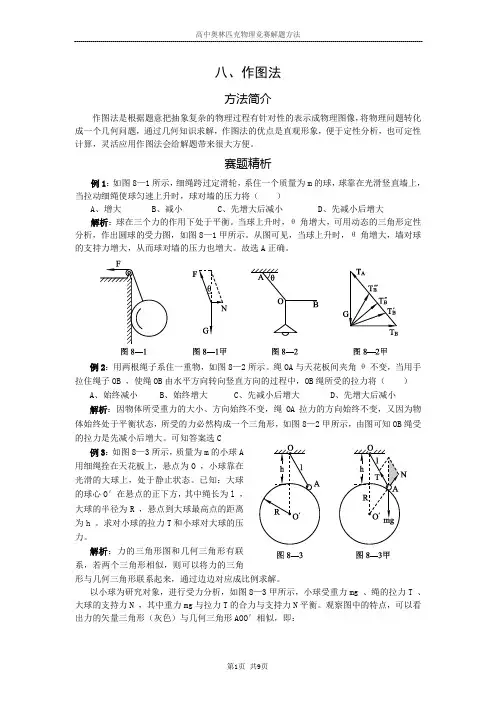
八、作图法方法简介作图法是根据题意把抽象复杂的物理过程有针对性的表示成物理图像，将物理问题转化成一个几何问题，通过几何知识求解，作图法的优点是直观形象，便于定性分析，也可定性计算，灵活应用作图法会给解题带来很大方便。

赛题精析例1：如图8—1所示，细绳跨过定滑轮，系住一个质量为m的球，球靠在光滑竖直墙上，当拉动细绳使球匀速上升时，球对墙的压力将（）A、增大B、减小C、先增大后减小D、先减小后增大解析：球在三个力的作用下处于平衡。

当球上升时，θ角增大，可用动态的三角形定性分析，作出圆球的受力图，如图8—1甲所示。

从图可见，当球上升时，θ角增大，墙对球的支持力增大，从而球对墙的压力也增大。

故选A正确。

例2：用两根绳子系住一重物，如图8—2所示。

绳OA与天花板间夹角θ不变，当用手拉住绳子OB ，使绳OB由水平方向转向竖直方向的过程中，OB绳所受的拉力将（）A、始终减小B、始终增大C、先减小后增大D、先增大后减小解析：因物体所受重力的大小、方向始终不变，绳OA拉力的方向始终不变，又因为物体始终处于平衡状态，所受的力必然构成一个三角形，如图8—2甲所示，由图可知OB绳受的拉力是先减小后增大。

可知答案选C例3：如图8—3所示，质量为m的小球A用细绳拴在天花板上，悬点为O ，小球靠在光滑的大球上，处于静止状态。

已知：大球的球心O′在悬点的正下方，其中绳长为l ，大球的半径为R ，悬点到大球最高点的距离为h 。

求对小球的拉力T和小球对大球的压力。

解析：力的三角形图和几何三角形有联系，若两个三角形相似，则可以将力的三角形与几何三角形联系起来，通过边边对应成比例求解。

以小球为研究对象，进行受力分析，如图8—3甲所示，小球受重力mg 、绳的拉力T 、大球的支持力N ，其中重力mg与拉力T的合力与支持力N平衡。

观察图中的特点，可以看出力的矢量三角形（灰色）与几何三角形AOO′相似，即：T l =mg h R +，N R =mg h R+ 所以绳的拉力：T =l h R+mg 小球对大球的压力：N ′= N =R h R +mg 例4：如图8—4所示，质点自倾角为α的斜面上方定点O沿光滑的斜槽从静止开始下滑，为使质点在最短时间内从O 点到达斜面，斜槽与竖直方向的夹角β应等于多少？解析：如图8—4甲所示，以经过O 点的竖直线上的一点O ′ 为圆心，OO ′ 为半径作圆，并使该圆与斜面恰好相切于A 点，与OO ′延长线交于B 点。

作图法解题【专题导引】用作图的方法把应用题的数量关系表示出来，使题意形象具体，一目了然，以便较快地找到解题的途径，它对解答条件隐蔽、复杂疑难的应用题，能起化难为易的作用。

在解答已知一个数或者几个数的和差、倍差及相互之间的关系、求其中一个数或者几倍数问题等应用题时，我们可以抓住题中给出的数量关系，借助线段图进行分析，从而列出算式。

【典型例题】【例1】五（1）班的男生人数和女生人数同样多。

抽去18名男生和26名女生参加合唱队后，剩下的男生人数是女生的3倍。

五（1）班原有男、女生多少人？【试一试】1、两根电线一样长，第一根剪去50厘米，第二根剪去180厘米后，剩下部分，第一根是第二根长度的3倍。

这两根电线原来共长多少厘米？2、甲、乙两筐水果个数一样多，从第一筐中取出31个，第二筐中取出19个后，第二筐剩下的个数是第一筐的4倍。

原来两筐水果各有多少个？【例2】两根电线共长59米，如果第一根电线剪去3米后，第一根电线的长度就是第二根的3倍，求原来两根电线各多少米？【试一试】1、甲、乙两筐苹果共重83千克，如果从甲筐取出3千克后，甲筐苹果的重量就是乙筐的4倍，甲、乙两筐苹果原来各重多少千克？2、学校图书馆共有科技书和故事书250本，又买来50本科技书后，科技书的本数是故事书的2倍，学校图书馆原来各有科技书和故事书多少本？【例3】甲、乙、丙、丁四个小组的同学共植树45棵，如果甲组多植2棵，乙组少植2棵，丙组植的棵数扩大2倍，丁组植树棵数减少一半，那么四个组植的棵数正好相同。

原来四个小组各植树多少棵？【试一试】1、甲、乙、丙、丁四个数的和是100，甲数加上4、乙数减去4、丙数乘以4、丁数除以4后，四个数就正好相等。

求这四个数。

2、甲、乙、丙三人分113个苹果，如果把甲分得个数减去5、乙分得的个数减去24、丙把分得的个数送给别人一半后，三人的苹果个数就相同。

三人原来各分得苹果多少个？【例4】五（1）班全体同学做数学竞赛题。

五年级奥数讲义：作图法解题图形具有直观性，用作图的方法可以将复杂应用题的数量关系直观地表示出来，使题目的已知条件和所求问题一目了然，并借助直观的图形进行分析、推理，进而很快找到解决问题的策略.这种方法我们称为作图法解题，特别是对解答条件复杂、数量关系不明显的应用题，能起到化难为易的作用.例题选讲例1:鸡与兔同笼共100只，一共有240只脚鸡与兔各多少只?【分析与解答】这是鸡兔同笼问题，我们在前几讲已学会用其它方法解答，现在用作图法来解答，让同，学们体会一下这种方法的作用.图1中两个长方形的总面积表示的是鸡与兔脚的总个数，宽表示每只鸡与兔的脚的个数.则长就是要求的鸡与兔的只数.仔细观察图2，阴影部分的面积表示鸡与兔多出的脚，它应该等于总面积减空白面积，即240—2 x 100=40(只)，那么阴影部分的长，也就是兔的只数应为40÷(4—2)=20(只)，鸡的只数就是1OO-20=80(只)．例2:甲、乙两车同时从A、B两地相向开出，第一次相遇时离A地有90千米，然后各按原速度继续行驶，到达目的地后立即沿原路返回，第二次相遇时离B地70千米处，求A、B两地的路程.【分析与解答】求A、B两地的路程，题中既没有给出甲、乙的速度，也没有给出相遇时间，解答比较困难.下面我们借助线段图来帮助分析.从图上可以看出，甲、乙两车从出发到第一次相遇共行驶了一个全程，当两车共行驶1个全程时，甲车行驶了90千米.从第一次相遇到第二次相遇，甲、々两车又共行驶了2个全程.因此从出发到第l二次相遇甲、乙两车共行驶了3个全程，那么甲车就行驶了3个90千米，即90×3=270千米，而甲车比全程多行70千米.所以A、B的距离为270—70=200(千米).练习与思考1.有10分和20分的邮票共18张，总面值为2．80元.请问：10分和20分的邮票各有几张?2.张红与李明同时从甲、乙两地相向而行，第一次两人相遇时离乙地400米.然后两人继续步行，各自到达目的地后立即返回，第二次相遇时离甲地200米，求甲、乙两地的距离.3.两根同样长的电线,第一根用去60 米，第二根用去20米，剩下的电线，第二根的长度是第一根的3倍.问：原来两根电线各长多少米?(先画图再列式计算)4.在一个除法算式里，被除除以除数商是25，余数是10，已知被除数、除数、商与余数的和是357，除数是多少?5.甲、乙、丙、丁四个数，甲、乙、丙三个数的总和是300，丁数比甲、乙、丙、丁四个数的平均数少30，求丁数.6.甲、乙两车同时从A、B两地相向而行，第一次相遇时离A地50千米，相遇后继续按原速度行完全程，到达目的地后返回，第二次相遇时离A地25千米.问：A、B两地距离是多少千米?7.一辆汽车从甲地开往乙地，往返共用20小时，去时用的时间是回来时的1．5倍，去时的速度比回来的速度每小时慢12千米.问：往返共行了多少千米?8.某单位买单价分别为70元、30元、20元的高、中、低三档皮包共47个，共用了2120元，其中每个30元的中档皮包个数是每个20元的低档包个数的2倍.问：三种皮包各买了多少个？。

第2讲画图法解应用题一、知识梳理在解答一些应用题时，用作图法可以把题目的数量关系揭示出来，使题意形象具体，一目了然，从而有助于快速找到解题的途径。

作图法解题可以画线段图，也可以画示意图，对解答条件隐蔽，复杂疑难应用题，能起到化难为易的作用。

例如在解答和差、和倍和差倍三类问题时，都可以用画图法表示。

二、例题精讲【例1】哥弟俩共有邮票70张，如果哥哥给弟弟4张邮票，这时哥哥还比弟弟多2张。

哥哥和弟弟原来各有邮票多少张？分析：由已知条件“哥哥给弟弟4 张后，还比弟弟多2 张”画图如下，可知哥哥的邮票比弟弟多4×2＋2＝10 （张）。

解：弟弟有邮票：（70－10）÷2=30 张，哥哥有邮票：30+10=40 张。

答：弟弟有邮票30张，哥哥有邮票40张。

练习1一个两层书架共放书72本，若从上层中拿出9本给下层，上层比下层多4本。

上、下层各放书多少本？【例2】果园里有桃树、梨树、苹果树共146棵。

桃树比梨树少7棵，苹果树比桃树多4棵，三种树各有多少棵？分析：先用线段图表示出三种树棵数之间的关系：从图上可以看出，梨树的棵数比桃树多7棵，苹果树的棵数比桃树多4棵，假设移动多的棵数，则两种果树共减少了7＋4=11（棵），相应的总棵数就减少11棵：146－11=135（棵），而135棵对应的就是桃树棵数的3倍。

解：桃树：（146－7－4）÷3=45（棵），梨树：45+7=52（棵），苹果树：45+4=49（棵）。

答：桃树有45棵，梨树有52棵，苹果树有49棵。

练习2 张明用272元买了一件上衣，一顶帽子和一双鞋子。

上衣比鞋贵60元，鞋比帽子贵70元。

求上衣、鞋子和帽子各多少钱？【例3】某公司三个厂区共有员工1900人，甲厂区的人数是乙厂区的2倍，乙厂区比丙厂区少300人，三个厂区各有多少人？分析：先用线段图表示出三厂区人数之间的关系：从图上可以看出，假设丙厂人数减少300人，总人数也减少300人，为1900－300=1600（人），此时总人数恰好是乙厂的4倍。

六年级用作图法解分数应用题(总11页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第1讲作图法解题（1）专题简析把一根铁条插入水沟，插在泥中的部分为05.米，露出水面的部分占铁条全长的12，水中的部分比全长的14少01.米，这根铁条全长多少米？举一反三1、一根竹竿露出水面2米，泥中部分占全长的25，水中部分比泥中部分多1米。

这根竹竿全长多少米？2、3、4、一根铁条插入水沟中，泥中部分占全长的16，水中部分比泥中部分少05.米，露出水面45.米。

这根铁条全长多少米？5、6、7、一辆小汽车从甲地开往乙地，已经行驶了全程的25还多35千米，这时剩下的路程占全程的14。

小汽车已经行驶了多少千米？8、9、典型例题2（限时15分钟）一桶油，倒出总量的30%少4千克后，还剩32千克，这桶油原来的质量是多少千克？举一反三1、一桶油倒出总量的40%少5千克后，还剩26千克，这桶油原来的质量是多少千克？2、有一袋大米，吃了它总量的12还多05.千克后，袋中还剩大米12千克，这袋大米原来的质量是多少千克？3、有汽油和柴油各一桶，汽油比柴油多450毫升，当汽油用掉12时，比柴油少50毫升，汽油和柴油原来各多少毫升？4、5、典型例题3（限时15分钟）甲、乙、丙三个建筑队共同修一条长900米的路，完工时知道甲队完成的1 2是乙队完成的13，是丙队完成的14。

这三个建筑队各修了多少米？举一反三1、小猴全家摘了220个桃子，小猴吃的个数的12是猴妈妈的14，是猴爸爸的15。

小猴吃了多少个桃子？2、3、4、有120个皮球分给三个班，一班分到的13是二班分到的12，是三班分到的15，三班分到多少个皮球？5、6、3、一个三层书架上共放了320本书，其中上层所放书数量的25，是中层所放书数量的27，是下层所放书数量的12。

这三层各放了多少本书？典型例题4（限时15分钟）某校六（1）班有学生46人，六（2）班比全年级人数的13多2人，这两个班人数的和共占全年级人数的57，六年级共有学生多少人？举一反三1、水果店运来一批水果，已知苹果有100千克，梨比水果总量的14多8千克，苹果和梨一共占这批水果的512。