分子动理论 气体分子平均动能
- 格式:ppt
- 大小:553.00 KB
- 文档页数:10

分子热运动理论与气体的平均动能计算方法分子热运动理论是描述气体分子运动规律的理论模型。
根据这一理论,气体分子以高速不规则运动,并具有随机的碰撞,从而产生了气体的性质。
通过分子热运动理论,可以计算出气体的平均动能。
本文将介绍分子热运动理论的基本原理,并详细讨论气体平均动能的计算方法。
一、分子热运动理论的基本原理分子热运动理论是基于统计物理学的原理,通过对大量气体分子运动的统计分析,得出了一系列关于气体性质的理论结论。
它的基本假设包括:1. 气体分子是微观粒子,其直径远小于气体容器的尺寸;2. 气体分子之间相互碰撞,碰撞时没有能量的损失;3. 气体分子之间相互碰撞是完全随机的;4. 气体分子的运动速度符合高斯分布。
根据这些基本假设,分子热运动理论推导出了许多关于气体性质的数学表达式,其中包括气体的平均动能计算方法。
二、气体的平均动能计算方法气体的平均动能是指气体分子的平均动能,可以表示为气体分子速度平方的平均值。
根据分子热运动理论,可以通过下列公式来计算气体的平均动能:平均动能 = (1/2)m·v²其中,m是气体分子的质量,v是气体分子的速度。
对于单原子气体,每个气体分子只有一个质点,其动能只有平动动能,由此可得出公式:平均动能 = (3/2)kT其中,k是玻尔兹曼常数,T是气体的绝对温度,单位均为国际单位制(SI单位制)。
对于多原子气体,由于分子能够既有平动动能又有转动动能,在计算平均动能时需要考虑这两部分动能的贡献。
根据分子热运动理论,可以将多原子气体的平均动能计算分为两个部分:1. 平动动能的计算:平动动能 = (3/2)kT该部分动能是由气体分子的平动运动引起的,与分子的转动无关。
2. 转动动能的计算:对于涉及转动的分子,转动动能可以表示为:转动动能 = (1/2)Iω²其中,I是转动惯量,ω是分子的角速度。
通过将平动动能和转动动能相加,即可得出多原子气体的平均动能。

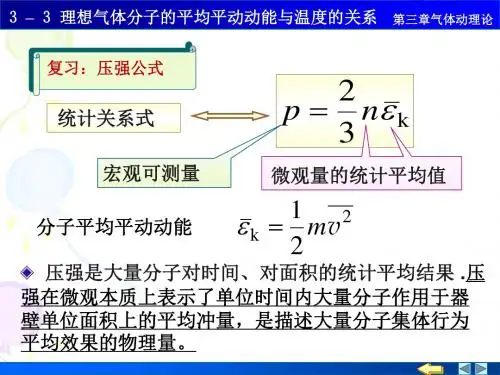
气体分子平均平动动能大小的量度
平均平动动能:ε=3kT/2。
其中:玻尔兹曼恒量k=1.38×10^-23J/K,T是人力学温标,换算关系为T(K)=t(℃)+273.15。
气体的温度是分子平均平动动能的量度是正确的。
从气体动理论的观点来看,理想气体是最简单的气体,其微观模型有三条假设:
1、分子本身的大小比分子间的平均距离小得多,分子可视为质点,它们遵从牛顿运动定律。
2、分子与分子间或分子与器壁间的碰撞是完全弹性的。
3、除碰撞瞬间外,分子间的相互作用力可忽略不计,重力的影响也可忽略不计。
因此在相邻两次碰撞之间,分子做匀速直线运动。
单个分子在一次碰撞中对器壁上单位面积的冲量。

气体平均平动动能公式和分子平均平动动能气体是由大量分子组成的物质,这些分子不断地做无规律的热运动。
在热学中,我们常常关注气体内部的平均平动动能,这对于研究气体性质和行为具有重要意义。
本文将从气体平均平动动能公式和分子平均平动动能两个方面展开讨论。
一、气体平均平动动能公式1.1 动能的定义在物理学中,动能是描述物体运动状态的物理量,它与物体的质量和速度有关。
对于气体内部的分子而言,它们具有的平均平动动能可以通过以下公式来表示:\[KE_{avg} = \frac{3}{2} kT\]其中,\(KE_{avg}\)表示气体分子的平均平动动能,\(k\)是玻尔兹曼常数,\(T\)是气体的绝对温度。
1.2 推导过程这个公式的推导过程可以通过统计力学的方法进行。
由分子动能定理可知,一个分子的平均平动动能大小与温度成正比。
而对于气体而言,由于分子具有三个独立的平动方向,因此气体分子的平均平动动能为3kT。
气体内部所有分子的平均平动动能可以表示为3kT的总和,即\(KE_{avg} = \frac{3}{2} kT\)。
1.3 公式意义这个公式的意义在于,它揭示了气体分子的平均平动动能与温度之间的关系。
从宏观角度来看,气体的温度越高,分子的平均平动动能就越大,这也说明了温度对气体热运动的影响。
二、分子平均平动动能2.1 分子速度的分布气体分子的速度分布是描述气体分子热运动状态的重要物理量。
根据麦克斯韦-玻尔兹曼分布律,气体分子在热平衡状态下的速度分布可以用以下公式来表示:\[f(v) = \sqrt{\frac{m}{2\pi kT}} e^{-\frac{mv^2}{2kT}}\]其中,\(f(v)\)表示速度为\(v\)的分子的概率密度函数,\(m\)为分子的质量,\(k\)为玻尔兹曼常数,\(T\)为气体的绝对温度。
2.2 分子平均平动动能气体分子的平均平动动能可以通过速度分布函数来进行求解。
根据统计力学的理论,气体分子的平均平动动能可以表示为:\[KE_{avg} = \int_0^\infty \frac{1}{2}mv^2 f(v) dv\]将速度分布函数带入上式,可以得到气体分子的平均平动动能。

第六章 分子动理论6-1 一立方容器,每边长20cm 其中贮有,的气体,当把气体加热到时,容器每个壁所受到的压力为多大?解:根据理想气体状态方程NkT pV =得11kT Vp N =。
所以 6-2 一氧气瓶的容积是,其中氧气的压强是,规定瓶内氧气压强降到时就得充气,以免混入其他气体而需洗瓶,今有一玻璃室,每天需用氧气,问一瓶氧气能用几天。
解:一瓶氧的摩尔数为RT pV =ν,用完后瓶中还剩氧气的摩尔数为RTVp '='ν,实际能用的摩尔数为RTp p )(-'-='=ννν∆.每天所用氧气的摩尔数为RT V p ''''=''ν。
一瓶氧气能用的天数为6-3 有一水银气压计,当水银柱为0.76m 高时,管顶离水银柱液面0.12m ,管的截面积为2.0×10-4m 2,当有少量氦(He)混入水银管内顶部,水银柱高下降为0.6m ,此时温度为27℃,试计算有多少质量氦气在管顶(He 的摩尔质量为0.004kg ·mol -1)?解:当压强计顶部中混入氦气,其压强为)(21h h g p -=ρ,由理想气体状态方程得氦气的质量为6-4 在常温下(例如27℃),气体分子的平均平动能等于多少ev?在多高的温度下,气体分子的平均平动能等于1000ev?解:23.8810ev -⨯ ,301K6-5 计算下列一组粒子平均速率和方均根速率?21 4 6 8 210.0 20.0 30.0 40.0 50.0 解:s /m 7.2141.5020.4080.3060.2040.1021=⨯+⨯+⨯+⨯+⨯=υ 6-6 下列系统各有多少个自由度: (1)在一平面上滑动的粒子;(2)可以在一平面上滑动并可围绕垂直于平面的轴转动的硬币; (3)一弯成三角形的金属棒在空间自由运动.解:(1)确定平面上运动的粒子需要2个独立坐标,所以自由度数为2;(2)确定硬币的平动需要两个独立坐标,确定转动需要一个坐标,确定硬币位置共需3个坐标,所以自由度数为3;(3)这是一个自由刚体,有6个自由度,其中3个平动自由度和3个转动自由度。

第三章 分子动理论通过复习后,应该:1.掌握理想气体物态方程、压强公式、能量公式、混合气体的分压强、表面张力、弯曲液面的附加压强、毛细管中液面的变化;2.理解分子力、理想气体的微观模型、玻尔兹曼分布定律、气体的溶解、毛细现象、接触角;3.了解麦克斯韦速率分布定律、气体栓塞、肺泡的吸气和稳定。
3-1 一容器用隔板分成相等的两部分,一边装CO 2 ,另一边装H 2 ,两边气体的质量相同,温度相同。
如果隔板与容器壁间无摩擦,隔板是否会移动?为什么?答: 根据理想气体状态方程RTμpV M =,可得RTμVp M =。
因容器两部分气体的质量M 、体积V 、温度T 相同,R 是常数,只有摩尔质量μ不同,所以容器两部分的压强不同,隔板会移动。
由于H 2 的摩尔质量小于CO 2 的摩尔质量,故H 2 一侧的压强大于CO 2 ,隔板会向CO 2 一侧移动。
3-2 两瓶不同种类的气体,设分子平均平动动能相同,但气体的分子数密度不同,问它们的温度是否相同?压强是否相同?答: 根据分子平均平动动能公式kT 23=ε,当分子平均平动动能ε相同时,两瓶气体的温度相同。
根据压强公式εn p 32=,当分子平均平动动能ε相同而分子数密度n 不同时,压强不相同。
3-3 在容积为40L 的贮气筒内有112g 氮气,当贮气筒的温度为27℃时,筒内氮气的压强为多少个大气压?分子数密度又是多少?解: 已知V =40L=4×10-2m 3,T =(27+273)K=300K ,μ=2.8×10-2kg·mol -1,M =112g=0.112kg ,R =8.31J·mol -1·k -1 ,根据气态方程RT μpV M=可得筒内氮气的压强为RT μVp M==522105.2104108.230031.8112.0⨯=⨯⨯⨯⨯⨯-- 2.47atm Pa = 其分子数密度为252223100.6104108.210022.6112.01⨯=⨯⨯⨯⨯⨯=⋅==--V N M V N n A μ-3m3-4 某氧气瓶的容积是35L ,瓶内氧气的压强为1.5×107Pa ,给病人输一段时间氧气后,氧气的压强降为1.2×107Pa ,设温度为20℃,求这段时间内用去氧气的质量。

气体的分子速率与平均动能计算气体是由大量分子组成,分子以高速不规则运动着。
本文将探讨气体分子的速率以及如何计算气体的平均动能。
一、气体分子的速率气体分子的速率是指分子在气体中运动的速度。
根据动理论,气体分子的速率服从Maxwell-Boltzmann速度分布曲线。
Maxwell-Boltzmann速度分布曲线描述了不同速率下分子数的分布情况。
为了更好地理解气体分子的速率分布,我们可以引入分子平均速率的概念。
分子平均速率是指所有分子速率的平均值,可以通过以下公式计算:平均速率 = 总速率 / 分子数其中,总速率是所有分子速率的总和,分子数是气体中的分子总数。
通过计算分子平均速率,我们可以更好地描述气体分子的运动情况。
二、气体分子的平均动能气体分子的平均动能是指同一温度下的气体分子平均的动能大小。
根据动理论,气体分子的动能与其速率有关。
分子的动能可以通过以下公式计算:动能 = 1/2 * m * v^2其中,m是分子的质量,v是分子的速率。
通过计算所有分子的动能,并求其平均值,就可以得到气体分子的平均动能。
三、气体的平均动能计算示例假设我们有一瓶装有氢气(H2)的容器,温度为300K。
我们可以通过以下步骤计算气体分子的平均动能:1. 确定氢气分子的质量。
根据元素周期表,氢的相对原子质量为1。
由于氢气分子由两个氢原子组成,因此氢气的相对分子质量为2。
2. 计算气体分子的速率。
根据Maxwell-Boltzmann速度分布曲线,我们可以获得不同速率下分子数的分布情况。
然后,根据公式计算分子平均速率。
3. 计算气体分子的动能。
根据上述公式,将氢气分子的质量和速率代入,计算每个分子的动能。
然后,求得所有分子动能的总和。
4. 计算气体分子的平均动能。
将总动能除以分子数,即可得到气体分子的平均动能。
通过以上步骤,我们可以计算出气体分子在给定温度下的平均动能。
结论本文讨论了气体分子速率与平均动能的计算方法。
了解气体分子的速率分布以及平均动能有助于我们更好地理解气体分子的性质和行为。
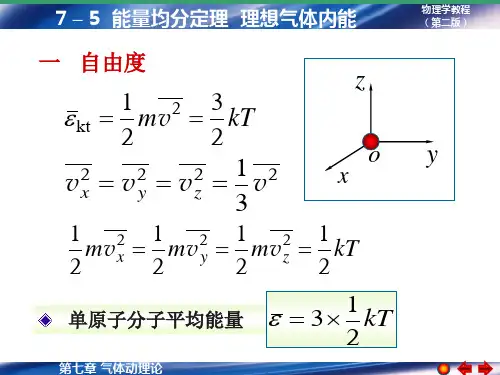
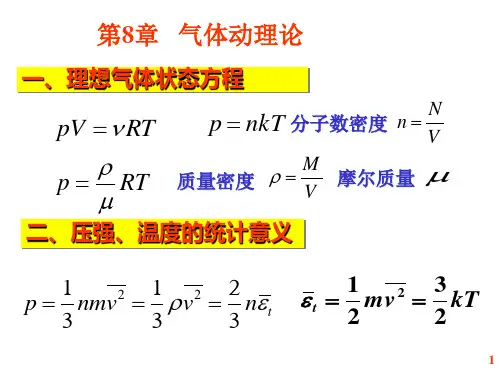

气体的平均分子动能全文共四篇示例,供读者参考第一篇示例:气体的平均分子动能是指气体中各个分子具有的平均动能值。
在气体分子间距离较大,分子运动自由度较高的情况下,我们可以通过统计力学的方法计算出气体分子的平均动能值。
根据动能定理,气体分子的平均动能与其运动状态有关,其表达式如下:\[\langle K \rangle = \frac{1}{2} kT\]\langle K \rangle为气体分子的平均动能,k为玻尔兹曼常数,T 为气体的绝对温度。
这个式子告诉我们,气体分子的平均动能与温度成正比,即温度越高,气体分子的平均动能也越大。
气体的平均分子动能与气体的温度有着密切的关系。
当气体的温度升高时,气体分子的平均动能也会增加,因为温度的升高会导致气体分子的热运动更加剧烈。
这就是为什么我们在高温下感觉到气体分子的活动更加激烈的原因。
而根据气体动理论的假设,所有气体分子具有相同的动能,这意味着气体分子的平均动能是相等的。
在现实情况下,气体分子之间的碰撞会导致它们的动能发生变化,使得气体分子的平均动能存在一定的分布。
但在一定范围内,我们仍然可以用平均动能来描述气体分子的运动状态。
在气体分子的平均动能范围内,我们可以通过动能定理来计算气体的一些性质。
气体的压强与气体分子的平均动能有密切的关系。
根据理想气体的状态方程,气体分子的平均动能与气体的压强成正比。
这说明,气体分子的平均动能越大,气体的压强就越大。
气体的平均分子动能是描述气体分子运动状态的重要参数。
通过研究气体分子的平均动能,我们可以深入了解气体的性质和行为,为研究气体的热力学性质和动力学过程提供有力支持。
希望通过这篇文章的介绍,读者对气体的平均分子动能有了更深入的了解。
第二篇示例:气体是由大量分子组成的物质,在热力学中,我们常常会研究气体的平均分子动能。
气体的平均分子动能是指气体分子在运动过程中所具有的平均动能。
它与气体的温度和分子质量有关,是研究气体热力学性质的重要参数。

气体分子的速率与气体分子的平均动能的计算气体分子的速率与其平均动能是物理学中研究气体性质的重要指标。
本文将介绍如何计算气体分子的速率和平均动能,并探讨其在相关领域的应用。
一、气体分子的速率计算气体分子的速率指的是分子在三维空间中的运动速度。
根据动能定理,气体分子的平均速率可以通过动能与质量的关系来计算。
设某气体分子的质量为m,速率为v,则其动能E与速率v满足以下关系:E = 1/2mv^2其中,E为气体分子的动能。
对于一组具有不同速率的气体分子,可以通过测量其速度分布来获得速率的统计值。
常用的方法是通过测量气体分子的平均速率(平均动能)来描述气体的动力学特性。
二、气体分子的平均动能计算气体分子的平均动能是指在一定温度下,气体分子的动能的平均值。
根据动能定理,气体分子的平均动能与温度有关。
通过玻尔兹曼常数k (k≈1.38×10^-23 J/K)和温度T来计算平均动能E_avg的公式如下:E_avg = (3/2)kT其中,E_avg表示气体分子的平均动能,T表示气体的温度。
平均动能的计算可以帮助我们了解气体的热学性质和动态特性。
通过比较不同气体在相同温度下的平均动能,我们可以进一步研究气体分子的行为和相互作用。
三、速率与平均动能的应用气体分子的速率和平均动能的计算在多个领域有着广泛的应用,以下列举其中几个方面:1. 热学性质研究:通过计算气体分子的平均动能,能够得出气体在不同温度下的热学性质,如热容、热膨胀等,从而为相关领域的热学实验和工程应用提供理论依据。
2. 化学反应速率研究:气体分子速率的计算对于研究化学反应速率有着重要的意义。
通过研究气体分子在不同温度下的速率分布,可以预测反应速率的变化规律,从而提高化学反应的效率和控制。
3. 材料科学中的应用:气体分子速率的计算可以帮助研究气体在材料中的渗透性和扩散性。
这对于开发新的气体分离和传输技术、制备新型材料等方面具有重要意义。
四、总结本文介绍了气体分子速率与平均动能的计算方法,并探讨了其在相关领域的应用。
气体分子的平均平动动能气体分子的平均平动动能可以根据理想气体状态方程和分子动理论进行推导。
首先,我们先来回顾一下理想气体状态方程:PV = nRT其中,P表示气体的压强,V表示气体的体积,n表示气体的物质的量,R为气体常数,T表示气体的温度。
在分子动理论中,气体被认为是由大量微观分子组成的,分子具有质量m和速度v。
根据分子动理论,我们可以得到气体分子的平均平动动能的表达式。
首先,根据动能定理,一个物体的动能可以表示为其质量和速度的平方的乘积的一半。
因此,气体分子的平均平动动能可以表示为:KE_avg = (1/2) m v^2同时,根据分子动理论,气体分子的速度和温度之间存在着直接的关系。
具体来说,根据麦克斯韦尔-玻尔兹曼速率分布定律,分子速度的分布满足麦克斯韦尔-玻尔兹曼速率分布函数:f(v) = 4π (m/2πkT)^(3/2) v^2 exp(-mv^2/2kT)其中,f(v)表示速度为v的分子的比例,m为分子质量,k为玻尔兹曼常数,T为温度。
由于分子速度的平方与动能直接相关,所以我们可以将速率分布函数转化为动能分布函数,得到动能分布函数的表达式。
首先,我们假设动能为E的分子与速度为vE的分子的比例为f(E),则有:f(E) = (4π (m/2πkT)^(3/2) / vE^2) exp(-E/kT)接下来,我们对动能分布函数进行积分,得到分子平均动能的表达式。
KE_avg = ∫ E f(E) dE= ∫ (4π (m/2πkT)^(3/2) / vE^2) E exp(-E/kT) dE= (4π (m/2πkT)^(3/2)) ∫ E^2 exp(-E/kT) dE / ∫ E exp(-E/kT) dE由于上述积分不太好求解,我们可以利用近似方法来简化计算。
一种常用的近似方法是利用玻尔兹曼分布函数的性质,在该分布下,分子动能的平均值与温度成正比,即:KE_avg = (3/2) kT结合理想气体状态方程 PV = nRT,我们可以将分子平均动能表达式进一步转化为:KE_avg = (3/2) (PV/n)通过以上推导,我们得到了气体分子的平均平动动能的表达式。
第一节 分子动理论【要点归纳】一、物体是由大量分子组成的一、分子的大小:1.分子直径的数量级为10-10 m.2.分子体积的数量级一般为10-29 m 3.3.分子质量的数量级一般为10-26 kg. 二、阿伏加德罗常数:1.定义:1 mol 的任何物质都含有相同的粒子数,这个数量可以用阿伏加德罗常数来表示.2.数值:阿伏加德罗常数常取N A =6.02×1023mol -1,粗略计算中可取N A =6.0×1023mol -1.3.意义:阿伏加德罗常数是一个重要常数.它把摩尔质量、摩尔体积这些宏观物理量与分子质量、分子的大小等微观物理量联系起来了,即阿伏加德罗常数N A 是联系宏观世界与微观世界的桥梁.4.宏、微观物理量与阿伏加德罗常数间的关系(1)已知固体和液体(气体不适用)的摩尔体积V mol 和一个分子的体积v ,则N A =V mol v;反之亦可估算分子的大小. (2)已知物质(所有物质,无论液体、固体还是气体均适用)的摩尔质量M 和一个分子的质量m ,则N A =M m;反之亦可估算分子的质量. (3)已知物体(无论固体、液体还是气体均适用)的体积V 和摩尔体积V mol ,则物体含有的分子数n =V V mol N A =M ρV mol N A.其中ρ是物质的密度,M 是物质的质量. (4)已知物体(无论液体、固体还是气体均适用)的质量和摩尔质量,则物体含有的分子数n =M mN A . (5)分子体积v =V m N A =M m ρN A .如果把分子简化成球体,可进一步求出分子的直径d =36v π=36MmρN Aπ三、估算气体分子间的距离气体分子间的间隙不能忽略,设想气体分子平均分布,且每个气体分子平均占有的空间设想成一个小立方体,气体分子间的距离就等于小立方体的边长,如图所示.每个空气分子平均占有的空间体积v′=v mN A=M mρN A,分子间的距离a=3v′.二、分子热运动一、扩散现象:1.定义:不同的物质互相接触,过一段时间后物质分子会彼此进入对方,这一现象称为扩散,扩散是一种常见的物理现象.如在房间的一角撒上香水,整个房间都能闻到香味;金块和铅块压紧在一起,放置足够长的时间,会发现铅中有金,金中有铅等,都是扩散.2.产生原因:是由物质分子的无规则运动产生的.3.特点:(1)在气体、液体、固体中均能发生,而气体的扩散现象最明显.(2)扩散快慢与温度有关,温度越高,扩散越快,表明温度越高,分子运动越剧烈.(3)从浓度大处向浓度小处扩散,且受“已进入对方”的分子浓度的限制,当进入对方的分子浓度较低时,扩散现象较为显著.二、布朗运动1.定义:布朗运动是悬浮在液体中的固体微粒的无规则运动,是在显微镜下观察到的.2.布朗运动的三个主要特点:微粒在永不停息地做无规则运动;颗粒越小,布朗运动越明显;温度越高,布朗运动越明显.3.产生布朗运动的原因:由于液体分子无规则运动对固体微小颗粒各个方向撞击的不均匀性所造成.4.影响布朗运动的因素:微粒的大小和液体(或气体)温度的高低.(1)微粒越小,布朗运动越明显.(2)温度越高,布朗运动越激烈.5.布朗运动与分子热运动的关系(1)布朗运动是无规则的――→反映分子运动是无规则的;(2)布朗运动是永不停息的――→反映分子运动是永不停息的;(3)温度越高,布朗运动越激烈――→反映温度越高,分子的运动越激烈.三、分子间的作用力 1.分子间有空隙(1)气体分子的空隙:气体很容易被压缩,表明气体分子间有很大的空隙.(2)液体分子间的空隙:水和酒精混合后总体积会变小,说明液体分子间有间隙.(3)固体分子间的空隙:压在一起的金片和铅片,各自的分子能彼此进入到对方的内部说明固体分子间也存在着空隙.2.分子间的作用力(1)分子间同时存在着相互作用的引力和斥力.分子间实际表现出的作用力是引力和斥力的合力.(2)分子间作用力与分子间距离变化的关系(如图所示):分子间的引力和斥力都随分子间距离r 的增大而减小,随分子间距离的减小而增大.但斥力比引力变化得快.(3)平衡位置:我们把分子间距离r =r 0时,引力与斥力大小相等,分子力为零.分子间距离等于r 0(数量级为10-10m)的位置叫做平衡位置.(4)分子间的引力和斥力随分子间距离r 的变化关系分子间的引力和斥力都随分子间距离r 的增大而减小,但斥力减小得更快.F 随r 变化的关系如图:当r <r 0时,合力随距离的增大而减小;当r >r 0时,合力随距离的增大先增大后减小. ①当r =r 0时,F 引=F 斥,F =0.②当r<r 0时,F 引和F 斥都随分子间距离的减小而增大,但F 斥增大得更快,分子力表现为斥力.③当r>r0时,F引和F斥都随分子间距离的增大而减小,但F斥减小得更快,分子力表现为引力.④当r≥10r0(10-9m)时,F引和F斥都十分微弱,可认为分子间无相互作用力(F=0).四、分子动理论1.分子动理论内容:物体是由大量分子组成的,分子在永不停息地做无规则运动,分子之间存在着引力和斥力.2.根据分子力说明物体三态不同的宏观特征分子间的距离不同,分子间的作用力表现也就不一样.(1)固体分子间的距离小,分子之间的作用力表现明显,分子只能在平衡位置附近做范围很小的无规则振动.因此,固体不但具有一定的体积,还具有一定的形状.(2)液体分子间的距离也很小,分子之间的作用力也能体现得比较明显,但与固体分子相比,液体分子可以在平衡位置附近做范围较大的无规则振动,而且液体分子的平衡位置不是固定的,在不断地移动,因而液体虽然具有一定的体积,却没有固定的形状.(3)气体分子间距离较大,彼此间的作用力极为微小,可认为分子除了与其他分子或器壁碰撞时有相互作用外,分子力可以忽略.因而气体分子总是做匀速直线运动,直到碰撞时才改变方向.所以气体没有一定的体积,也没有一定的形状,总是充满整个容器.五、气体分子运动的特点气体分子运动的“三性”1.自由性:由于气体分子间的距离比较大,大约是分子直径的10倍左右,分子间的作用力很弱,因此除了相互碰撞或者跟器壁碰撞外,不受力而做匀速直线运动,因而气体能充满它所达到的整个空间.2.无序性:由于分子之间频繁地碰撞,每个分子的速度大小和方向频繁改变,分子的运动杂乱无章,在某一时刻向着任何一个方向运动的分子都有,而且向着各个方向运动的气体分子数目都相等.3.规律性:气体分子速率分布呈现出“中间多,两头少”的分布规律.当温度升高时,速率大的分子数增多,速率小的分子数减少,分子的平均速率增大.反之,分子的平均速率减小.如图所示。
分子的平均动能公式
根据热力学理论,分子的平均动能与其温度成正比,可以用下面的公
式表示:
E=3/2*k*T
其中,E表示分子的平均动能,k表示玻尔兹曼常数,T表示分子所
处的温度(以开尔文为单位)。
上述公式可以通过统计物理学的方法进行推导。
在理想气体模型中,分子的平均动能等于它们动能的平均值。
根据经
典力学理论,分子的动能可以表示为:
E=1/2*m*v^2
其中,m表示分子的质量,v表示分子的速度。
在理想气体模型中,假设气体分子的速度服从麦克斯韦速度分布。
根
据麦克斯韦速度分布函数,分子速度的分布概率与速度的平方成正比,即:f(v) = 4π * (m / (2πkT))^3/2 * v^2 * exp(-mv^2 / 2kT)
其中,f(v)表示分子速度的分布概率,exp(x)表示自然常数e的x次方。
将上述速度分布函数代入分子动能公式中
E = ∫ 1/2 * m * v^2 * f(v) * dv
对上式进行积分可以得到:
E=3/2*k*T
上述推导过程得到了分子的平均动能公式。
需要注意的是,以上推导基于理想气体模型和经典力学理论,在极端条件下,如低温、高压下,该公式的适用性可能会受到限制。
在这些情况下,可能需要考虑量子力学效应和能级结构对分子动能的影响。