制程能力分析方法介绍共22页文档

制程能力分析

C
pk
1 Ca

C
p
1. Cpk 與 |Ca| 呈反向； Cpk 與 Cp呈正向 2. Cpk 同時反應製程中心與規格中心的差距及製程變異的大小。
A
1-34
P D
C
Example 12
1. 優美家具桌面厚度規格為2±0.1cm，而製程中心u=2.05，σ=0.16/6，請計算Cpk 值。
A
1-3
P D
C
Natural tolerance
A
1-4
P D
C
A
1-5
P D
C
Sec 2. 自然公差與規格公差
Case 1： 6
USL LSL
A
1-6
P D
C
Case 2： 6
USL LSL
A
1-7
P D
C
Case 3： 6
USL LSL
A
1-8
P D
C
對於6 σ > (USL - LSL) 之解決途徑
Chatper 9
製程能力分析
A
1-1
P D
C
學習內容
1. 2. 3. 4. 5. 定義自然公差與規格公差製程能力指標以管制圖進行製程能力分析組件裝配公差
A
1-2
P D
C
Sec 1. 定義
1. 2. 3. 製程能力 (process capability)：製程產出的一致性的能力。生產能力 (production capability)：反應產出數量的能力。製程能力分析 (process capability analysis)：對製程能力的研究，以進行製程所產生變異性相對於產品規格之分析。 4. 產品特性分析 (product feature analysis)：只依據產品本身的相關數據進行品質特性分析，無從了解或分析製程狀態。 5. 自然公差 (natural tolerance)：在管制狀態下，製程中產品品質變異在六個標準差範圍內。 6. 規格公差 (specification tolerance)：規格上限 (upper specification limit, USL) 減規格下限 (lower specification limit, LSL)後的界限寬度。注意: UCL=upper control limit LCL=lower control limit

制程能力分析

單元目的在瞭解何謂「統計管制狀態」後，製程能力分析的目的是進一步使製程能符合顧客的需求，因為製程能力是指製程的一致性，而製程的變異可以用來衡量製程輸出之一致性，它可以用來協助製造前之開發活動﹑找出問題﹑設定標準與降低成本。

產品規格來自顧客的需求或設計者個人的專業學養，因此製程必須具有產出符合工程規零件的能力。

研究製程能力的意義在於決定製程的自然公差、協助設定製程標準和規格、以及確定和消除「非自然變異」。

單元大綱製程能力分析製程能力的評價製程能力的改善製程能力分析何謂製程能力製程能力是指「各種能力均標準化，製程在管制狀態下所呈現之質與量的能力」。

故製程能力可以產量、效率表示，也可以成品、半成品、零件等之品質特性來表示，也可以不良率或缺點數來表示。

製程能力可為一部機器或一設備在一定條件下操作的能力，前者一般稱為「機器能力」，可為一項預定的產品之全部製程，包括人、材料機器及方法在長時間內所程現的能力。

前者一般稱為「機器能力」，而後者則稱為「綜合製造能力」，後者經常包括了工具損耗之正長影響，材料的微些變化及其它的微小變化。

在此我們所討論之製程能力即以後者為主。

製程能力與規格當考量製程績效之前，必須先討論兩個重要的問題：1.製程是否有維持良好”統計管制狀態”的能力。

2.是否具有產出符合工程規格零件的製程能力。

只有當製程處於”統計管制狀態”下，估計製程能力才合理，因為當製程處於”統計管制狀態”下，製程沒有可歸咎的非自然因素存在，此時才可以顯示製程真正的變異。

此部份已於管制圖介紹中詳細介紹過。

製程是否具有產出符合工程規格零件的能力，在於製程變異範圍是否介於工程規格之內，一邊而言可能有下列三種情況：1.製程變異小於規格間差異。

2.製程變異等於規格間差異。

3.製程變異大於規格間差異。

第一種情況：6＜USL－LSL當製程變異(6)小於規格間之差(USL－LSL)時，這是最理想情況，如圖個別值分布A和規格的關係最佳，因為規格比製程變異大很多，即使製程平均值有很大的移動，也不易超出規格界線；分佈B的變異比分佈A大，但所有個別值仍在規格之內分佈C所顯示的變異更大，但仍在規格之內。

制程能力(Cpk)分析教程.

統計其頻數如下:
作其直方圖如下:
(二.直方圖的觀察与分析
(1對圖形形狀的分析:常見的直方圖有以下幾种
工程能力分析与控制
統計量与統計圖
4228272633291824321434223029222422284812429353630341442386283222253639241828163836212026208181237
¤À²Õ0~5
6~1011~1516~2021~2526~3031~3536~4041~4546~50 Ó¼Æ1236
10
10
8
7
2
1
1
2
3
6
10
10
8
7
2
1
系列2
正常型
偏向型孤島型雙峰型
1正常型
2孤島型:說明在短時間內有异常因素在作用,如原材料發生變化,有不熟練工人替班等.3偏向型:說明加工中心發生了偏移4雙峰型:是由產品混批造成的
式中K為偏移系數,其值為K=ε/T/2
ε為偏移量,其值為
第五章:工序能力分析
C P =T/6σ
C P =T/6α=T U -T L /6S
工程能力分析与控制
工序能力分析
工程能力分析与控制
工序能力分析
,,
,
重要差別.正常生產
低,誤差小
規律的圖形
123610108721
.
定的生產高,所加工
服從政態圍會增大至花費更大,用6σ來表
.
(二數据分類与數据整理
數据可分為計量值數据和計數值數据兩類:
計量值數据是可以連續取值的:如長度,重量,溫度等.
計數值數据是不可以連續取值的:如不合格品數,缺陷數等.

制程能力分析

制程能力分析緒言在產品生產周期內統計技朮可用來協助制造前之開發活動、制程變異性之數量化、制程變性相對于產品規格之分析及協助降低制程內之變異性。

這些工作一般稱為制程能力分析(process capability analysis)。

制程能力是指制程之一致性，制程之變異性可用來衡量制程輸出之一致性。

我們一般是將產品品質特性之6個標准差范圍當做是制程能力之量測。

此范圍稱為自然允差界限(natural tolerance limits)或稱為制程能力界限(process capability limits)。

圖9-1顯示品質特性符合常態分配且平均值為μ，標准差為σ之制程。

制程之上、下自然允差界限為UNTL=μ+3σ上自然允差界限LNTL=μ-3σ下自然允差界限對于一常態分配，自然允差界限將包含99.73%之品質數據，或者可說是0.27%之制程輸出將落在自然允差界限外。

如果制程數據之分配不為常態，則落在μ±3σ外之機率將不為0.27%。

(例) 產品外徑之規格為5±0.015cm，由樣本資料得知X=4.99cm，σ=0.004cm，試計算制程之自然允差界限。

(解): UNTL=4.99+3(0.004)=5.002LNTL=4.99-3(0.004)=4.978制程能力分析可定議為估計制程能力之工程研究。

制程能力分析通常是量測產品之功能參數而非制程本身。

當分析者可直接觀察制程及控制制程數據之收集時，此種分析可視為一種真的制程能力分析。

因為經由數據收集之控制及了解數據之時間次序性，可推論制程之穩定性。

若當只有品質數據而無法直接觀測制程時，這種研究稱為產品特性分析(product characterization)。

產品特性分析只可估計產品品質特性之分布，或者是制程之輸出(不合格率)，對于制程之動態行為或者是制程是否在管制內則無法估計。

這種性形通常是發生在分析供應商提供之品質數據或者是進貨檢驗之品質資料。

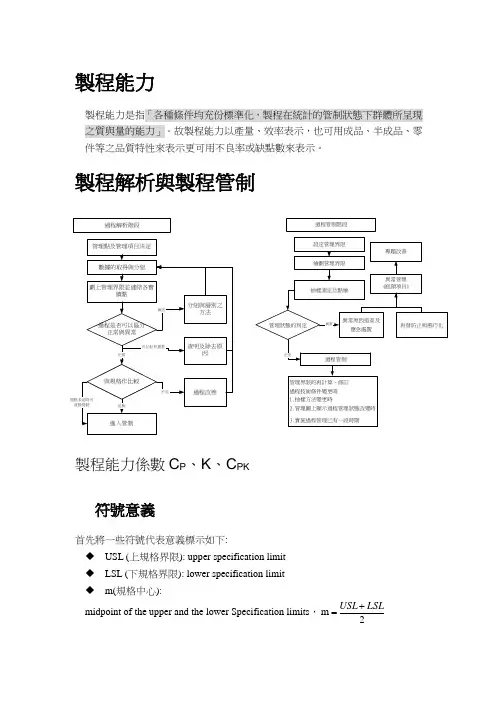
制程能力分析(SPC)

P.4 一種系統性工作。這種工作包括下列步驟: (1)確定能代表製程能力的品質特性。 (2)由製程抽取樣本,測定其特定性質,普通需搜集 30 個以上數据。 (3)點繪出統計的形態,計算平均值与標準差(利用次數分配圖)。 (4)解釋此種形態,發掘異常現象, 確定在經濟上是否值得採取措施。 (5)對異常現象採取措施。
P.18
5.3.綜合評價:
要製程能達到規格要求必須 K 与 C P 均好方可,但有時 K 雖很好,但 C P 不好,結果還會有不良品, 与 C P 兩者綜合起來評定等級。 5.3.1.CPK(CMK)計算:
CPK(CMK) = CP(1-K) = CP(1X-U T/2 X - LCL
P.15
5.2.工程能力數之評價:
設定工程上下限的目的,在於希望製造出來的各個的各個產品之特性值,能在規格上下限之容許範圍內,工程能力的評價之目的就在於衡量產品分散寬度符合公差的程度, 工程能力數又可稱為工程精密度指數 (Capablity Of Precision) .
規格公差 5.2.1.CP 之計算: CP = 6 個標準差 = 6σ T 或 CP = 6 v 容許差異
2.2. * 製程:指從事生產的机器、工具、方法、材料与人員(指 5M)等的一些獨立組合。 * 管制:指製程在統計管制狀態下亦即是毫無時間性的移動或其他可追溯的變異原因時,所得到產品均一性。
P.5
*能力:指根据測試的績效,用以獲得
可以測定的結果。我們請看以下圖形:
P.6
P.7
P.8
三〄製程能力分析之用途
製程能力分析之用途可分為以下几點: 3.1.提供資料給設計部門,使其能盡量利用目前之工程能力,以設計新產品。 3.2.決定一項新設備或翻修的設備能否滿足要求。 3.3.利用机械之能力安排適當工作,使其得到最佳應用。

制程能力解析

1. 問題列舉法 2. KJ 法 3. 5W1H 法 4. 7M 5. 5S
品管有效手法運用
1. QC工程圖 2. 品質管制圖 3. 系統圖 4. 矩陣 5. 日程計劃圖 6. 箭形作圖 7. 抽樣法
C. 補償系統
品管有效手法運用 D. 解析手法
1. 檢驗推定 2. 抽樣檢驗 3. 實驗計劃 4. 迴歸分析 5. 田口品質工程 6. IE方法
2、製程能力與製程績效
製程能力（Process Capability）：6σ 以6σ表示製程能力，其中σ為固有之變異（標準差）即導因於一般原因，用Rbar/d2來估計，所以又稱6σ為自然公差。
製程績效（Process Performance）： 6σ 亦以6σ表示製程績效，但其中σ乃由s（或 ^ σs）來估計，即導因於一般及特殊原因。
1) 異常現象的發現：制造條件查核表、自主檢查、品管員抽樣、管制圖、不良率高、故障頻繁或產量達不到要求。
2) 異常原因的追查：逆向追溯、順向追查、過程審查、4M法、層別法、改善提案、頭腦風暴、田口實驗計劃。
3) 異常連絡單：目的、內容及填寫方法。 4) 改正行動：應急措施、根本措施。
製程管制績效的整理與分析
結論
1. （變異）乃是過程的一部份 2. 進行企劃前必須先預測人事物未來可能的表現，
但任何測試（實驗）過去的績效表現；即使頗具價值還是無法作準。 3. 員工都在某一個自己控制不了的系統下工作，即使他們努力嘗試決定，績效表現的是（系統）而非（個人技能) 4. 唯有管理階層才能改變系統。 5. 某些員工的表現總在水準之上而某些總在水準之下。
）
3 、製程能力的評價
（8）綜合評價
x-M
Cpk=Cp（1-K）=CpD

制程能力分析

製程能力製程能力是指「各種條件均充份標準化，製程在統計的管制狀態下群體所呈現之質與量的能力」。

故製程能力以產量、效率表示，也可用成品、半成品、零件等之品質特性來表示更可用不良率或缺點數來表示。

製程解析與製程管制製程能力係數C P 、K 、C PK符號意義首先將一些符號代表意義標示如下:◆ USL (上規格界限): upper specification limit ◆ LSL (下規格界限): lower specification limit ◆ m(規格中心):midpoint of the upper and the lower Specification limits ，2m LSLUSL +=T (目標值): Target指定雙邊規格時 (1)準確度k()LSLUSL μ-m 2k C -==a ，-1≦k ≦1， (2)精密度C p 指標σ6LSLUSL C p -=(3)C pk 指標C pk 指標主要是用以衡量製程之實際成效(process performance)，而C pk 製程能力指標定義如下：⎭⎬⎫⎩⎨⎧--=σμσμ3,3USL LSL Min C pk ，或C pk =(1-k )C p指定單邊規格時T (目標值): Target ，如果沒有目標值時，則T=μ(1)準確度kTUSL Tk --=μ，或LSLT T k --=μ，(k 有時以Ca 符號代替，代表製程準確度)(2)精密度C p 指標C p 指標定義為:σ3T USL C p -=，或σ3LSLT C p -=(3) C pk 指標C pk = C p (1-k ) ，或σμ3-=USL C pk ，σμ3LSLC pk -= 如果如果),(LSL T T ->-μ則C pk =0；如果),(T USL T ->-μ則C pk =0Ｃp 判定表參考例如果是以X -R Chart 之資料來進行製程能力分析，則製程之標準差σ可由2d R 來估計。

制程能力分析

P 1 = P (Y1 < 0) = P ( Z <
0 − 0 .6 ) = P( Z < −1.33) = 0.0918 = 9.18% 0.45
第7章
製程能力分析
77
X 1 > X 2 + 0.5 發生搖晃不率
Y2 = X 1 − X 2 > 0.5 P2 = P (Y2 > 0.5) = P( Z >
0 .5 − 0 .6 ) = P( Z > −0.22) = P ( Z < 0.22) = 0.5871 = 58.71% 0.45
22. P 1+P 2 = 9.18% + 58.71% = 67.89%
能力比 =
1 1 = =1 .199 C p 0.834
15. 可歸為下列三項原因：製程平均有製製的製製；製程變異製自；製程平均有製製製製且製程變異製自。
76
品質管理教師手冊
ˆ = 16. C p
LSL − X ˆ 3σ
=
3.5 − 3.2 = 0.67 3(0.15)
C p 值為 0.67，故 C p 值的自級判定介於 D 自級與 E 自級之間。 USL − X 3σ X − LSL 6 − 5 .8 3 × 0.2 5.8 − 5
C pk = (1 − C a ) × C p = (1 − 0.047)0.834 = 0.795
13. Ca 值為－ 0.047，故 Ca 值的自級判定為 A 自級。 C p 值為 0.834，故 C p 值的自級判定為 D 自級。 C pk 值為 0.795，故 C pk 值的自級判定為 D 自級。 14 .能力比為 C p 值的倒數。 C P 值為 0.834，故其能力比可計算如下：

制程能力分析 (Cpk , Z值)

短期： (1)Z值 = (Xbar-LSL) /σ = (599.938-595)/1.64804 = 2.996 p(2.996)= 0.998632 缺點=1-0.998632=0.001368 =1368 ppm (2)Z值 = (USL-Xbar) /σ = (605-599.938)/1.64804 = 3.0715 p(3.0715)= 0.998935 缺點=1-0.998935=0.001065 =1065 ppm (3)缺點總數 =1367+1064=2421 ppm
Ca、Cp、Cpk Pp、Ppk Z值 (Sigma Level)
計數型數值 (Attribute data)
Defect、DPU DPO、DPMO
2 Cp , 製程精密度 -1
1-製程精密度(Capability of Precision)衡量製程分散寬度符合規格的程度 2-Cp只考慮標準差, 不考慮平均值 3-Cp值愈高, 表示製程能力佳 A 規格寬度 USL – LSL VOC Cp = -------- = ------------------------- = ------------------- = ---------B 實際分散寬度 6σ VOP ◎Cp 等級評定基準： A： Cp ≧ 2.00 B： 2.00 ＞ Cp ≧ 1.33 C： 1.33 ＞ Cp ≧ 1.00 D： 1.00 ＞ Cp
規格寬度=6
距離下限=2.25
距離上限=3.75
平均值偏移=0.75
Target=100 LSL=97
μ = 99.25
USL=103
σ = 0.5
5 Z值, Sigma Level -1
僅有規格上限
USL LSL

制程能力(Cpk)分析教程讲解

A0
日期 07/10/11 页号
页版本 A0
小页号
(二) 正态分布的解释与应用
正态分布函数中的 μ与σ是互相独立的两个分布函数,μ 决定正态曲线的位置,σ决定它的形状.
σ
μ
文件名称章节 5.0
工程能力分析与控制
工序能力分析
第五章:工序能力分析
(一) 工序能力
工序能力是指工序处于稳定状态下的实际加工能力.有时也称工序能力为工序能够稳定的生产出合格品的能力. 从定量的角度看,工序能力是工序本身所固有的一种可以度量的特性.如果工序能力高, 所加工产品质量指针的波动就小,说明工序质量好.
1.可以反映产品质量的波动性(变异形)
从统计学的角度,可以把产品质量波动分为两类:
(1)正常波动: 由随机因素引起的,表明生产过程稳
(2)异常波动: 由系统因素引起的,表明生产过程稳异常;
2.可以掌握产品质量波动的统计规律
在正常的生产的情况下,通过大量的调查., 收集生产现场的产品质量数据,并利用概率论和数统计方法对这些质量数据进行分析与处理,发现和掌握产品质量波动的统计规律,如果其分布情况与正常状态的质量分布不同, 就说明生产过程有异常波动, 如果相同,说明生产过程的波动是正常波动.
(一) 加工精度
在生产制造过程中, 通常采用加工精度这个概念来反映质量的波动程度. 误差大则精度低,误差小则精度高.
精度可分为:
工程能力分析与控制

制程能力分析

A C
1-35
P D
Example 13
1. 鋼板厚度的規格為 ±0.3cm。依隨機抽查鋼板厚度的規格為3±0.3cm。 10件得如下資料，請計算C 10件，得如下資料，請計算 pk, Ca與Cp估計值。計值。
A C
1-36
P D
Example 14
1. 已知u=3.2，σ=0.02。若USL=3.3, =3.2，。 LSL=3.0的情況下，請計算 pk值。的情況下，的情況下請計算C
1. Ca值只考慮製程平均是否偏離規格中而未考慮製程的變異，因此，心，而未考慮製程的變異，因此，不論製程的變異大小為何，論製程的變異大小為何，在相同的製程平均之下，值是一樣的。程平均之下，其Ca值是一樣的。職是之故，之故，單純的用Ca值來衡量製程能力是有偏頗的。力是有偏頗的。
1. 或
USL − LSL ɵ Cp = ɵ 6σ
(雙邊規格)
2. 其中， Cp 為 C p 估計值其中， ˆ 3. Cp值越大，表示製程能力越好。值越大，表示製程能力越好。值越大
A C
1-22
P D
Cp值的意義
1. Cp值必為正值值必為正值(>0)。。 2. Cp值愈大，表示產品品質變異愈小，值愈大，表示產品品質變異愈小，製程精密度愈高。製程能力佳。製程精密度愈高。製程能力佳。 3. Cp值愈小，表示產品品質變異愈大，值愈小，表示產品品質變異愈大，製程精密度愈低。製程能力差。製程精密度愈低。製程能力差。 4. Cp值反應製程潛在的值反應製程潛在的潛在的(potential)製程製程能力。能力。
A C
1-17
P D
Example 4

制程能力分析

C pm 指標
19 製程能力分析 (Process Capability Analysis)
C pm 指標之定義
20 製程能力分析 (Process Capability Analysis)
製程能力之評價
21 製程能力分析 (Process Capability Analysis)
製程能力指標 Ca 的衡量標準
製程能力分析 (Process Capability Analysis)
精確
低
製程能力指標 Cpk
Cpk可分為Ca（精準度）與Cp（精確度）
準確度(Capability of Accuracy)
Ca minUSL T , T LSL
精確度(Capability of Precision)
– – – – –
2 製程能力分析 (Process Capability Analysis)
在競爭廠商之中作一選擇降低製程的變異預測製程是否符合公差協助產品設計人員選擇或是更改製程設立新生產設備之規格
製程能力與公差
一般而言，配合管制圖的使用，而以6s的寬度來表示其生產的製程能力製程能力6s與公差（ＵＳＬ－ＬＳＬ）之間有三種關係
C pk
Min USL x , x LSL 3
CP與CPK 的關係
16 製程能力分析 (Process Capability Analysis)
Example
17 製程能力分析 (Process Capability Analysis)
Example
18 製程能力分析 (Process Capability Analysis)
• 在利用製程能力指標估計不合格率時，假設數據符合常態分配之要求，但如果數據不符合常態分配，則估計之不合格率將不可信

制程能力分析

故製程能力可以產量、效率表示，也可以成品、半成品、零件等之品質特性來表示，也可以不良率或缺點數來表示。

製程能力可為一部機器或一設備在一定條件下操作的能力，前者一般稱為「機器能力」，可為一項預定的產品之全部製程，包括人、材料機器及方法在長時間內所程現的能力。

前者一般稱為「機器能力」，而後者則稱為「綜合製造能力」，後者經常包括了工具損耗之正長影響，材料的微些變化及其它的微小變化。

在此我們所討論之製程能力即以後者為主。

製程能力與規格當考量製程績效之前，必須先討論兩個重要的問題：1.製程是否有維持良好”統計管制狀態”的能力。

2.是否具有產出符合工程規格零件的製程能力。

只有當製程處於”統計管制狀態”下，估計製程能力才合理，因為當製程處於”統計管制狀態”下，製程沒有可歸咎的非自然因素存在，此時才可以顯示製程真正的變異。

此部份已於管制圖介紹中詳細介紹過。

製程是否具有產出符合工程規格零件的能力，在於製程變異範圍是否介於工程規格之內，一邊而言可能有下列三種情況：1.製程變異小於規格間差異。

2.製程變異等於規格間差異。

3.製程變異大於規格間差異。

第一種情況：6＜USL－LSL當製程變異(6)小於規格間之差(USL－LSL)時，這是最理想情況，如圖個別值分布A和規格的關係最佳，因為規格比製程變異大很多，即使製程帄均值有很大的移動，也不易超出規格界線；分佈B的變異比分佈A大，但所有個別值仍在規格之內分佈C所顯示的變異更大，但仍在規格之內。

此種情形具有經濟上的利益，因為即使超出管制界線，如分佈B和C，也布置產生不良品，所以不必時常調整機器或尋找非自然因素。

第二種情況：6＝USL－LSL如圖，製程變異或製程能力等於規格間的差。

如果製程的次數分佈與A相同則有99.74%的產品符合規格；但是當製程帄均移動時(如分佈B)或變異增大時(如分佈C)，則不良率可能遠大於0.06%。

制程能力分析方法介绍共22页文档

合集下载

制程能力分析

制程能力分析

制程能力(Cpk)分析教程.

制程能力分析

制程能力分析(SPC)

制程能力解析

制程能力分析

制程能力分析

制程能力分析 (Cpk , Z值)

制程能力(Cpk)分析教程讲解

制程能力分析

制程能力分析

制程能力分析

文档推荐

最新文档

制程能力分析方法介绍共22页文档

合集下载

制程能力分析

制程能力分析

制程能力(Cpk)分析教程.

制程能力分析

制程能力分析(SPC)

制程能力解析

制程能力分析

制程能力分析

制程能力分析 (Cpk , Z值)

制程能力(Cpk)分析教程 讲解

制程能力分析

制程能力分析

制程能力分析

文档推荐

最新文档

制程能力(Cpk)分析教程讲解