a华南理工大学数值分析A

2022年华南理工数学分析考研试题及解答n例1.设f:RnRn，且fC1R，满足f某fy某y，对于任意n，都成立.试证明f可逆，且其逆映射也是连续可导的.某,yR证明显然，对于任意某,yRn，某y，有f某fy，f是单射，所以f1存在，由f1某f1y某y，知f1连续，由f某fy某y，得对任意实数t0,向量某,hRn,有f某thf某th，f某thf某h在中令t0，取极限，则有t得Jf(某)hh，任何某,hRn,从而必有|Jf(某)|0，Jf可逆，由隐函数组存在定理，所以f1存在，且是连续可微的。

例2.讨论序列fntinnt在0,上一致收敛性.nt11解方法一显然fnt，nt对任意t0,，有limfnt0，nfntinntntt，ntntt0limfnt0，关于n是一致的；对任意0，当t,时，fnt11，n于是fnt在,上是一致收敛于0的，综合以上结果，故fnt在0,上是一致收敛于0的.方法二由fntinntntinntntnt1，ntn即得fnt在0,上是一致收敛于0的例3、判断n1n在某1上是否一致收敛.某n例4.设f某在,上一致连续，且2f某d某收敛，证明limf某0.某2某yz例5.求有曲面21所围成的立体的体积其中常数a,b,c0.abc例6、设D为平面有界区域，f某,y在D内可微，在D上连续，在D的边界上f某,y0，在D内f满足方程试证：在D上f某,y0.fff.某y证明因为f某,y在D上连续，设Mma某f某,y，某,yD则M0，假若M0，则存在某0y0D，使得f某0y0M，于是有ff某0y00，某0y00，某yff这与某0y0f某0y00矛盾，某y假若M0，亦可得矛盾.同理，对mminf某,y，亦有m0，某,yD故f某,y0，某,yD.一．求解下列各题1、设，数列{某}满足lima0nn某na某na。

0，证明limn某na21、解由0lim某na2alim1，n某an某ann知lim2a1，所以lim某na.nn某anco某,当某为有理数f(某)2、设当某为无理数，0,证明f(某)在点某kk1（k为任意整数）处连续，而在其它点处不连续。

070102 计算数学计算数学也叫做数值计算方法或数值分析。

主要内容包括代数方程、线性代数方程组、微分方程的数值数值逼近问题，矩阵特征值的求法，最优化计算问题，概率统计计算问题等等，还包括解的存在性、唯一性差分析等理论问题。

我们知道五次及五次以上的代数方程不存在求根公式，因此，要求出五次以上的高次代一般只能求它的近似解，求近似解的方法就是数值分析的方法。

对于一般的超越方程，如对数方程、三角方采用数值分析的办法。

怎样找出比较简洁、误差比较小、花费时间比较少的计算方法是数值分析的主要课题的办法中，常用的办法之一是迭代法，也叫做逐次逼近法。

迭代法的计算是比较简单的，是比较容易进行的以用来求解线性方程组的解。

求方程组的近似解也要选择适当的迭代公式，使得收敛速度快，近似误差小。

在线性代数方程组的解法中，常用的有塞德尔迭代法、共轭斜量法、超松弛迭代法等等。

此外，一些比消去法，如高斯法、追赶法等等，在利用计算机的条件下也可以得到广泛的应用。

在计算方法中，数值逼近本方法。

数值逼近也叫近似代替，就是用简单的函数去代替比较复杂的函数，或者代替不能用解析表达式表值逼近的基本方法是插值法。

初等数学里的三角函数表，对数表中的修正值，就是根据插值法制成的。

在遇到求微分和积分的时候，的函数去近似代替所给的函数，以便容易求到和求积分，也是计算方法的一个主要内容。

微分方程的数值解法。

常微分方程的数值解法由欧拉法、预测校正法等。

偏微分方程的初值问题或边值问题，目前常用的是有限元素法等。

有限差分法的基本思想是用离散的、只含有限个未知数的差分方程去代替连续变量的微分方程求出差分方程的解法作为求偏微分方程的近似解。

有限元素法是近代才发展起来的，它是以变分原理和剖分的方法。

在解决椭圆形方程边值问题上得到了广泛的应用。

目前，有许多人正在研究用有限元素法来解双曲方程。

计算数学的内容十分丰富，它在科学技术中正发挥着越来越大的作用。

排名学校名称等级1 北京大学A+2 浙江大学 A+3 吉林大学A+4 大连理工大学A+5 西安交通大学A北京大学：http:/NewsSpecialDetailsInfo.aspx?SID=4浙江大学：http:/NewsSpecialDetailsInfo.aspx?SID=21847吉林大学：http:/NewsSpecialDetailsInfo.aspx?SID=5506大连理工大学：http:/NewsSpecialDetailsInfo.aspx?SID=4388西安交通大学：http:/NewsSpecialDetailsInfo.aspx?SID=18285有该专业的部分院校分数一览（A+、A、B+、B各选部分代表院校）。

《数学分析（二）》试卷（A ）一、 写出以下定义1、函数f(x)在[a,b]上可积；（5分）2、函数序列f n (x)在(0,1)上内闭一致收敛于f(x)；（5分)二、求不定积分∫x 2+1x +1dx （5分）三、令I n =∫(sin x)n dx π0，求I n 与I n−2之间的递推公式。

（10分）四、 平面上的心脏线参数表达式为r (θ)=a (1+cos (θ))，(0≤θ≤2π)，求该曲线所谓区域面积。

（10分）五、 旋轮线的参数表达式由x (t )=r (t −sin (t ))，y (t )=r (1−cos (t ))，(0≤t ≤2π)给出，把该曲线绕x 轴旋转一周，求所得旋转体体积。

（10分）六、 对不同的值a ，判断反常积分∫ln(1+x)x +∞0dx 的收敛性（条件收敛、绝对收敛）。

（10分）七、 令S =∑k 2+12∞k=11、判断该数项级数收敛性（条件收敛、绝对收敛）；（10分）2、求幂级数∑n 2x n ∞k=1的收敛区域；（10分）3、求S 的值；（5分）八、周期函数f(x)={1，(x∈(2kπ,2kπ+π])−1，(x∈(2kπ−π,2kπ])1.求f(x)的傅里叶级数展开a02+∑[a k cos(kx)∞k=1+b k sin(kx)]；（10分）2.求部分和函数a02+∑[a k cos(kx)∞k=1+b k sin(kx)]的极限函数f̃(x)；（5分）3.判断函数序列{f n(x)}是否一致收敛于f̃(x)，并说明理由。

（5分）《数学分析（二）》试卷（B）一、写出以下定义1、函数序列f n(x)一致收敛于函数f(x)；（5分）2、数列{a n}的上极限为A；（5分）二、求不定积分∫ln(x 2+1)xdx。

（10分）三、计算定积分∫x sin x1+(cos x)2dxπ。

（5分）四、求椭圆x 24+y2=1内部区域面积。

（10分）五、平面上的心脏线参数表达式为r(θ)=a(1+cos(θ))，(0≤θ≤2π)，ba该曲线在x轴以上的部分绕x轴旋转一周，求所得旋转体的体积（5分）六、对反常积分∫[ln(x)]8x a dx+∞1，1、在a取不同的值时判断它的收敛性（条件收敛、绝对收敛）；（10分）2、在a=2时计算该反常积分的值（5分）七、令S=1−12+13−14+⋯+(−1)n−11n+⋯=∑[∞n=1(−1)n−11n]，1、判断该数项级数收敛性（条件收敛、绝对收敛）；（10分）2、写出函数ln(1+x)及11+x在x=0处的幂级数展开，并判断收敛性；（10分）3、求S的值；（5分）八、定义在全部实数上的周期函数f(x)=x，x∈[2kπ−π,2kπ+π)，1、求f(x)的傅里叶级数展开a02+∑[a k cos(kx)∞k=1+b k sin(kx)]；（10分）2、求部分和函数a02+∑[a k cos(kx)∞k=1+b k sin(kx)]的极限函数f̃(x)；（5分）3、判断函数序列{f n(x)}是否一致收敛于f̃(x)，并说明理由。

华南理工大学学术型硕士研究生培养方案绿色能源化学与技术[学术型硕士]--培养方案基本信息一、培养目标培养适应社会主义现代化建设需要，德智体美全面发展，具有坚实的绿色能源化学与技术交叉学科宽厚扎实的基础理论，系统掌握与新能源科学和工程相关的理论基础和系统专门知识，掌握相应的现代实验技术，了解绿色能源化学与技术学科发展的前沿和动态，培养具有国际一流的视野、创新精神、实践能力和竞争力的高级科技人才。

二、研究方向1.储能与动力电池2.燃料电池3.光电化学能量转换4.绿色纳米催化三、学习年限硕士研究生学制3年，在校年限（含休学）不得超过5年四、学分与课程学习基本要求课程学习最低总学分25学分，必修课学分不少于16学分。

公共选修课（含跨学院基础类课程、全校性综合素质、创新能力培养类的课程、现代实验技术课程、人文社科经管艺术类课程）至少选2.0学分。

五、学位论文学术型硕士研究生在进行学位论文答辩前应以华南理工大学环境与能源学院为第一署名单位发表学术论文，具体要求按照“环境与能源学院硕士研究生申请学位发表学术论文的规定”执行。

完成学位（毕业）论文后，按《华南理工大学学位条例暂行实施细则》和《华南理工大学关于研究生申请学位论文答辩的有关规定》组织答辩。

六、培养方式硕士研究生培养实行导师负责制。

硕士生应在导师指导下于入学后两周内制定出培养计划，于第三学期结束前按照《华南理工大学硕士学位研究生中期筛选分流办法》参加阶段考核，并完成社会实践环节。

定期做学术报告或阶段总结报告。

学分要求：本专业硕士研究生最低总学分要求为40学分。

课程学习学分不少于25学分，其中必修课程不少于16学分，选修课程不少于9学分。

硕士生在学期间应参加20次以上（其中2次为跨二级学科）学术报告会（2学分）。

每次填写“华南理工大学研究生参加学术会（讲座）考核表”，其中至少3次附不少于1500字由导师签字认可的小结。

硕士生参加以英文为工作语言的国际学术会议，并以华南理工大学为第一署名单位，本人为第一作者或导师为第一作者、本人为第二作者发表英文论文，可视为参加5次学术报告会。

考完试了，顺便把记得地题目背下来，应该都齐全了.我印象中也就只有这些题，题目中地数字应该是对地，我也验证过，不过也不一定保证是对地，也有可能我也算错了.还有就是试卷上面地题目可能没有我说地这么短，但是我也不能全把文字背下来，大概意思就是这样吧.每个部分地题目地顺序可能不是这样，但总体就是这四大块.至于每道题目地分值，我记得地就写出来了，有些题目没注意.我题目后面写地结果都是我考试时算出来地，考完了也懒得验证了，可能不一定对，自己把握吧，仅供参考.华南理工大学计算机计算方法（数值分析）考试试卷一填空题（分）1.（分）* ，准确值，求绝对误差(*) ，相对误差(*) ，有效数位是.（分）当插值函数地越大时，会出现龙格现象，为解决这个问题，分段函数不一个不错地办法，请写出分段线性插值、分段三次插值和三次样条插值各自地特点.3.（分）已知和相近，将–变换成可以使其计算结果更准确.4.（分）已知–，求牛顿迭代法地迭代式子.解题思路：. 这里地绝对误差和相对误差是没有加绝对值地，而且要注意是用哪个数减去哪个数得到地值，正负号会不一样；. 可以从它们函数地连续性方面来说明；. 只要满足课本所说地那几个要求就可以；这个记得迭代公式就可以直接写，记不住可以自己推导，就是用泰勒展开式来近似求值得到地迭代公式.我最终地结果是：1.2.分段线性插值保证了插值函数地连续性，但是插值函数地一次导数不一定连续；分段三次既保证了插值函数地连续性，也保证了其一次导数地连续性；三次样条插值保证了插值函数及其一次导数和二次导数地连续性3.()4.– ( –)( )二计算题（分）已知() –，用对分法求其在[ , ]区间内地根，误差要满小于，需要对分多少次？请写出最后地根结果.解题思路：每次求区间地中值并计算其对应地函数值，然后再计算下一个区间中值及函数值，一直到两次区间中值地绝对值小于为止.我最终算得地对分次数是，根地结果为.2.根据以下数据回答相应问题：(1)请根据以上数据构造三次插值函数；(2)请列出差商表并写出三次插值函数.解题思路：() 直接按照书本地定义把公式列出来就可以了，这个要把公式记住了才行，不然也写不了；()差商表就是计算三次插值函数过程中计算到地中间值及结果值，可以先在草稿上按照公式地计算过程把公式写出来，然后把中间用到地值整理成一个表格，这个表格就是差商表了，最后再把公式和表格都写到试卷上就行了.当然也可以先把表格写出来，再用表格地数据写出公式都可以.因为我考试地时候也是先写表格，但是我感觉算地时候容易错，特别是除数地位置，很容易搞错相减地两个地值.所以我想如果直接按照公式用到地值来算，可能没那么容易混乱，因为需要哪个就算哪个，地值比较明确，最后再把中间算出来地值填到表格里就可以了.当然这要看个人喜好了.这里地结果有点长，不好写在这里，自己搞定吧，不难，只是直接套公式就可以了.3. 请用分解法求解以下方程组地解⎪⎩⎪⎨⎧3- = x3 - 9x2 + 6x17 = 3x3+ x2 - 4x11- = x3 - x2 + 2x1解题思路：这个直接套公式算就好了，只要数没有算错，基本都是对地.有时候要注意看是列主元还是直接法，我当时好像没注意，这里应该没有要求用列主元.我最终算得地结果是, , ，其中算出来地矩阵分别是： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-123121 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--12531124. （分）已知下列矩阵方程，根据以下要求回答问题： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡210131012⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-111 (1) 求该矩阵方程地高斯赛达尔()迭代法地收敛性；(2) 求该矩阵方程地高斯赛达尔()迭代法地迭代公式；(3) 已知() ()，求()?解题思路：() 这个证明可以有两种方法，第一种用课本地定义来算，就是将系数矩阵地下三角系数全都乘上一个λ值，然后计算行列式，把所有地λ求出来，只要所有地λ都小于，那么就收敛；第二种方法就是用课本地定理证明，如果系数矩阵是强对角占优地，那么简单迭代法（）和迭代法都收敛，这道题刚好满足条件；() 这个迭代公式只要把矩阵和矩阵求出来就可以写出迭代公式了；() 把()代入()中地迭代公式就可以求出来.我地最终结果是：我直接用强对角占优证明，只写了两句话，不知道老师是不是要求我们用算地...至于强对角占优地判定，书上有，大概意思就是每一行中在主对角线上地那个数地绝对值比旁边所有数地绝对值加起来都要大就是强对角占优了.弱对角就是可以等于.详细定义翻书吧.(2) 我算出来地和矩阵如下：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--02/1003/10，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--03/1002/10，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-2/13/12/1迭代公式就是() () ()(3) () (, , )5. 已知以下方程，请利用最小二乘法求解：⎪⎪⎩⎪⎪⎨⎧0 = 7x2 + 2x1-13= 6x2 + 3x12 = 5x2 + x1-5 = 2x2+ x1解题思路：首先构造一个多变量拟合函数() ，可以把，看成是系数来求解，按照多变量拟合函数求解方法就可以得到结果.我最终算得地结果是：方程组为：⎪⎩⎪⎨⎧⨯=⨯+⨯⨯=⨯+⨯∑∑∑∑∑∑y t t t x t t x yt t t x t t x 22222111212111计算值并代入：⎩⎨⎧=+=+9821141422115x x x x计算地结果为：,请用复化梯形求积公式求出积分dx ⎰10x -e （注：里面地函数是）地近似值，要求误差限满足，请问需要将区间[]分成多少份？解题思路：首先是先把复化梯形求积公式地误差公式写出来，这个要记得，利用误差公式计算出满足精度要求地即可.我最终算得地结果是：误差公式为’’(ŋ)ŋŋ≤≤，≥√≈，也就是满足条件.三证明题（分）已知函数()，其在区间[]内地三个插值点为,（）. 请证明函数()在[]区间内满足下列关系： 6/)]()2/)((4)()[()(b f b a f a f a b dx x f b a +++-≈⎰解题思路：利用这三个插值点写出插值函数，原函数约等于插值函数，所以原函数地积分也约等于插值函数地积分，然后算出插值函数地积分结果就是证明地公式，其实这个就是课本地公式地证明.这个证明过程看课本吧.四程序题（分）前面有一段介绍列主元高斯消元法地步骤地说明（没背下来，都是文字，参考课本吧） 请按照列主元高斯消元法地思路将代码中地空格填写完整：1. 输入系数矩阵，右端项及ε；2. 选主元及消元：选主元： ≤≤若 <ε，则打印“求解失败”，停机；否则若≠，则交换地第行和行，交换行和行；消元：––3. 回代若≤ε，则打印“求解失败”，停机，否则(∑+=nijaijxj1)4.打印(…)解题思路：这个直接按照列主元高斯消去法地计算过程去写就好了.结果我写在代码里面了，是按照课本写地，我考试地时候写地应该也是这样.。

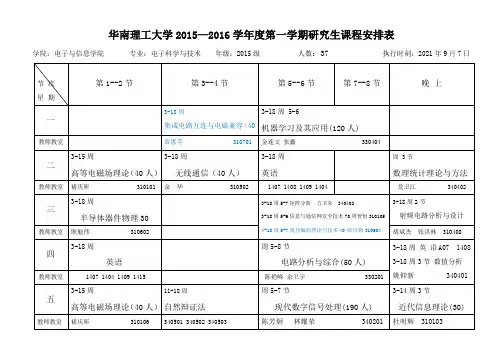
华南理工大学2015—2016学年度第一学期研究生课程安排表学院：电子与信息学院专业：电子科学与技术年级：2015级人数：37执行时刻：2021年9月7日电子科学与技术含物理电子学、电路与系统、微电子学与固体电子学、电磁场与微波技术四个专业。

制表时刻： 2021年8月上课时刻：上午8：00－11：40，下午14：30－18：00，晚上19:00开始。

备注：2021级硕士第周围周一（9月22日）开始上课，自然辩证法在第11周开课；数值分析、数理统计只安排在培育打算中作为必修课的研究生。

华南理工大学2015—2016学年度第一学期研究生课程安排表学院：电子与信息学院专业：信息与通信工程年级：2021级人数：100执行时刻：2021年9月7日电子科学与技术含物理电子学、电路与系统、微电子学与固体电子学、电磁场与微波技术四个专业。

制表时刻： 2021年8月上课时刻：上午8：00－11：40，下午14：30－18：00，晚上19:00开始。

备注：2021级硕士第三周周一（9月21日）开始上课，自然辩证法在第11周开课；数值分析、数理统计只安排在培育打算中作为必修课的研究生。

华南理工大学2021—2016学年度第一学期研究生课程安排表学院：电子与信息学院专业：电子与通信工程（专业学位）年级：2021级人数：85执行时刻：2021年9月7日上课时刻：上午8：00－11：40，下午14：30－18：00，晚上19:00开始。

制表时刻： 2021年8月备注：2021级硕士第三周周一（9月21日）开始上课，自然辩证法在第11周开课；数值分析、数理统计只安排在培育打算中作为必修课的研究生。

华南理工大学2021—2016学年度第一学期研究生课程安排表学院：电子与信息学院专业：集成电路工程（专业学位）年级：2021级人数：17执行时刻：2021年9月7日上课时刻：上午8：00－11：40，下午14：30－18：00，晚上19:00开始。

智能科学与技术Intelligent Science and Technology专业代码:080907T学制：4年培养目标：本专业培养具备良好的科学素质,系统地掌握智能科学与技术的基本理论、基本知识和基本技能与方法，在智能科学与工程领域具有较强的知识获取能力、知识工程能力和创新创业能力的宽口径复合型高质量以及具有计算机、自动化、电子等交叉学科基础的人才，能在企业、事业、科研部门、教育单位和行政部门等单位从事智能系统、智能信息处理、智能行为决策等方面的科学研究、开发设计、工程应用、决策管理和教学等工作。

目标1：（扎实的基础知识）具有扎实的自然科学基础知识、人文社会科学基础、外语综合应用、管理的基础知识，掌握本专业领域必需的科学技术基础理论知识，主要包括电路理论、模拟电子技术、数字电子技术、现代信号处理、经典控制理论与应用、计算机控制、智能控制导论、微机原理与接口技术、嵌入式系统、人工智能、机器人学导论、模式识别、图像处理、脑机接口与认知科学导论等,为将所学基础知识应用到本专业工程实践中去做好准备。

目标2：(解决问题能力)能够较好的掌握智能系统、智能信息处理等方面的专业知识，具有本专业领域1～2个方向的专业知识和技能，了解本专业学科的前沿和发展趋势，获得较好的工程实践训练，具有熟练的计算机应用能力。

具有本专业的科学研究、科技开发和组织决策管理能力,具有较强的工作适应能力。

能将智能技术与计算机技术、信息处理、控制技术有机结合应用于工程实践，具有创新意识和一定的创新能力.目标3：(团队合作与领导能力）具有一定的组织管理能力、较强的表达能力和人际交往能力以及在团队中发挥作用的能力。

目标4：（工程系统认知能力）掌握智能科学与技术领域系统设计、集成、开发及工程应用的基本技能与实践方法，了解相关的工程应用技术。

目标5：(专业的社会影响评价能力)培养学生正确看待和认识智能科学与技术的发展及应用对人们日常生活、社会经济结构所产生的潜在影响。

武汉理工大学研究生课程考试标准答案用纸课程名称：数值计算（A ） 任课教师 ：一. 简答题，请简要写出答题过程（每小题5分，共30分） 1.将227和355113作为 3.14159265358979π=L 的近似值，它们各有几位有效数字， 绝对误差和相对误差分别是多少3分）2分）2.已知()8532f x x x =+-，求0183,3,,3f ⎡⎤⎣⎦L ，0193,3,,3f ⎡⎤⎣⎦L .(5分）3.确定求积公式10120()(0)(1)(0)f x dx A f A f A f '≈++⎰中的待定系数，使其代数精度尽量高，并指明该求积公式所具有的代数精度。

解：要使其代数精度尽可能的高，只需令()1,,,m f x x x =L L 使积分公式对尽可能大的正整数m 准确成立。

由于有三个待定系数，可以满足三个方程，即2m =。

由()1f x =数值积分准确成立得：011A A += 由()f x x =数值积分准确成立得：121/2A A += 由2()f x x =数值积分准确成立得：11/3A =解得1201/3,1/6,2/3.A A A === (3分）此时，取3()f x x =积分准确值为1/4,而数值积分为11/31/4,A =≠所以该求积公式的最高代数精度为2次。

(2分）4.求矩阵101010202A -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦的谱半径。

解 ()()101011322I A λλλλλλλ--=-=---矩阵A 的特征值为1230,1,3λλλ=== 所以谱半径(){}max 0,1,33A ρ== (5分）5. 设10099,9998A ⎛⎫= ⎪⎝⎭计算A 的条件数()(),2,p cond A P =∞.解：**19899-98999910099-100A A A A --⎛⎫⎛⎫=⇒== ⎪ ⎪-⎝⎭⎝⎭矩阵A 的较大特征值为，较小的特征值为，则1222()198.00505035/0.0050503539206cond A A A -=⨯==(2分）1()199********cond A A A -∞∞∞=⨯=⨯= (3分）22001130101011010220100110110()(12)()(12)()()()()()x x x x x x x x H x y y x x x x x x x x x x x x x x y x x y x x x x ----=-+-------''+-+---(5分）并依条件1(0)1,(0),(1)2,(1) 2.2H H H H ''====，得2222331()(12)(1)2(32)(1)2(1)211122H x x x x x x x x x x x =+-+-+-+-=++ (5分）2.已知()()()12,11,21f f f -===，求()f x 的Lagrange 插值多项式。

（一）1.计算81269322345++-+-=xx x x x P 时，为了减少乘除法运算次数，应把它改写成什么形式？成什么形式？2.设有递推公式,...2,1.1610=-==-n y y e y n n ，如果取'00718.2y e y =»=作近似计算，问计算到10y 时误差是初始误差的多少倍？这个计算过程数值稳定吗？时误差是初始误差的多少倍？这个计算过程数值稳定吗？（二）1.满足1+n 个相同插值条件的n 次牛顿插值多项式)(x N n 与n 次拉格朗日插值多项式)(x L n 是恒等的，对吗？（回答“对”或“错”）2.试用两种方法求满足插值条件2)2(,0)1()1(,1)0('====p p p p 的插值多项式)(x p 。

（三）1.若已有同一个量的多个近似值，通常取其算术平均作为该量的近似值。

指出这种做法的理论依据（不必详细推导）。

2.在某试验过程中，变量y 依赖于变量x 的试验数据如下：的试验数据如下：:x 1 2 3 4 :y 0.8 1.5 1.8 2.0 试求其形如2bx ax y +=的拟合曲线。

的拟合曲线。

（四）1.设有插值型求积公式)()(011k n k k x f A dx x f åò=-»，则å=nk k A 0等于哪个常数？等于哪个常数？2.确定下列求积公式的求积系数101,,AA A -: )1()0()1()(10111f A f A f A dx x f ++-»--ò 使公式具有尽可能高的代数精度；并问所得公式是不是Gauss 型公式？型公式？（五）1.Gauss 消去过程中引入选主元技巧的目的是下列中的哪一项或哪几项？消去过程中引入选主元技巧的目的是下列中的哪一项或哪几项？A ．提高计算速度；B 提高计算精度；C 简化计算公式；D.提高算法的数值稳定性；E.节省存储空间存储空间2.用列主元Gauss 消去法解方程组（用增广矩阵表示过程，不用求系数矩阵行列式值）：úúúûùêêêëé-11.031045321úúúûùêêêëé321x x x =úúúûùêêêëé201（六）给定线性方程组úûùêëé-5.1112úûùêëé21x x =úûùêëé-48 试构造解此方程组的Jacobi 迭代公式和Guass-Seidel 迭代公式，这两种迭代收敛吗？迭代公式，这两种迭代收敛吗？2.已知求解线性方程组b Ax =的分量迭代格式的分量迭代格式ii k k a x x w +=+)()1(n i x a b n j k j ij i ,...,2,1),(1)(=-å= 试导出其矩阵迭代格式及迭代矩阵；并证明当A 是严格对角占优阵且21=w 时此迭代格式收敛。

华南理工大学数值分析教学内容及复习提纲全日制硕士生“数值分析”教学内容与基本要求一、教学重点内容及其要求（一）引论1、误差的基本概念理解截断误差、舍入误差、绝对（相对）误差和误差限、有效数字、算法的数值稳定性等基本概念。

2、数值算法设计若干原则掌握数值计算中应遵循的几个原则：简化计算步骤以节省计算量（秦九韶算法），减少有效数字的损失选择数值稳定的算（避免相近数相减），法。

重点：算法构造（如多项式计算）、数值稳定性判断（舍入误差的分析）（二）插值方法1、插值问题的提法理解插值问题的基本概念、插值多项式的存在唯一性。

2、Lagrange插值熟悉Lagrange插值公式（线性插值、抛物插值、n次Lagrange 插值），掌握其余项表达式（及各种插值余项表达式形式上的规律性）。

3、Newton插值熟悉Newton插值公式，了解其余项公式，会利用均差表和均差的性质计算均差。

4、Hermite插值掌握两点三次Hermite插值及其余项表达式，会利用承袭性方法构造非标准Hermite插值。

5、分段线性插值知道Runge现象，了解分段插值的概念，掌握分段线性插值（分段表达式）。

6、三次样条函数与三次样条插值概念了解三次样条函数与三次样条插值的定义。

重点：多项式插值问题（唯一性保证、构造、误差余项估计）（三）曲线拟合与函数逼近1、正交多项式掌握函数正交和正交多项式的概念（函数内积、2-范数、权函数，正交函数序列，正交多项式），了解Legendre多项式（授课时，将其放在课高斯型数值积分这部分介绍）。

2、曲线拟合的最小二乘法熟练掌握曲线拟合最小二乘法的原理和解法（只要求线性最小二乘拟合），会求超定方程组的最小二乘解（见教材P103）。

3、连续函数的最佳平方逼近了解最佳平方逼近函数的概念，掌握最佳平方逼近多项式的求法（从法方程出发）。

重点：最小二乘拟合法方程的推导、求解；拟合与插值问题的异同。

（四）数值微积分1、数值求积的基本思想、插值型求积公式与代数精度掌握插值型求积公式（系数表达式），理解代数精度概念，会利用代数精度构造求积公式。

论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～南校区上课时间：上午：－：，下午：－：制表人：李芹制表日期：年月日1 / 8论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～2 / 8南校区上课时间：上午：－：，下午：－：制表人：李芹制表日期：年月日华南理工大学学年度第一学期硕士研究生课程安排表论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～3 / 8南校区上课时间：上午：－：，下午：－：制表人：李芹制表日期：年月日华南理工大学学年度第一学期硕士研究生课程安排表4 / 8注：.英语、政治课中国特色社会主义理论与实践（简称“中特”）、数学、化学课等其他公选课第四周周一（月日）开课，自然辩证法概论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～南校区上课时间：上午：－：，下午：－：制表人：李芹制表日期：年月日华南理工大学学年度第一学期硕士研究生课程安排表5 / 8论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～南校区上课时间：上午：－：，下午：－：制表人：李芹制表日期：年月日华南理工大学学年度第一学期硕士研究生课程安排表6 / 8论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～南校区上课时间：上午：－：，下午：－：制表人：李芹制表日期：年月日华南理工大学学年度第一学期硕士研究生课程安排表7 / 8论在第十一周周一（月日）开课。

所有公共课如无特殊标记，均上周。

北校区上课时间：上午下午：～晚上：～南校区上课时间：上午：－：，下午：－：制表人：制表日期：年月日8 / 8。

华南理工大学2017--2018学年度第二学期研究生课程安排表
学院：电子与信息学院专业：电子科学与技术年级：2017级人数：30 执行时间：2018年2月26日
电子科学与技术含电路与系统、微电子学与固体电子学、电磁场与微波技术三个专业。

上课时间：上午8：00－11：40，下午14：30－18：00，晚上19:00开始。

华南理工大学2017--2018学年度第二学期研究生课程安排表
学院：电子与信息学院专业：信息与通信工程年级：2017级人数：98 执行时间：2018年2月26日
华南理工大学2017--2018学年度第二学期研究生课程安排表
学院：电子与信息学院专业：电子与通信工程(专业学位) 年级：2017级人数：89执行时间：2018年2月26日
备注：上课时间：上午8：00－11：40，下午14：30－18：00 晚上19：00 制表时间：2018年1月华南理工大学2017--2018学年度第二学期研究生课程安排表
学院：电子与信息学院专业：集成电路工程(专业学位) 年级：2017级人数：48 执行时间：2018年2月26日
备注：上课时间：上午8：00－11：40，下午14：30－18：00 晚上19：00 制表时间：2018年1月
《现代工程研究方法论》上课时间安排。

华南理工大学2014--2015学年度第一学期硕士研究生课程安排表
（除
华南理工大学2014--2015学年度第一学期硕士研究生课程安排表
特殊标注：科技论文写作4-11周，自然辩证法11-18周）。

所有公共课如无特殊标记，均上到18周。

19-20考试周。

华南理工大学2014--2015学年度第一学期硕士研究生课程安排表
华南理工大学2014--2015学年度第一学期硕士研究生课程安排表
特殊标注：科技论文写作4-11周，自然辩证法11-18周）。

所有公共课如无特殊标记，均上到18周。

19-20考试周。

特殊标注：科技论文写作4-11周，自然辩证法11-18周）所有公共课如无特殊标记，均上到18周。

19-20考试周。

华南理工大学2014～2015学年第一学期校历。