赤平投影原理与应用简介汇总
- 格式:ppt
- 大小:1.11 MB
- 文档页数:8




赤平投影图原理赤平投影图是一种常用的地图投影方式,广泛应用于地理学、地图制作、导航系统等领域。
它是一种将地球表面的经纬度坐标转换为平面坐标的方法,以便更方便地表示地球表面的地理信息。
赤平投影图的原理基于地球的形状和旋转。
地球是一个近似于椭球体的三维物体,而赤平投影图是将这个三维物体投影到一个平面上。
在赤平投影图中,地球的赤道被映射到平面的中心,而其他纬度线则以放射状的方式向外展开。
具体来说,赤平投影图的原理如下:1. 坐标系统选择:赤平投影图使用的是赤道坐标系统,其中赤道被定义为坐标系的原点。
经度则以赤道上的某个点为基准,通常选择格林尼治子午线作为起点。
2. 投影方式选择:赤平投影图采用的是等面积投影方式,也称为兰勃托投影。
这意味着在投影过程中,保持了地球表面上各个区域的面积比例,避免了地图上的失真。
3. 投影计算:将地球上的经纬度坐标转换为平面坐标的过程中,需要进行一系列的数学计算。
这些计算包括将经纬度转换为弧度、计算投影中心、计算投影坐标等步骤。
4. 坐标转换:经过投影计算后,地球上的每个点都被映射到了平面上的对应位置。
这些平面坐标可以通过数学公式进行转换,以便在地图上准确表示地理信息。
赤平投影图的优点是能够保持地图上各个区域的面积比例,使得地图更加真实和准确。
它广泛应用于导航系统中,帮助人们更好地理解和使用地图。
此外,赤平投影图也被用于地理学研究中,用于表示地球表面的地理现象和分布规律。
然而,赤平投影图也存在一些缺点。
由于地球是一个三维物体,将其投影到平面上必然会引起一定程度的失真。
在赤平投影图中,纬度线越远离赤道,失真程度越大。
这意味着在极地地区,地图上的地理信息可能会有较大的偏差。
为了解决这个问题,人们还发展了其他类型的地图投影方式,如墨卡托投影、极射投影等。
这些投影方式各有优缺点,适用于不同的地理区域和应用领域。
总结起来,赤平投影图是一种常用的地图投影方式,通过将地球表面的经纬度坐标转换为平面坐标,方便地表示地球表面的地理信息。






一、序言岩质边坡稳定性分析方法有许多,但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法,还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》(GB50021-94)推荐法等,在计算边坡稳定性系数时,需要知道滑体控制平面(包括结构面和坡面、坡顶面)或直线(包括平面的法线)的地质产状,以及平面与平面、直线与直线、直线与平面间夹角等。
其中平面和直线的产状可以通过现场测量获取,除此之外的几何参数,在没有发明极射赤平投影之前,都是用计算法求得,不仅它们的计算公式复杂,而且计算过程繁琐,也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数,那就可以简化这些几何参数的计算过程,而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
二、极射赤平投影的基本原理(一)投影要素极射赤平投影(以下简称赤平投影)以圆球作为投影工具,其进行投影的各个组成部分称为投影要素,包括:1.投影球(也称投射球):以任意长为半径的球。
2.球面:投影球的表面称为球面。
3.赤平面(也称赤平投影面):过投影球球心的水平面。
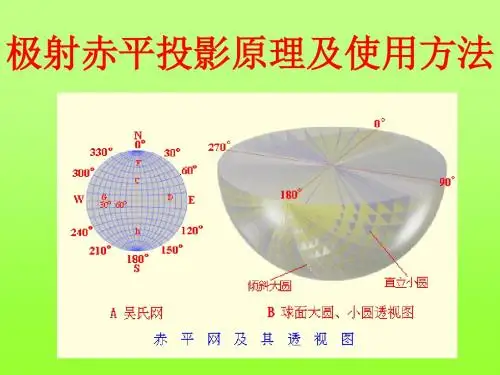
4.大圆:通过球心的平面与球面相交而成的圆,统称为大圆(如图一(a)中ASBN、PSFN、NESW),所有大圆的直径相等,且都等于投影球的直径。
当平面直立时,与球面相交成的大圆称为直立大圆(如图一(a)中PSFN);当平面水平时,与球面相交成的大圆称为赤平大圆或基圆(如图一(a)中NESW);当平面倾斜时,与球面相交成的大圆称为倾斜大圆(如图一(a)中ASBN)。
5.小圆:不过球心的平面与球面相而成的圆,统称为小圆(如图一(b)、(c)中AB、CD、FG、PACB)。
当平面直立时,与球面相交成的小圆称为直立小圆(如图一(b)中DC);当平面水平时,与球面相交成的小圆称为水平小圆(如图一(b)中AB);当平面倾斜时,与球面相交成的小圆称为倾斜小圆(如图一(b)中FG或图一(c)中PACB)。
赤平投影原理与操作方法
赤平投影是一种把三维球体表面映射到二维平面上的技术。
技术原理是从球体中心到表面上各点的线段与平面垂直,投影到平面上得到的投影坐标。
操作方法:
1. 选择一个球体,并确定其中心坐标和半径大小。
2. 确定投影平面,通常为xoy 平面或者xoz 平面,也可以自定义一个平面。
3. 将球体表面上的每个点投影到平面上得到对应的坐标点。
4. 将投影得到的坐标点按照一定的规律映射到二维平面上形成图像,通常会使用等距投影或者等面积投影等方法进行映射。
5. 根据需要作出相应的修改,例如旋转角度、缩放大小等。
赤平投影可以有效地呈现球体表面上的信息,并且具有保持距离和角度比例不变、投影区域面积相等等优点。
常用于地图制作、天文学和计算机图形学等领域。