行线分线段成比例定理
- 格式:pptx
- 大小:88.14 KB
- 文档页数:6

平行线分线段成比例一、知识要点1.平行线分线段成比例定理:三条平行线截两条直线所得对应线段成比例.2.推论:平行于三角形一边的直线截其它两边(或其延长线)所得对应线段的比相等.二、知识要点及典型例题精讲【知识要点1】——平行线分线段成比例定理若1l ∥2l ∥3l ,则;;AB DE AB DE BC EF BC EF AC DF AC DF===. 例1 如图,已知直线a ∥b ∥c ,直线m ,n 与a ,b ,c 分别交于A 、C 、E 、B 、D 、F ,AC=4,CE=6,BD=3,则BF 等于 .【知识要点2】——平行线分线段成比例定理推论如果BC ∥DE ,则AD AE AB AC =;AD AE BD CE =;BD CE AB AC=. 例2 如图,在ABC 中,点D 、E 分别在边AB 、AC 上,DE ∥BC,若AD:AB=3:4 ,AE=6,则AC= .【随堂练习三】一、判断题1.三条平行线截两条直线,所得的线段成比例( )2.一条直线交△ABC 的边AB 于点D ,交AC 边于点E ,如果AB =9,BD =5,AC =3.5,AE =2,那么DE ∥BC .( )3.如图1,321////l l l ,则BFAE DF CE BD AC ==( ) 4.如图2,在△ABC 中,DE ∥BC ,则BCDE EC AE DB AD ==( ) 二、选择题图1 图21.如图3,在△ABC 中,DE ∥BC 交AB 于D ,交AC 于E ,下列不能成立的比例式一定是( )A .EC AE DB AD = B .AE AC AD AB = C .DB EC AB AC = D .BCDE DB AD = 2.如图4,E 是□ABCD 的边CD 上一点,CD CE 31=,AD =12,那么CF 的长为( ) A .4 B .6 C .3 D .123.如图5,□ABCD ,E 在CD 延长线上,AB =10,DE =5,EF =6,则BF 的长为( )A .3B .6C .12D .164.如图6,在ABC 中,AB=3AD, DE//BC, EF//AB, 若AB=9, DE=2, 则线段FC 的长度是( )A. 6B. 5C. 4D. 3图65.如图7,在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于点D 、E , 若AD=4,DB=2,则AE ︰EC 的值为( ) A. 0.5 B. 2 C.32 D. 23 三、填空题 1.如图8, 则 =________, =________;2.如图9,321////l l l ,AM =2,MB =3,CD =4.5,则ND =________,CN =________.3.如图10,D 、E 分别为AB 的三等分点,DF ∥EG ∥BC ,若BC =12,则DF = . EG =________;4.如图11,△ABC 中,DE ∥BC ,若AE ∶EC =2∶3,DB -AD =3,则AD =________; DB =________.21//l l DE AD AC AB 图7 E D C B A 图3 B AC F DE 图4 图5 图11 图10 图9 图8四、解答题1.如图, 已知△ABC 中AB=AC ,AD ⊥BC ,M 是AD 的中点,CM 交AB 于P ,DN ∥CP 交AB 于N , 若AB=6cm ,求AP 的值.2.如图:P 是四边形OACB 对角线的任意一点,且PM ∥CB ,PN ∥CA ,求证:OA :AN=OB :MB3.如图,△ABC 中,AF ∶FD =1∶5,BD =DC ,求:AE ∶EC .4.如图,在△ABC 中,EF ∥CD ,DE ∥BC ,求证:AF ·BD = AD ·FD5.已知直线l 截△ABC 三边所在的直线分别于E 、F 、D 三点,且AD=BE.求证:EF :FD=CA :CB.OP NMC B A。

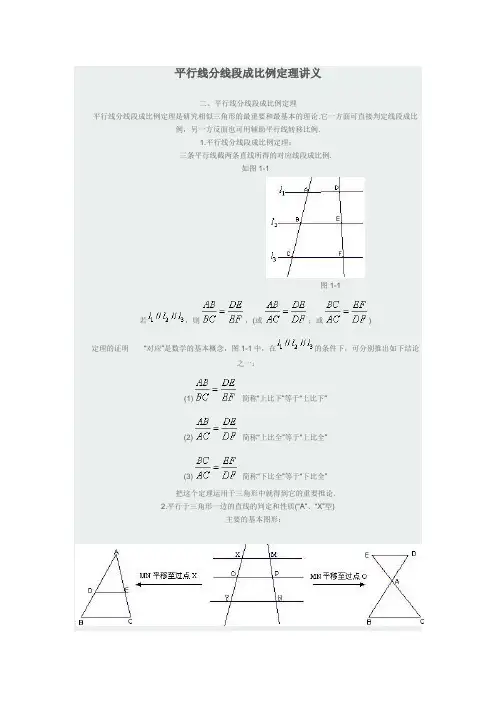
平行线分线段成比例定理讲义
二、平行线分线段成比例定理
平行线分线段成比例定理是研究相似三角形的最重要和最基本的理论.它一方面可直接判定线段成比
例,另一方反面也可用辅助平行线转移比例.
1.平行线分线段成比例定理:
三条平行线截两条直线所得的对应线段成比例.
如图1-1
图1-1
若,则,(或;或)
定理的证明“对应”是数学的基本概念,图1-1中,在的条件下,可分别推出如下结论
之一:
(1)简称“上比下”等于“上比下”
(2)简称“上比全”等于“上比全”
(3)简称“下比全”等于“下比全”
把这个定理运用于三角形中就得到它的重要推论.
2.平行于三角形一边的直线的判定和性质(“A”、“X”型)
主要的基本图形:
1.如图2-1 已知△ABC中AB=AC,AD⊥BC,M是AD的中点,CM交AB于P,DN∥CP
交AB于N,若AB=6cm,求AP的值.
点评:此题利用平行线分线段成比例定理,结合中点定义找出线段的比值,进而求出线段的长.
2.(如图2-2)已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE.
求证:EF:FD=CA:CB.
图2-2又AD=BE
∴.
证法(二) 过E作EP∥BA交CA的延长线于P是解决此问题的第二种辅助线作法.
证法(三) 过D作DN∥BC交AB于N也可解决此问题.。





初中数学成比例线段与平行线分线段成比例编稿老师董志臣一校杨雪二校黄楠审核郑建彬一、考点突破1. 理解并掌握比例的基本性质,成比例线段的定义。
2. 理解平行线分线段成比例的定理及其证明。
3. 应用相关知识解决问题。
二、重难点提示重点:成比例线段及平行线分线段成比例定理的理解。
难点:应用比例性质及平行线分线段成比例定理解决问题。
1. 成比例线段:在同一单位下,四条线段长度为a、b、c、d,其关系为a:b=c:d,那么,这四条线段叫做成比例线段,简称比例线段。
一般地,如果三个数a,b,c满足比例式a:b=b:c,则b就叫做a,c的比例中项。
【注意顺序问题】A. 当题目给出a、b、c、d为成比例线段时,表示有先后顺序之分:为();B. 当题目问a、b、c、d是否为成比例线段时说明没有先后顺序,只要按照一定的顺序,满足比值相等就行。
2. 常用的比例性质:①基本性质:若则ad=bc,可由ad=bc推出a:b=c:d;a:c=b:d;d:b=c:a和d:c=b:a②合比性质:若则;③反比性质:若则;④等比性质:若=…==k, 则 (b+d+…+n≠0)。
3. 平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
定理推论:①平行于三角形一边的直线截其他两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
例题1(青浦区一模)已知:线段a、b、c,且==。
(1)求的值;(2)如线段a、b、c满足a+b+c=27,求a、b、c的值。
思路分析:(1)根据比例的性质得出=,即可得出的值;(2)首先设===k,则a=2k,b=3k,c=4k,利用a+b+c=27求出k的值即可得出答案。
答案:解:(1)∵=,∴=,∴=;(2)设===k则a=2k,b=3k,c=4k,∵a+b+c=27,∴2k+3k+4k=27,∴k=3,∴a=6,b=9,c=12。



衔接教材09 平行线分线段成比例定理 知识点讲解在解决几何问题时,我们常涉及到一些线段的长度、长度比的问题.在数学学习与研究中,我们发现平行线常能产生一些重要的长度比.在一张方格纸上,我们作平行线123,,l l l (如图),直线a 交123,,l l l 于点,,A B C ,2,3AB BC ==,另作直线b 交123,,l l l 于点',','A B C ,不难发现''2.''3A B AB B C BC == 我们将这个结论一般化,归纳出平行线分线段成比例定理: 三条平行线截两条直线,所得的对应线段成比例. 如图,123////l l l ,有AB DE BC EF .当然,也可以得出AB DE AC DF=.在运用该定理解决问题的过程中,我们一定要注意线段之间的对应关系,是“对应”线段成比例.经典例题解析 例1如图,123////l l l ,且2,3,4,ABBC DF 求,DE EF . 解1232////,,3AB DE l l l BC EF 28312,.235235DE DF EF DF ====++ 例2在ABC 中,,D E 为边,AB AC 上的点,//DE BC ,求证:AD AE DE AB AC BC==. 证法(一)://,,,DE BC ADE ABC AED ACB ∴∠=∠∠=∠ ADE ∴∽ABC ,.AD AE DE AB AC BC∴== 证法(二):如图3.1-3,过A 作直线//l BC ,////,l DE BC AD AE AB AC∴=. 过E 作//EF AB 交AB 于D ,得BDEF ,因而.DE BF =//,.AE BF DE EF AB AC BC BC∴==.AD AE DE AB AC BC ∴==从上例可以得出如下结论:平行于三角形的一边的直线截其它两边(或两边的延长线),所得的对应线段成比例. 平行于三角形的一边,并且和其它两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.例3已知ABC ,D 在AC 上,:2:1AD DC =,能否在AB 上找到一点E ,使得线段EC 的中点在BD 上.解假设能找到,如图,设EC 交BD 于F ,则F 为EC 的中点,作//EG AC 交BD 于G . //,EG AC EF FC =,∴EGF CDF ≅,且EG DC =,1//,2EG AD BEG BAD ∴,且1,2BE EG BA AD == E ∴为AB 的中点.可见,当E 为AB 的中点时,EC 的中点在BD 上.我们在探索一些存在性问题时,常常先假设其存在,再解之,有解则存在,无解或矛盾则不存在.例4 在ABC 中,AD 为BAC 的平分线,求证:AB BD AC DC. 证明过C 作CE //AD ,交BA 延长线于E ,//,.BA BD AD CE AE DCAD 平分,,BAC BAD DAC 由//AD CE 知,,BAD E DAC ACE,,E ACE AE AC 即AB BD AC DC. 例4的结论也称为角平分线性质定理,可叙述为角平分线分对边成比例(等于该角的两边之比).实时训练一、单选题1.如图,l 1∥l 2∥l 3,根据“平行线分线段成比例定理”,下列比例式中正确的是()A .AD CE BC DF =B .AD BC BE AF = C .AB CD CD EF = D .AD DF BC CE= 【答案】D【分析】平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例.【详解】解:∵l1∥l2∥l3,∴ADDF =BCCE,即ADBC=DFCE,所以A选项错误,D选项正确;AD AF =BCBE,所以B选项错误;同理C选项也错误.故选D.【点睛】本题考查平行线分线段成比例.2.关于某一点成中心对称的两个图形,下列说法中,正确的个数有()①这两个图形完全重合;②对称点的连线互相平行③对称点所连的线段相等;④对称点的连线相交于一点;⑤对称点所连的线段被同一点平分⑥对应线段互相平行或在同一直线上,且一定相等.A.3个B.4个C.5个D.6个【答案】A【解析】【分析】根据对称中心图形的性质分别判断得出即可.【详解】①这两个图形能够完全重合,此选项错误;②对称点的连线应相交于一点,故此选项错误;③对称点所连的线段不一定相等,此选项错误;④对称点的连线相交于一点,此选项正确;⑤对称点所连的线段被同一点平分,此选项正确;⑥对应线段互相平行或在同一直线上,且一定相等,此选项正确.故正确的有3个.故选:A.【点睛】此题主要考查了对称图形的性质,根据其定义得出是解题关键.二、填空题3.在ABCD中, ∠A的平分线分BC成4cm和3cm的两条线段, 则ABCD的周长为_____.【答案】20cm或22cm;【分析】∠A的平分线分BC成4cm和3cm的两条线段,设∠A的平分线交BC于E点,有两种可能,BE=4或3,证明△ABE是等腰三角形,分别求周长.【详解】解:设∠A的平分线交BC于E点,∵AD∥BC,∴∠BEA=∠DAE,又∠BAE=∠DAE,∴∠BEA=∠BAE∴AB=BE.而BC=3+4=7.①当BE=4时,AB=BE=4,▱ABCD的周长=2×(AB+BC)=2×(4+7)=22;②当BE=3时,AB=BE=3,▱ABCD的周长=2×(AB+BC)=2×(3+7)=20.所以▱ABCD的周长为22cm或20cm.故答案为22cm或20cm.【点睛】主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三、解答题4.证明平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.已知(如图)1l ∥2l ∥3l ,求证:AB DE BC EF.【答案】见解析.【分析】通过作平行,将问题转化为两个相似三角形的对应边成比例的问题,即可得证.【详解】证明:如图,过点E 作直线MN ∥AC ,交1l 、3l 于点G 、H ,∵1l ∥2l ∥3l ,MN ∥AC ,∴四边形ABEG 、BCHE 是平行四边形∴AB=GE,BC=EH,且DGH ,GHF GDF DFH ∠=∠∠=∠∴△DGE ∽△FHE , ∴DE GE AB EF HE BC== 即AB DE BC EF = 原题得证.【点睛】 本题考察了平行线分线段成比例定理及相似三角形的性质与判定.通过条件将问题转化为两个相似三角形的问题是解题关键.5.为更好地理清平行线相关角的关系,小明爸爸为他准备了四根细直木条AB 、BC 、CD 、DE ,做成折线ABCDE ,如图1,且在折点B 、C 、D 处均可自由转出.(1)如图2,小明将折线调节成50B ∠=︒,85C ∠=︒,35D ∠=︒,判断AB 是否平行于ED ,并说明理由;(2)如图3,若35C D ∠=∠=︒,调整线段AB 、BC 使得//AB CD 求出此时B 的度数,要求画出图形,并写出计算过程.(3)若85C ∠=︒,35D ∠=︒,//AB DE ,请直接写出此时B 的度数.【答案】(1)平行,理由见解析;(2)35°或145°,画图、过程见解析;(3)50°或130°或60°或120°【分析】(1)过点C 作CF ∥AB ,根据∠B =50°,∠C =85°,∠D =35°,即可得CF ∥ED ,进而可以判断AB 平行于ED ;(2)根据题意作AB ∥CD ,即可∠B =∠C =35°;(3)分别画图,根据平行线的性质计算出∠B 的度数.【详解】解:(1)AB 平行于ED ,理由如下:如图2,过点C 作CF ∥AB ,∴∠BCF =∠B =50°,∵∠BCD =85°,∴∠FCD =85°-50°=35°,∵∠D =35°,∴∠FCD =∠D ,∴CF ∥ED ,∵CF ∥AB ,(2)如图,即为所求作的图形.∵AB∥CD,∴∠ABC=∠C=35°,∴∠B的度数为:35°;∵A′B∥CD,∴∠ABC+∠C=180°,∴∠B的度数为:145°;∴∠B的度数为:35°或145°;(3)如图2,过点C作CF∥AB,∴CF∥DE,∴∠FCD=∠D=35°,∵∠BCD=85°,∴∠BCF=85°-35°=50°,∴∠B=∠BCF=50°.答:∠B的度数为50°.如图5,过C作CF∥AB,则AB∥CF∥CD,∴∠FCD=∠D=35°,∵∠BCD=85°,∴∠BCF=85°-35°=50°,∵AB∥CF,∴∠B+∠BCF=180°,∴∠B=130°;如图6,∵∠C=85°,∠D=35°,∴∠CFD=180°-85°-35°=60°,∵AB∥DE,∴∠B=∠CFD=60°,如图7,同理得:∠B=35°+85°=120°,综上所述,∠B 的度数为50°或130°或60°或120°.【点睛】本题考查了平行线的判定与性质,解决本题的关键是区分平行线的判定与性质,并熟练运用.6.如图,已知点()A 4,0,()B 0,3,点C 是直线AB 上异于点B 的任一点,现以BC 为一边在AB 右侧作正方形BCDE ,射线OC 与直线DE 交于点P ,若点C 的横坐标为m .()1求直线AB 的函数表达式.()2若点C 在第一象限,且点C 为OP 的中点,求m 的值.()3若点C 为OP 的三等分点(即点C 分OP 成1:2的两条线段),请直接写出点C 的坐标.【答案】(1)3y x 34=-+;(2)48m 25=;(3)2457,2525⎛⎫ ⎪⎝⎭或963,2525⎛⎫ ⎪⎝⎭或96147,2525⎛⎫- ⎪⎝⎭或2493,.2525⎛⎫- ⎪⎝⎭【分析】(1)利用待定系数法即可解决问题;(2)如图,作OG ⊥BC 于G ,OH ⊥OB 于H .只要证明△OCG ≌△CPD ,利用全等三角形的性质可得OG=CD ,由此构建方程即可解决问题;(3)在第一象限和第二象限分两种情形,分别构建方程求出m 即可解决问题;【详解】解:()1设直线AB 的解析式为()y kx b k 0=+≠,把()A 4,0,()B 0,3代入得到{4k b 0b 3+==,解得343k b ⎧=-⎪⎨⎪=⎩,∴直线AB 的解析式为3y x 34=-+.()2如图,作OG BC ⊥于G ,OH OB ⊥于H .四边形BCDE 是正方形,BC//ED ∴,OCG CPD ∠∠∴=,CO CP =,OGC CDP 90∠∠==, OCG ∴≌CPD ,OG CD ∴=,AB 5∴=,OA OB 12OG AB 5⋅∴==,CH m =,4cos BCH cos BAO 5∠∠==,5BC m 4∴=,5CD m 4∴=,512m 45∴=,48m 25∴=.()3①当点C 中第一象限,OC 2PC =时, OCG ∽CPD ,OG ∴:CD 2=:1,55BC m 4=,56m 45∴=,24m 25∴=,∴C (2425,5725)②当点C 中第一象限,PC 2OC =时,. OCG ∽CPD ,OG ∴:CD 1=:2,24CD 5∴=, 5BC m 4=,524m 45∴=,96m 25∴=,∴C (9625,325)③当点C 中第二象限,PC 2OC =时,. OCG ∽CPD ,OG ∴:CD 1=:2,24CD 5∴=, 5BC m 4=-,524m 45∴-=,96m 25∴=-,∴C (9625-,14725).④当点C 中第二象限,OC 2PC =时,OCG ∽CPD ,OG ∴:CD 2=:1,55BC m 4=-, 56m 45∴-=, 24m 25∴=-, ∴C (2425-,9325) 综上所述,满足条件的点C 坐标为2457,2525⎛⎫ ⎪⎝⎭或963,2525⎛⎫ ⎪⎝⎭或96147,2525⎛⎫- ⎪⎝⎭或2493,.2525⎛⎫- ⎪⎝⎭ 【点睛】本题考查一次函数综合题、正方形的性质、锐角三角函数、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题学会用分类讨论的思想思考问题,属于中考压轴题.7.如图在△ABC 中,∠C=90°,AC=3cm ,BC=4cm ,点P 是边BC 上由B 向C 运动(不与点B 、C 重合)的一动点,P 点的速度是1cm/s ,设点P 的运动时间为t ,过P 点作AC 的平行线交AB 与点N ,连接AP ,(1)请用含有t 的代数式表示线段AN 和线段PN 的长,(2)当t 为何值时,△APN 的面积等于△ACP 面积的三分之一?(3)在点P 的运动过程中,是否存在某一时刻的t 的值,使得△APN 的面积有最大值,若存在请求出t 的值并计算最大面积;若不存在,请说明理由.【答案】(1) PN=34t ,AN =5﹣54t ;(2)当t 为43s 时,△APN 的面积等于△ACP 面积的三分之一;(3)t=2时,△PAN 的面积最大,最大值为32. 【解析】【分析】(1)利用勾股定理求出AB ,再利用平行线分线段成比例定理,求出PN 、BN 即可解决问题;(2)由题意:12•PN•PC =13×12•PC•AC ,推出AC =3PN ,由此构建方程即可解决问题; (3)构建二次函数,利用二次函数的性质即可解决问题.【详解】(1)在Rt △ABC 中,∵∠C=90°,AC=3cm ,BC=4cm ,∴AB=(cm ),∵PN ∥AC ,PB=t , ∴PB BC =BN BA =PN AC, ∴4t =5BN =3PN , ∴BN=54t ,PN=34t , ∴AN=AB ﹣BN=5﹣54t . (2)由题意:12•PN•PC=13×12•PC•AC , ∴AC=3PN ,∴3=334⨯t , ∴t=43, ∴当t 为2s 时,△APN 的面积等于△ACP 面积的三分之一.(3)由题意:S △APN =12•PN•PC=12•34t (4﹣t )=﹣38(t ﹣2)2+32, ∵﹣38<0, ∴t=2时,△PAN 的面积最大,最大值为32. 【点睛】本题考查三角形综合题、勾股定理、平行线分线段成比例定理、二次函数的性质等知识,解题的关键是理解题意,学会用方程的思想思考问题,学会构建二次函数解决最值问题,属于中考压轴题.8.西成高铁的开通,使得以前的“蜀道难”变的不再难了,从西安出发的列车,经过4小时左右即可到达成都.周末小华和小亮计划去成都游玩,准备一起去北客站乘车.为了赶时间,他们通过“滴滴打车”叫了一辆快车前往北客站.如图,是小华和小亮一起去北客站乘坐快车的费用y (元)与行驶路程x (千米)之间的函数图象.请你根据以上信息,解答下列问题:(1)求线段AB 所在直线的函数关系式;(2)已知该滴滴打车在高峰时期低速行驶时,每分钟加收0.6元,小华和小亮到达北客站时,共付费43.2元,其中低速行驶8分钟,求小华他们的出发地离北客站有多少千米?【答案】(1) 2.2 3.2y x =+;(2)16千米【详解】解:(1)设线段AB 所在直线的函数关系式为y kx b =+,根据题意,将点()()4,12,9,23A B 代入得412923k b k b +=⎧⎨+=⎩,解得 2.23.2k b =⎧⎨=⎩, ∴线段AB 所在直线的函数关系式为 2.2 3.2y x =+;(2)根据题意得2.2 3.20.6843.2x ++⨯=,解得16x =,答:小华他们的出发地到北客站的路程有16千米.。
平行线分线段成比例判定定理基本模型【摘要】本文将介绍平行线分线段成比例判定定理的基本模型。
在我们将引入该定理的重要性和应用背景。
在首先对定理进行详细说明,然后逐步解释证明步骤,解释相关概念,提供应用举例,并讨论推论拓展。
结论部分将总结归纳所学内容,探讨定理在实际应用中的作用,并展望未来研究方向。
通过本文的阐述,读者将能全面了解平行线分线段成比例判定定理,为进一步的数学学习和应用提供基础。
【关键词】平行线分线段成比例判定定理、引言、定理说明、证明步骤、相关概念解释、应用举例、推论拓展、总结归纳、实际应用、未来研究方向1. 引言1.1 引言平行线分线段成比例判定定理是几何学中的重要定理之一,它解决了平行线与线段之间的关系,为我们在解题过程中提供了便利。
通过这个定理,我们可以轻松判断两条平行线上的线段是否成比例,从而简化问题的复杂度,提高解题效率。
在学习这个定理之前,我们首先需要了解一些基本概念,比如平行线、线段、比例等。
平行线是在同一平面上没有交点的直线,线段是两点之间的连线部分,比例是指两个东西之间的相对大小关系。
这些基本概念是理解平行线分线段成比例判定定理的基础。
在接下来的内容中,我们将详细介绍平行线分线段成比例判定定理的原理和证明步骤,帮助我们更深入地理解这一定理。
我们还将通过相关概念解释、应用举例和推论拓展等部分,进一步探讨这个定理在实际问题中的应用和推广。
通过对平行线分线段成比例判定定理的学习和掌握,我们可以提高解题的效率和准确性,在几何学习中取得更好的成绩。
让我们一起深入探讨这一定理的奥秘,为解决更复杂的几何问题奠定坚实的基础。
2. 正文2.1 定理说明平行线分线段成比例判定定理是初中数学中非常重要的定理之一,它可以帮助我们解决各种与平行线和比例有关的几何问题。
在学习这个定理之前,我们首先要了解什么是平行线和什么是比例。
平行线是在同一个平面内且永远不相交的两条直线,而比例则是指两个量之间的比较关系。
若,则,(或;或) 图1-1 定理的证明定理的证明过A 点作AN ∥DF ,交l 2于M ,交l 3于N 点,连接点,连接 BN 、CM(如图(1-2) 图1-2 ∵∴AM=DE MN=EF 在△ACN 中,有. ∵BM ∥CN ∴S △BCM =S △BMN∴ 亦即亦即如何理解定理结论中“所得对应线段成比例”呢?呢? “对应”是数学的基本概念,图1-1中,在的条件下,可分别推出如下结论之一:名师堂八年级数学第九讲 平行线分线段成比例平行线分线段成比例定理平行线分线段成比例定理是研究平行线分线段成比例定理是研究相似三角形相似三角形的最重要和最基本的理论.它一方面可直接判定线段成比例,另一方反面也可用辅助平行线转移比例. 1.平行线分线段成比例定理:平行线分线段成比例定理:三条平行线截两条三条平行线截两条直线直线所得的对应线段成比例. 如图1-1(1) 简称“上比下”等于“上比下”(2) 简称“上比全”等于“上比全”. (3) 简称“下比全”等于“下比全”把这个定理运用于三角形中就得到它的重要推论. 2.平行于三角形一边的平行于三角形一边的直线直线的判定和性质(“A”、“X”型) 主要的基本图形:主要的基本图形:(图1) 平行线分线段成比例分线段成比例 (图2) 图1、2中,有定理:平行于三角形一边的直线截其他两边或延长线,所得的对应线段成比例(可看作性质1).及其及其逆定理逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边(可看作判定). 以及定理:平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线所截得的三角形与原三角形的三边对应成比例(可看作性质2). 对“A”、“X”型的特征分析:A 点是两相交直线的点是两相交直线的交点交点,D 、E 和B 、C 是两平行线和相交直线的交点,(共5点),其中作比的三点在一条直线上(AD :AB=AE :AC 中,A 、D 、B 在一条直线上,A 、E 、C 在一条直线上.)在作辅助线的时候我们可以观察这些特征.而可以作比的六个点中如果有两个点是同一个点,那么过这个点作平行线往往可以一举多得. 注意点:(1)平行线分线段成比例没有逆定理(2)判断平行线的条件中,只能是被截的两条直线的对应线段成比例(被判断的被判断的 平行线本身不能参与作比例) (3)有些时候我们也要注意图3,DE//BC ,则DF :FE=BG :GC (4)由于平行线分线段成比例定理中,平行线本身没有参与作比例,因此,有关 平行线段的计算问题通常转化到“A”、“X”型中. 典型例题典型例题例1.如图2-1 已知△ABC 中AB=AC ,AD ⊥BC ,M 是AD 的中点,CM 交AB 于P ,DN ∥CP 交AB 于N ,若AB=6cm ,求AP 的值例2.(如图2-2)图2-3 已知已知直线直线截△ABC 三边所在的直线分别于E 、F 、D 三点且AD=BE. 求证:EF :FD=CA :CB. 图2-2 证法(二) 过E 作EP ∥BA 交CA 的延长线于P 是解决此问题的第二种辅助线作法. 证法(三) 过D 作DN ∥BC 交AB 于N 也可解决此问题. 例3.AM 是△ABC 的中线,P 是AM 上任意一点,BP 、CP 的延长线分别交AC 、AB 于E 、D 两点. 求证:DE ∥BC. 分析:如图2-3 练习1.选择题:.选择题:(1)如图,AB∥CD∥EF,则在图中下列关系式一定成立的是( ) A.B.C.DA.2 B.3C.DA.B.C.D.(4)在△ABC中,点D在AB上,点E在AC上,且DE∥BC ,,则等于( ) A.B.C.D..(2)如图,△ABC中,G是BC中点,E是AG中点,CE的延长线交AB于D,则EC:DE的值为( ) .(3)如图,在△ABC中,DE∥BC,则下列,则下列比例比例式成立的是( ) (5)如图,△ABC中,DE∥AC交AB、BC于D、E,如果AB=7cm,AC=5cm,AD=3cm,则DE=( ) A.B.C.DA.B.C.D的面积的,求EC的长. .(6)如图,在△ABC中,如果DE∥BC,DF∥AC,则下列,则下列比例比例式中不正确的是( ) .2.已知:如图,△ABC中,CD是∠ACB的平分线,DE∥BC,AD:DB=2:3,AC=a,求DE的长. 3.已知:如图,△ABC为等边三角形,边长为2,DE∥BC,△BCD的面积是△ABC4.如图,△ABC中,AD是中线,点F在AD上,且AF:FD=1:2,BF的延长线交AC于E,求AE:EC=?能力提升例1 已知:如图5-195-19,,AD 为△ABC 的角平分线,求证:AB∶AC=BD∶DC.例2 求证:求证:等腰三角形等腰三角形底边上任意一点到两腰距离的和等于一腰上的高.即图5-20中,中,AB=AC AB=AC AB=AC,,P 为底边BC 上任意一点,PR⊥AB 于点R ,PQ⊥AC 于点Q ,BH 为腰上的高.求证:证:PQ+PR=BH PQ+PR=BH PQ+PR=BH..分析一 参阅例3的分析一.的分析一.分析二 如图5-225-22,△ACP ,△ACP 和△DCQ 应该全等,反之,只要证明了它们全等,问题就解决了.在这两个三角形中,个三角形中,AC=DC AC=DC AC=DC,∠ACP=60°,∠DCQ=180°-∠A ,∠ACP=60°,∠DCQ=180°-∠A CD CD-∠BCE=180°-60°-60°=60°,从而-∠BCE=180°-60°-60°=60°,从而例3 已知:如图5-215-21,△ABC ,△ABC 中,∠A 为直角.以AB AB,,AC 分别为边向外侧作分别为边向外侧作正方形正方形ABDE ABDE,,ACFG ACFG,线,线段CD CD,,BF 分别与AB AB,,AC 相交于点X ,Y .求证:.求证:AX=AY AX=AY AX=AY..分析一 如图5-215-21((a ),由于AX∥ED,AY∥GF,所以出现了两组成AX∥ED,AY∥GF,所以出现了两组成比例线段比例线段,在这些成比例的线段中,除AX AX,,AY 外,其余的线段都是两个已知正方形的边,因此AX=AY 应该能用应该能用平行线平行线分线段成比例定理得到证明.到证明.分析二 如图5-215-21((b ),连结线段EX EX,,GY GY,得到△CEX ,得到△CEX 和△BGY.这两个三角形的边CE=BG CE=BG,又,又AX 实际等于AY AY,所以△CEX ,所以△CEX 和△BGY 应该有相等的应该有相等的面积面积.反过来,如果证明了这两个三角形面积相等,问题也就解决了.而要证明这两个三角形面积相等,需要进行等积变形.这只要连结线段AD AD,,AF AF,,那么S △ACD =S △CEX ,S △BAF =S △BGY ,所以只需证明S △ACD =S △BAF .但这.但这很简单很简单了.了.例4 已知:如图5-225-22,,C 为线段AB 上任意一点,以AC AC,,BC 分别为边在AB 同侧作等边△ACD 和等边△BCE,线段AE AE,,CD 相交于点P ,线段BD BD,,CE 相交于点Q .求证:.求证:CP=CQ CP=CQ CP=CQ..。
第章 平行线分线段成比例定理定理 三条平行线截两条直线,所得的对应线段成比例.反之亦真.上述定理中的对应线段是指一条直线被三条平行直线截得的线段与另一条直线被这三条平行直线截得的线段对应,对应线段成比例是指同一直线上两条线段的比(部分与部分之比或部分与整体之比)等于另一条直线上与它们对应的线段的比.1定理中的两条直线可以是平行的,也可以是相交的.若是相交的,且交点在三条平行线中的一条上时,则有如下推论:推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,反之亦真.若称经过一点的若干直线为一直线束,则由推论,有如下推论: 推论 一直线束截两条平行线,所得的对应线段成比例. 此时,成比例的线段在乎行的直线上,与推论中成比例的线段在非平行的直线上要区别清楚. 推论 若一直线束中的直线、、上的点、、、、、满足,,则.上述定理及推论在术解某些含有平行线条件(或隐含有平行线条件)的问题时是很方便的.下面从两方面列举一些例子以说明之. .充分利用题设条件中的平行线条件例(年全国初中联赛题)如图,四边形是梯形,点是上底边上一点,的延长线与的延长线交于点.过点作的平行线交的延长线于点,与交于点.证明:.QPM NFEDCA图19-1证明 设与交于点,则由推论, 注意到,有. ① 注意到,有.②由①②得.于是由推论的逆定理知.延长、交于点,则,.从而.例 设凸四边形的对角线、的交点为,过点作的平行线分别交、于点、,交的延长线于点,是以为圆心,以为半径的圆上一点如图所示.求证:. 证明 如图,延长、交于点,则由推论,1沈文选.平行线分线段成比例定理及应用[J].中等数学,2010(5):2—6.COM F P BEADK图19-2注意到,有. 注意到,有.于是,即.亦即.从而.故.例如图,梯形中,对角线和腰相等,是底的中点,是腰的延长线上的点,交于.求证:.BGFMNEDCPA图19-3证明 设交于,延长交于,延长、交于点,则由推论. 注意到,有. 注意到,有. 于是.而,则.又由题设,有. 从而,故. 例 (年全国初中联赛卷题)在锐角中,,、分别是边、上的高,与的延长线交于点,过点作的垂线交于点,过点作的垂线交于点.证明:、、三点共线. 证明 设与交于点,联结并延长交于,延长交于,延长交于,则.。