试用解析法和图解法求出指定截面上的应力及其主应力并画

第二节 平面应力状态如图8-3(a)所示的单元体，因外法线与z 轴重合的平面上其剪应力、正应力均为零，说明该单元体至少有一个主应力的为零，因此该单元体处于平面应力状态。

为便于研究，取其中平面abcd 来代表单元体的受力情况（图8-3b ）。

任意斜截面的表示方法及有关规定如下：（1）用x 轴与截面外法线n 间的夹角α表示该截面。

（2）α得正负号：由x 轴向n 旋转，逆时针转向为正，顺时针转向为负（图8-3b 的α角为正）。

（3）ασ得正负号：拉应力为正，压应力为负（图8-3的x σ、y σ、ασ均为正值）。

（4）ατ得正负号：ατ对截面内此任一点的力矩转向，顺时针转向为正，逆时针转向为负（图8-3的x τ、ατ均为正值，y τ为负值）。

图8-3一、任意斜截面上的应力计算任意斜截面上应力有两种方法：解析法和图解法。

（一）解析法因研究的构件是平衡的，因此从构件内一点取单元体，并从单元体上取一部分（图8-3c ），则该部分也处于平衡。

由平衡条件可以求得平面应力状态下单元体任一斜截面上的应力计算公式ατασσσσσα2sin 2cos 22x yx yx --++= （8-1）ατασστα2cos 2sin 2x yx +-=（8-2）应用上式 计算ασ、ατ时，各已知应力x σ、y σ、x τ和α均用其代数值。

例8-1 求图8-4所示各点应力状态下斜截面上的应力（各应力单位是Mpa ），并用图表示出来。

解 （1） 已知：x σ=30Mpa ，y σ=-40 Mpa ，x τ=60 Mpa ，α=30º，将各数值代入式（8-1）、（8-2）得斜截面上的应力46.3960sin 6060cos 240302403030-=-++-=σ Mpa 31.6060cos 6060sin 2403030=++= τ Mpa将 30σ、 30τ方向画在斜截面上，如图8-4(1-b)所示。

（2）已知：x σ=-80Mpa ，y σ=0 Mpa ，x τ=-40 Mpa ，α=120º，将各数值代入式（8-1）、（8-2）得斜截面上的应力64.54240sin 40240cos 280280120-=+-+-=σ Mpa 64.54240cos 40240sin 280120=--=τ Mpa将 120σ、 120τ方向画在斜截面上，如图8-4(2-b)所示。

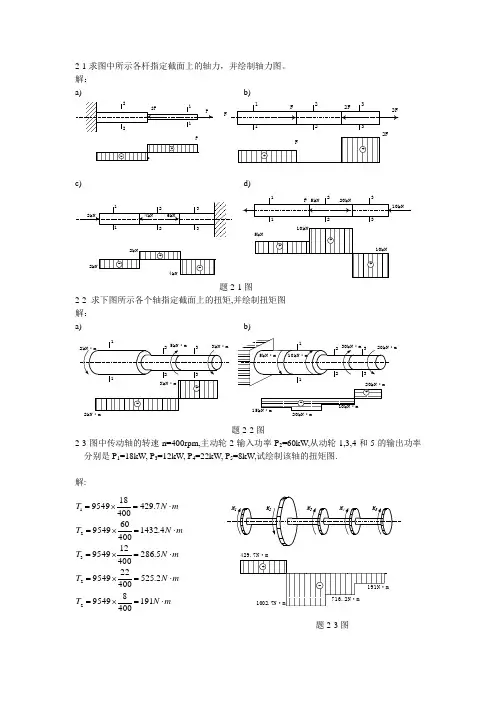
2-1求图中所示各杆指定截面上的轴力，并绘制轴力图。

解：a) b)FFc) d)题2-1图2-2 求下图所示各个轴指定截面上的扭矩,并绘制扭矩图 解：a) b)2kN·m20kN·m题2-2图2-3图中传动轴的转速n=400rpm,主动轮2输入功率P 2=60kW,从动轮1,3,4和5的输出功率分别是P 1=18kW, P 3=12kW, P 4=22kW, P 5=8kW,试绘制该轴的扭矩图. 解:mN T mN T mN T mN T m N T ⋅=⨯=⋅=⨯=⋅=⨯=⋅=⨯=⋅=⨯=191400895492.5254002295495.2864001295494.14324006095497.42940018954922321 题2-3图429.7N·m2-4 求图中所示各梁指定截面上的剪力和弯矩,设q 和F 均为已知.a )b)A qlql 2/2Bc)d)qlF QAM图F Q 图题2-4图2-5试绘制下图所示各梁的剪力图和弯矩图,并求出剪力和弯矩的最大值.设F q l 均为已知.a)b)A F Q2M图F Q 图c)d)F QF Q 图M图e) f)F QM图qlql 2/2ql 2/8F Q M图g)h)F Q M图9ql 2/128F Q M图题2-5图2-6不列方程,绘制下面各梁的剪力图和弯矩图,并求出剪力和弯矩绝对值的最大值.设F 、q 、l 均为已知。

a)b)F Q M图ql 2/2qlF Qc) d)F Q 图M图2FlF Q 图M图e) f)F Q 图M图F Q M图题2-6图2-7绘制下图所示各梁的剪力图和弯矩图,求出|F Q |max 和|M|max ,并且用微分关系对图形进行校核.a) b)F Q 图M图F Q 图M图Flc)d)F Q 图M图2F Q题2-7图2-8试判断图中所示各题的F Q ，M 图是否有错，如有错误清指出错误原因并加以改正。

材料力学习题答案2在图示各单元体中，试用解析法和图解法求斜截面ab 上的应力。

应力的单位为MPa 。

解 (a) 如受力图(a)所示()70x MPa σ=，()70y MPa σ=-，0xy τ=，30α=(1) 解析法计算（注：P217）()cos 2sin 22270707070 cos 6003522x yx y xy MPa ασσσσσατα+-=+--+=+-= ()7070sin cos 2sin 60060.622x yxy MPa ασστατα-+=+=-= (2) 图解法作O στ坐标系, 取比例1cm=70MPa, 由x σ、xy τ定Dx 点, y σ、yx τ定Dy 点, 连Dx 、Dy , 交τ轴于C 点, 以C点为圆心, CDx 为半径作应力圆如图(a1)所示。

由CDx起始, 逆时针旋转2α= 60°,得D α点。

从图中可量得D α点的坐标, 便是ασ和ατ数值。

已知应力状态如图所示，图中应力单位皆为MPa 。

试用解析法及图解法求:(1) 主应力大小，主平面位置；(2) 在单元体上绘出主平面位置及主应力方向；(3) 最大切应力。

解 (a) 受力如图(a)所示()50x MPa σ=，0y σ=，()20xy MPa τ=(1) 解析法 （数P218） 2max 2min 22x y x y xy σσσσστσ+-⎛⎫⎫=±+⎬ ⎪⎭⎝⎭()()225750050020722MPa MPa⎧+-⎪⎛⎫=±+=⎨ ⎪-⎝⎭⎪⎩按照主应力的记号规定()157MPa σ=，20σ=，()37MPa σ=-02220tan 20.8500xyx y τασσ⨯=-=-=---，019.3α=-()13max 5773222MPa σστ-+===(2) 图解法作应力圆如图(a1)所示。

应力圆与σ轴的两个交点对应着两个主应力1σ、3σ 的数值。

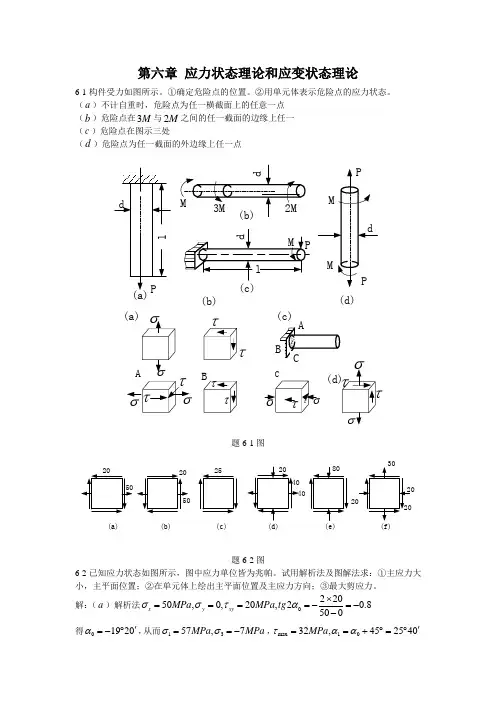
第六章 应力状态理论和应变状态理论6-1构件受力如图所示。

①确定危险点的位置。

②用单元体表示危险点的应力状态。

（a ）不计自重时，危险点为任一横截面上的任意一点 （b ）危险点在3M 与2M 之间的任一截面的边缘上任一 （c ）危险点在图示三处（d ）危险点为任一截面的外边缘上任一点(b)(c)(d)(a)题6-1图(a)(b)(c)(d)(e)(f)题6-2图6-2已知应力状态如图所示，图中应力单位皆为兆帕。

试用解析法及图解法求：①主应力大小，主平面位置；②在单元体上绘出主平面位置及主应力方向；③最大剪应力。

解：（a ）解析法022050,0,20,20.8500x y xy MPa MPa tg σστα⨯====-=--得01920α'=-︒，从而1357,7MPa MPa σσ==-，max 1032,452540MPa ταα'==+︒=︒用图解法，按几何关系可求得0max 240,32MPa ατ=︒=20(c)αααασ((e)(-20)（b ）解析法：150572MPa σ==，35072MPa σ==- 02(20)420.8505tg α-=-==，得01384019202α''=⨯︒=︒， max 32MPa τ== （c ）解析法：13025,25MPa MPa σσ=+==-，022520tg α⨯=-→无穷大，00max 290,45,25MPa αατ=-︒=-︒= （d ）解析法：40,29x y MPa MPa σσ==-，1402011.22MPa σ-=+=，3402071.22MPa σ-==- 02(40)42,40203tg α⨯-=-=+0max 3759,41.2MPa ατ'=-︒=（e ）解析法：1080 4.72MPa σ-==，308084.72MPa σ-==- 022020.5080tg α⨯=-=-+，0022634,1317αα''=-︒=-︒max 44.7MPa τ=（f ）解析法：12030372MPa σ-+=+=，32030272MPa σ-+==- 00022020.8,221840,109202030tg ααα⨯''=-==︒=︒--max 32MPa τ== 6-3在图示应力状态中，试用解析法和图解法求指定斜截面上的应力（应力单位为兆帕）。

应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。

绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。

b = 60 mm ，h = 100 mm 。

解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。

则各点处的应力状态如图示。

2、梁截面惯性矩为点微体上既有正应力又有切应力。

解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。

材料力学习题(1)2-6章材料力学习题第2章2-1 试求出图示各杆Ⅰ—Ⅰ截面上的内力。

2-2图示矩形截面杆，横截面上正应力沿截面高度线性分布，截面顶边各点处的正应力均为MPa100max=σ，底边各点处的正应力均为零。

杆件横截面上存在何种内力分量，并确定其大小（C点为截面形心）。

2-3 试指出图示各单元体表示哪种应力状态。

2-4 已知应力状态如图所示（应力单位为MPa），试用解析法计算图中指定截面的应力。

2-5 试作应力圆来确定习题2-4图中指定截面的应力。

2-6已知应力状态如图所示（应力单位为MPa ），试用解析法求：（1）主应力及主方向；（2）主切应力及主切平面；（3）最大切应力。

2-7 已知应力状态如习题2-6图所示，试作应力圆来确定：（1）主应力及主方向； （2）主切应力及主切平面；（3）最大切应力。

2-8已知构件内某点处的应力状态为两种应力状态的叠加结果，试求叠加后所得 应力状态的主应力、主切应力。

2-9图示双向拉应力状态，σσσ==y x 。

试证明任一斜截面上的正应力均等于σ，而切应力为零。

2-10 已知K 点处为二向应力状态，过K 点两个截面上的应力如图所示（应力单位为MPa ）。

试分别用解析法与图解法确定该点的主应力。

2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。

试确定未知的应力分量y y x xy '''σττ、、的大小与方向。

2-12 图示受力板件，试证明尖角A 处各截面的正应力与切应力均为零。

2-13 已知应力状态如图所示（单位为MPa ），试求其主应力及第一、第二、第三不变量321I I I 、、。

2-14 已知应力状态如图所示（单位为MPa ），试画三向应力圆，并求主应力、最大正应力与最大切应力。

第3章3-1 已知某点的位移分量u = A ， v = Bx +Cy +Dz ， w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。

重庆大学材料力学答案题图所示中段开槽的杆件，两端受轴向载荷P 的作用，试计算截面1-1和2-2上的应力。

已知：P = 140kN ，b = 200mm ，b 0 = 100mm ，t = 4mm 。

题图解：(1) 计算杆的轴力 (2) 计算横截面的面积 (3) 计算正应力(注：本题的目的是说明在一段轴力相同的杆件内，横截面面积小的截面为该段的危险截面)横截面面积A=2cm 2的杆受轴向拉伸，力P=10kN ，求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ，并问m ax τ发生在哪一个截面？ 解：(1) 计算杆的轴力(2) 计算横截面上的正应力 (3) 计算斜截面上的应力(4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此：22πα=， ο454==πα故：m ax τ发生在其法线与轴向成45°的截面上。

（注：本题的结果告诉我们，如果拉压杆处横截面的正应力，就可以计算该处任意方向截面的正应力和剪应力。

对于拉压杆而言，最大剪应力发生在其法线与轴向成45°的截面上，最大正应力发生在横截面上，横截面上剪应力为零）题图所示阶梯直杆AC ，P =10kN ，l 1=l 2=400mm ，A 1=2A 2=100mm 2，E =200GPa 。

试计算杆AC 的轴向变形Δl 。

题图解：(1) 计算直杆各段的轴力及画轴力图 kN 101==P N （拉） kN 102-=-=P N （压）(2) 计算直杆各段的轴向变形mm 2.010010002004001000101111=⨯⨯⨯⨯==∆EA l N l （伸长）mm 4.05010002004001000102222-=⨯⨯⨯⨯-==∆EA l N l （缩短） (3) 直杆AC 的轴向变形m m 2.021-=∆+∆=∆l l l （缩短）(注：本题的结果告诉我们，直杆总的轴向变形等于各段轴向变形的代数和)题图所示结构，各杆抗拉（压）刚度EA 相同，试求节点A 的水平和垂直位移。

台州学院材料力学作业题集专业：班级：姓名：学号：任课教师：前言材料力学是变形体力学的入门课程，是土木工程专业学生必修的技术基础课。

要求学生明确从几何、物理和静力平衡三个方面分析杆件力学问题的基本思路，掌握杆件的强度、刚度和稳定性的基本概念；培养学生具备必要的基础理论知识，比较熟练的计算能力、一定的分析能力和实验能力，为学习结构力学、钢结构、混凝土结构等后续课程提供必要的基础。

为此，为配合课堂教学环节，建筑工程学院材料力学课程组特按教材章节编写了此作业题集，各章包括作图题，简答题，计算题，综合题等题型，重点考查学生对基本概念，基本原理，基本方法的理解和掌握，训练学生的计算能力，建模能力以及思维能力。

建筑工程学院材料力学课程组 2013年6月一、试作出图示各杆的轴力图。

()a P 1=20kN P 3=30kNP 3=10kN二、图示结构中，1、2两杆的横截面直径分别为15mm和20mm，试求两杆的应力。

设两根横梁皆为刚体。

三、图示结构中，AB为刚体，1、2杆的抗拉（压）刚度分别为EA，2EA。

试求两杆的轴力。

四、在图示简易吊车中，BC 为钢杆，AB 为木杆。

木杆AB 的横截面面积21cm 100=A ，许用应力[]MPa 71=σ；钢杆BC 的横截面面积22cm 6=A ，许用应力[]MPa 1602=σ。

试求许可吊重[]F 。

五、图示结构中，BC 由一束直径为2mm 的钢丝组成，若钢丝的许用应力为[]MPa 160=σ，q =20kN/m ，AC 杆长4m 。

试求BC 需由多少根钢丝组成。

BC六、结构尺寸及受力如图所示，AB 可视为刚体，CD 为圆截面钢杆，直径为D=30mm ，材料为Q235钢，许用应力为[]180σ=MPa ，200E GPa =，求许可载荷[]F 。

七、桁架的尺寸及受力如图所示，若F =200kN ，AB 杆的横截面面积A=4000mm 2，试求AB 杆的应力。

八、图示桁架结构，杆AC 由两根L63×10 等边角钢组成，杆CD 由两根L75×10等边角钢组成，已知：L63×10 的横截面为11.657cm 2，L75×10的横截面积为14.126cm 2，[σ]=150MPa 。

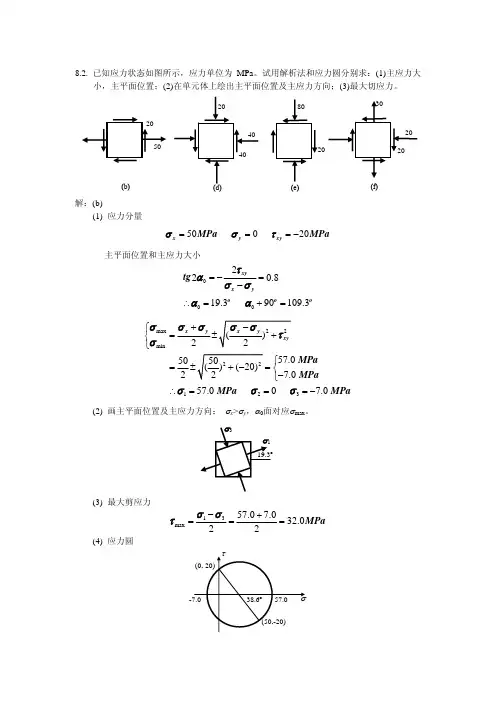
9.1a)b) c) d)9.2单元体各面的应力如图所示(应力单位为MPa ），试用 解析法和图解法计算指定截面 上的正应力和剪应力。

a)解：(1) 解析法：单元体斜截面上的应力公式为ατασστατασσσσσαα2cos 2sin 222cos 22x yx x yx yx sim +-=--++=将图（a ）中各值代入上式，得MPaMPa 1090cos 2090sin 210304090sin 2090cos 2103021030=--==+-++=αατσ（2）图解法在τσ-坐标内，按选定的比例尺，由()20,30-和()20,10分别定出',D D 两点(图b)，以',D D 为直径作圆，即得所求主应力圆。

在应力圆上，将半径CD 沿逆时针方向转动 902=α，到CE 处，所得圆上E 的坐标，即代表单位圆上 45=α斜截面上的应力。

量得MPa MPa 10,40==αατσ（b ）解：(1) 将图（a ）中20,10-==y x σσ， 60,15-==ατx 代入斜截面应力公式，得()()MPa 49.0120sin 15120cos 2201022010=---++-=ασ ()()M P a 49.20120cos 15120sin 22010-=-+-+=ατ （2）图示法应力圆如图（b ）所示，从图中量得，0=ασ，MPa 20-=ατ(1) 解析法将图（a ）中50,30==y xσσ， 150,0-==ατx ，代入斜截面应力公式，得()M P a 35300cos 2503025030=--++=ασ ()M P a 66.8300sin 25030-=--=ατ （2）图解法应力圆如图b)所示，从图中量得MPa 35=εσ，MPa 9-=ατ9.3 单元体各面的应力如图所示（应力单位为MPa ）。

试用解析法和图解法计算主应力的大小及所在截面的方位，并在单元体上画出。

8-9 矩形截面梁如图所示，绘出1、2、3、4点的应力单元体，并写出各点的应力计算式。

解：(1)求支反力R A =,R B = (2)画内力图如图所示。

xPl(-)(+)PlMkN ·m)PPy(-)(-)(+)VkN)题8-9图(3) 求梁各点的正应力、剪应力：(4)画各点的应力单元体如图所示。

9-1 试用单元体表示图示构件的A 、B 的应力单元体。

（a ）解：（1）圆轴发生扭转变形，扭矩如图所示。

111max 222222333333max 442330,22(')[()]448114()121200(0,0)16ZZZ ZzV pA b hh h hP P b M V S Pl hy I I bb h b h b M SM PlW b h σττστστστ==-=-⋅=-⋅⋅-⋅⨯⨯-⋅=⋅=⋅==⋅⨯⨯⨯⨯⋅=====-=-=⨯⨯80A-+16080T (kN ·m )（2）绘制A 、B 两点的应力单元体：A 、B 两点均在圆轴最前面的母线上，横截面上应力沿铅垂方向单元体如图所示：331601020.21680510.216A A t bB t T Pa kPa W T Pa kPaW τπτπ===⨯===-⨯（b ）解：（1）梁发生弯曲变形，剪力、弯矩图如图所示。

-+120VkN)40MkN ·m)+120402060题9-1（b ）（2）绘制A 、B 两点的应力单元体：A 点所在截面剪力为正，A 点横截面的剪力为顺时针，同时A 点所在截弯矩为正下拉，而A 点是压缩区的点。

B 点所在截面剪力为负，B 点横截面的剪力为逆时针，同时B 点所在截弯矩为正下拉，而B 点是拉伸区的点。

单元体如图所示：333.3333.60100.0537.50.1200.21212010(0.1200.050.075) 5.6250.1200.20.1201220100.0512.50.1200.2124010(0.1200.05A A A tA z A A tB B B t B z B B t M y Pa MPaI V S Pa MPaI b M y Pa MPaI V S I bστστ⨯=-⋅=-⨯=-⨯⋅⨯⨯⨯⨯=⋅==⋅⨯⨯⨯=⋅=⨯=⨯⋅-⨯⨯⨯⨯=⋅=⋅g g 30.075) 1.8750.1200.20.12012Pa MPa=-⨯⨯9-2（c解：(1)由题意知：30,20.5030ox x y MP MPa MP στσα==-==，，。

材料力学习题第2章2-1 试求出图示各杆件中Ⅰ—Ⅰ截面上的内力。

2-2图示矩形截面杆，横截面上正应力沿截面高度线性分布，截面顶边各点处的正应力均为MPa 100max =σ，底边各点处的正应力均为零。

杆件横截面上存在何种内力分量，并确定其大小（C 点为截面形心）。

2-3 试指出图示各单元体表示哪种应力状态。

2-4 已知应力状态如图所示（应力单位为MPa ），试用解析法计算图中指定截面的应力。

2-5 试作应力圆来确定习题2-4图中指定截面的应力。

2-6已知应力状态如图所示（应力单位为MPa ），试用解析法求：（1）主应力及主方向；（2）主切应力及主切平面；（3）最大切应力。

2-7 已知应力状态如习题2-6图所示，试作应力圆来确定：（1）主应力及主方向； （2）主切应力及主切平面；（3）最大切应力。

2-8已知构件内某点处的应力状态为两种应力状态的叠加结果，试求叠加后所得 应力状态的主应力、主切应力。

2-9图示双向拉应力状态，σσσ==y x。

试证明任一斜截面上的正应力均等 于σ，而切应力为零。

2-10 已知K 点处为二向应力状态，过K 点两个截面上的应力如图所示（应力单位为MPa ）。

试分别用解析法与图解法确定该点的主应力。

2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。

试确定未知的应力分量y y x xy '''σττ、、的大小与方向。

2-12 图示受力板件，试证明尖角A 处各截面的正应力与切应力均为零。

2-13 已知应力状态如图所示（单位为MPa ），试求其主应力及第一、第二、第三不变量321I I I 、、。

2-14 已知应力状态如图所示（单位为MPa ），试画三向应力圆，并求主应力、最大正应力与最大切应力。

第3章3-1 已知某点的位移分量u = A ， v = Bx +Cy +Dz ， w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。

试用解析法和图解法求出指定截面上的应力及其主应力并画(总6页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、在图示应力状态中，试用解析法和图解法求出指定截面上的应力及其主应力并画主单元体（应力单位为MPa）。

2二、受力某点两平面上的应力如图示，求其主应力。

应力单位为MPa。

3三、在通过一点的两个平面上，应力如图所示，单位为MPa。

试分别用解析法和图解法求其主应力的数值及主平面的位置，并绘制主单元体。

4四、试求图示应力状态的主应力及最大切应力。

应力单位为MPa。

五、受载荷系统I作用时，某点的应力状态如图()a所示；受载荷系统II作用时，该点的应力状态如图()b所示。

试求构件在这两组载荷共同作用下（设仍在线弹性范围内）该点的应力状态（用单元体表示），并求出其主应力及最大切应力。

1τ()a b56六、悬臂梁右边部分作用有未知的分布力()x q ，现测得距自由端l 处的中性层上A 点与轴线成045方向的线应变4104.2-⨯=αε（045=α）。

材料的弹性模量GPa 210=E ，泊松比28.0=μ，mm 30=b ，mm 60=h 。

试求分布力()x q 的合力大小及方向。

七、一受扭圆轴如图所示，其弹性模量GPa 200=E ，泊松比28.0=μ。

现测得645106500-⨯=ε，试求扭矩e M 。

h ()x q A 045b x7八、已知受力构件表面某点处沿三个方向的线应变为：60102670-⨯-=ε，645105700-⨯-=ε，69010790-⨯=ε。

材料的弹性模量GPa 210=E ，泊松比3.0=μ，试求该点的主应力。

例1：求指定截面上的正应力和剪应力、单元体的主应力、主平面，将主应力标在主平面上。

解：σx =－20 σy =30 τxy =20 α=300MPa8.24 60sin 2060cos 230202302030-=-－－＋＋－＝σ MPa7.11 60cos 2060sin 2302030-=+－－＝τ 请学生将σα、τα标在单元体上。

主应力、主平面 MPaMPa2737 20230202302022min max -+⎪⎭⎫ ⎝⎛-±+=＝－－σσ1=37 σ2=0 σ3=－2730202022tan 0-⨯-=－α α0 ＝19.30 α0 +90 ＝109.30将主平面标在单元体上，如图所示。

确定σ1作用平面：（1）σ1与σx 、σy 中代数值最大的应力的夹角一定小于450； （2）根据单元体的变形趋势确定。

例2：已知梁上的M 、Q ，试用单元体表示截面上1、2、3、4点的应力状态。

解：1点 zx W M -=σ 所以 x σσσσ===3210 2点 AQ 23＝τ τσστσ－===321 03点 z x I My -=σ b I QS z *=τ 223122τσσσ+⎪⎭⎫⎝⎛±=x x σ2=04点 zx W M=σ 所以 x σσσσ===123τ例3： 图示结构，已知E 、μ，现测得K 点与轴线成450方向上的应变为ε，试确定梁上的荷重P 。

（设工字钢型号已知）解：K 点处于纯剪切状态，b I QS z *＝τ 则K 点的主应力为σ1＝τ、σ2＝0、σ3＝－τ例4 工字形截面梁如图所示，已知[σ]=160MPa [τ]=100MPa 试按第三强度理论选择工字钢型号。

解：1作Q 、M 图，B 、C 为危险截面，Q max =20kN 、M max ＝84kNm 2选择型号b 点由正应力强度条件：[]3maxmax 525 cm W W M z z≥≤=σσ 取28b 工字钢 a 点校核剪应力强度：[]ττ<==*MPa bI S Q z 6.78max maxστc 点腹板与翼缘交界处： M P aI Myz142＝σ M P ab I QS z 6.57==*τ 用第三强度理论校核：MPa MPa r 1601734223>=+=τσσ 应加大截面尺寸结合上述例题总结强度计算中常常遇到的三类危险点： 第一类：正应力最大点，通常为单向应力状态； 第二类：剪应力最大点，通常为纯剪切状态；第三类：正应力、剪应力都较大的点，用强度理论计算。