确定主应力大小和方向问题分析

在以三向应力状态最大主应力方向计算为主题的文章中，我们需要首先了解三向应力状态及其计算方法，然后深入讨论最大主应力方向的计算方式和重要性。

接下来，我们可以探讨该主题对工程、地质或其他领域的影响，以及我们个人对这一主题的看法和理解。

三向应力状态是指一个材料或结构受到的三个方向上的应力作用。

在工程和地质领域中，我们常常需要对材料或地质构造的三向应力状态进行分析和计算，以确保其稳定性和安全性。

三向应力状态的计算可以通过各种方法和公式进行，其中最常用的包括Mohr圆和三向应力变形方程等。

通过这些计算，我们可以得到材料或地质构造中的最大主应力方向，这对于预测和防范可能的破坏或变形具有重要意义。

让我们深入探讨最大主应力方向的计算方式。

最大主应力方向通常是材料或地质构造中应力最大的方向，它决定了材料或结构的破坏模式和破坏时机。

最大主应力方向的计算需要通过三向应力状态的分解和转换来实现，其中包括求解Mohr圆上的最大主应力角度和大小等步骤。

计算最大主应力方向不仅可以帮助我们预测材料或结构可能出现的破坏情况，还可以指导我们优化设计和改进工程实践。

在文章的后半部分，我们可以探讨三向应力状态最大主应力方向计算在工程、地质或其他领域的应用和意义。

工程中的材料强度设计和地质构造的稳定性分析都离不开对最大主应力方向的计算和预测。

我们也可以共享一些具体的案例或实践经验，来展示这一主题对实际工作的影响。

我们可以结合个人经历和观点，对这一主题进行全面、深刻和灵活的理解和总结，以提高读者对该主题的认识和理解。

通过对三向应力状态最大主应力方向计算的深度和广度的探讨，我们可以更全面地理解这一主题的重要性和应用价值。

在文章中，我们通过介绍基本概念、计算方法和应用意义，为读者提供了一份有价值的信息。

通过共享个人观点和理解，我们也希望能够激发读者对这一主题的兴趣，并促进更深入的讨论和探索。

三向应力状态最大主应力方向的计算在工程、地质和其他领域中具有重要的应用价值。

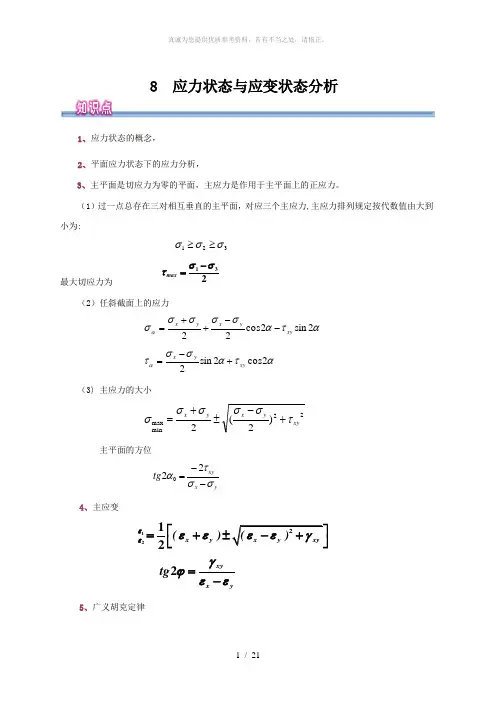
8 应力状态与应变状态分析1、应力状态的概念，2、平面应力状态下的应力分析，3、主平面是切应力为零的平面，主应力是作用于主平面上的正应力。

（1）过一点总存在三对相互垂直的主平面，对应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=（2）任斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=（3) 主应力的大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面的方位y x xytg σστα--=2204、主应变122122x y x y xy xyx y()()tg εεεεεεγγϕεε⎡=+±-+⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1x z y y E σσμσε+-=)]([1y x z z E σσμσε+-=G zxzx τγ=G yzyz τγ=，G xyxy τγ=6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。

”8.1 试画出下图8.1(a)所示简支梁A 点处的原始单元体。

图8.1[解]（1）原始单元体要求其六个截面上的应力应已知或可利用公式直接计算，因此应选取如下三对平面：A 点左右侧的横截面，此对截面上的应力可直接计算得到；与梁xy 平面平行的一对平面，其中靠前的平面是自由表面，所以该对平面应力均为零。

再取A 点偏上和偏下的一对与xz 平行的平面。

截取出的单元体如图8.1(d)所示。

(2)分析单元体各面上的应力:A 点偏右横截面的正应力和切应力如图8.1(b)、(c)所示，将A 点的坐标x 、y 代入正应力和切应力公式得A 点单元体左右侧面的应力为：z M y I σ=bI QS z z*=τ由切应力互等定律知,单元体的上下面有切应力τ ；前后边面为自由表面，应力为零。

实验一拉伸实验一、实验目的1．测定低碳钢(Q235)的屈服点σ，强度极限bσ，延伸率δ，s断面收缩率ψ。

2．测定铸铁的强度极限σ。

b3．观察低碳钢拉伸过程中的各种现象（如屈服、强化、颈缩等），并绘制拉伸曲线。

4．熟悉试验机和其它有关仪器的使用。

二、实验设备1．液压式万能实验机；2．游标卡尺；3．试样刻线机。

三、万能试验机简介具有拉伸、压缩、弯曲及其剪切等各种静力实验功能的试验机称为万能材料试验机，万能材料试验机一般都由两个基本部分组成；1）加载部分，利用一定的动力和传动装置强迫试件发生变形，从而使试件受到力的作用，即对试件加载。

2）测控部分，指示试件所受载荷大小及变形情况。

四、试验方法1．低碳钢拉伸实验（1）用画线器在低碳钢试件上画标距及10等分刻线，量试件直径，低碳钢试件标距。

（2）调整试验机，使下夹头处于适当的位置，把试件夹好。

（3）运行试验程序，加载，实时显示外力和变形的关系曲线。

观察屈服现象。

（4）打印外力和变形的关系曲线，记录屈服载荷F s=22.5kN，最大载荷F b =35kN。

（5测量拉断后的标距长L1，表1-3。

低碳钢的拉伸图如图所示2．铸铁的拉伸其方法步骤完全与低碳钢相同。

因为材料是脆性材料，观察不到屈服现象。

在很小的变形下试件就突然断裂（图1-5），只需记录下最大载荷F b=10.8kN即可。

的计算与低碳钢的b计算方法相同。

六、试验结果及数据处理表1-2 试验前试样尺寸表1-3 试验后试样尺寸和形状根据试验记录，计算应力值。

低碳钢屈服极限 MPa 48.28654.78105.2230=⨯==A F s s σ低碳钢强度极限 MPa 63.44554.78103530=⨯==A F b b σ低碳钢断面收缩率 %6454.7827.2854.78%100010=-=⨯-=A A A ψ低碳钢延伸率 %25100100125%100001=-=⨯-=L L L δ 铸铁强度极限 MPa 53.13754.78108.1030=⨯==A F b b σ七、思考题1． 根据实验画出低碳钢和铸铁的拉伸曲线。

弯扭组合梁主应力大小及方向的测定1 实验目的⑴、用电测方法测定弯扭组合变形梁主应力大小及方向。

⑵、掌握主应力大小及方向的理论和实测计算公式，并进行比较计算其误差值。

⑶、掌握电阻应变花的应用。

2 仪器和设备⑴、50KN微机控制电子万能试验机。

⑵、TS3861静态电阻应变仪。

⑶、游标卡尺。

3 实验原理及装置图8－1 弯扭组合梁示意图图8－2 Ⅰ-Ⅰ截面弯扭组合梁为一空心薄壁园轴，材料为45号钢，其弹性常数为：E=210GPa，μ=0.28，横截面尺寸，外经D=30mm，内径d=26mm。

其一端固定，另一端装一固定加力臂端，轴与力臂端的轴线相互垂直，并且在同一水平面内。

离悬臂端加载点的垂直距离135mm处I-I截面为被测位置，如图1。

在此处园轴表面的前后、上下（图8-2）所示的A、C、B、D四个被测位置上，每处粘贴一枚三轴直角应变花，如图8-3所示。

共计12片应变片，供不同的测试目的选用。

当加力臂端作用载荷P后，园轴发生扭转与变形的组合变形，薄壁园轴横截面上便有内力素：弯矩、扭矩和剪力。

在I-I 截面的A 、C 、B 、D 被测四点上，其单元体上应力状态如图8-4所示。

一．实验测定主应力大小及方向弯扭组合变形构件表面上一点处于平面应力状态，由应力-应变广义胡克定律可知，为了确定一点处的主应力，可在该点处粘贴一直角应变花，该直角应变花由三个应变片组成，既由+45o方向的应变片、O o方向的应变片和-45o方向的应变片组成。

只要用静态电阻应变仪将这三个方向上的线应变测出，代入公式既可计算出主应变的大小和方向。

为了兼测其它实验值，本实验采用直角应变花，并使中间的应变片方向与园轴母线一致，另外两片分别与母线成±45o角，在A 、B 、C 、D 四个测点分别粘贴四枚应变花。

根据被测点三个方向应变值ε45°、ε0°、ε-45° ，计算主应力大小和方向公式分别为：245020454545maxmin )()()1(2)()1(2o o o o o o EE εεεεμεεμσ-+-+⋅±++=-- ……(8—1)Tan2ɑ0=oooo o 4545454502εεεεε----- ……… (8—2)式中ɑ。

确定主应力大小和方向问题分析基础部秦定龙一问题的提出在工程结构设计中，为了全面评价梁的强度安全，确保工程结构万无一失，经常要遇到计算结构中的主应力的大小和确定主应力的方向问题，以便于分析结构破坏的原因，或者合理布置结构形式，或者正确布置结构内的受力钢筋等。

图一(a)所示的钢筋混凝土简支梁，为什么会在轴线以下部分出现斜裂缝而破坏?图一(b)所示的铸铁试件在受到压缩或扭转时，为什么会沿与轴线成的斜面上发生破坏?这些都与结构内的主应力大小和方向有关。

在图二(a)中，钢筋混凝土简支梁的两组主应力轨迹线是根据主应力的方向绘制出来的，而图二(b)中梁内的弯起钢筋和纵向受力钢筋则是根据图二(a)中梁的主应力轨迹线布置的。

图一（a）q(a)图二(b)上述情况说明，在对结构进行强度分析或计算时，都要涉及到结构内主应力大小的计算和确定主应力方向的问题。

一般情况下，主应力的大小可按特定的公式算出来，而在确定应力的方向时，人们往往不容易正确确定出来。

本文就怎样快速准确确定主应力大小和方向作阐述和介绍。

二主应力大小及方向的确定方法图三表示从某一构件中取出的单元体，设它处于平面应力状态下。

假定在一对竖向平面上的正应力为σ,切应力为τ；在一对水平面上的正应力为σy，切应力为τy，它们的大小和方向已经求出。

现要求出这个单元体的最大正应力、最小正应力即主应力的大小和方向。

对应力σ、τ和角度α的正负号规定如下：正应力(或主应力)以拉应力为正，压应力为负；切应力对单元体内的任一点以顺时针转为正，以反时针转时为负；角度α以从x轴的正向出发量到截面的外法成n是反时针转为正，是顺时针转为负。

按照上述的规定，可以判断出，、、及是正值；是正值，是正值，角是负值。

（a）主应力的确定方法有两种：一种是解析法，一种是应力圆法。

下面分别讨论之。

1．确定主应力大小和主平面位置的解析法(b)图三根据对主应力的定义，进行严格的数学推导，得出计算平面应力状态下单元的主应力公式如下： (1)由式(1)可以看出，有两个根。

确定主应力大小与方向问题分析基础部秦定龙一问题得提出在工程结构设计中，为了全面评价梁得强度安全，确保工程结构万无一失,经常要遇到计算结构中得主应力得大小与确定主应力得方向问题, 以便于分析结构破坏得原因,或者合理布置结构形式，或者正确布置结构内得受力钢筋等。

图一（a）所示得钢筋混凝土简支梁,为什么会在轴线以下部分出现斜裂缝而破坏？图一(b)所示得铸铁试件在受到压缩或扭转时,为什么会沿与轴线成得斜面上发生破坏?这些都与结构内得主应力大小与方向有关。

在图二(ａ）中,钢筋混凝土简支梁得两组主应力轨迹线就是根据主应力得方向绘制出来得，而图二(b)中梁内得弯起钢筋与纵向受力钢筋则就是根据图二（ａ)中梁得主应力轨迹线布置得。

图一(a）q(ａ)图二（ｂ）上述情况说明，在对结构进行强度分析或计算时，都要涉及到结构内主应力大小得计算与确定主应力方向得问题.一般情况下,主应力得大小可按特定得公式算出来,而在确定应力得方向时，人们往往不容易正确确定出来。

本文就怎样快速准确确定主应力大小与方向作阐述与介绍。

二主应力大小及方向得确定方法图三表示从某一构件中取出得单元体,设它处于平面应力状态下。

假定在一对竖向平面上得正应力为,切应力为;在一对水平面上得正应力为y,切应力为y,它们得大小与方向已经求出。

现要求出这个单元体得最大正应力、最小正应力即主应力得大小与方向。

对应力、与角度得正负号规定如下：正应力(或主应力)以拉应力为正，压应力为负;切应力对单元体内得任一点以顺时针转为正,以反时针转时为负；角度以从ｘ轴得正向出发量到截面得外法成n就是反时针转为正,就是顺时针转为负.按照上述得规定,可以判断出,、、及就是正值；就是正值,就是正值，角就是负值。

（ａ)主应力得确定方法有两种：一种就是解析法,一种就是应力圆法．下面分别讨论之。

1。

确定主应力大小与主平面位置得解析法(b)图三根据对主应力得定义,进行严格得数学推导,得出计算平面应力状态下单元得主应力公式如下:……(１）由式(１)可以瞧出, 有两个根。

一、实验目的1. 了解薄壁圆管在弯扭组合变形作用下的应力分布规律；2. 掌握应变花的粘贴和测量方法；3. 培养学生分析问题、解决问题的能力。

二、实验原理薄壁圆管在弯扭组合变形作用下，其内力有弯矩、剪力和扭矩。

根据材料力学理论，薄壁圆管在受力时，截面上的应力分布满足平面应力状态。

本实验采用应变花测量方法，通过测量薄壁圆管表面应变，进而计算出主应力的大小和方向。

三、实验仪器与设备1. 弯扭组合实验装置；2. YJ-4501A/SZ静态数字电阻应变仪；3. 薄壁圆管（材料为铝合金）；4. 应变花（三轴450应变花）；5. 粘贴应变花的胶带。

四、实验内容及方法1. 准备工作（1）将薄壁圆管加工成所需形状，并在圆管上确定A、B、C、D四个测点；（2）将应变花按照450、00、450方向粘贴在A、B、C、D四个测点上；（3）连接应变仪和实验装置，确保信号传输正常。

2. 实验步骤（1）加载：按照实验要求，对薄壁圆管进行弯扭组合加载，使圆管产生弯扭变形；（2）测量：启动应变仪，记录应变仪输出的应变值；（3）数据处理：根据应变值，利用应变-应力换算关系计算出主应力的大小和方向；（4）分析：对比不同测点的应力分布，分析薄壁圆管在弯扭组合变形作用下的应力分布规律。

五、实验结果与分析1. 实验数据根据实验数据，得到以下结果：（1）A测点：主应力大小分别为σ1=103.6 MPa，σ2=67.2 MPa，σ3=0 MPa；主应力方向分别为θ1=10.5°，θ2=90°，θ3=179.5°；（2）B测点：主应力大小分别为σ1=104.5 MPa，σ2=67.8 MPa，σ3=0 MPa；主应力方向分别为θ1=11.2°，θ2=90°，θ3=179.2°；（3）C测点：主应力大小分别为σ1=102.4 MPa，σ2=65.9 MPa，σ3=0 MPa；主应力方向分别为θ1=9.8°，θ2=90°，θ3=179.2°；（4）D测点：主应力大小分别为σ1=103.2 MPa，σ2=66.4 MPa，σ3=0 MPa；主应力方向分别为θ1=10.2°，θ2=90°，θ3=179.4°。

主应力法的基本原理
主应力法是一种用于确定地下岩石中主应力方向和大小的地应力分析方法。

它是地质工程学和岩石力学领域中最常用的手段之一，被广泛应用于地质灾害评价、岩石工程设计与施工等方面。

1.地下岩石中的主应力由岩石应力体系中各个应力面上的最大围压应力和最小围压应力决定。

主应力的方向是岩石中最大围压应力的方向，而主应力的大小则由最大和最小围压应力之差确定。

2.主应力法的基本假设是地下岩石是各向异性的弹性体，在一定的应力作用下呈现出塑性行为。

这意味着主应力法适用于岩石的非线性弹塑性行为。

3.主应力法的核心内容是通过不同的实验方法和测量手段来确定主应力方向和大小。

常见的方法包括岩石颜色法、断裂面关系法、松矿法、沉陷法、钻孔法等。

4.主应力法需要考虑的前提条件包括岩石的应力性质、岩石的缺陷和不均匀性、地下水的压力等。

这些条件对主应力方向和大小的测定起到重要的影响。

5.主应力法的应用可以帮助岩石工程设计者确定最佳的施工方案和支护结构，从而减少施工过程中出现的地质灾害风险。

总之，主应力法是一种基于地应力分析的方法，通过测量和评估地下岩石的主应力方向和大小，为岩石工程设计和施工提供科学依据。

它在岩土工程领域中有着广泛的应用前景，可以有效地提高岩石工程的施工安全性和效率。

主应力大小和方向实测值与理论值的差别误差主要由以下因素造成：
1、一些固定不变的系统误差。

如砝码重量不均匀、加力臂与圆筒的垂直度、几何尺寸的不准确、长导线电阻、应变片灵敏系数误差、残余应变等均会对实验精度带来影响。

2、加载不均匀，造成读数误差。

由于杠杆加载机构与薄壁圆筒经组合而成，当杠杆不水平时杠杆支点上的刀口与刀垫、撬动点拉杆的刀口与刀垫相互不垂直，荷载的作用线产生了倾斜，不能完好的实现弯扭组合作用。

扩展资料：
提高实验精度的措施和建议：
1、力求做到接到同一桥路的应变片的种类、规格、长度和引线路径均相同，应该注意避开电磁场的干扰或采用屏蔽措施；应尽量选用栅长大的应变片，这样横向效应影响会有所减小；对于一些不可避免的系统误差，可通过系数修正的方式来提高实验数据的可靠性。

2、改进实验设备，如砝码加载不够平稳、精确，可改用手轮螺旋无级加载。

3、对实验配套设备做好定期维护，保证需要时能正常工作。