当前位置：文档之家 › 运筹学第二章-线性规划

运筹学第二章-线性规划

  • 格式：ppt
  • 大小：4.38 MB
  • 文档页数：37

下载文档原格式

  / 37

合集下载

管理运筹学第二章 线性规划的图解法

管理运筹学第二章 线性规划的图解法

B、约束条件不是等式的问题：
若约束条件为 ai1 x1+ai2 x2+ … +ain xn ≤ bi 可以引进一个新的变量si ，使它等于约束右 边与左边之差 si=bi–(ai1 x1 + ai2 x2 + … + ain xn ) 显然，si 也具有非负约束，即si≥0， 这时新的约束条件成为 ai1 x1+ai2 x2+ … +ain xn+si = bi
第二章 线性规划 的图解法
一、线性规划的概念 二、线性规划问题的提出 三、线性规划的数学模型 四、线性规划的图解法 五、线性规划解的情况 六、LP图解法的灵敏度分析
一、线性规划的概念
线性规划Linear Programming 简称LP，是一 种解决在线性约束条件下追求最大或最小的 线性目标函数的方法。 线性规划的目标和约束条件都可以表示成线 性的式子。
max z 3 x1 2 x2
2 x1 x2 ≤ 10 设备B台时占用 s.t. x1 x2 ≤ 8 x , x ≥ 0 产量非负 1 2
决策变量 （decision variable） 目标函数 （objective function） 约束条件 （subject to）

-ai1
x1-ai2 x2- … -ain xn = -bi 。
例1.3：将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x 1 , x 2 , x3 ≥ 0

第二章线性规划

第二章线性规划



线性规划要研究的两类问题中都包含有约束条件和目 标函数。用数学的方式描述，规划的目的就是在给定 的限制条件（或称约束条件）下，求目标函数的极值 问题（包括极小值和极大值）。
2
线性规划的数学模型
3
解： 设产品 的产量为：1 , 产品 的产量为：x2 x
4
5
6
7

配料问题：由若干种不同价格、不同成分含量的原料，用 不同的配比混合调配出一些不同规格的产品，在原料的供 应量限制和保证产品成分含量的前提下，如何进行配料来 获取最大利润或使总成本最低。
15
2.2.3 线性规划求解的可能结局
1、有唯一的最优解
2、有无穷多个最优解 （将目标函数改为 z=4x1+3x2 ）
x2
max z 4 x1 3 x2 x1 2 x2 5 2 x x 4 1 2 s.t. 4 x1 3 x2 9 x1 , x2 0
3x1 2 x2 4 x3 3
3x1 2 x2 4 x3 xs 3
剩余变量
变量xs实际上是原式左端减去右端的差，即 ：
xs 3x1 2 x2 4 x3 3
当约束条件是“ ”型的不等式时，只要将该约 束条件左端减去一个非负的剩余变量即可化为等式。 无论是松弛变量还是剩余变量在决策中都不产生实际价 值，因此它们在目标函数中的系数都应该为零。有时也将松 29 弛变量和剩余变量统称为松弛变量。
2x1+x2=4 D C
x1+2x2=5 B 4x1+3x2=9 O A x1
16
3、无界解
指线性规划问题有可行解，但是 在可行域，目标函数值是无界的， 因而达不到有限最优值。因此线 性规划问题不存在最优解。

128499-管理运筹学-第二章线性规划-习题

128499-管理运筹学-第二章线性规划-习题

128499-管理运筹学-第⼆章线性规划-习题11（2），12,14,18 习题2-1 判断下列说法是否正确：（1）任何线性规划问题存在并具有惟⼀的对偶问题； T （2）对偶问题的对偶问题⼀定是原问题；T（3）根据对偶问题的性质，当原问题为⽆界解时，其对偶问题⽆可⾏解，反之，当对偶问题⽆可⾏解时，其原问题具有⽆界解；F（4）若线性规划的原问题有⽆穷多最优解，则其对偶问题也⼀定具有⽆穷多最优解；（5）若线性规划问题中的b i ，c j 值同时发⽣变化，反映到最终单纯形表中，不会出现原问题与对偶问题均为⾮可⾏解的情况；（6）应⽤对偶单纯形法计算时，若单纯形表中某⼀基变量x i <0，⼜x i 所在⾏的元素全部⼤于或等于零，则可以判断其对偶问题具有⽆界解。

（7）若某种资源的影⼦价格等于k ，在其他条件不变的情况下，当该种资源增加5个单位时，相应的⽬标函数值将增⼤5k ；（8）已知y i 为线性规划的对偶问题的最优解，若y i >0，说明在最优⽣产计划中第i 种资源已经完全耗尽；若y i =0，说明在最优⽣产计划中的第i 种资源⼀定有剩余。

2-2将下述线性规划问题化成标准形式。

≥≥-++-≤+-+-=-+-+-+-=⽆约束43214321432143214321,0,,232142224.5243max )1(x x x x x x x x x x x x x x x x st x x x x z2-3分别⽤图解法和单纯形法求解下述线性规划问题，并对照指出单纯形表中的各基可⾏解对应图解法中可⾏()≥≤≤-+-=++-+-=⽆约束321321321321,0,0624.322min 2x x x x x x x x x st x x x z 域的哪⼀顶点。

()≥≤+≤++=0,825943.510max 121212121x x x x x x st x x z ()≥≤+≤++=0,24261553.2max 221212121x x x x x x st x x z 2-4已知线性规划问题，写出其对偶问题：543212520202410max x x x x x z ++++=≥≤++++≤++++057234219532..5432154321j x x x x x x x x x x x t s≥≥+≥+≥+++≥++0226332..31434321421j x x x x x x x x x x x x t s≥≤≤-+-=++-⽆约束321321321,0,064..x x x kx x x x x x t s （1）(2)2-5运⽤对偶理论求解以下各问题：（1）已知线性规划问题：其最优解为（a ）求k 的值；（b ）写出并求出其对偶问题的最优解。

运筹学第二章线性规划

运筹学第二章线性规划

第二章线性规划教学目的和要求：目的：使学生具备线性规划的基本知识以及应用线性规划的基本能力。

要求：理解线性规划概念，标准型，解的概念，基本定理；掌握单纯形法，人工变量法，了解图解法。

重点：线性规划标准型，解的概念，单纯形法，人工变量法。

难点：线性规划基本定理，单纯形法。

教学方法：讲授法，习题法。

学时分配：12学时 作业安排：见教材P 38.线性规划是运筹学的一个重要分支。

1939年苏联科学家康托罗维奇提出了生产组织和计划中的线性规划模型。

1947年美国学者丹捷格(George B.Dantzig)提出了求解一般线性规划问题的方法。

此后，线性规划理论日趋成熟，应用也日益广泛和深入。

第一节线性规划问题一、问题的提出在企业的生产经营活动中经常会面临这样两类问题：一是如何合理地利用有限的人力、物力、财力等资源，取得最佳的经济效果；二是在取得一定的经济效果的前提下，如何合理安排使用人力、物力、财力等资源，使花费的成本最低。

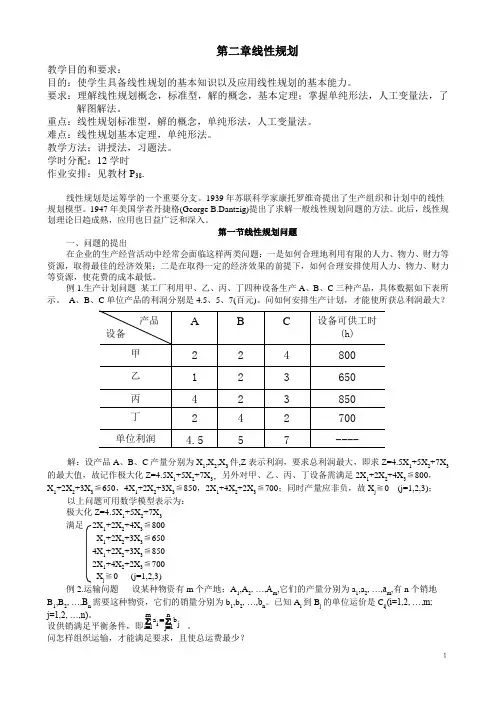
例1.生产计划问题 某工厂利用甲、乙、丙、丁四种设备生产A 、B 、C 三种产品，具体数据如下表所示。

A 、B 、C 单位产品的利润分别是4.5、5、7(百元)。

问如何安排生产计划，才能使所获总利润最大？解：设产品A 、B 、C 产量分别为X 1,X 2,X 3件,Z 表示利润，要求总利润最大，即求Z=4.5X 1+5X 2+7X 3的最大值，故记作极大化Z=4.5X 1+5X 2+7X 3，另外对甲、乙、丙、丁设备需满足2X 1+2X 2+4X 3≦800，X 1+2X 2+3X 3≦650，4X 1+2X 2+3X 3≦850，2X 1+4X 2+2X 3≦700；同时产量应非负，故X j ≧0 (j=1,2,3)；以上问题可用数学模型表示为： 极大化Z=4.5X 1+5X 2+7X 3 满足 2X 1+2X 2+4X 3≦800 X 1+2X 2+3X 3≦6504X 1+2X 2+3X 3≦850 2X 1+4X 2+2X 3≦700X j ≧0 (j=1,2,3)例2.运输问题 设某种物资有m 个产地；A 1,A 2, …,A m ,它们的产量分别为a 1,a 2, …,a m ,有n 个销地B 1,B 2, …,B n 需要这种物资，它们的销量分别为b 1,b 2, …,b n 。

管理运筹学第二章线性规划的图解法

管理运筹学第二章线性规划的图解法

02
图解法的基本原理
图解法的概念
图解法是一种通过图形来直观展示线性规划问题解的方法。它通过在坐标系中绘 制可行域和目标函数，帮助我们理解问题的结构和最优解的位置。
图解法适用于线性规划问题中变量和约束条件较少的情况，能够直观地展示出最 优解的几何意义。
图解法的步骤
确定决策变量和目标函数
明确问题的决策变量和目标函数，以便在图 形中表示。
目标函数是要求最小化或最大化的函数，通常表示为 $f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
04
约束条件是限制决策变量取值的条件，通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
LINDO是一款开源的线性规划求解器，用 户可以免费使用。
软件工具的使用方法
Excel
用户需要先在Excel中设置好线性规划模型，然后使 用“数据”菜单中的“规划求解”功能进行求解。
Gurobi/CPLEX/LINDO
这些软件通常需要用户先在软件界面中输入线性规划 模型，然后通过点击“求解”按钮进行求解。
实例三：分配问题
总结词
分配问题是指如何根据一定的分配原则 或目标，将有限的资源分配给不同的需 求方，以最大化整体效益。
VS
详细描述
分配问题在实际生活中广泛存在，如物资 分配、任务分配等。通过图解法，可以将 分配问题转化为线性规划模型，并利用图 形直观地展示最优解的资源分配方案。在 分配问题中，通常需要考虑不同需求方的 重要性和优先级，以及资源的有限性等因 素，以实现整体效益的最大化。

管理运筹学_第二章_线性规划的图解法

管理运筹学_第二章_线性规划的图解法

线性规划中超过约束最低限的部分，称为剩余量。 记s1,s2为剩余变量，s3为松弛变量，则s1=0, s2=125,
s3=0，加入松弛变量与剩余变量后例2的数学模型变为 标准型： 目标函数： min f =2x1+3x2+0s1+0s2+0s3 约束条件： x1+x2-s1=350， x1-s2=125, 2x1+x2+s3=600, x1, x2, s1,s2,s3≥0.
阴影部分的每 一点都是这个线 性规划的可行解， 而此公共部分是 可行解的集合， 称为可行域。
B
X2=250
100
100
300
x1
B点为最优解， X1+X2=300 坐标为（50, 250）， Z=0=50x1+100x2 此时Z=27500。 Z=10000=50x1+100x2 问题的解： 最优生产方案是生产I产品50单位，生产Ⅱ产品250单位，可得 最大利润27500元。
Z=10000=50x1+50x2
线段BC上的所有点都代表了最优解，对应的最优值相 同： 50x1+50x2=15000。
10
3. 无界解，即无最优解的情况。对下述线性规划问题：
目标函数：max z =x1+x2 约束条件：x1 - x2≤1 -3x1+2x2≤6 x1≥0, x2≥0．
x2 -3x1+2x2=6 3
其中ci为第i个决策变量xi在目标函数中的系数， aij为第i个约束条件中第j个决策变量xj的系数， bj(≥0)为第j个约束条件中的常数项。
16
灵敏度分析
灵敏度分析：求得最优解之后，研究线性规划的

运筹学02-线性规划的图解法

运筹学02-线性规划的图解法
10
s.t
约束条件
(2) 线性规划模型标准形式
价值系数
Max
技术系数
Z c1 x1 c2 x2 cn xn a11 x1 a12 x2 a1n xn b1 a21 x1 a22 x2 a2 n xn b2 a x a x a x b mn n m m1 1 m 2 2 x1 , x2 ,, xn 0 b1,b2 , ,bm 0

若线性规划问题有可行解，但无有限最优解，则可 行域必然是无界的； 若线性规划问题无可行解，则可行域必为空集。

9
2.3 线性规划问题的标准形式
(1) 线性规划模型一般形式
目标函数
MaxMin
Z c1 x1 c2 x2 cn xn a11 x1 a12 x2 a1n xn , b1 a x a x a x , b 21 1 22 2 2n n 2 a x a x a x , b mn n m m1 1 m 2 2 x1 , x2 , , xn 0
27
2.4.2 约束条件中右边系数 bj 的灵敏度分析
当约束条件中右边系数 bj 变化时，线性规划的可行域发生 变化，可能引起最优解的变化。 考虑例1的情况： 假设设备台时增加10个台时，即 b1变化为310，这时可行 域扩大，最优解为 60，x2 = 250 。 变化后的总利润 - 变化前的总利润 = 增加的利润 (50×60+ 100×250) - (50 × 50+100 × 250) = 500 ， x2 = 250 和 x1 + x2 = 310 的交点 x1 =

运筹学第2章-线性规划的对偶理论

运筹学第2章-线性规划的对偶理论
❖ 影子价格不是市场价格，而是在现有技术和管理条件下， 新增单位资源所能够创造的价值，是特定企业的一种边 际价格；不同企业或同一企业不同时期，同种资源的影 子价格可能不同；当市场价格高于影子价格，可以卖出； 相反，则应买进，以获取更大收益
Ma例x：Z （ 2第x一1 章3例x22）
2 x1 2 x2 12
当原问题和对偶问题都取得最优解时，这 一对线性规划对应的目标函数值是相等的：
Zmax=Wmin
二、原问题和对偶问题的关系
1、对称形式的对偶关系
（1）定义：若原问题是
MaxZ c1 x1 c2 x2 cn xn
a11x1 a12 x2 a1n xn b1
s.t.a21
x1
a22
二、 手工进行灵敏度分析的基本原则 1、在最优表格的基础上进行； 2、尽量减少附加计算工作量；
5y3 3
，y
2
3
0
（用于生产第i种产 品的资源转让收益不 小于生产该种产品时 获得的利润）
对偶变量的经济意义可以解释为对工时及原材 料的单位定价 ；
若工厂自己不生产产品A、B和C，将现 有的工时及原材料转而接受外来加工时， 那么上述的价格系统能保证不亏本又最富 有竞争力（包工及原材料的总价格最低）
内，使得产品的总利润最大 。
MaxZ 2x1 3x 2
2x1 2x2 12
s.t.54xx12
16 15
x1, x 2 0
它的对偶问题就是一个价格系统，使在平衡了 劳动力和原材料的直接成本后，所确定的价格系统 最具有竞争力：
MinW 12y1 16y2 15y3
2y1 4y2
2
s.t.2y1y，1y
y1, y2, , ym 0

运筹学—线性规划第2章

运筹学—线性规划第2章

1 1
1 0
0 1
0 0
6 2 0 0 1
1 0 0
则
B 0
1
0
的列是线性无关的，即
1
0
0 0 1
p3 0, p4 1 0 0
•
0
p5 0 是线性无关，因此 1
x3
x4
x5
是, 0
p2
1 2
不在这个基中，所以x1,
x2为非基变量。
定义10：使目标函数达到最优值的基本可行解，称为基
本最优值。
• 例4：（SLP)如例3，试找一个基本可行解。
1 1 0
解：B1
1
0
0
是其一个基矩阵.p1,p3, p5是一个基。
6 0 1
则 x1 , x3, x5为基变量。X2, x4为非基变量。令 x2=x4=0. 得x1=2, x3=3, x5=9. 故 x1=(2,0,3,0,9)是原问题的一个基本 可行解，B1为基可行基。
•当 由0连续变动到1时，点z由y沿此直线连续的变动到x，且 因z-y平行x-y，则有：z y (x y) 于是有：
z x (1 ) y
•这说明当 0 1 时，x (1 ) y表示以x.y为端点的直线段
上的所有点，因而它代表以 x.y为端点的直线段。 一般地，如果x.y是n维欧氏空间Rn中的两点，则有如下定义：
• 定义14：设R是Rn中的一个点集，（即R Rn），对于任意 两点x R, y R 以及满足0 1 的实数 ,恒有
x (1 )y R
则称R为凸集。
• 根据以上定义12及13可以看到，凸集的几何意义是：连接凸 集中任意两点的直线段仍在此集合内。
其可行域如上图，可行解（3，1，0，0）T。用x1, x2 表示则为图上点（3，1）。由图可见这不是可行域的 顶点。而我们将证明基本可行解是可行域的顶点。而 在例4中p1,p3线性无关，所以B=(p1,p3)是一个基矩阵， 对应的基本解为（4，0，0，0）T。用坐标x1, x2表示则 为平面上的点（4，0），是上图可行域的顶点。

《运筹学教学课件》第二章 线性规划应用举例

《运筹学教学课件》第二章 线性规划应用举例
备的费用如下表，要求安排最优的生产计划，使该厂利润最大。
2.21 某公司在第一年有 100 万元资金。每年 都有以下的投资方案可供考虑采纳：“假如 今年投入一笔资金，明年又继续投入此资金 的 50%，那么到后年就可收回今年初投入资 金的两倍金额。”该公司要如何决定最优投 资策略才可使第六年拥有的资金最多。
上机求解的结果是：
即每天用475公斤原料A，725公斤原料B，500公斤原料C，800 公斤原料D来生产2500公斤产品1；以及用525公斤原料A，275 公斤原料B，250公斤原料C来生产1 050公斤产品2，可获得最大 利润为13825元。
例15（多阶段投资问题） 某公司有100万元用于投资，可选择的投资项目如下所示： 项目A：从第一年到第四年每年年初都可投资，并于次年末回 收本利110%，规定每年的最低投资额为10万元； 项目B：第二年初可以投资，到第五年年末能收回本利135%， 规定投资额不超过20万元； 项目C：第三年初可以投资，到第五年末回收本利125%，规定 最低投资额为20万元，最高投资额为40万元； 项目D：五年内每年初都可投资，年末回收本利104%。 问该公司应如何确定给这些项目每年的投资额，使到第五年末 回收资金的本利总额为最大？
到第五年末该公司回收资金的本利总额为132.88（万元），即盈利32.88%。
本例的另一个最优解（单位：万元）为：
例18（餐巾供应问题） 某饭店筵席部预计一周每天接待的客人数如下表所示：
规定每位客人每天用餐巾一条。所用餐巾中可购买新的，每条成本6元，或 用已经洗净的餐巾。附近有两家洗衣店：甲店洗净一条餐巾收费3元，隔一天后 送还；乙店洗净一条收费2元，隔两天后送还。假定第7天后餐巾应换新的，且每 周开始时没有旧餐巾。问饭店后勤部应如何安排各天餐巾的供应，以使总成本最 低？

chapter2线性规划

chapter2线性规划

二.线性规划问题的图解法
1.图解法求最大化的步骤：
第一步，得到可行域，也就是满足所有约束条
件的自变量组成的集合。 第二步，在可行域中找到使目标函数最大的那 一点，也就是最优解。 第三步，通过最优解，求出目标函数的最优值。
案例：考虑生产规划模型：
max z 50 x1 100 x 2 x1 x 2 300 2 x x 400 1 2 x 2 250 x1 , x 2 0
注3:
一般优化模型的基本类型： (1)只有目标函数而没有约束条件和非负约束 的特殊情况称为无约束规划. (2)当模型中的决策变量取值为连续数值(实 数)时,称为连续优化即通常所说的数学规划; 此时,如果目标函数与约束条件都是线性函数, 成为线性规划(linear programming,LP).至少 有一个是非线性函数,则称为非线性规划 (nolinear programming,NLP).特别当目标函数 为二次函数,而约束条件为线性函数,称为二 次规划(quadratic programming,QP).
件中含有变量的非线性的等式或不等式的数学
模型称之为非线性规划。
(2)线性规划的目标函数为线性函数：z=ax，x 为自变量，a为参数。当a>0时，z随着x的增加 而增加，无论x为多少，x增加一个单位带来的z 的增加总是同样的a。 由于其性质，没有约束条件的时候max z=ax是 不存在的，趋向于无穷大，所以现实的模型必 须包括对自变量取值的限制，例如加入 0<=x<=5。
max z 50 x1 100 x 2 x1 x 2 300 2 x x 400 1 2 x 2 250 x1 , x 2 0

运筹学第四版第二章线性规划及单纯形法

运筹学第四版第二章线性规划及单纯形法

方案的制定受到那些现实条件制约：
确定约束条件
人力资源（劳动力）的限制： 9x1 4x2 360
设备工时的限制：
4x1 5x2 200
原材料资源的限制：
3x1 10x2 300
此外，决策变量的取值不应为负值即 x1 0, x2 0
6
综上所述，我们得到了这个问题的数学模型
目标函数 约束条件
大？
项目
Ⅰ
设备A (h)
0
设备B (h)
6
调试工序(h) 1
利润（元） 2
Ⅱ 每天可用能力
5
15
2
24
表1-2
1
5
1
12
其数学模型为：
max Z 2x1 x2
5x2 15
6xx11
2x2 x2
24 5
x1, x2 0
13
例3：捷运公司在下一年度的1～4月份的4个月内拟租用仓库
堆放物资。已知各月份所需仓库面积列于下表1-3。仓库租
借费用随合同期而定，期限越长，折扣越大，具体数字见表
1-4。租借仓库的合同每月初都可办理，每份合同具体规定
租用面积和期限。因此该厂可根据需要，在任何一个月初办
理租借合同。每次办理时可签一份合同，也可签若干份租用
面积和租用期限不同的合同。试确定该公司签订租借合同的
最优决策，目的是使所租借费用最少。
14
max Z 70 x1 120 x2
9x1 s.t. 43xx11
x1,
4x2 5x2 10x2 x2 0
360 200 300
资源约束
非负约束
其中 约束条件可记 s.t (subject to), 意思为“以… 为条件“、”假定“、”满足“之意。

运筹学第二章——第八节—线性规划的对偶理论

运筹学第二章——第八节—线性规划的对偶理论

四、对偶问题经济学含义——影子价格
因为Z*=Y*=Yb 所以：Δ Z/ Δ b=Y b——资源的量 Z——目标函数 经济学含义：资源每变动一个单位，目标函 数（利润、总产值等）变动的大小。 资源对生产做出的贡献。（影子价格） 是对现有资源实现最大效益的一个评价，叫 机会成本。
V*X=0， Y*U=0，其中V是对偶问题的剩余变量，U是 原问题的松弛变量。
（七）原问题在单纯性法迭代过程中的检验 数对应于对偶问题的一个基本解。（对应性 定理） 原问题 XB XN 对应基B检验数 0 CN-CBB-1BN 对偶问题的变量 -YS1 -YS2 XS –CBB-1 -Y
对偶问题性质的启示
原问题 有最优解 无可行解 有可行解无上界 无有限最优解 对偶问题 有最优解 无可行解 无有限最优解 有可行解但无下界
由互补松弛性定理可知： 当U>0，即AX <b时，资源未充分利用时，影 子价格为0。
二、原问题与对偶问题之间的转化
1、目标函数 MAX——Min 2、约束条件——变量 约束条件n个——变量n个 约束条件≥0 ——变量≤ 0 约束条件≤ 0 ——变量 ≥ 0 约束条件=0——变量无约束 要点：max为反向关系（约束条件——变量）
二、原问题与对偶问题之间的转化
3、变量——约束条件 变量m个——约束条件m个 变量≥0——约束条件≥ 0 变量≤ 0 ——约束条件≤ 0 变量无约束——约束条件=0 4、目标函数中变量的系数C为对偶问题中约 束条件的右端常数项b，个数对等变动。
（五）若原问题和对偶问题具有可行解，若 原问题或对偶问题之一有最优解，则另一个 对偶问题也必有最优解，且最优值相同。 （主对偶性定理） 证明 含义： 若原问题有一个对应于基B的最优解，则 CBB-1为对偶问题的最优解。

运筹学第二章第6节矩阵法求解线性规划问题

运筹学第二章第6节矩阵法求解线性规划问题

B N1 ; 其中 B N B S2
;
X S1 X S2
基变量 非基变量
目标函数
max z C B X CB X
B B
CN X C N1 X
N N1
C S2 X S2
N1
(1)
约束条件
BX b
B
2 x1 [1] 4 0 2
3 x2 0 0 1 0
0 x3 1 0 0 0
0 x4 0 1 0 0
0 x5 0 1/4 -3/4 θ 4 -
-1/2 2
在迭代到单纯性表2时，当前的基变量为x3，x4，x2，其中 x3和x4是松弛变量。这时，松弛变量中，x5为基变量，x3和 x4为非基变量，因此：基变量XB由两部分组成，一部分是 XB1=x2，一部分是XS1=x3和x4；非基变量XN由两部分组成， 一部分是XN1=x1，另外一部分是XS2=x5。
第七节 矩阵法求解线性规划问题
一、线性规划问题的矩阵描述 二、矩阵法求解线性规划问题 （改进的单纯性法）
一、线性规划问题的矩阵表示
线性规划问题可以用如下矩阵形式表示： 目标函数 max z=CX 约束条件 AX≤b 非负条件 X≥0 将该线性规划问题的约束条件加入松弛变量后，得到标 准型：其中I 是m×m单位矩阵。
1 0 2 1/ 2 1/ 4 1/ 4 1/ 2 1/8
=(0,0)-(3/2,1/8)=(-3/2,-1/8)
2)Z=CBB-1b=CBXB =14 1 1
0 ( 0 , 2 , 0 ,3 ) 0 0 0 2 1/ 2
1/ 4 1/ 4 1/ 2 1/8
0 0 1 0
12 8 16 12

第二章 运筹学

第二章 运筹学

提出问题:
•当线性规划问题的系数有一个或几个发生变化时，已求得 的最优解会有什么变化； •这些系数在什么范围内变化时，线性规划问题的最优解不 会变化。
灵敏度分析的内容
再看线性规划模型： Max Z = 300x1+ 500x2 x1 ≤4 （车间1） （车间2） （车间3） （非负）
s.t.
2 x2 ≤12
Row 2 3
Righthand Side Ranges Current Allowable Allowable RHS Increase Decrease 30000.00 10000.00 20000.00 100.0000 200.0000 25.00000
练习二 1. 某工厂利用原材料甲、乙、丙生产产品 A，B，C。问：
“DUAL PRICE”（对偶价格，即影子价格）输出结果中对应 于每一个约束有一个对偶价格。 表示对应约束中不等式右端 项若增加 1 个单位，目标值将增加的数量（max型问题）。 如：车间2：12→13，总利润变化量 = 影子价格 = 150 元； 车间3：18→17，总利润变化量 = - 影子价格 = - 100 元
Ranges in which the basis is unchanged:
Objective Coefficient Current Allowable Variable Coefficient Increase X1 1.000000 0.2500000 X2 2.000000 2.000000 X3 3.000000 0.3333333 Ranges Allowable Decrease 0.5000000 0.1428571 INFINITY
2 x2 6
可行域 （利润） z 300 4 500 3 2700
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

量分别为：x1、x2 、x3 、x4
2.目标函数：设总成本为z
min z = 5 x1 + 6 x2 + 7 x3 + 8 x4 3.约束条件：
x1 + 2x2 + x3 + x4 ≥160
要求：生产A种药物至少160 单位；B种药物恰好200单位， C种药物不超过180单位，且 使201原9/5/料14 总成本最小。
x1 0 xn 0
n
简写为： max(min) Z c j x j j1
n
aij x j ( ) bi (i 1 2m)
j1
xj 0
(j 1 2n)
2019/5/14
12
线性规划问题的数学模型
向量形式： max (min)z CX

2019/5/14
10
4. 建模步骤
线性规划问题的数学模型
(1) 确定决策变量：即需要我们作出决策或选择的量。一般 情况下，题目问什么就设什么为决策变量；
(2) 找出所有限定条件：即决策变量受到的所有的约束；
(3) 写出目标函数：即问题所要达到的目标，并明确是max 还是 min。
2019/5/14
解： 设：xj为第j号类型船队的队数（j = 1，2，3，4），
z 为总货运成本 则： min z = 36x1 + 36x2 + 72x3 + 27x4
x1 + x2 + 2x3 + x4 ≤ 30
2x1
+ 2x3
≤ 34
4x2 + 4x3 + 4x4 ≤ 52
25x1+20x2
＝200
40x3+20x4 ＝400
xj ≥ 0 （ j = 1,2,3,4）
2019/5/14
8
2. 线性规划的数学线模性型规由三划个问要题素的构数成学模型
决策变量 Decision variables 目标函数 Objective function 约束条件 Constraints
怎样辨别一个模型是线性规划模型？ 其特征是： （1）问题的目标函数是多个决策变量的线性函数， 通常是求最大值或最小值； （2）问题的约束条件是一组多个决策变量的线性不 等式或等式。
2x1
+4 x3 +2 x4 ＝200
3x1 ＋x2 +x3 +2 x4 ≤180
x1、x2 、x3 、x4 ≥0
6
线性规划问题的数学模型
例1.5 某航运局现有船只种类、数量以及计划期内各条航线 的货运量、货运成本如下表所示：
航线号
船队 类型
1 1
2
3 2
4
拖轮
1 1 2 1
编队形式 A型 驳船 2 — 2 —
Chapter2 线性规划及单纯形法
(Linear Programming)
本章主要内容：
LP的数学模型 图解法 单纯形法 单纯形法的进一步讨论－人工变量法 LP模型的应用
2019/5/14
1
• 1. 规划问题
线性规划问题的数学模型
生产和经营管理中经常提出如何合理安排，使人力、
物力等各种资源得到充分利用，获得最大的效益，
2019/5/14
9
3. 建模条件
线性规划问题的数学模型
(1) 优化条件：问题所要达到的目标能用线型函数描述，且 能够用极值（max 或 min）来表示；
(2) 限定条件：达到目标受到一定的限制，且这些限制能够 用决策变量的线性等式或线性不等式表示；
(3) 选择条件：有多种可选择的方案供决策者选择，以便找 出最优方案。
能使总利润最大？
x1， x2≥0
2019/5/14
4
线性规划问题的数学模型
例1.3 已知资料如下表所示， 问如何安排生产才能使利润 最大？
设备
产品
AB C
Ⅰ
214
利润
D （元）
02
Ⅱ
220 4 3
有 效 台 时 12 8 16 12
解：
1.决策变量：设产品I、II的产量分
别为 x1、x2
2.目标函数：设总利润为z，则 有： max z = 2 x1 + 3x2
B型 驳船 —
4 4 4
货运成本 （千元／队）
36 36 72 27
货运量 （千吨）
25 20 40 20
船只种类 拖轮 A型驳船 B型驳船
船只数
30 34 52
航线号
1 2
合同货运量
200 400
问：应如何编队，才能既完成合同任务，又使总货运成本为最小？
2019/5/147线性规划问题的数来自模型分别为 x1、x2
项目
Ⅰ Ⅱ 每天可用能力
2.目标函数：设总利润为z，则有：
设备 A（h） 0
5
15
设备 B（h） 6
2
24
调试工序（h） 1
1
5
利润（元） 2
1
问：应如何安排生产计划，才
max z = 2 x1 + x2 3.约束条件：
5x2 ≤ 15 6x1+ 2x2 ≤ 24 x1+ x2 ≤ 5
这就是规划问题。
线性规划通常解决下列两类问题：
（1）当任务或目标确定后，如何统筹兼顾，合理安排，用 最少的资源 （如资金、设备、原标材料、人工、时间等） 去完成确定的任务或目标
（2）在一定的资源条件限制下，如何组织安排生产获得最 好的经济效益（如产品量最多 、利润最大.）
2019/5/14
2
• 例1.1 如图所示，线如性何截规取划x使问铁皮题所的围数成的学容模积型最大？

pj xj

(
) B
X 0
其中： C (c1 c2 cn )
x
v a 2x2 x a dv 0 dx
2(a 2 x) x (2) (a 2 x)2 0 x a 6
2019/5/14
3
线性规划问题的数学模型
例1.2 某厂生产两种产品， 解：
下表给出了单位产品所需资 源及单位产品利润
1.决策变量：设产品I、II的产量
3.约束条件：
2x1 + 2x2 ≤ 12
x1 + 2x2 ≤ 8
4x1
≤ 16
4x2 ≤ 12 x1 ≥ 0 , x2 ≥ 0
2019/5/14
5
线性规划问题的数学模型
例1.4 某厂生产三种药物， 解：
这些药物可以从四种不同的 1.决策变量：设四种原料的使用
原料中提取。下表给出了单 位原料可提取的药物量
11
线性规划问题的数学模型
5. 线性规划数学模型的一般形式
目标函数： max (min) z c1 x1 c2 x2 cn xn
a11 x1 a12 x2 a1n xn ( ) b1
约束条件：




am1 x1 am2 x2 amn xn ( ) bm